A high-impedance detector-array glove for magnetic resonance imaging of the hand

Abstract

Densely packed resonant structures used for magnetic resonance imaging (MRI), such as nuclear magnetic resonance phased-array detectors, suffer from resonant inductive coupling, which restricts coil design to fixed geometries, imposes performance limitations, and narrows the scope of MRI experiments to motionless subjects. Here, we report the design of high-impedance detectors, and the fabrication and performance of a wearable detector array for MRI of the hand, that cloak themselves from electrodynamic interactions with neighboring elements. We experimentally verified that the detectors do not suffer from signal-to-noise degradation mechanisms typically observed with the use of traditional low-impedance elements. The detectors are adaptive and can accommodate movement, providing access to the imaging of soft-tissue biomechanics with unprecedented flexibility. The design of the wearable detector glove exemplifies the potential of high-impedance detectors in enabling a wide range of applications that are not well suited to traditional coil designs.

Founded on the principles of nuclear magnetic resonance (NMR)[1], magnetic resonance imaging (MRI)[2, 3] is a pre-eminent clinical imaging modality and invaluable research tool. The rich information sought after in the NMR experiment is locked away deep in the interaction of the nuclei with one another and with the applied external magnetic field. The key to extracting this information is the deliberate perturbation of nuclear spins, and careful tracking of their response – a sequential process reliant on radiofrequency (RF) magnetic fields, generated and observed by RF coils tuned to the Larmor frequency of the nuclear spins in question.

Modern-day magnetic resonance (MR) systems use phased array coils constructed out of low impedance resonant loops[4]. Inside such arrays, electrodynamic interactions between elements must be carefully balanced. Neighboring coil elements are strategically overlapped to minimize inductive coupling, and preamplifier interfaces are tuned to suppress the induced current on each element (Fig. 1a). This electromechanical balancing act becomes increasingly difficult as the number of receive elements grows to approach optimal performance[5, 6, 7, 8, 9, 10, 11], leading to geometrical puzzles of profound complexity[12, 13, 14]. Any change in coil structure disturbs the delicate balance, thus demanding rigid structures which retain the critical overlap, and which, therefore, cannot adapt to the variable needs of individual subjects, or provide the flexibility needed to study moving joints or other body kinematics.

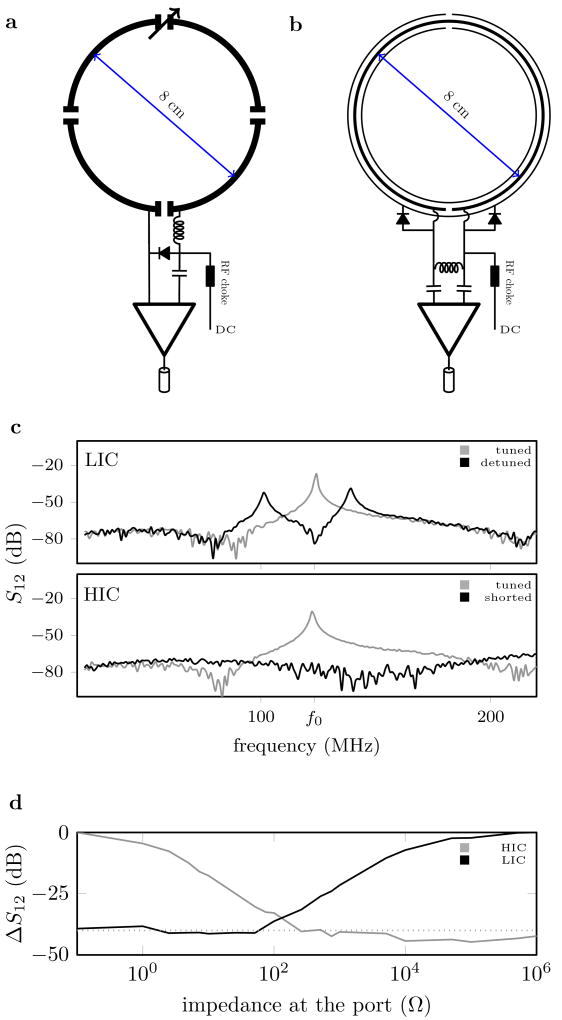
Fig. 1.

Schematic drawing of a traditional LIC (a) and HIC (b) element, along with plots of the resonances observed with a double probe experiment when the coil is tuned and detuned (c), and the relative amplitude (ΔS_1,2) of the induced current measured at the resonance frequency (f₀) during a double probe experiment as a function of the impedance at the port (d). Bench measurements were performed multiple times with similar results, one representative experiment shown.

Here we show that a high impedance coil (HIC) design can eliminate all electrodynamic interactions between receive elements in a phased array coil. First, we introduce the HIC design concept and characterize its properties. We then present an exemplary application, the wearable “glove coil”, which conforms to the shape of the hand, and enables the study of soft tissue mechanics as the hand moves freely inside the MR system, allowing us to see how the intricate arrangement of muscles and ligaments in the hand changes during complex tasks.

High-impedance NMR detector

The key function of inductive detectors is to measure the electromotive force (EMF) induced by the NMR signal. Traditional low impedance coils (LIC) efficiently capture the EMF, but also allow current to flow. This current, in turn, creates a secondary RF field that can be detected by neighboring elements. To eliminate resonant inductive coupling between elements we set out to develop a new element design, which allows the EMF to be measured without allowing current to flow and signal to leak inductively into neighboring elements.

Inspired by developments in wireless power transfer systems [15, 16], we designed a high impedance resonant coaxial NMR probe (Fig. 1b). In contrast to conventional LIC elements, there are no lumped capacitors to adjust the resonance frequency or distribute the current. Instead, our HICs were tuned by adjusting the length, the relative permittivity of the substrate, and the ratio between inner and outer conductor diameter[17], such that the Larmor frequency of interest coincides with the lowest resonance of the structure. In this situation, EM simulations (CST microwave studio, Darmstadt, Germany) reveal that the current on the inner conductor increases approximately linearly from zero at the gap to a maximum at the gap of the outer conductor, which is mirrored by an opposing current distribution on the inner surface of the outer conductor. At the gap in the outer conductor, skin depth effects allow a current to flow through the gap onto the outer surface of the conductive wrapping of the coil, and this current travels uniformly towards the other edge of the gap (Fig. S1). Shorting the gap in the inner conductor through the outer conductor precludes the formation of the appropriate mirror currents, eliminating all resonances across a broad spectrum (Fig. 1c), which allows the coil to be detuned with PIN diodes during excitation.

The same idea can be leveraged to suppress the current induced by the NMR phenomenon during signal reception. This suppression of currents represents a fundamental difference between LICs and HICs. To suppress the induced current, LIC elements require high impedance at the port, whereas a low impedance across the port is required in HIC elements (Fig. 1d). Consequently, implementing a “reverse preamplifier decoupling” scheme, which creates a low impedance at the port, suppresses all currents in a HIC arrangement, provided that the impedance at the port is significantly lower than the intrinsic impedance of the HIC itself (≈ 2kΩ). Whereas creating a sufficiently low impedance at the LIC port is possible only at one isolated frequency and requires precise fine tuning of the preamplifier interface, reversed preamplifier decoupling in a HIC arrangement suppresses all currents over a wide range of conditions.

A 3D printer (Fortus 360mc, Stratasys, Minnesota) was used to explore the design space of possible coaxial substrate configurations (Fig. S2). The lack of lumped elements [18, 19, 20], [21, 22, 23] in combination with the coaxial design [24] suggests that a high degree of mechanical flexibility may be possible with HIC coils. Given the possibility to make a more flexible coil in addition to leveraging the desirable decoupling properties of HICs, we settled on a 0.7 mm separation between the inner and outer conductor, the effective resolution limit of our printer for this type of structure, leading to a coil diameter of 8.0 cm when tuned to 123 MHz, the proton Larmor frequency of our 3 Tesla MRI scanner (Siemens, Erlangen, Germany). In addition to the data shown in Fig 1D, the high-impedance nature of the HIC elements can also be seen in the Smith charts showing S_1,1 vs frequency (Fig. S3).

High- vs low-impedance detectors

To evaluate how well HICs cloak themselves from one another, we placed three identical HIC elements side by side on top of a large conductive phantom (Fig. 2a). MR images were obtained with each coil individually (Fig. 2b), and also with all coils active simultaneously (Fig. 2c). For comparison, three conventional 8-cm-diameter LICs were constructed (Fig. 2d) and used for imaging under identical circumstances. When all coils are active at the same time, the signals measured using LICs are distorted due to coupling (Fig. 2 e vs f), whereas the receive profiles of the HICs remain unaltered (Fig. 2 b vs c).

Fig. 2.

Evaluation of signal coupling between three coil elements placed side by side. a) Three 8-cm diameter HIC elements. b) MR images obtained with each HIC individually in three separate measurements. c) Corresponding MR images obtained with all elements simultaneously active in one single measurement. d) Three 8 cm diameter LIC elements. e) MR images obtained with each LIC individually in three separate measurements. f) Corresponding MR images obtained with all LICs simultaneously active in one single measurement. All MR images are displayed on the same scale. Experiments have been repeated multiple times during separate sessions with similar results, one representative experiment shown.

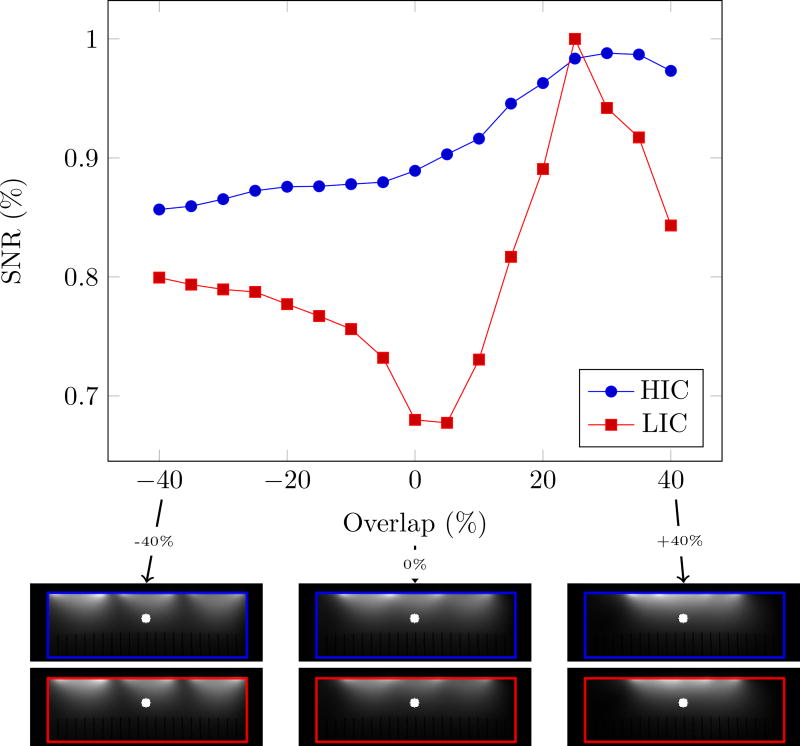
Although distinct coil-profiles are a key feature of the NMR phased array, crucial for parallel imaging[25, 26, 27] and modern multi-band techniques[28, 29], decoupling should not come at the expense of a reduced signal to noise ratio (SNR). To investigate this aspect, we evaluated the SNR at 4.2 cm (≈1/2 the coil diameter) depth below the center element as a function of coil overlap (Fig. 3). LIC elements reach their optimal performance when critically overlapped (≈25% of the diameter). When the outer coil elements are moved further apart or closer together, the SNR quickly deteriorates. The HIC elements, on the other hand, show almost no degradation in SNR as the overlap between them is changed (Fig. 3, blue curve). A similar analysis performed on a cylindrical surface is shown in supplemental figure 4.

Fig. 3.

Evaluation of SNR degradation due to coupling between neighboring coil elements as a function of coil overlap. The blue (HIC measurements) and red (LIC measurements) lines shows the SNR at 42mm below the center coil in a three-coil arrangement. The overlap between coils is varied between −40 and +40 %. The MR images below the graph show the combined signal images at −40, 0 and +40% overlap. The overlap was calculated based on the diameter of the loop. The blue (HIC data) and red (LIC data) outlines superimposed on the MR images mark the edges of the phantom. The white dot indicates the position of the SNR measurement. Experiments have been repeated 3 times during separate sessions with similar results, only the final (most refined) experiment is shown.

High-impedance detector-array glove

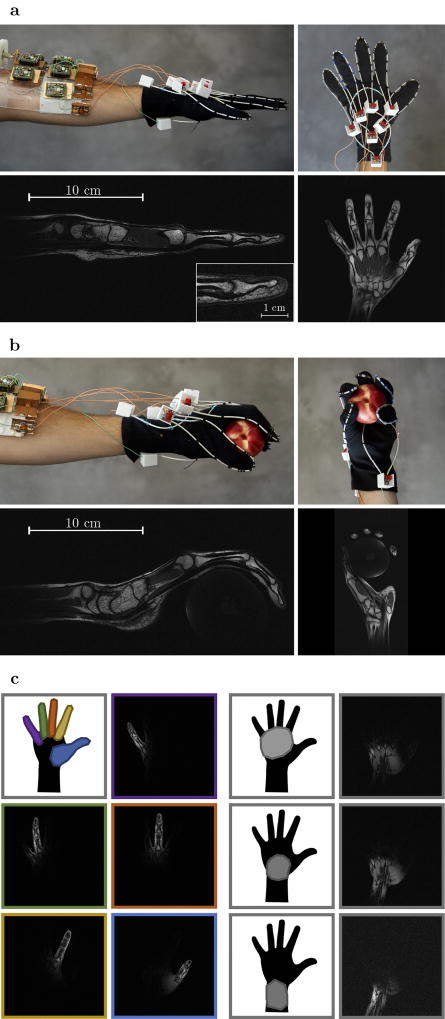
To illustrate the unique degrees of freedom provided by HIC elements, we created a wearable coil in the form of a glove (Fig. 4). In this proof of concept, eight HIC elements were stitched onto a cotton glove. The contours of each finger are traced by an individual coil, allowing all the joints in each finger to articulate freely. Two additional elements were stitched on the top of the hand and wrist, and one additional element was stitched on the bottom, allowing the carpal bones in the wrist joint to be studied as well.

Fig. 4.

Photos of the glove coil with the hand starched out and the corresponding T1 weighted MR images (a). Photos of the glove coil while holding a peach and the corresponding T1 weighted MR images (b). Illustrations showing where the individual coil elements are located on the hand next to the individual coil images obtained during a single T1 weighted measurement with all coils simultaneously activated (c). For a side by side comparison of simultaneously and sequentially acquired images see supplemental figure S5. The left hand of three volunteers was scanned during separate sessions, all experiments demonstrated similar image quality and flexibility. Images show representative results from one volunteer.

Figure 4a shows a coronal and sagittal slice through the hand, stretched out flat on top of the patient table. The close-fitting elements enable fast imaging with exquisite detail (250μm, 2mm slice). Although the coil elements on each finger are directly adjacent to one another in this configuration, distinct coil profiles are maintained (Fig. 4c and Fig. S5). One other unique feature of the glove array, where each individual element traces a distinct anatomical feature, is the ability to isolate individual fingers, simply by selecting the appropriate coil. Alternatively, a factor of 5 in acceleration can be achieved without g-factor penalty[26], by allowing all fingers to alias on top of one another, and relying purely on the coil signal isolation to directly reconstruct the individual images belonging to each finger (Fig. S6).

The flexibility of the HIC elements, combined with their immunity from electrodynamic coupling, enables the visualization of the intricate dynamics between ligaments, tendons and muscles during complex motions such playing piano/typing (Video S1), or grasping objects (Video S2). Thus, HIC elements open up new avenues for the study of complex joint motion, promising to facilitate, for example, the diagnosis, monitoring and treatment of repetitive strain injuries in athletes, musicians, and others.

Figure 4b shows the same hand in a different position, now holding a peach, to illustrate how the HIC elements conform to the shape of the hand. Because of the robustness to variations in coil overlap, the performance of the close-fitting coils remains unperturbed, allowing the study of intricate structures such as the pulley and flexor arrangement in different positions and even under load (Fig. S7). Although pulley ligaments and flexor tendon are almost indistinguishable based on underlying contrast (both have short T2 relaxation times), their interaction can now be examined by squeezing an object during the scan (Fig. S7), revealing how the pulley arrangement guides the flexor tendons and distributes the load. Additional high-resolution images (Fig. S8–9) can be found in the supplementary material.

It should be noted that, although the HIC design is extremely flexible and nearly immune to coupling effects, the inductance of the coil is still influenced by bending (Fig. S10). However, the extremely close fit of the glove coil, made possible in part by its flexibility and adjustability, creates a heavy loading condition, which helps to suppress these effects, thus allowing for a large range of motion.

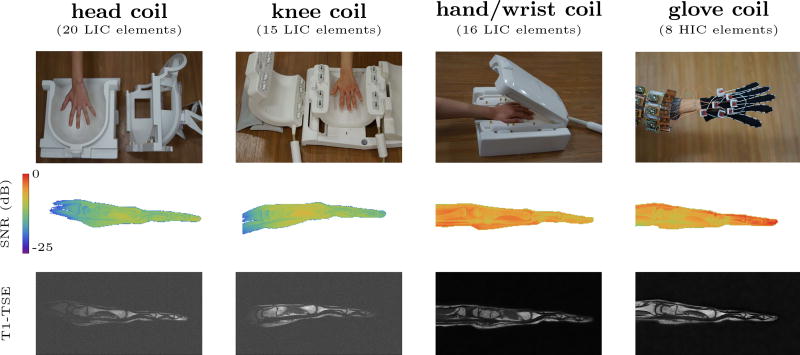
To put these results into perspective, we performed an in vivo evaluation of the SNR and flexibility provided by the glove coil compared to three state-of-the-art LIC phased arrays (Fig. 5). Each of these LIC coils enable a different range of motion. The close-fitting clamshell configuration of the traditional hand/wrist coil is designed to provide the highest possible SNR, but it precludes any form of motion. Alternatively, one may consider using a coil optimized for knee imaging. Such a coil can accommodate moderate wrist motion and finger flexing, at the cost of 3-fold SNR penalty (Table 1). If even more complex motions are to be studied using traditional designs one could opt for an even larger coil, such as a head array, at the price of an even larger SNR penalty. The HIC glove coil, on the other hand, provides complete freedom of motion while producing almost the same average SNR as the rigid stat-of-the-art hand/wrist coil, despite having only half the number of coil elements. Future iterations of the glove coil could benefit still further from additional elements on the palm of the hand, which is currently somewhat under-represented. In the current design, the philosophy behind the close-fitting, yet flexible, HIC elements are best captured by the finger elements on the glove, which demonstrated an 80% SNR improvement compared to the rigid close-fitting hand/wrist coil.

Fig. 5.

The performance of the HIC glove coil, compared to three state-of-the-art LIC phased arrays (20 element head coil, 15 element knee coil, and 16 element hand/wrist coil). The top row shows pictures of the coils. The middle row shows the SNR map (on a logarithmic scale). The bottom row shows a T1 weighted image obtained with each coil (250 μm in-plane, 2mm slice thickness). The 232 mm diameter head coil provides adequate space to perform complex motions such as grasping objects, but can only deliver 20% of the SNR provided by the dedicated hand/wrist coil. The smaller knee coil (154mm diameter), which only allows finger flexing and moderate wrist motion, can deliver about 29% of the SNR. The glove coil provides complete flexibility while providing SNR similar to that of the highly-optimized rigid hand/wrist coil (97%), despite using only half as many receive channels (see also Table 1). All in-vivo SNR measurements were performed once, during a single session with the same volunteer.

Table 1.

Quantitative SNR comparison.

	head coil (LIC)	knee coil (LIC)	hand/wrist coil (LIC)	glove coil (HIC)
hand + wrist	20%	29%	100%	97%
palm	22%	36%	103%	83%
fingertip	26%	15%	74%	188%

Average SNR in the hand and wrist, the fingertip, and the palm of the hand, compared to the state-of-the-art 16-channel LIC hand/wrist array.

Discussion

The proposed HIC elements also have a unique strength when deactivated. Multinuclear MR systems focusing on the less-abundant MR-visible nuclei rely on proton-based MR images to visualize the underlying anatomical structure, which requires the nesting of multiple RF coils operating at different frequencies[30, 31, 32, 33]. Whereas traditional LICs can only be detuned over a narrow bandwidth, leading to residual interactions that distort the RF fields and reduce the SNR, HIC elements detune across a wide range of frequencies (Fig. 1c).

High impedance coil elements may not be the only possible way to eliminate electrodynamic coupling between elements. General Electric (GE) recently demonstrated that a combination of specially engineered material (INCA wire) and so call “e-mode preamplifiers” may be able to achieve a similar effect [23]. The details of this technology, however, have not yet been disclosed. Besides any technical differences (to the extent that such differences can be understood based on currently available information), there is also a conceptual difference between our target high-impedance array designs and GE ”Air” coil arrays. Whereas the proof-of-principle blanket coil presented by GE aims to improve patient comfort and workflow in routine clinical practice [22], our glove coil is aimed at creating new avenues for the study, and diagnostic evaluation, of soft tissues in complex joined motion.

Over the years, several other designs have been proposed to eliminate lumped elements from the coil and enhance the mechanical flexibility [18, 19, 20, 21, 24]. The elegant printed coil design proposed by Corea et al [21], achieves a high degree of flexibility by printing conductive ink onto a flexible substrate. In this design, lumped elements are eliminated by layering different kinds of ink to produce the desired capacitance. This process enables flexible blanket-like coil arrays that may be draped over the abdomen or wrapped around an infant. In this case critical overlap between coil elements is maintained by the fixed relative coil locations on the sheet. Gonord [18], Serfaty [19], Frass-Kriegl [20], and Stensgaard [24], et al. have explored transmission line resonators that leverage the distributed capacitance of a dielectric substrate to eliminate lumped elements and enable the construction of flexible arrays [34, 35]. It may be possible to implement or adjust these designs to form flexible high impedance structures which could also benefit from the reversed preamplifier decoupling mechanism proposed here.

Traditional LIC elements come in many shapes and sizes. For example, a dense head coil array at 3 Tesla may use many loop-like elements with diameters as small as 55mm[36]. Cardiac coil arrays, on the other hand, may use rectangular elements as large as 330×270mm [37]. Here we used a circular loop diameter of 80mm for our phantom comparison. To create significantly smaller HIC elements, a thinner substrate (reduced r₁) or a substrate material with a higher relative permittivity must be used (Fig. S11). To create a very large HIC, however, would require an impractically thick substrate. For example, to create a HIC with a circumference comparable to the large rectangular loops used by Noeske et al [37], requires a substrate radius (r₁) of more than 10mm. Similarly, adaptation of the HIC design to other field strengths also requires different combinations of dimensions and dielectric materials (Fig. S11).

In addition to the above, skin depth effects may also need to be considered. In the HIC design, currents on the inner and outer surface of the outer conductor travel in opposite directions. At 123MHz, the skin depth in copper is ≈ 6μm. The coaxial wrappers used here are much thicker than 12μm and can easily support these opposing currents. At very low frequencies, however, this may become a problem. A more practical bottleneck, on the other hand, may be the thickness of the inner conductor. By definition, the inner conductor provides much less surface area to support current. Although a thinner inner conductor could result in HIC elements that are even more flexible, the additional losses may degrade the coil performance.

Outlook

The proposed HIC elements pave the way towards size-adjustable and flexible MR coils that allow greater patient comfort and facilitate new areas of research. For example, in addition to enabling the detailed non-invasive study of joint motion invivo and pushing the frontiers of multinuclear MR, HIC-based wearable MR coils can boost the study of brain development, by providing comfortable close-fitting high-density coil arrays that adapt to the subject size. In general, by freeing MR from the electromechanical constraints imposed by traditional low-impedance structures, HICs have the potential to bring MR to new areas with a premium on adaptability and a simultaneous need for the highest detector performance.

Methods

LIC construction

The conventional surface coils were constructed as loops 6mm in width and 80mm in diameter, routed out from a 31mil single-sided circuit board (Fig. 1a). Four capacitors were evenly distributed on each loop: two fixed 56pF capacitors (Series 11, Voltronics Corp., Denville, NJ) on either side, a variable capacitor on top for tuning, and an 82pF fixed capacitor for matching at the port. In addition to transforming the impedance of the coil to the optimal noise matching impedance of the preamplifier (Siemens Erlangen, Germany), the 82pF capacitor also forms a detuning trap with a positive-intrinsic-negative (PIN) diode (MA4P4002B-402; Macom, Lowell, MA, USA). The inductor in the trap was hand-wound. The coils were connected to low input impedance preamplifiers (Siemens Medical Solutions, Erlangen, Germany). The length of the cable connecting the coil and the preamplifier (24cm) was carefully adjusted to provide preamplifier decoupling.

HIC construction

The resonance frequency (f₀ = ω₀/(2π)) of the HIC elements was tuned by adjusting the length of the loops (2πr₀), the relative permittivity of the substrate (ε_r), and the ratio between the radius of the outer (r₁) and inner radius r₂ conductor (Supplemental figure 2 and 11).

The admittance as a function of angular frequency (Y (ω)) can be evaluated numerically by estimating the inductive and capacitive impedance of the HIC element. When tuned, i.e., open at the port, we may think of the HIC element as two open ended coaxial stubs of length l connected in series by the center conductor. In this case each arm adds a capacitive impedance (Z_c)

$$Z_C(\omega )=-i{Z}_0\mathit{\text{cot}}(\omega l\sqrt{{\epsilon }_r}/c)$$ (1)

where Z₀ the characteristic impedance of the coaxial line.

For a co-axial cylindrical conductor, the characteristic impedance is given by

$$Z_0(\omega )=\sqrt{\frac{R+i\omega L_{\mathit{\text{coax}}}}{G+i\omega C_{\mathit{\text{coax}}}}}$$ (2)

where R is the resistance per unit length, G is the conductance per unit length of the dielectric, L_coax is the inductance per unit length, and C_coax is the inductance per unit length. Assuming, R = 0 and G = 0, we find $Z_0=\frac{1}{2\pi }\sqrt{\frac{{\mu }_0}{{\epsilon }_0{\epsilon }_r}}\mathit{\text{ln}}(\frac{r_1}{r_2})$, where μ₀ is the permeability of free space.

The inductive impedance of the HIC can be approximated by the self inductance of the loop of similar size

$$Z_L(\omega )=i\omega {\mu }_0{r}_0(\mathit{\text{ln}}(\frac{8r_0}{r_1})-2).$$ (3)

Consequently, the admittance (Y_tuned = 1/Z) of the HIC can be approximated by

$$Y(\omega )={(Z_L(\omega )+2Z_C(\omega ))}^{-1}$$ (4)

where the factor 2 accounts for the two open ended stubs in the coil.

The above equations can be used to numerically explore the design space of possible HIC elements (see simulations section). The high impedance nature of this design is more clearly revealed by its equivalent circuit (a parallel resonator):

$$Z_{\mathit{\text{HIC}}}(\omega )=\frac{2Z_C(\omega )(R+Z_L(\omega ))}{R+Z_L(\omega )+2Z_C(\omega )}$$ (5)

where R = R_coil + R_load. If we now assume that the coil is unloaded (R_load = 0), i.e., that no phantom or subject is in range, and that the coil losses can be neglected (R_coil = 0), we find

$$\underset{\omega \to {\omega }_0}{\text{lim}}{Z}_{\mathit{\text{HIC}}}(\omega )=\infty$$ (6)

because Z_L(ω)+2Z_C(ω) tends to 0 as ω approaches the resonance frequency. In practice R may be in the order of 10Ω, which leads to the observed finite but high input impedance of approximately 2kΩ.

Computer-aided design of the coil substrate was performed in Solidworks (Dassault Systems, USA). The substrate was printed on a Fortus 360mc 3D printer (Stratasys, US) using polycarbonate, with a relative permittivity of ε_r = 2.2. The substrate for each coil was printed in two parts. The inner conductor was made from hand-wound copper threads (13 strands, final thickness 1mm) and the conductive mesh was taken from a commercial coaxial cable (RG58). First, the inner conductor was placed in the central grove of the substrate. The structure was then capped by adding the second half on top. The coaxial braid was placed around the substrate and stretched out to form a tight coaxial enclosure, taking care that the two halves of the dielectric properly encased the central conductor. Heat shrink tubing around the coaxial structure was used to insulate and protect the main structure. The radius (r₀) of the completed HIC loop was 40mm, the radius of the cylindrical inner conductor (r₂) was 0.5mm, the substrate thickness was 0.7mm and the diameter of the coaxial structure before shrink-wrapping was about 2.4mm (r₁ = 1.2mm). See also supplemental Figure 2.

The coil was then mounted on a 0.062mil single-sided circuit board (10mm×18mm) made with the same circuit router used to create the LICs described above. The two ends of the outer conductor were connected through the board, and a LC circuit was connected to the two ends of the inner conductor to transform the high impedance of the coil to the optimal noise matching of the preamp (Fig. 1b). The cable length connecting the coil and preamplifier (22cm) was adjusted to create a low impedance at the port. Here, we define the port as the two leads attached to the inner conductor of the coil. The combined circuit formed by the interface board, pre-amplifier and connecting cables effectively creates a short between the two ends of the inner conductor. Note that this is the exact opposite of preamplifier decoupling in traditional low impedance coils, for which a high impedance is arranged at the port. A detailed picture of the interface board can be found in the supplemental material (Fig S12).

Interestingly, the above-mentioned impedance transformation can be eliminated when using a high impedance metal-oxide-semiconductor field-effect transistor (MOSFET). Gallium Arsenide MOSFETs, for example, have an optimal noise figure at about 1 to 2 kΩ (similar to the intrinsic impedance of our HICs). Although removing the transformation network could help to further improve the SNR obtained using the proposed HIC design, we chose to use the same preamplifiers for both LIC and HIC coils to avoid any possible bias due to variations in the preamplifier design.

To detune the coil during transmit, two PIN diodes ware placed between the leads on the inner conductor and outer. When a direct current (DC) is provided, the PIN diodes short the two ends of the inner conductor to the outer conductor (forward bias). During receive, the stray capacitance of the PIN diode is incorporated into the matching network.

In addition to the 3D printed design, a HIC was also implemented using commercially available coaxial cable. RG178 was selected: a 50 cable with dimensions similar to the 3D printed coil design. The RG178 HIC was molded into the same shape as the 3D printed HIC by strapping it to a thin plastic sheet. The same interface, preamplifier and detuning configuration was used.

When building the HIC elements, one can make use of two mechanisms to adjust for imperfections and variations in the material specifications. Firstly, it is advisable to cut/print the coaxial stubs slightly longer than is nominally needed, so that they can be cut to size on the bench. Alternatively, it is also possible to include a tuning mechanism on the interface board. When the dimensions of the HIC are exactly right, the inductance and distributed capacitance cancel each other. In this situation, the impedance of the coil has no imaginary part. When the coil is too long, a capacitive imaginary component appears, which can be compensated by an inductor parallel to the residual capacitance. Similarly, when the coil is too short, an inductive imaginary component appears, which can be compensated with a capacitor parallel to the residual inductance.

Simulations

To visualize the current distribution on the HIC element (8 cm diameter), the coil was modeled in CST Microwave Studio (Darmstadt, Germany). Leveraging the reciprocity relation between transmit and receive fields, the coil was driven using a high impedance voltage source at the port (input power 0.5W). The preamplifier and detuning circuit were excluded from the simulation. The coil was placed 5mm above large cuboid phantom (317×317×104mm, σ = 0.53). Radiative boundary conditions were placed at a 100mm distance from the phantom and coil arrangement. The surface current density distributions were exported and analyzed in Mathematica (Wolfram Research, Champaign, IL). In addition, an 8 cm diameter LIC, driven using a low impedance voltage source at the port (input power 0.5W), was also simulated. For comparison, the |E| and $\left|B_1^{+}\right|$ are shown in supplemental figure 13.

In addition, Eq. 4. was used to numerically evaluate the landscape of possible coil sizes for use in a Proton MRI setup operating at 1.5, 3.0 and 7.0 Tesla (Fig S11). The Matlab code used to evaluate the coil dimensions is available at https://bitbucket.org/macloos/hic/wiki/Home. Similarly, the sensitivity of the resonance frequency to variations in material properties and design parameters were evaluated (Fig S14).

Bench experiments

A homemade double probe was attached to a network analyzer (Agilent, model E5071C) and the overlap was adjusted to eliminate mutual coupling (less than −70dB). To provide a baseline, the coupling between the two elements in the double probe (S_1,2) was measured in free space far from any object, over a frequency range of 20MHz to 200MHz. Subsequently, a LIC element was placed underneath the double probe, and the S_1,2 was measured in the tuned and detuned states. The same process was repeated using a HIC element.

To characterize how the impedance at the port influences the traditional current suppression mechanism of preamplifier decoupling for LICs and the proposed reversed preamplifier decoupling for HICs, a variable resistor was placed across the port of the coil, and the S_1,2 was measured using the double probe setup. The S_1,2 was recorded at the Proton Larmor frequency of interest (123MHz), and was plotted as a function of impedance at the port (Fig. 1d). In addition, we measured the S_1,1 of both HIC and LIC coils and plotted the Smith-Charts (Fig. S3).

Phantom experiments

To evaluate the interaction between coils and its effect on the SNR, a large cuboid phantom (317×317×104mm) was constructed. The phantom was filled with distilled water, doped with 2.5g/L Sodium chloride (NaCl, Sigma-Aldrich, St Louis, MO, USA) and 50 mg/L manganese (II) chloride tetrahydrate (Cl2Mn 4H20, Sigma-Aldrich, St Louis, MO, USA). The conductivity of the liquid was measured using an Agilent dielectric probe (model 85070E) attached to a network analyzer (model E5071C) calibrated using an eCal module (model 85093C). The conductivity was found to be 0.53 S/m.

Before the SNR experiments, the losses in the coil interface and receive chain were evaluated. A single LIC reference coil was placed on the center of the phantom and connected to the first port on the coil interface. Two gradient recalled echo (GRE) images, axially through the center coil, were acquired, one signal image (flip angle = 25 degrees) and one noise image (flip angle = 0 degrees). Sequence parameters were as follows: 3ms echo time, 200ms repetition time, 256×256 matrix, 384×384mm field of view, 5mm slice thickness, and 300 Hz/pixel readout bandwidth. These measurements were performed for each port on the interface (without moving the coil or interface). The relative signal to noise ratio between receive channels was calculated and incorporated into the subsequent SNR analysis.

Three series of experiments were performed. The first series of experiments was designed to show the effect of signal coupling between elements during receive. Three identical LICs were placed side by side on top of the phantom (≈5mm apart). Four GRE images were acquired: one using all three loops simultaneously, and one for each coil element individually with the other coil elements detuned (same sequence parameters described above). The same experiment was repeated using 3 HICs placed side by side (≈5mm apart). The same axial slice through the center of all three loops was used throughout the experiment.

The second series of experiments was designed to quantify the effect of coil overlap on the SNR. Again, three LIC elements were placed side by side, and this time the overlap between coil elements was varied between −40% and +40%, in increments of 5%, without moving the center element. The % overlap was calculated based on the diameter of the coil element. For example, a 25% overlap corresponds to a 12cm center-to-center distance between neighboring elements. For each overlap, two gradient echo images were acquired using all three loops simultaneously (same sequence parameters as before), once using a flip angle of 25 degrees, to obtain the signal, and once using a 0 degree flip angle, to collect a noise measurement. In addition, a $B_1^{+}$ map was acquired using the pre-saturation turbo flash method [38]. The same series of experiments was repeated using three identical HICs. The same axial slice through the center of all three loops was used throughout all measurements. SNR maps were calculated in Matlab as outlined by Kellman & McVeigh [39]. Receive profiles were derived using a body coil reference image (same sequence parameters), and the optimal SNR coil combination was used to combine the individual images [4]. The $B_1^{+}$ maps were used to normalize the SNR and remove transmit field variations due to dielectric effects inside the phantom.

Phantom experiments similar to those described earlier were also performed on a cylindrical phantom (16.9cm diameter) filled with a liquid of identical composition (σ = 0.53 S/m) to that filling the rectangular phantom. The support of the cylindrical phantom did not allow coils to be placed beyond the centerline, thus limiting the maximum center to center distance between coils (measured along the circumference of the cylinder) to 11.2 cm (−30%). Because it was more difficult to place the coils accurately on the cylindrical surface, the whole series of experiments was performed twice and the mean of the two series is displayed in supplemental figure 4.

Finally, we also measured the SNR obtained with a single LIC, a single 3D printed HIC, and a single RG178 HIC element (same sequence parameters).

All experiments were performed on a 3 Tesla MR system (Skyra, Siemens, Erlangen, Germany), using the body coil for transmission.

Glove coil construction

Extra-long black cotton gloves were used to construct the glove coil. Although our 3D printed coils are flexible, it is not clear how the 3D printed polycarbonate material will withstand repeated bending. Instead, we elected to use RG178 coaxial cable, which has properties similar to our 3D printed design (Fig. S15). The RG178 contains a durable Teflon substrate seamlessly encasing the inner conductor. Heat shrink was used to insulate the break in the conductive braid on the far end of the coil. The same interface boards as described above were used to mount the detuning circuit and the impedance transformation circuit. Five coils were stitched along the contours of the fingers, one for each finger. The inductance of the HIC also depends on the shape of the coil (Fig. S10). When the HIC elements are bent in the glove coil, for example when a finger is curled, the frequency will change slightly. Therefore, the finger coils were tuned in a slightly bent configuration. These five coils have a slightly larger inductance due to their elongated shape, leading to a circumference of 315mm. Two additional coils were stitched on the top of the glove, one centered on the hand, and the second centered on the wrist. The final coil was stitched on the bottom of the glove, partially covering the wrist and hand. These three circular coils have a circumference of 252 mm. All elements were tuned to the same resonance frequency.

The preamplifiers (Siemens, Erlangen, Germany) were mounted on a bracelet fashioned out of acrylic plastic and connected to the MR system using a vendor specific ODU connector (ODU-USA, Camarillo, CA, USA). Two cable traps were placed on the cable connecting the preamplifiers to the scanner. The glove coils were connected to the preamplifiers through a shielded cable trap using the same thin coaxial cables found in the cable provided by ODU. The cable length from the preamp to the cable trap was 12cm and from the cable trap to the HIC elements 22cm.

Before in vivo experiments, the detuning circuits were tested on the bench and using phantom experiments in the scanner. During the phantom experiments the difference in transmit reference voltage, with and without the glove coil present, was found to be less than 1%, and no noticeable distortions could be observed in the transmit field distribution. An infrared camera (E60bx, FLIR Systems, Wilsonville, USA) was used to image the surface temperature of the glove and interface before and after a 15min interval of high applied power (100% specific absorption rate). No significant temperature differences were observed (ΔT ≪ 5C°).

In vivo experiments

High resolution T1 weighted images of the left hand were acquired at 3 Tesla using the body coil for transmission and the glove coil for reception. The volunteer was imaged in a prone position on the scanner bed, with the left hand stretched out in front of her. In the first experiment, the hand was placed flat on the table. Low resolution GRE images were used to localize the hand inside the scanner. High resolution (250μm) T1 weighted turbo spin echo (TSE) images of the left hand were acquired in coronal and sagittal planes (TSE, 1024×786 matrix, 256×192mm field of view, 2mm slice thickness, Turbo factor 2, excitation/refocusing angle of 90/180 degrees, TR = 400 ms, TE = 15ms, total scan time 2min:37sec). In addition, 150μm resolution images were acquired in sagittal only (TSE, 2048×512 matrix, 303×76mm field of view, 2mm slice thickness, Turbo factor 2, excitation/refocusing angle of 90/180 degrees, TR = 400 ms, TE = 15ms, total scan time 1min:42sec) In the second experiment, with the same general setup, the volunteer was holding a peach. After localization, a second series of coronal and sagittal T1 weighted TSE images was acquired (same sequence parameters as before). In addition, a proton density weighted 3D GRE dataset was acquired covering only a single finger (0.5 mm isotropic, 512×64×104 matrix, 256×32×52 mm field of view, TR = 12ms, TE = 5ms, 10 degree flip angle, total scan time 1min 20sec).

A second volunteer was scanned at 3 Tesla to capture the dynamics of a hand moving inside the scanner. The volunteer was imaged in a prone position on the scanner bed, with the left arm in front. During the first experiment, the volunteer was asked to move her fingers as if playing piano or typing. While the subject moved, 4000 radial projections were acquired in a coronal plane through the hand (Golden angle radial GRE, 0.8×0.8mm, 192×192 matrix, 160×160mm field of view, 2.5mm slice thickness, TR = 6.5ms, TE =3.5ms, total acquisition time 25 seconds). From these 4000 projections, 260 images were reconstructed at 10 frames per second, using a sliding window reconstruction spanning 100 projections [40].

In a second experiment, a peach was placed within reach of the volunteer, on top of the patient table. An axial slice was positioned through the center of the peach. Because there are no coil elements on the peach, the laser positioning system on the scanner was used to locate the appropriate slice. During dynamic MR data acquisition (using the same golden angle radial sequence as before), the subject reached out to grasp the peach.

Finally, a third volunteer was scanned using both the HIC glove coil and three state-of-the-art LIC-based phased arrays (Fig 5). Each of the LIC-based coils (hand, knee and head array) are built around a different plastic former. The 16-channel hand/wrist coil (Siemens Healthineers, Erlangen, Germany) was constructed on a tight-fitting clamshell, which leaves no space for the wrist, hand or fingers to move. The 15-channel knee coil (QED, Mayfield Village, OH, USA) was constructed around a 154mm cylindrical shell. The 20-channel head coil (Siemens Healthineers, Erlangen, Germany) was constructed around an 232mm domed cylindrical shell. SNR measurements were performed using the same tools described in the phantom measurements section, only this time the FOV was adjusted to 256mm and 4 averages of the body coil images were used to estimate the receive profiles. The knee coil uses a local transmit coil. In this case, the sum-of-squares image was used as a reference to construct the receive profiles. The results of the SNR comparison were further quantified by delineating the hand + wrist, palm of the hand, and fingertip in the SNR maps and calculating the average SNR value in each of these regions. The results were normalized to the average SNR observed with the state-of-the-art LIC hand/wrist coil (Table 1). In addition, a sagittal 250μm-resolution T1 weighted TSE image was acquired (using the same sequence parameters as described above

The study was approved by our institutional review board (IRB), and written informed consent was obtained prior to the examination.