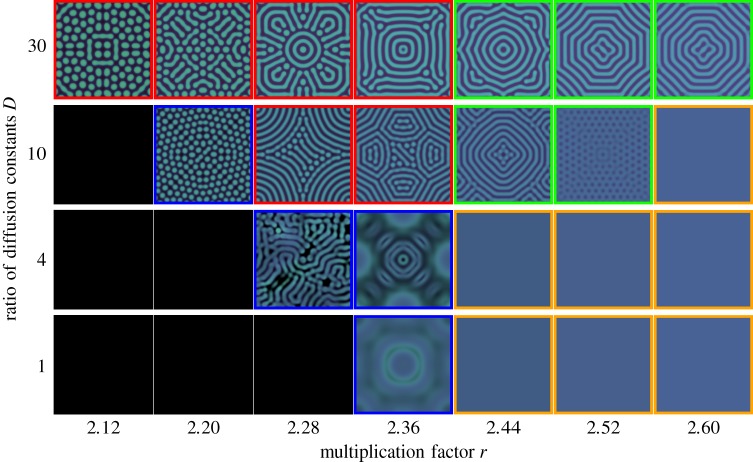
Figure 1.

Spatial patterns with various parameters (reproduced with permission from [22]). For simulating given reaction–diffusion system, we consider a two-dimensional square lattice. The space is discretized into small sites which we refer to as patches. Each subpopulation resides in each patch where they play the eco-evolutionary public goods game with a maximum group size of N = 8. For visualizing, cooperator and defector densities are presented as mint green and fuchsia pink colours and the brightness indicates the total density (see appendix D). There are five phases (framed using different colours), extinction (black), chaos (blue), diffusion-induced coexistence (red), diffusion-induced instability (green) and homogeneous coexistence (orange). Among them, chaos patterns are dynamic while others are stationary patterns. We used the Crank–Nicolson method to get patterns with a linear system size of L = 283, dt = 0.1 and dx = 1.4. All configurations are obtained after at least t = 10 000. A uniform disc with densities u = v = 0.1 at a centre is used for an initial condition. We use constant birth rate of b = 1 and death rate of d = 1.2. Note that the symmetry breaking for r = 2.28 and D = 4 arises from numerical underflow [33].