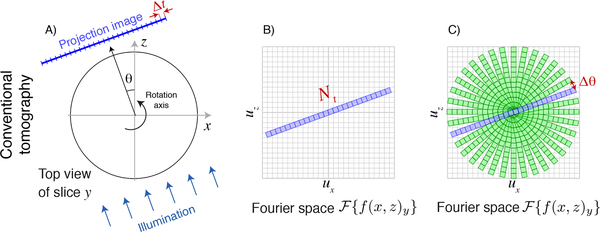
Fig. 1.

Schematic representation of the Crowther criterion in conventional tomography. In conventional tomography, each slice y of the object along the direction $\widehat{y}$ of the rotation axis is mapped onto one row of a detector. One then obtains one-dimensional pure projection images of the object with N_t transverse pixels of width Δt in the transverse direction (A), and a depth of precisely one pixel at zero spatial frequency in the axial direction (because there is no way to distinguish between different axial positions in a pure projection). For an angle θ = 0°, the Fourier transform of this image yields an array with N_x = N_t pixels in the transverse or u_x direction and N_z = 1 pixels in the axial or u_z direction in trasverse-axial Fourier space (B). As the object is rotated, so is the information obtained in Fourier space, so the (u_x, u_z) Fourier space is filled in as shown in (C). The Crowther criterion of Eq. 3 is effectively a statement that one must provide complete, gap-free coverage of all pixels around the periphery in transverse-axial Fourier space.