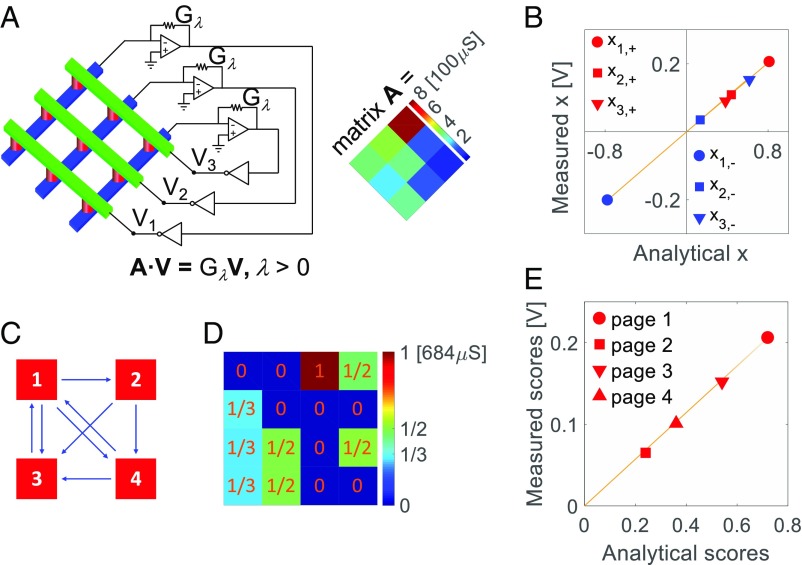
Fig. 3.

Eigenvector and PageRank calculations. (A) Cross-point circuit for the solution of the eigenvector equation Ax = λx, where x is the eigenvector and λ is the highest positive eigenvalue of a positive matrix A reported in the inset. To prevent set/reset disturb to the RRAM conductance, the output voltages of the OAs were limited to ±0.2 V. (B) Measured eigenvectors corresponding to the highest positive eigenvalue and the lowest negative eigenvalue, as a function of the normalized eigenvectors obtained by analytical solutions. The highest positive eigenvalue and the lowest negative eigenvalue were stored as the feedback conductance G_λ of the TIAs with conductance of 940 and 331 μS, respectively. (C) A system of four webpages with their respective links. An arrow pointing from page i to page j indicates a citation of j in page i, thus the importance of a webpage can be stated from the number of arrows pointing at that page. (D) The link matrix for the system in C. The elements in each column sum to 1, while diagonal elements are all null as pages do not cite themselves. The transformation unit was G₀ = 684 μS for RRAM conductance, to minimize RRAM nonlinearity. The highest positive eigenvalue is 1, corresponding to feedback resistors with conductance G₀. (E) Measured eigenvector, representing the importance scores of four pages, as a function of the analytically solved normalized eigenvector.