Abstract
The relevance of human primary motor cortex (M1) for motor actions has long been established. However, it is still unknown how motor actions are represented, and whether M1 contains an ordered somatotopy at the mesoscopic level. In the current study we show that a detailed within-limb somatotopy can be obtained in M1 during finger movements using Gaussian population Receptive Field (pRF) models. Similar organizations were also obtained for primary somatosensory cortex (S1), showing that individual finger representations are interconnected throughout sensorimotor cortex. The current study additionally estimates receptive field sizes of neuronal populations, showing differences between finger digit representations, between M1 and S1, and additionally between finger digit flexion and extension. Using the Gaussian pRF approach, the detailed somatotopic organization of M1 can be obtained including underlying characteristics, allowing for the in-depth investigation of cortical motor representation and sensorimotor integration.
Keywords: Somatotopy, Motor cortex, Somatosensory cortex, Population Receptive Fields, Sensorimotor integration, High-field fMRI
1. Introduction
Cortical sensorimotor areas in the human brain have been shown to exhibit somatotopic organizations at least at the macroscopic level between limbs. Perhaps best known is Penfield’s homunculus (Penfield and Boldrey, 1937) which shows a coarse distribution of body part representations on both the precentral (i.e. primary motor cortex, or M1) and postcentral gyri (i.e. primary somatosensory cortex, or S1) in humans. It has also been demonstrated that S1 exhibits a somatotopic organization on a mesoscopic ‘within limb’ level for individual finger digits (Kolasinski et al., 2016; Martuzzi et al., 2014; Sanchez-Panchuelo et al., 2012). However, for M1 the existence of such a detailed orderly functional organization is still under debate. It has even been argued that M1 explicitly does not have an orderly somatotopic organization on the mesoscopic ‘within limb’ level (Sanes and Schieber, 2001; Schieber, 2001). It is argued that the human ability for acquiring new motor skills could require the brain to maintain a flexible attitude towards cortical motor organization. This poses several challenging questions, specifically how movement of body parts is represented within the human brain, and also how sensorimotor integration is accomplished if M1 is not somatotopically organized and could additionally change its organization over time depending on newly acquired motor skills.
Numerous studies have investigated the nature of M1 functionality in humans and animals over the past decades. Central to the investigation of the primary motor cortex is the issue of what its neuronal activity represents and how it relates to motor functioning. The first possibility is that M1 neurons directly send commands to specific motor units/muscle fibers (Kakei et al., 1999; Scott, 2012). However, with the use of viral tracers it has been shown that a single muscle receives input from a relatively large cortical region within M1 (Cheney and Fetz, 1985; Rathelot and Strick, 2009). Additionally, electrophysiological stimulation at single sites within M1 results in the display of complex movements, often accompanied by specific body and limb postures (Brown and Teskey, 2014; Graziano and Aflalo, 2007). It appears that individual neurons or even small neuronal populations do not send commands to individual muscles or motor units. Instead, M1 activity relates to complex motion behavior, where neuronal populations code for the building blocks of complex movements, or “muscle synergies”, that together constitute a person’s full motion repertoire (d’Avella et al., 2006; Ting and McKay, 2007). Such complex motion representation can arguably not be encapsulated in an orderly cortical topography, although a coarse categorization on the basis of related body parts or limbs could be computationally beneficial.
Recently, imaging studies have also engaged in the characterization of M1 activity in humans. Several studies show that the movement of individual finger digits results in largely overlapping activity patterns, showing voxels that respond to all finger movements (Dechent and Frahm, 2003; Hlustík et al., 2001; Olman et al., 2012). A somatotopic organization of M1 at the level of individual finger digits is not immediately distinguishable and can primarily be appreciated after extended analyses, contrasting activity patterns of individual finger digits. Previous findings, thus, show that M1 might contain a somatotopic organization at the mesoscopic level of finger digits, while it simultaneously responds to a much larger range of bodily movements. The complexity of a neatly ordered somatotopy on the one hand, and a more diffuse activity pattern for many motor actions on the other hand, might well be characterized by a Gaussian function. Gaussian functions are able to describe the correspondence of (cortical) functioning with respect to measured neuronal activity patterns (Victor et al., 1994). Gaussian functions have been shown to successfully describe neuronal characteristics including topographies in research concerning sensory cortices, which has led in imaging studies to the population Receptive Field (pRF) approach to accurately assess the retinotopic organization in visual cortex (Dumoulin and Wandell, 2008; Harvey and Dumoulin, 2011).
The current study investigates whether a detailed, yet complex, somatotopic organization of cortical area M1 can be obtained through the implementation of a Gaussian pRF approach during finger movements. The Gaussian pRF approach is novel to the modeling of cortical motor activity for both motor and somatosensory cortex, and is here implemented analogously to the pRF approach in visual cortex. Note that this means that the Gaussian function is not to be fitted across spatial cortical activity patterns, but instead on functional features of neuronal populations. Functional features of motor cortex are in fact control over and/or information processing of certain limbs, i.e. finger digits in the current experiments, which can be probed by means of a simple finger movement task. Based on previous research, neuronal populations in M1 are expected to respond to a wide variety of functional features, which is described by a Gaussian fit with a center feature corresponding to a population’s preferred finger digit and a Gaussian spread corresponding to the degree of response to adjacent finger digits. In sensory cortices the Gaussian spread is often referred to as a neuron’s receptive field (RF), or the average neuronal population receptive field (pRF). Through the Gaussian pRF approach, we show that an orderly somatotopic organization of preferred finger digits is present in M1. Additionally, we reveal differences as well as similarities in properties of population receptive fields between flexion and extension of finger digits and across separate cortical areas in the contralateral hemisphere.
2. Materials & Methods
2.1. Subjects and task
Eight healthy volunteers (mean age = 24, female = 4) were recruited from the Utrecht University. All participants gave written informed consent before entering the study. The protocol was approved by the local ethics committee of the University Medical Center Utrecht, in accordance with the Declaration of Helsinki (2013).
All participants performed a simple finger movement task with their right hand. The primary task objective was to isolate movements of individual finger digits as well as movement type, i.e. dissociate flexion from extension. Task instructions were projected on a screen in the bore of the scanner, which participants viewed using prism glasses and a mirror. The instruction onsets were triggered by the scanner. During the experiment, the participants viewed 5 rectangles on a grey background that together resembled the shape of the 5 finger digits of a hand. Each rectangle represented the instruction for its respective finger digit, which was denoted by the rectangle’s contrast. During the entire experiment, when a rectangle was displayed having a white contrast, that respective finger digit was to be flexed. Finger digit extension was cued when the contrast changed to black. The rectangles were only displayed having a black or white contrast, meaning that each finger digit was always flexed or extended and there was no separate rest condition. The order of rectangle contrast change occurred in a sequential manner. Initially, all 5 rectangles started out having a black contrast, which meant that the participant assumed a fully extended hand position. Then one by one, the rectangles became white starting from either the thumb or the little finger, moving its way across all finger digits and ending with a fully flexed hand (i.e. all white rectangles). Afterwards, all 5 rectangles became black again in sequential order from thumb to little finger or vice versa, resulting in the sequential extension of each finger digit. By doing so, we obtained separate flexion and extension runs, which were both repeated 8 times (4x starting from the thumb and 4x starting from the little finger). The time between two sequential movement cues was 4.8s, except for the last of the 5 digits and the first of the next run, which had an interval of 14.4s allowing the Blood Oxygen Level Dependent (BOLD) signal to return to baseline prior to the new sequence of movements. Making the cue interval shorter than approximately 5 seconds (4.8s was chosen as a multiple of the TR of 1.6s, see scan protocol) would result in the inability to effectively distinguish BOLD signals following a movement cue, while making it longer would increase the risk of decreasing attention and task performance.
Thus, the BOLD signal is expected to increase following a movement cue only, rather than during the maintaining of finger positions (Branco et al., 2017). Keeping digits flexed or extended, therefore, serves as the baseline for digit movement. Finger digits that maintain their position might cause neuronal activity, but not specifically at the time-locked events of the motor cues. Finally it is worth mentioning that the participants were explicitly instructed to disregard any co-occurring movements. Some finger digits are enslaved in the movements of others (e.g. due to tendon connections). Participants were expected to only perform the cued motor command and not to correct for any co-occurring movements. Compliance with the task instructions was tested using a MR-compatible data glove (5DT Inc.)
2.2. Scan protocol
Scanning was performed on a 7 Tesla Philips Achieva scanner (Philips Healthcare, Best, Netherlands) with a 32-channel receive headcoil (Nova Medical, MA, USA). Functional MRI (fMRI) measurements were obtained using an echo-planar imaging (EPI) sequence with the following parameters: SENSE factor=3.0, TR=1600 ms, TE = 27 ms, flip angle = 70°, axial orientation, interleaved slice acquisition, FOV (AP, FH, LR) = 208.8 x 41.6 x 208.8 mm3. The acquired matrix had the following dimensions: 132 x 26 x 132, voxel size: 1.6 x 1.6 x 1.6 mm3. The functional images were acquired from the superior 42 mm of the brain, covering the majority of the frontal and parietal lobes. During the functional image acquisition, 8 flexion runs and 8 extension runs were performed by each participant, where a single movement run took 21 images to complete (4 x 4.8s + 14.4s). Also a rest block of 9 images (14.4s) was acquired at the start of the experiment, resulting in a total of 345 functional images per participant. A T1-weighted image of the whole brain (0.49 x 0.49 x 0.8 mm3, FOV = 512 x 512 x 238) and a whole-brain proton density image (0.98 x 0.98 x 1.0 mm3, FOV = 256 x 256 x 190) were acquired at the end of the functional sessions.
2.3. Image processing
The T1-weighted image was corrected for macroscopic field inhomogeneities by dividing it by the proton density-weighted image (Van de Moortele et al., 2009). Grey/white matter surfaces were constructed on the basis of the corrected T1-weighted image using Freesurfer (http://surfer.nmr.mgh.harvard.edu/, (Dale et al., 1999)). The reconstructed brain surfaces are triangulated surface meshes, where each triangle consists of 3 nodes (sometimes called vertices), while the entire surface mesh contains over 100,000 nodes per hemisphere. All reconstructed surface meshes were flattened using Caret (Van Essen et al., 2001) and rotated so that the central sulcus was oriented vertically. All functional images were preprocessed (i.e. slice time correction and realignment to the mean scan, no smoothing) using SPM12 (http://www.fil.ion.ucl.ac.uk/spm/). The preprocessed functional images were mapped onto the Freesurfer surfaces, selecting all voxels that fell in range of the estimated grey matter thickness. This procedure resulted in a timeseries for each surface node of the reconstructed surfaces. The timeseries were filtered using a high-pass filter with a cut-off at 9.1 x 10-3 Hz and rescaled to represent percentage signal change. Finally, all timeseries were split in 2, creating separate timeseries for all flexion and extension runs. For the Gaussian pRF analysis we only considered the surface nodes that were located on the ‘precentral gyrus’, ‘central sulcus’, and ‘postcentral gyrus’, as defined by the Destrieux altas (Destrieux et al., 2010) supplied by Freesurfer.
2.4. Gaussian pRF analysis
It is common practice in fMRI analyses to predict acquired timeseries of voxels (or nodes/vertices in surface based analyses) using a general linear model (GLM) which includes a design matrix convolved with a HRF (Friston et al., 1995). The strength of each factor in the design matrix is usually presented as β (beta). Finding Gaussian population Receptive Fields (pRF) does not differ much from the classical approach, but incorporates a parametrized model of underlying neuronal populations, its value being that the obtained parameters meaningfully relate to the behavior of neuronal populations. Obtaining pRF fits was based on the procedures described by Dumoulin & Wandell (Dumoulin and Wandell, 2008). The main objective was to model a predicted timeseries that best explained the variance of the measured fMRI timeseries:
| (1) |
where y(t) is the measured timeseries, p(t) is the model predicted timeseries, β is the scaling factor and ε is measurement noise. The main component of the model predicted timeseries was a Gaussian function. The input to the Gaussian function is an index of the finger digit that was moved (i.e. an index ranging from 1 to 5 corresponding to the 5 finger digits). Given a Gaussian center and Gaussian spread (i.e. standard deviation) the relative amplitude with respect to a specific digit movement is then given by:
| (2) |
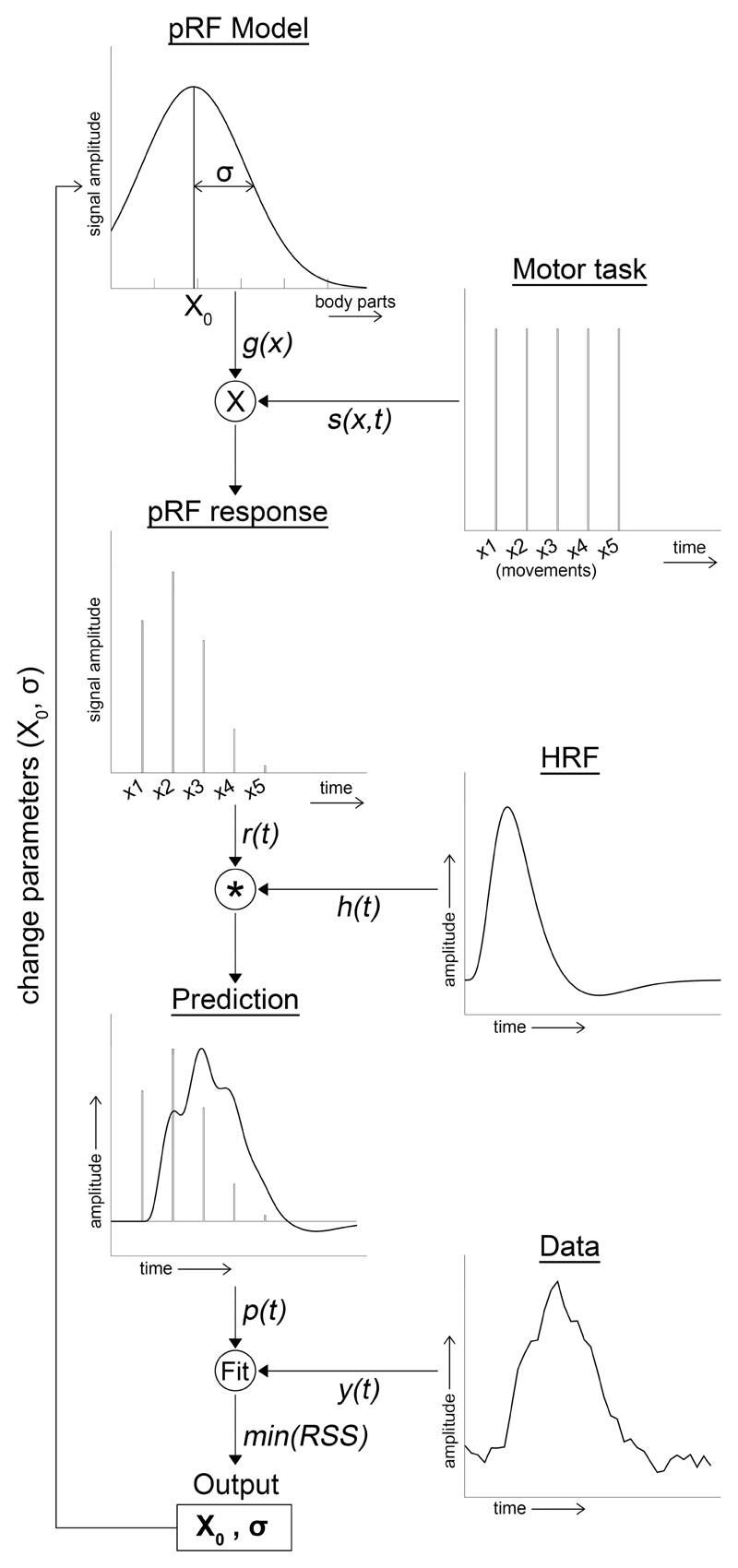
where xi is the index of the moved finger digit (ranging from 1 = thumb to 5 = little finger), and x0 is the Gaussian pRF center (also ranging from 1 to 5). σ is the Gaussian spread, which defines the activity for finger digit movement relative to x0. The unit for σ is the same as the unit for x0, which is, thus, also given in finger digit indices. Note, however, that the pRF center x0 can be any real number between index 1 and 5, including fractioned numbers in between 2 finger digit indices. Thus, function (2) describes for a given neuronal population what its preferred finger digit is (i.e. the pRF center, x0), but also how that neuronal population responds to the movement of other finger digits. The bigger the Gaussian spread (i.e. its receptive field size, σ), the more it responds to digits other than its preferred finger digit (Figure 1, pRF model).
Figure 1. Flowchart pRF analysis.
Schematic of the pRF analysis. For full details, see text section 2.4.
Afterwards, the effective task design was constructed (Figure 1, pRF response). The input for the effective task design was the onset design matrix of each finger digit movement (Figure 1, Motor task) multiplied by the Gaussian function (2). This procedure resulted in a Gaussian model timeseries for each finger digit movement (i.e. 5 digits x 2 flexion/extension) and was summed to create a single Gaussian model timeseries per movement type (i.e. timeseries for flexion and extension each):
| (3) |
Where s(x,t) is the onset design matrix of each finger digit movement and g(x) is the Gaussian function (2). The Gaussian model predicted timeseries is then obtained after convolution with a standard canonical hemodynamic response function (HRF, (Friston et al., 1995)).
| (4) |
where, r(t) is the effective task design (3), and h(t) is the canonical HRF (Figure 1, Prediction).
We adopted a 2-step coarse-to-fine search approach to find the best Gaussian model fits. For the first step, the coarse search, we predefined 176 Gaussian models using function (4) with varying Gaussian centers and standard deviations (i.e. 11 Gaussian center indices ranging from 0.5 to 5.5 with steps of 0.5 x 16 Gaussian standard deviation ranging from 0.25 to 4.0 with steps of 0.25). We calculated Pearson correlation values for all Gaussian models and the flexion/extension timeseries of each surface node. The nodes of which any of the Gaussian models explained at least 15% of the variance within the timeseries were included in the second step: the fine search. The fine-search fitted the complete function (1) using the Levenberg-Marquardt algorithm (LMA), which is a least square minimization algorithm (Markwardt, 2009). As initial parameters, the model parameters corresponding to the model with the highest correlation from the coarse-search were chosen. Constraints were applied within the LMA to limit Gaussian centers to the finger digit range, and the Gaussian spread to a maximum of 4. The latter was done, due to the fact that only 5 different movements were performed, on which the Gaussian standard deviation is based. A Gaussian spread much larger than 4 cannot be reliably estimated with only 5 separate movements. The allowed fitting range of Gaussian centers was extended by a half in the direction of the thumb and little finger in order to obtain equal ranges for each finger digit (i.e. thumb=[0.5 : 1.5]; index finger=[1.5 : 2.5] ; middle finger=[2.5 : 3.5] ; ring finger=[3.5 : 4.5] ; little finger=[4.5 : 5.5]). After the fitting procedure, a goodness-of-fit F-statistic and p-value were calculated. For the statistical analysis, only the surface nodes in precentral gyrus, central sulcus and postcentral gyrus (Destrieux atlas) were included with p < .05, Bonferroni corrected.
2.5. Statistical analysis
The main objective was to test for the presence of a somatotopy in the precentral gyrus, central sulcus and postcentral gyrus. We define a somatotopic organization of finger digits as a sequential gradient of Gaussian centers across the cortical surface. Therefore, we tested for a linear relationship between the estimated Gaussian centers and the coordinates of the included flattened surface nodes. The flattened surface was rotated so that the central sulcus was oriented vertically, which meant that the maximum gradient in somatotopic organization was expected along the Y-axes of the 3 included regions of interest (ROI): the precentral gyrus, central sulcus and postcentral gyrus. We calculated linear regression coefficients for the fits between Gaussian centers and Y-coordinates, which were used in a second-level group analysis. A positive regression coefficient meant that there was a linear relation between Gaussian centers and Y-coordinates with the thumb located ventrally and little finger located dorsally. A negative regression coefficient meant a reversed linear somatotopic order (i.e. thumb located dorsally and little finger ventrally). Finally, regression coefficients around zero are to be interpreted as no evidence for a linear relation between Gaussian center and cortical coordinates. Whether regression coefficients differed significantly from zero across participants was tested with a student’s t-test per ROI.
Since information on receptive field properties of neuronal populations in sensorimotor cortex is scarce, we did not hypothesize a linear relation between Gaussian spread (i.e. receptive field size) and Gaussian centers. Instead, we averaged the Gaussian spread in 5 bins corresponding to the indices of the 5 finger digits, resulting in a mean Gaussian spread per finger digit representation per ROI. Using a repeated measures ANOVA with the 5 bins and the 3 ROIs as separate factors, we investigated if there was an effect of the estimated Gaussian center and/or ROI on Gaussian spread. This was done separately for finger flexion and extension. Similarly, the estimated amplitude was also averaged in finger digit bins per ROI. We used a repeated measures ANOVA with the 5 finger digit bins, 3 ROIs, and a separate factor for flexion/extension to investigate differences in BOLD amplitude among the flexion/extension conditions.
Lastly, we redid the analysis using a standard multiple general linear model (GLM) for comparison. The GLM consisted of 5 factors (one for each finger digit, movement types flexion/extension separately), which resulted in 5 β-weights per surface node per movement type. A winner-takes-all procedure was applied, which meant that the preferred finger digit was assigned by means of the highest ranked factor of the GLM per surface node.
2.6. Data glove
The data glove sampled the flexure of each finger digit at a frequency of 20Hz (i.e. a timeseries per finger digit reflecting finger flexure). The timeseries of each digit was normalized to z-scores:
| (5) |
where, dg(x,t) is the raw data for finger digit x at time t, and are the mean and standard deviation of the timeseries for finger digit x respectively. Then, the first derivative of the normalized timeseries was estimated:
| (6) |
Where ∂(x,t) is an approximation of the first derivative, resulting in sharp increases during the moments of flexion or extension (note that the absolute value was taken). Finally, the maximum value was taken of each finger digit within a time window of [ti-500ms : ti+1500ms] for each presented movement cue ti, and averaged over repetitions. The time window, thus, allowed us to control for any movement onset deviations relative to the presented cue. Also note that the maximum values of all 5 digits were taken during any movement cue to check for co-occurring movements relative to the cued finger digit. This was statistically tested using a repeated measures ANOVA with factors for the 5 motion cues, the 5 finger digit traces, and flexion/extension conditions. Finally, Pearson correlation values were calculated between Gaussian spread and conjoint movements (i.e. the amount that finger digits had moved when they were not cued). Conjoint movements were calculated for each finger digit trace per subject and correlated to the obtained Gaussian spreads per cortical area and movement type (i.e. flexion/extension).
3. Results
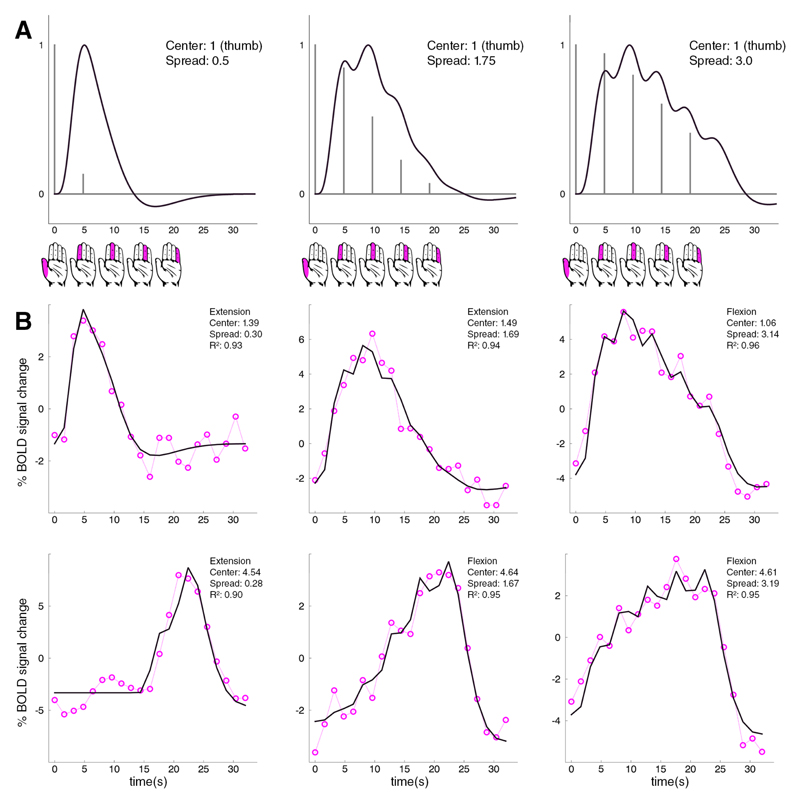
We developed a Gaussian pRF model that predicted the timeseries for finger digit flexion and finger digit extension. The timeseries’ peak amplitude was determined by a neuronal population’s preferred finger digit, while predicted amplitudes elicited by movement of the other finger digits were characterized by the Gaussian spread (Figure 2A). The Gaussian pRF model significantly predicted the timeseries of on average 2400 surface nodes (S.D. 750 nodes) per subject, which were mainly located around the cortical hand area. The percentage of BOLD signal change followed the cues of the motor task, and did not show sustained increases in neural activity in between flexion/extension runs (Figure 2B). The presence of an ordered somatotopy was determined based on the collective locations of estimated preferred finger digit representations across motor and somatosensory cortex (Figure 3).
Figure 2. fMRI timeseries with fitted pRF models.
The top row (A) shows 3 examples of pRF models with increasing Gaussian spread, while the Gaussian center remains constant at 1 (the thumb). For each timeseries, 5 movement cues of each finger digit were presented every 4.8s, which is depicted by the hand icons below. Since the Gaussian center is held constant at 1, the peak response is predicted for the thumb movement (grey vertical lines). Responses to other movement cues decrease according to the Gaussian function. The black line depicts the Gaussian modified impulse responses after convolution with a canonical HRF.
The two bottom rows (B) show 6 timeseries of measured BOLD responses (dashed pink lines+circles) and the fitted Gaussian pRF models (black lines). The depicted BOLD timeseries were taken from subjects 3 to 8. The first 3 graphs of (B) show pRF fits with increasing receptive field size, while the pRF center is remains on around the thumb movement (center within range of [0.5 : 1.5]). The bottom row similarly shows pRF fits with increasing receptive field size, only the fits are centered on the little finger (center within range of [4.5 : 5.5]). Movement sequence is from thumb to little finger for all presented graphs (depicted by the hand icons).
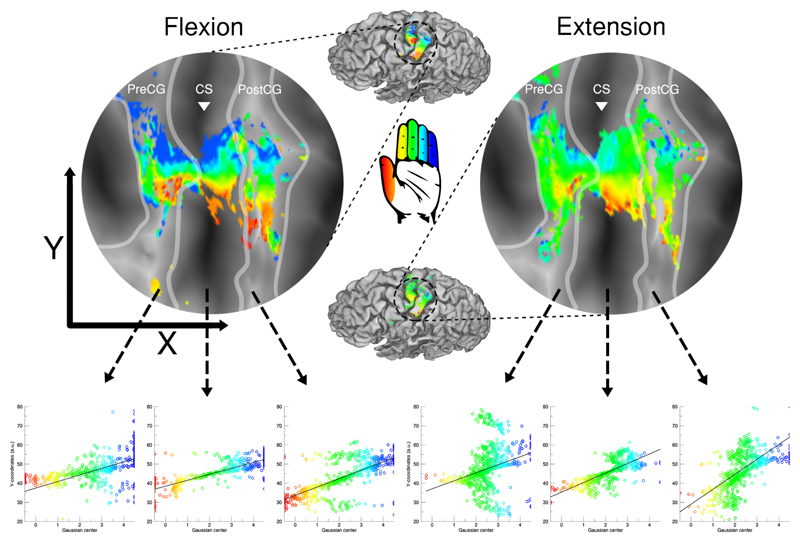
Figure 3. Somatotopic maps with linear regression.
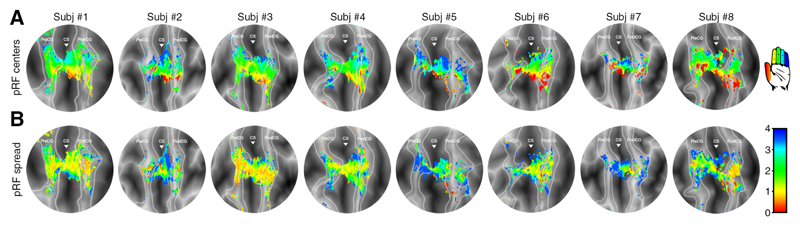
The figure depicts the somatotopic maps of 1 subject for finger flexion (top left) and extension (top right). For the 3 included cortical areas (i.e. precentral gyrus, central sulcus and postcentral gyrus) a regression analysis was performed to determine the presence of an ordered somatotopic map along the Y-coordinates of the flattened surface (bottom row). The borders of the cortical areas are given by the light grey lines and the white triangle is aligned with the base of the central sulcus. The estimated finger digit representation is color coded: thumb representation is presented in red up to the little finger representation in blue.
3.1. Finger flexion
We examined the pRF results during the sequential flexion of the 5 finger digits of the right hand in the contralateral hemisphere. We found proof of orderly somatotopic organizations in sensorimotor cortex. The preferred finger digit representation gradually shifted from thumb to little finger on the cortical surface from ventrolateral to dorsomedial locations respectively. During flexion of the finger digits, a somatotopy was found on the cortical surface of the contralateral precentral gyrus (t(7)=4.678, p=.002), central sulcus (t(7)=5.400, p=.001), and postcentral gyrus (t(7)=10.804, p<.001) across subjects (Figure 4A). Cortical area M1 is approximately located on the crown and posterior bank of the precentral gyrus. We, thus, present proof for an ordered finger digit somatotopy within M1 given the significant gradient of preferred finger digit representations in both the precentral gyrus and central sulcus regions. The postcentral gyrus also exhibited a clear gradient of preferred finger digit representations, meaning that the pRF method also revealed the finger digit topography of cortical area S1. Note, however, that the finger digit somatotopy could also largely be derived using a general linear model (GLM), although visibility of an ordered finger digit somatotopy decreased on the precentral gyrus (Figure 4A). In addition, we found that individual finger digit representations within cortical areas M1 and S1 were largely interconnected (Figure 5A). Representations of the same finger digit in M1 and S1 are connected, creating extended strips of preferred finger digit representations along the anterior-posterior axis of the cortical surface, which could not always be appreciated from a pial surface perspective (see also Figure 3).
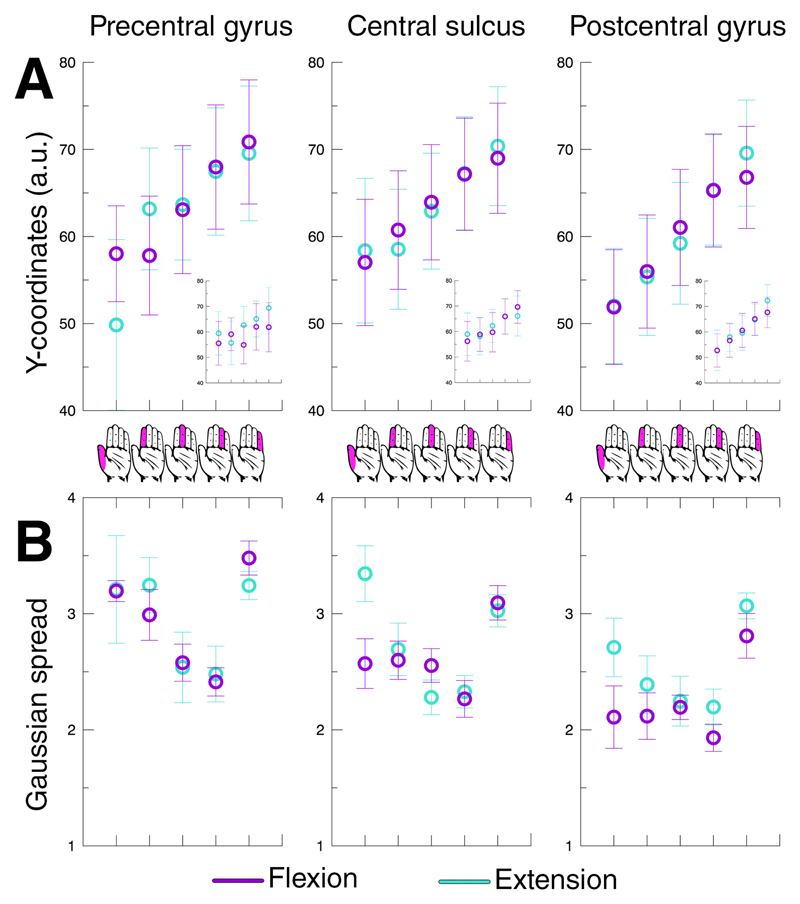
Figure 4. Average finger digit location and pRF size.
The top row depicts the average Y-coordinate on a flattened reconstructed cortical surface for finger digit flexion (purple) and extension (cyan) across the 3 included cortical areas (A). Additionally, the results of a standard GLM analysis are presented per cortical region by the smaller graph-within-graphs. The bottom row shows the Gaussian spread averaged over subjects per finger digit representation (B). The error bars depict the standard error of the mean across subjects. The hand icons in the middle of the figure represent the legend of the horizontal axis for all graphs, referring to the corresponding finger digits per depicted data point.
Figure 5. Finger digit flexion pRF maps.
pRF results projected on flattened surfaces of all 8 subjects during finger digit flexion. The borders of the included cortical areas are given by the light grey lines and the triangle is aligned with the base of the central sulcus. The top row (A) shows the estimated Gaussian centers, which together constitute the finger digit somatotopy. The estimated finger digit representation is color coded (see icon on the top right): thumb representation is presented in red up to the little finger representation in blue. The bottom row (B) depicts the Gaussian spread or receptive field size. The Gaussian spread is color coded (see bar at the lower right). Red colors depict small receptive fields, whereas blue colors depict larger receptive fields.
The second outcome of the pRF analysis is the Gaussian spread (or pRF size), corresponding to the degree of response to other finger digits besides the preferred finger digit (Figure 4B, 5B). The unit for the Gaussian spread is given in finger digits, meaning the larger the spread the more finger digits a neuronal population responds to. We found that the Gaussian spread depended on the estimated preferred finger digit (F(4,28)=21.126, p<.001), resulting in relatively small pRFs for thumb representations and larger pRFs for little finger representations, although the relation between Gaussian spread an finger representation is not evidently linear. There was also a difference in Gaussian spread across cortical areas (F(2,14)=15.456, p<.001), showing largest pRF sizes on the precentral gyrus and smallest pRF sizes on the postcentral gyrus (Figure 4B). Thus, the pRF sizes follow general distinctions found for the estimated finger digit representations, as well as anatomical differentiation.
3.2. Finger extension
During extension of the right hand finger digits, we did not find an ordered somatotopic arrangement of Gaussian centers in the contralateral precentral gyrus (t(7)=1.908, p=.098). However, we did observe detailed somatotopic organizations in the central sulcus (t(7)=7.896, p<.001) and postcentral gyrus (t(7)=6.436, p<.001) during finger digit extension (Figure 6). Since we did not observe significant gradients of estimated preferred finger digits in both the precentral gyrus and central sulcus, we cannot conclude that area M1 displays an ordered finger digit topography during finger digit extension. We did observe that pRF sizes varied for the estimated finger digit representations (F(4,28)=10.415, p<.001), as was also seen for finger digit flexion. However, for finger digit extension the pRF sizes of both the thumb and little finger were relatively larger compared to the remaining 3 digits. Additionally, the receptive field sizes for finger extension did not vary across the 3 cortical areas (F(2,14)=2.892, p=.089), thereby not exhibiting the gradual decline in receptive field size from precentral gyrus to postcentral gyrus that can be observed for finger digit flexion (Figure 4B). No difference in estimated BOLD amplitude was observed between finger digit flexion and extension (F(1,7)=0.004, p=.952). These findings indicate that finger digit extension resulted in clear positive BOLD signals within M1, similar to finger digit flexion. The pRF outcomes, however, did reveal certain differences in somatotopy and receptive field size, which could point towards different underlying mechanisms.
Figure 6. Finger digit extension pRF maps.
pRF results projected on flattened surfaces of all 8 subjects during finger digit extension. The borders of the included cortical areas are given by the light grey lines and the triangle is aligned with the base of the central sulcus. The top row (A) shows the estimated Gaussian centers, which together constitute the finger digit somatotopy. The estimated finger digit representation is color coded (see icon on the top right): thumb representation is presented in red up to the little finger representation in blue. The bottom row (B) depicts the Gaussian spread or receptive field size. The Gaussian spread is color coded (see bar at the lower right). Red colors depict small receptive fields, whereas blue colors depict larger receptive fields.
3.3. Data glove
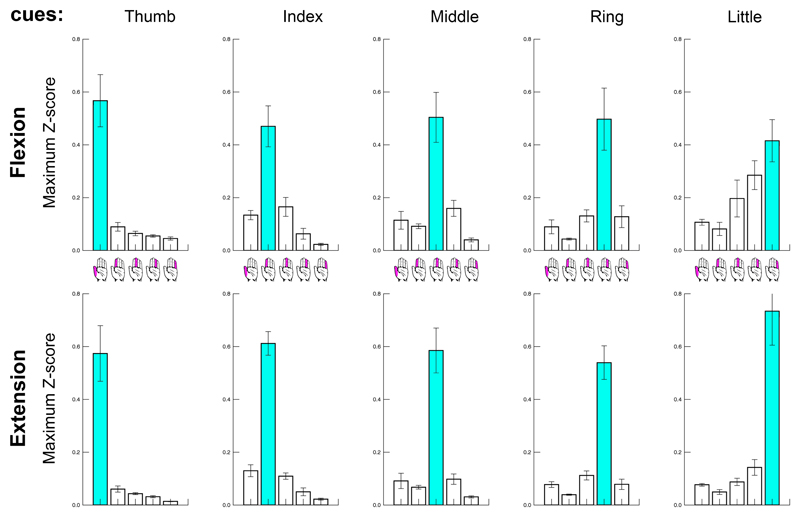
Data glove recordings of 2 participants (# 2 & 3) were discarded due to technical issues. For the remaining participants, we found that after normalization of the timeseries to Z-scores there was no difference between the maximum values of the 5 finger digit traces (F(4,20) = 1.590, p=.216), or following any of the movement cues (F(4,20) = 1.918, p=.147). Furthermore, we found no difference between the values for flexion and extension (F(1,5) = .361, p=.574). There was, however, a strong significant interaction effect between onset cue and finger digit trace (F(16,80) = 34.966, p<.001), reflecting the task requirement of moving the corresponding finger digit following a particular motion cue. Figure 7 shows that primarily the cued finger was moved in the selected time window surrounding a particular motion cue. Largest movements of non-cued finger digits were observed during the little finger flexion cue. However, we did not find that pRF spread was positively correlated with the amount of movements finger digits made when they were not cued (Table 1). For instance, the little finger stayed relatively still when it was not cued for movement, while we found it to exhibit a relatively large pRF spread, and vice versa for the ring finger digit.
Figure 7. Data glove.
Z-score normalized movement amplitude is presented per cue (5 columns from left to right), for flexion and extension (2 rows), and per finger digit recording (5 bars in each subplot, also see hand icons). The cued finger digit is colored in cyan, and is here shown to have the largest movement amplitude compared to non-cued digits for all conditions.
Table 1. Pearson correlation pRF spread and conjoint movements.
Pearson correlation values of pRF spread and conjoint movements per cortical area and finger movement type. Conjoint movements were calculated as the average of unwanted movements per data glove finger digit trace per subject.
| Precentral Gyrus | Central Sulcus | Postcentral Gyrus | |
|---|---|---|---|
| Flexion | -0.249 | -0.248 | -0.214 |
| Extension | -0.329 | -0.199 | -0.392 |
4. Discussion
4.1. General discussion
Using the population Receptive Field approach, we demonstrate that a detailed and ordered somatotopy at the level of individual finger digits exists for the primary motor cortex (M1). For M1, the thumb representation is located ventrolaterally near the hand area at the crown and posterior bank of the precentral gyrus, while M1 representations of the remaining 4 finger digits gradually shift in dorsomedial direction along the precentral gyrus. This particular structure in M1 is mainly observed for finger digit flexion and not for finger digit extension. Additionally, the Gaussian pRF approach estimates receptive field sizes (although “population response field” might be more adequate in the context of M1 neural activity). Cortical representations of the little finger digit consistently showed largest pRF sizes, indicating that those particular neural populations are relatively unspecific regarding the movement of any of the finger digits. Finally, the current experiments confirm previous reports on a detailed somatotopic structure at the level of individual finger digits for the primary somatosensory cortex (S1), albeit during finger digit movement instead of solely sensory stimulation (Martuzzi et al., 2014; Sanchez-Panchuelo et al., 2012). pRF sizes from S1 are smaller compared to M1, suggesting that sensory (feedback) information occurs at a level more specific than is observed for motor activity. We, thus, present evidence for a highly detailed somatotopic structure of M1 similar to S1. Furthermore, using the pRF approach we are able to investigate basic response characteristics of the underlying neuronal populations.
4.2. M1 somatotopy
There has long been debate on the relation of M1 to muscle activity. Previous studies have thus far only revealed a coarse somatotopic organization within M1 and in addition argued that M1 codes for complex movements rather than the movement of isolated body parts (Graziano et al., 2002; Sanes and Schieber, 2001; Schieber, 2001). However, the current approach is able to expose the detailed within-limb somatotopic organization of M1, possibly due to the inclusion of pRF characteristics and the separation of finger digit flexion and extension. The pRF approach allows for a parametrized modeling of neuronal populations’ responses, although a finger digit somatotopy can also be approximated by more classical approaches such as general linear models (Figure 4A). Furthermore, even though we now reveal the within-limb somatotopy of M1, the Gaussian pRF model does not assume that M1 neurons respond in isolation with respect to individual body parts. Instead, the pRF approach shows that many neuronal populations respond to multiple finger movements. Complex motion might, therefore, still be represented within pRF properties, putatively grouping specific body parts that together create complex movements. Nevertheless, the locations of the Gaussian pRF centers reveal a clear somatotopic structure within M1, which may appear superfluous if neuronal populations can code for movements beyond the range of one specific body part (Meier et al., 2008; Zeharia et al., 2015). The reason for a detailed somatotopic organization in M1 may be related to sensorimotor integration. The current results show large connected patches of single finger digit representations running along motor and somatosensory cortex (Figures 5 and 6), which could possibly already have been appreciated in an earlier study on S1 somatotopy in amputees (Kikkert et al., 2016). Currently, connected patches of finger representations throughout sensorimotor cortex were seen in all subjects, despite that somatotopic maps were relatively unique per subject, often following a subject’s anatomy closely. These connected areas with different physiological properties likely interact through horizontal connections throughout sensorimotor cortex (Sporns et al., 2000). In this context, it makes sense that M1 has a detailed somatotopic structure, simply because S1 is somatotopically organized. In the current study, activity in S1 most likely relates to proprioception, containing useful information on the position of body parts during movement. This information is thought to be necessary feedback from S1 to M1 (Todorov, 2009, 2000), which advocates a similar detailed topographic organization of M1 and S1 for integration purposes. Alternatively, the joined somatotopic structure across sensorimotor cortex might have arisen as a result of joined developmental processes. It has for instance been shown that M1 and S1 share similar developmental characteristics in terms of grey matter thickness (Gogtay et al., 2004). Furthermore, corticospinal tracts connected to M1 and S1 are somatotopically organized and share similar properties compared to adjacent cortical areas (Ji et al., 2008; Seo and Jang, 2013; Verstynen et al., 2011). It is, thus, plausible that the development of M1 and S1 is strongly interdependent, as is also suggested by in vivo rodent (Khazipov et al., 2004) and simulation studies (Petersson et al., 2003). The development of motor and somatosensory cortices likely coincide with one another, giving way to sensorimotor integration and possibly interconnected somatotopic maps.
4.3. Population receptive fields
The current Gaussian pRF fitting procedure allows for the Gaussian center to be estimated anywhere in between two physical finger digits. Having the cortical finger digit representation centered in between two finger digits may seem unintuitive at first. However, there are two logical explanations that are not mutually exclusive. Firstly, we are measuring the response of neuronal populations containing over 100,000 neurons at each point on a reconstructed cortical surface (Herculano-Houzel, 2009; Lent et al., 2012). It is rather probable that multiple finger digit representations are present among neuronal populations of certain size. The estimated Gaussian center is then merely a population average, which can be expressed by fractioned numbers. Secondly, neurons in sensorimotor cortex might not code for a single preferred finger digit. It has been shown that neurons from the primary motor cortex have efferent connections to a relatively broad range of motor units/muscle fibers (Nudo et al., 1992). Motor actions might well be a complex cohort of many excitatory and inhibitory processes, allowing neurons to center their peak response over an extended range of body parts or no body part in particular (Graziano et al., 2002; Nudo et al., 1996). Then the neural ensemble contains the appropriate muscle output for e.g. a finger digit, instead of coming from individual neurons or small neuronal populations. The current estimated Gaussian center is sensitive to an off-centered body part representation relative to physical body parts, which occurs when small neuronal populations do not code for individual body parts.
The current method provides an estimate of the Gaussian spread, or response/receptive field size for neuronal populations in sensorimotor cortex. Previous studies have reported overlapping receptive fields in sensorimotor cortex (Beisteiner et al., 2001; Besle et al., 2014; Meier et al., 2008). The current study underlines these findings, showing that many neuronal populations in both M1 and S1 respond to several finger movements at least to some degree. Largest pRF sizes were found for neuronal populations in M1, indicating that neuronal populations in M1 least of all included sensorimotor areas respond in isolation with respect to any particularly moved finger digit. This finding likely relates to previous electrophysiological studies, where complex movements and postures were reported following stimulation of M1 neurons (Brown and Teskey, 2014; Graziano et al., 2002; Graziano and Aflalo, 2007). Additionally, neuronal populations that prefer the little finger digit exhibited larger pRF sizes compared to neuronal populations that prefer any of the other finger digits. However, pRF size per preferred finger digit may also have been influenced by the order of movement, i.e. whether a series of finger digit movements started at the thumb or little finger, which possibly affected the estimated pRF size at the start of a movement by e.g. transient responses (Dechent et al., 2004). Also finger digit enslavement (Li et al., 2004; Yu et al., 2010) might have influenced the estimated pRF sizes. The ring and little finger do not enjoy the same level of freedom of movement as the thumb or index finger. Possibly the enslavement of non-cued movements is reflected by the pRF size. Additionally, isometric contractions (i.e. muscle contractions that keep finger digits in place, when they are not cued for movement) may occur for highly enslaved finger digits, which could theoretically cause an overestimation of pRF sizes. However, current pRF results display relatively small pRF sizes for cortical ring finger representations, which is not to be expected if the level of enslavement would largely affect pRF size (e.g. through isometric contractions). Furthermore, the data glove results showed that participants had been able to successfully perform the task (Figure 7) except for during flexion of the little finger, when most non-cued co-occurring movements of other digits were observed. This, however, cannot have caused the relatively larger pRF sizes for little finger representations, since that would require increased little finger movements during other movement cues, rather than many finger movements during the little finger cue as is seen here.
The currently estimated pRF sizes likely reflect a level of integration among body part representations: meaning the larger the pRF size, the more a neuronal population is involved during many movements. Such a scenario would benefit the control over body parts that are often used in synchrony. Current results show that little finger representations within M1 consistently display the largest pRF size, putatively reflecting the concurrent movements of the little finger digit in combination with other finger digits during daily motor actions. Similarly, smaller pRF sizes of e.g. thumb representations might imply increased levels of response specificity and might relate to the importance of the thumb in daily motor actions.
4.4. Finger digit flexion versus extension
On average, the results for finger digit flexion and extension were very similar, showing positive BOLD signals of similar magnitude. Additionally, we did not observe any differences in task performance between flexion and extension. There are, however, several differences that might reveal distinct underlying processes. Firstly, finger digit extension did not result in a significant somatotopic organization across subjects on the precentral gyrus, which is an important part of M1. Since task performance was similar, it is possible that the difference between flexion and extension is rooted in everyday motor requirements. Finger digit extension might not require the same level of specificity during daily motor actions as finger digit flexion. Especially during grasping finger flexion requires detailed motor coordination, whereas the opposite, letting go of something, might simply not call upon the same level of neural specificity, which may be reflected by a somewhat equivocal activity pattern during finger extension. Similar differences between flexion and extension for daily motor requirements have also been suggested in the context of finger digit enslavement (Yu et al., 2010). Secondly, pRF sizes were larger for finger digit extension compared to finger digit flexion. Larger pRF sizes during finger digit extension were most notable on the postcentral gyrus (S1), which is involved in proprioception and relevant for guiding precise finger movements (Todorov and Jordan, 2002). This finding indicates that neuronal populations in the hand area receive feedback from more finger digits during finger digit extension compared to flexion, and is therefore relatively unspecific. The difference in pRF size, thus, also points towards differences in required specificity between finger digit flexion and extension.
4.5. Study limitations
The current study has several limitations. Despite the presented evidence for a detailed within-limb somatotopic organizations of finger digits in sensorimotor cortex, some neuronal populations displayed finger digit representations that appeared out of place with respect to the overall somatotopy. These misplaced representations were mostly located at the extremities of the somatotopic gradient, where either thumb or little finger digit representations were expected. Although it is possible that these misplaced representations are genuine, it may also have resulted from the current task design. Participants flexed or extended the fingers one by one in a sequential fashion either starting from the thumb or the little finger. Activity following thumb and little finger movement might therefore be enhanced by being the first in a sequence of movements, which in turn might increase activity of neuronal populations that do not specifically have these digits as their center digit, but are sensitive to these digits as part of their receptive fields. The Gaussian pRF procedure could then mistakenly attribute an incorrect center finger digit to a neuronal population. Another limitation is the limited number of body part movements that were measured. The current procedure defines Gaussian pRF properties of neuronal populations on the basis of functional activity. However, the only tested functions were the movements of the 5 finger digits. Possibly, numerous neuronal populations have preferred body parts that lie outside the range of finger digits. Since movements of body parts other than the fingers were not tested, the model cannot account for their cortical representations. As a consequence, several currently presented pRF fits might actually be primarily involved in the movement of other body parts or even the hand in total without favoring any of the finger digits in particular. In such scenario’s, the pRF fitting algorithm would converge on the finger digit closest to the actual neuronal population’s preferred body part. Additionally, for neuronal populations, displaying equivocal activity patterns with no clearly distinguishable preferred finger digit, the current pRF fitting algorithm might converge on the middle body part, thereby possibly overestimating the middle finger representation. Further investigation is needed to unravel the full receptive field somatotopy of sensorimotor cortex.
5. Conclusions
Using the population Receptive Field approach we have been able to reveal the detailed somatotopic organization of the primary motor cortex, M1, during finger movements. All individual finger digits are represented within the hand area, ranging from the thumb ventrolaterally to the little finger digit dorsomedially. Similar somatotopic organizations have previously been established for the primary somatosensory cortex, S1. The current study confirms these findings and additionally shows that single finger digit representations are connected throughout sensorimotor areas, supporting sensorimotor integration. Additionally, the response or receptive field sizes in M1 and S1 reveal how neuronal populations integrate movements of distinct, but related body parts. The current findings offer new exciting possibilities for neuroscientific investigation of motor control and sensorimotor integration.
Highlights.
We find a detailed within-limb somatotopy of finger digits in primary motor cortex.
Gaussian population receptive field model was used to describe BOLD activity.
Population receptive fields were found to be larger for M1 compared to S1.
Finger digit flexion and extension result in different receptive field profiles.
Acknowledgements
This work was supported by the National Institute of Mental Health of the National Institutes of Health under award number R01MH111417
This work was additionally supported by the following grants:
EU ERC-Advanced, 320708
STW NeuroCIMT, 14906
Footnotes
Author contributions
WS conducted the experiments, did the analyses and wrote the paper.
NP was involved in editing and reviewing the paper.
NR was involved in experiment conceptualization, reviewing of the paper and supervision.
References
- Beisteiner R, Windischberger C, Lanzenberger R, Edward V, Cunnington R, Erdler M, Gartus a, Streibl B, Moser E, Deecke L. Finger somatotopy in human motor cortex. Neuroimage. 2001;13:1016–26. doi: 10.1006/nimg.2000.0737. [DOI] [PubMed] [Google Scholar]
- Besle J, Sánchez-Panchuelo RM, Bowtell R, Francis S, Schluppeck D. Event-related fMRI at 7T reveals overlapping cortical representations for adjacent fingertips in S1 of individual subjects. Hum Brain Mapp. 2014;35:2027–2043. doi: 10.1002/hbm.22310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Branco MP, Freudenburg ZV, Aarnoutse EJ, Bleichner MG, Vansteensel MJ, Ramsey NF. Decoding hand gestures from primary somatosensory cortex using high-density ECoG. Neuroimage. 2017;147:130–142. doi: 10.1016/j.neuroimage.2016.12.004. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Brown aR, Teskey GC. Motor Cortex Is Functionally Organized as a Set of Spatially Distinct Representations for Complex Movements. J Neurosci. 2014;34:13574–13585. doi: 10.1523/JNEUROSCI.2500-14.2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cheney PD, Fetz EE. Comparable patterns of muscle facilitation evoked by individual corticomotoneuronal (CM) cells and by single intracortical microstimuli in primates: evidence for functional groups of CM cells. J Neurophysiol. 1985;53:786–804. doi: 10.1152/jn.1985.53.3.786. [DOI] [PubMed] [Google Scholar]
- d’Avella A, Portone A, Fernandez L, Lacquaniti F. Control of Fast-Reaching Movements by Muscle Synergy Combinations. J Neurosci. 2006;26:7791–7810. doi: 10.1523/JNEUROSCI.0830-06.2006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dale AM, Fischl B, Sereno MI. Cortical surface-based analysis: I. Segmentation and surface reconstruction. Neuroimage. 1999;9:179–194. doi: 10.1006/nimg.1998.0395. [DOI] [PubMed] [Google Scholar]
- Dechent P, Frahm J. Functional somatotopy of finger representations in human primary motor cortex. Hum Brain Mapp. 2003;18:272–83. doi: 10.1002/hbm.10084. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dechent P, Merboldt K-D, Frahm J. Is the human primary motor cortex involved in motor imagery? Cogn Brain Res. 2004;19:138–144. doi: 10.1016/j.cogbrainres.2003.11.012. [DOI] [PubMed] [Google Scholar]
- Destrieux C, Fischl B, Dale A, Halgren E. Automatic parcellation of human cortical gyri and sulci using standard anatomical nomenclature. Neuroimage. 2010;53:1–15. doi: 10.1016/j.neuroimage.2010.06.010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dumoulin SO, Wandell Ba. Population receptive field estimates in human visual cortex. Neuroimage. 2008;39:647–60. doi: 10.1016/j.neuroimage.2007.09.034. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Friston KJ, Frith CD, Turner R, Frackowiak RS. Characterizing evoked hemodynamics with fMRI. Neuroimage. 1995;2:157–165. doi: 10.1006/nimg.1995.1018. [DOI] [PubMed] [Google Scholar]
- Gogtay N, Giedd JN, Lusk L, Hayashi KM, Greenstein D, Vaituzis aC, Nugent TF, Herman DH, Clasen LS, Toga AW, Rapoport JL, et al. Dynamic mapping of human cortical development during childhood through early adulthood. Proc Natl Acad Sci U S A. 2004;101:8174–9. doi: 10.1073/pnas.0402680101. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Graziano MSA, Taylor CSR, Moore T. Complex movements evoked by microstimulation of precentral cortex. Neuron. 2002;34:841–851. doi: 10.1016/S0896-6273(02)00698-0. [DOI] [PubMed] [Google Scholar]
- Graziano MSa, Aflalo TN. Mapping behavioral repertoire onto the cortex. Neuron. 2007;56:239–251. doi: 10.1016/j.neuron.2007.09.013. [DOI] [PubMed] [Google Scholar]
- Harvey BM, Dumoulin SO. The relationship between cortical magnification factor and population receptive field size in human visual cortex: constancies in cortical architecture. J Neurosci. 2011;31:13604–12. doi: 10.1523/JNEUROSCI.2572-11.2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Herculano-Houzel S. The human brain in numbers: a linearly scaled-up primate brain. Front Hum Neurosci. 2009;3:31. doi: 10.3389/neuro.09.031.2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hlustík P, Solodkin a, Gullapalli RP, Noll DC, Small SL. Somatotopy in human primary motor and somatosensory hand representations revisited. Cereb Cortex. 2001;11:312–321. doi: 10.1093/cercor/11.4.312. [DOI] [PubMed] [Google Scholar]
- Ji KP, Bong SK, Choi G, Seung HK, Jay CC, Khang H. Evaluation of the somatotopic organization of corticospinal tracts in the internal capsule and cerebral peduncle: Results of diffusion-tensor MR tractography. Korean J Radiol. 2008;9:191–195. doi: 10.3348/kjr.2008.9.3.191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kakei S, Hoffman DS, Strick PL. Muscle and Movement Representations in the Primary Motor Cortex. Muscle and Movement Representations in the Primary Motor Cortex. Science (80-. ) 1999;2136:1–5. doi: 10.1126/science.285.5436.2136. [DOI] [PubMed] [Google Scholar]
- Khazipov R, Sirota A, Leinekugel X, Holmes GL, Ben-Ari Y, Buzsáki G. Early motor activity drives spindle bursts in the developing somatosensory cortex. Nature. 2004;432:758–61. doi: 10.1038/nature03132. [DOI] [PubMed] [Google Scholar]
- Kikkert S, Kolasinski J, Jbabdi S, Tracey I, Beckmann CF, Berg HJ, Makin TR. Revealing the neural fingerprints of a missing hand. Elife. 2016;5:1–19. doi: 10.7554/eLife.15292. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kolasinski J, Makin TR, Jbabdi S, Clare S, Stagg CJ, Johansen-Berg H. Investigating the Stability of Fine-Grain Digit Somatotopy in Individual Human Participants. J Neurosci. 2016;36:1113–1127. doi: 10.1523/JNEUROSCI.1742-15.2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lent R, Azevedo FAC, Andrade-Moraes CH, Pinto AVO. How many neurons do you have? Some dogmas of quantitative neuroscience under revision. Eur J Neurosci. 2012 doi: 10.1111/j.1460-9568.2011.07923.x. [DOI] [PubMed] [Google Scholar]
- Li Z-M, Dun S, Harkness Da, Brininger TL. Motion enslaving among multiple fingers of the human hand. Motor Control. 2004;8:1–15. doi: 10.1123/mcj.8.1.1. [DOI] [PubMed] [Google Scholar]
- Markwardt CB. Non-linear Least-squares Fitting in IDL with MPFIT. Astron Data Anal Softw Syst XVIII ASP Conf Ser; 2009. p. 251. https://doi.org/citeulike-article-id:4067445. [Google Scholar]
- Martuzzi R, van der Zwaag W, Farthouat J, Gruetter R, Blanke O. Human finger somatotopy in areas 3b, 1, and 2: A 7T fMRI study using a natural stimulus. Hum Brain Mapp. 2014;35:213–226. doi: 10.1002/hbm.22172. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Meier JD, Aflalo TN, Kastner S, Graziano MSa. Complex organization of human primary motor cortex: a high-resolution fMRI study. J Neurophysiol. 2008;100:1800–12. doi: 10.1152/jn.90531.2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nudo RJ, Jenkins WM, Merzenich MM, Prejean T, Grenda R. Neurophysiological correlates of hand preference in primary motor cortex of adult squirrel monkeys. J Neurosci. 1992;12:2918–2947. doi: 10.1523/JNEUROSCI.12-08-02918.1992. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Nudo RJ, Milliken GW, Jenkins WM, Merzenich MM. Use-dependent alterations of movement representations in primary motor cortex of adult squirrel monkeys. J Neurosci. 1996;16:785–807. doi: 10.1523/JNEUROSCI.16-02-00785.1996. https://doi.org/8551360. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Olman CA, Pickett KA, Schallmo MP, Kimberley TJ. Selective BOLD responses to individual finger movement measured with fMRI at 3T. Hum Brain Mapp. 2012;33:1594–1606. doi: 10.1002/hbm.21310. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Penfield W, Boldrey E. Somatic motor and sensory representation in the cerebral cortex of man as studied by electrical stimulation. Brain. 1937;60:389–443. doi: 10.1093/brain/60.4.389. [DOI] [Google Scholar]
- Petersson P, Waldenström A, Fåhraeus C, Schouenborg J. Spontaneous muscle twitches during sleep guide spinal self-organization. Nature. 2003;424:72–75. doi: 10.1038/nature01719. [DOI] [PubMed] [Google Scholar]
- Rathelot J-A, Strick PL. Subdivisions of primary motor cortex based on corticomotoneuronal cells. Proc Natl Acad Sci U S A. 2009;106:918–23. doi: 10.1073/pnas.0808362106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanchez-Panchuelo RM, Besle J, Beckett a, Bowtell R, Schluppeck D, Francis S. Within-Digit Functional Parcellation of Brodmann Areas of the Human Primary Somatosensory Cortex Using Functional Magnetic Resonance Imaging at 7 Tesla. J Neurosci. 2012;32:15815–15822. doi: 10.1523/JNEUROSCI.2501-12.2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sanes JN, Schieber MH. Orderly somatotopy in primary motor cortex: does it exist? Neuroimage. 2001;13:968–974. doi: 10.1006/nimg.2000.0733. [DOI] [PubMed] [Google Scholar]
- Schieber MH. Constraints on Somatotopic Organization in the Primary Motor Cortex. J Neurophysiol. 2001;86:2125–2143. doi: 10.1152/jn.2001.86.5.2125. [DOI] [PubMed] [Google Scholar]
- Scott SH. The computational and neural basis of voluntary motor control and planning. Trends Cogn Sci. 2012;16:541–549. doi: 10.1016/j.tics.2012.09.008. [DOI] [PubMed] [Google Scholar]
- Seo JP, Jang SH. Different characteristics of the corticospinal tract according to the cerebral origin: DTI study. Am J Neuroradiol. 2013;34:1359–1363. doi: 10.3174/ajnr.A3389. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sporns O, Tononi G, Edelman GM. Connectivity and complexity: The relationship between neuroanatomy and brain dynamics. Neural Networks. 2000 doi: 10.1016/S0893-6080(00)00053-8. [DOI] [PubMed] [Google Scholar]
- Ting LH, McKay JL. Neuromechanics of muscle synergies for posture and movement. Curr Opin Neurobiol. 2007;17:622–628. doi: 10.1016/j.conb.2008.01.002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. Efficient computation of optimal actions. Proc Natl Acad Sci U S A. 2009;106:11478–83. doi: 10.1073/pnas.0710743106. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Todorov E. Direct cortical control of muscle activation in voluntary arm movements: a model. Nat Neurosci. 2000;3:391–398. doi: 10.1038/73964. [DOI] [PubMed] [Google Scholar]
- Todorov E, Jordan MI. Optimal feedback control as a theory of motor coordination. Nat Neurosci. 2002;5:1226–1235. doi: 10.1038/nn963. [DOI] [PubMed] [Google Scholar]
- Van de Moortele P-F, Auerbach EJ, Olman C, Yacoub E, Ugurbil K, Moeller S. T1 weighted brain images at 7 Tesla unbiased for proton density, T2* contrast and RF coil receive B1 sensitivity with simultaneous vessel visualization. Neuroimage. 2009;46:432–446. doi: 10.1016/j.neuroimage.2009.02.009.T. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Van Essen DC, Drury Ha, Dickson J, Harwell J, Hanlon D, Anderson CH. An integrated software suite for surface-based analyses of cerebral cortex. J Am Med Inform Assoc. 2001;8:443–59. doi: 10.1136/jamia.2001.0080443. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Verstynen T, Jarbo K, Pathak S, Schneider W. In vivo mapping of microstructural somatotopies in the human corticospinal pathways. J Neurophysiol. 2011;105:336–46. doi: 10.1152/jn.00698.2010. [DOI] [PubMed] [Google Scholar]
- Victor JD, Purpura, Katz E, Mao B. Population encoding of spatial frequency, orientation, and color in macaque V1. J Neurophysiol. 1994;72:2151–66. doi: 10.1152/jn.1994.72.5.2151. [DOI] [PubMed] [Google Scholar]
- Yu WS, van Duinen H, Gandevia SC. Limits to the Control of the Human Thumb and Fingers in Flexion and Extension. J Neurophysiol. 2010;103:278–289. doi: 10.1152/jn.00797.2009. [DOI] [PubMed] [Google Scholar]
- Zeharia N, Hertz U, Flash T, Amedi A. New Whole - Body Sensory - Motor Gradients Revealed Using Phase - Locked Analysis and Verified Using Multivoxel Pattern Analysis and Functional Connectivity. J Neurosci. 2015;35:2845–2859. doi: 10.1523/JNEUROSCI.4246-14.2015. [DOI] [PMC free article] [PubMed] [Google Scholar]