How the Inference of Hierarchical Rules Unfolds Over Time

Abstract

Inductive reasoning, which entails reaching conclusions that are based on but go beyond available evidence, has long been of interest in cognitive science. Nevertheless, knowledge is still lacking as to the specific cognitive processes that underlie inductive reasoning. Here, we shed light on these processes in two ways. First, we characterized the timecourse of inductive reasoning in a rule induction task, using pupil dilation as a moment-by-moment measure of cognitive load. Participants’ patterns of behavior and pupillary responses indicated that they engaged in rule inference, and were surprised when additional evidence violated their inferred rules. Second, we sought to gain insight into how participants represented rules on this task – specifically, whether they would structure the rules hierarchically when possible. We predicted the cognitive load imposed by hierarchical representations, as well as by non-hierarchical, flat ones. We used task-evoked pupil dilation as a metric of cognitive load to infer, based on these predictions, which participants represented rules with flat or hierarchical structures. Participants categorized as representing the rules hierarchically or flat differed in task performance and self-reports of strategy. Hierarchical rule representation was associated with more efficient performance and more pronounced pupillary responses to rule violations on trials that afford a higher-order regularity, but with less efficient performance on trials that do not. Thus, differences in rule representation can be inferred from a physiological measure of cognitive load, and are associated with differences in performance. These results illustrate how pupillometry can provide a window into reasoning as it unfolds over time.

Introduction

Inductive reasoning is a central element of complex human thought, and features prominently in everyday life. Induction is the process of drawing conclusions that go beyond the available evidence, for example completing patterns or anticipating future events (Hume, 2008). Induction is the counterpart of deduction, in which the available evidence precludes all but a single conclusion, like in syllogistic reasoning. Inductive reasoning is crucial for generalizing knowledge, and supports a wide variety of cognitive capacities, including word learning (Xu & Tenenbaum, 2007), categorical reasoning and generalization (Medin & Schaffer, 1978; Trabasso & Bower, 1968), causal reasoning (Griffiths & Tenenbaum, 2005), anticipation and change detection (Nassar et al., 2012; O’Reilly et al., 2013), and creativity (Collins & Koechlin, 2012). Humans exhibit inductive reasoning spontaneously, consistently, and across various domains (for review, see Tenenbaum, Kemp, Griffiths, & Goodman, 2011).

Humans also have the ability to form abstract, hierarchical representations, for example breaking long-term goals into smaller sub-goals, recognizing abstract patterns across patterns, and asserting internal control over cognitive processes (Badre & Frank, 2012; Botvinick, Niv, & Barto, 2009; Collins & Frank, 2013; Collins & Koechlin, 2012; Miller & Cohen, 2001; Ribas-Fernandes et al., 2011). Surprisingly, people often create such structured hierarchical representations, rather than non-structured flat representations, even when a given task is not itself structured hierarchically (Collins, Cavanagh, & Frank, 2014). Hierarchical representations can increase or deteriorate performance compared to flat representations, depending on the structure of the problem, and the applicability of the structure (Badre & Frank, 2012; Botvinick & Weinstein, 2014; Collins et al., 2014; Farashahi, Rowe, Aslami, Lee, & Soltani, 2017; Frank & Badre, 2012).

In the current study, we aimed to investigate the cognitive processes that underly inductive reasoning, i.e., how abstract rules are gleaned from specific evidence, and how new data are treated that either conform with or violate these rules. We aimed to better understand at a mechanistic level how people integrate multiple pieces of information to infer rules and to make predictions. Our task was structured such that the underlying rules could be represented in a hierarchical or in a flat way, with advantages for both, but in different task conditions. We were interested in the processes involved in rule inference, and whether inferred rules would have hierarchical or flat structure.

Inference and Rule-Guided Reasoning

The study of inductive reasoning has been approached from several angles that are complementary to the approach taken in the present study. Bayesian statistics have been employed to study human inductive reasoning by providing a rational framework for how old beliefs should be updated in light of new information (Tenenbaum, Griffiths, & Kemp, 2006; Tenenbaum et al., 2011). More broadly, the Bayesian account describes a multifaceted number of cognitive phenomena, using a small number of fundamental principles from probability theory. Nevertheless, situated at the computational level of analysis (Marr, 1982), i.e., concerned with what abstract goal an organism is trying to achieve, this approach does not speak to the mechanisms underlying inductive reasoning, i.e., how the goal can be achieved. The current study aims to elucidate inductive reasoning at the algorithmic level.

Knowledge about the implementation of rule-guided reasoning in the brain comes from another line of research, which mainly focuses on the underlying brain circuitry. Studies in humans and non-human primates have identified the brain areas that are involved in the storage, retrieval, and application of rules (for reviews, see Bunge, 2004; Bunge & Wallis, 2007). However, in most tasks in this field, rules are explicitly given to experimental subjects, such that the inductive component of rule-guided reasoning remains largely unknown. In addition, most paradigms focus on very simple rules in order to locate brain regions specific to different cognitive components, leaving unknown the neural structures underlying complex, potentially hierarchical rules. More recently, research employing functional magnetic resonance imaging (fMRI) in humans has established that the abstract, higher-level components of hierarchical representations are represented in more anterior regions, and the concrete, lower-level componets are represented in more posterior regions of the brain (Badre & D’Esposito, 2007; Badre & Frank, 2012; Botvinick et al., 2009; Bunge & Zelazo, 2006; Collins & Koechlin, 2012; Koechlin & Summerfield, 2007).

Some of the fMRI studies of rule representation also involve rule inference, shedding some light on the neural structures underlying these processes. In this line of work, computational models describe sequences of computations during hierarchical inductive learning with regard to certain brain areas (Badre & Frank, 2012). Other models have described the process of learning, storing, and retrieving rules (Collins & Koechlin, 2012). Nevertheless, limited by the low temporal resolution of fMRI, these studies did not address the fine-grained temporal dynamics involved in rule inference that are of interest in the current study.

In the present study, we were interested in how rules are inferred and evolve over time as more and more information comes in. To investigate the underlying processes more closely, we measured pupil dilation, an index of the waxing and waning of cognitive effort over time. By collecting pupillometry data while participants performed the inductive reasoning task, we explored how people organize information in working memory as it comes in, whether they recognize regularities and organizing principles, and – if so – whether proactive hypothesis formulation helps them predict subsequent events. Before describing our experimental paradigm, we briefly introduce pupillometry.

Pupil Dilation as a Measure of Cognitive Processing

Pupil dilation has been used as a measure of cognitive and emotional processing for more than a century (Löwenstein, 1920). Under stable lighting conditions, pupil diameters change as a function of the activity of the brain’s locus coeruleus (LC), a small nucleus in the brainstem (Joshi, Li, Kalwani, & Gold, 2016; Rajkowski, Kubiak, & Aston-Jones, 1993). The LC is the only source of cortical norepinephrine (NE) (Sara, 2009), a neuromodulator that crucially influences a wide range of cognitive functions, such as attention, memory, and cognitive control (Robbins & Arnsten, 2009; Sara, 2009). As a result, dynamic, or phasic, changes in pupil diameter in a well-controlled experimental manipulation index fluctuating levels of cognitive effort during task performance (Eckstein, Guerra-Carrillo, Miller Singley, & Bunge, 2017).

Phasic Pupil Dilation: Adaptive Gain and Unexpected Uncertainty

The significance of phasic LC-NE activity has been concisely summarized by Yu and Dayan’s (2005) unexpected-uncertainty theory and Aston-Jones and Cohen’s (2005) adaptive-gain theory. These complementary theories are grounded in computational modeling (Yu & Dayan, 2005) and neurophysiological, animal, and human research (Aston-Jones & Cohen, 2005). The present work builds upon both theories.

The unexpected-uncertainty theory (Yu & Dayan, 2005) postulates that LC-NE activity is elicited when an event falls outside the range of expected variation (i.e., “unexpected uncertainty”). One line of evidence for this theory comes from studies that show phasic pupil dilation in response to so-called “oddball” stimuli, single differing stimuli in a stream of otherwise identical auditory or visual stimuli (Aston-Jones, Rajkowski, Kubiak, & Alexinsky, 1994; Book, Stevens, Pearlson, & Kiehl, 2008; Wetzel, Buttelmann, Schieler, & Widmann, 2016). Typical oddball studies show that participants’ LC-NE system responds to simple events of unexpected uncertainty, such that perceptual oddball stimuli elicit phasic pupillary dilation. More evidence for the unexpected-uncertainty theory comes from recent research, in which participants predict future stimuli based on past stimuli. In these studies, all stimuli differ slightly from each other (expected uncertainty) because they are generated by stochastic rules. Crucially, sometimes the rule itself changes, such that new stimuli deviate wildly from previous ones (unexpected uncertainty). Stimuli of unexpected uncertainty typically elicit the largest pupil dilations in these paradigms (Nassar et al., 2012; O’Reilly et al., 2013; Preuschoff, 2011), suggesting that participants recognized when the rule changed. In the current study, we employed pupillary responses in a similar way, testing whether participants recognized the violation of the underlying rules, and therefore whether participants were able to infer these rules in the first place.

The second prominent theory of LC-NE function, the adaptive-gain theory (Aston-Jones & Cohen, 2005), states that phasic LC activity is modulated by subjects’ current attentional focus and by perceived stimulus relevance (Aston-Jones et al., 1994; Rajkowski, Majczynski, Clayton, & Aston-Jones, 2004; Usher, Cohen, Servan-Schreiber, Rajkowski, & Aston-Jones, 1999). This theory converges with the unexpected-uncertainty theory in predicting pupillary responses to unexpected events such as perceptual oddball stimuli and rule-violating items, because they trigger attentional shifts. The adaptive-gain theory makes the additional prediction that stimuli perceived as irrelevant elicit smaller pupillary responses than stimuli perceived as relevant. We employed this aspect of pupil dilation to test whether participants recognized that some stimuli were irrelevant in the current task – a conclusion that could only be reached based on knowledge about the rules – and therefore whether participants engaged in rule inference.

Pupil Dilation as an Index of Cognitive Load

Another question of interest in the current study, which has largely eluded prior investigation, is whether different ways of representing rules lead to differences in working memory demands, often termed cognitive load. A large body of research indicates that pupils dilate when the load on working memory increases, for example because an experimental subject is presented with items in a memory test, and that pupils constrict when load decreases, usually when the items have been recalled (Beatty, 1982; Johnson, Miller Singley, Peckham, Johnson, & Bunge, 2014; Klingner, Tversky, & Hanrahan, 2011). More generally, pupil diameter scales across task conditions as a function of working memory demands. Here, we used pupil dilation as a measure of cognitive load in order to investigate whether participants represented the inferred rules in a flat or hierarchical way, as we will explain in more detail in the following section.

Research Questions and Hypotheses

To investigate how participants infer and represent rules, we created an experimental paradigm that was inspired by the card game “SET” (Benjamin & Diane, 2003). We will use terminology that has been devised in previous research (Jacob & Hochstein, 2008), although we modified many aspects of the original task.

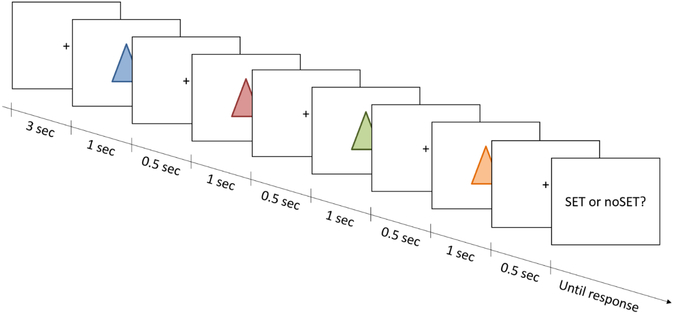
Participants saw four simple items in a row and were then asked to determine whether the items formed a “SET” (Fig. 1). The items varied on three dimensions: color, shape, and fill. Participants needed to decide whether the stimuli fulfilled either of two patterns, “match” or “span”, in each dimension. If all items are identical on a particular dimension (e.g., four red items), they “match” on this dimension. If each item differs from each other (e.g., red, green, blue, and orange), they “span” in that dimension. Items need to adhere to either the match or the span pattern for each of the three dimensions to form a SET. If items violate both patterns in at least one dimension (e.g., three red and one green), they cannot be a SET.

Fig. 1.

Task procedure. Participants saw four items sequentially (1 second each), interleaved by shorter fixation periods (500 milliseconds each). After the last fixation period, the response prompt was shown until a response was given (time-out after 10 seconds). The next trial’s initial 3-second fixation period started after the response or timeout.

The SET rules are hierarchical in that they define a pattern over patterns – i.e., they encompass a description at two different levels of abstraction. The lower-level description defines the patterns ‘match’ and ‘span’ as specific relations among item dimensions. The higher-level description defines valid SET trials as the combination of these patterns across items.

Half of the trials in this task contained a single item that violated the SET rules (Fig. 2). For a participant who has inferred the rule underlying a given trial, a rule-violating item constitutes an event of unexpected uncertainty because the underlying rule changes (Yu & Dayan, 2005), and should violate expectations (Aston-Jones & Cohen, 2005), as explained above. We therefore predicted that rule-violating items would elicit phasic pupillary responses if participants had inferred the underlying rule of a trial. If participants had not inferred the underlying rule, on the other hand, rule-violating items should not elicit larger pupillary responses than other items. The existence of a pupillary response for rule-violating items would therefore provide evidence that participants inferred trial-specific rules.

Fig. 2.

Example SET and noSET trials of different spans. Each cell in the table corresponds to one example trial. Columns vary along span, and rows compare SET to noSET-3 and noSET-4 trials. The small tables in each cell show which patterns (match or span) were fulfilled or violated in each example (check mark versus cross). On SET trials (top row), each dimension fulfills either the match or the span pattern. On noSET trials (middle and bottom rows), one rule-congruent item (third: middle row; or fourth: bottom row) is replaced by a rule-violating item, which violates patterns on two dimensions. The span of a trial determines how many dimensions follow the span pattern – the remaining dimensions match.

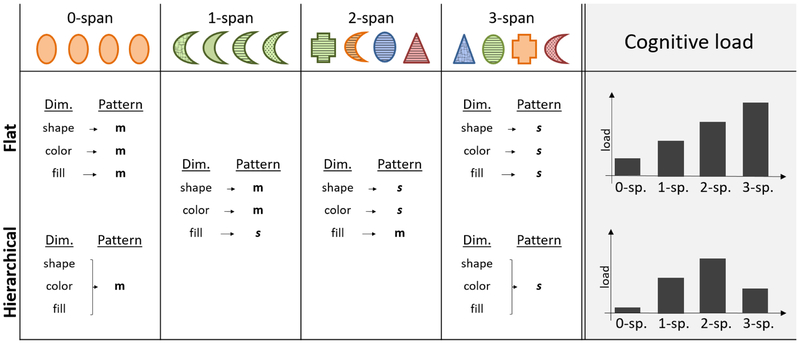
Trials also varied in terms of how many item dimensions spanned and matched. This allowed us to assess whether participants represented rules in a flat or hierarchical way. Trials spanned on 0, 1, 2, or 3 dimensions (matching on the remaining 3, 2, 1, or 0 dimensions, respectively), and will be referred to as 0-span, 1-span, 2-span, and 3-span, respectively. The 3-span condition is characterized by its higher-order regularity: it affords a more efficient summary representation under a hierarchical rule (e.g., “all dimensions span” instead of “color spans, shape spans, and fill spans”). The 1-span and 2-span conditions, on the other hand, do not have such higher-level regularity. Even though it might be possible to form partially hierarchical representations (e.g., “two dimensions span, but ones matches”), we hypothesize that the hierarchy would be most salient, and most likely to be discovered and employed, in the 3-span condition. These differences in cognitive demand between hierarchical and flat rules should be reflected in pupil dilation, therefore allowing us to characterize participants’ rule representation based on their pupillary reponse (Fig. 3; see methods for details).

Fig. 3.

Cognitive load of flat and hierarchical rules. The header row shows example trials of each span category. The table below shows for each example which dimension fulfills which pattern (m: match; s: span). In a flat rule (upper row), all patterns are treated separately, signified by separate arrows pointing from dimensions to patterns. In a hierarchical rule (bottom row), higher-order regularities are recognized and employed for a more efficient representation, such that a single arrow connects all three dimensions to the same pattern in 0- and 3-span trials. 1- and 2-span trials do not have a higher-order regularity, and a flat representation, retaining the information of each feature, is necessary for accurate performance. The right-most column shows the expected cognitive load for each span under a flat versus hierarchical rule. Differences between span conditions arise because the span pattern is more complex than the match pattern (1-sp.: 1-span; 2-sp.: 2-span; etc.).

Methods

Participants

Sixty-eight participants (45 women and 23 men) between 18 and 32 years of age (mean = 21.5, sd = 2.5) were tested in this paradigm. The participants were university students recruited from the UC Berkeley Research Participation Pool (RPP) and received course credit for their participation. Six participants were excluded from all analyses because no reliable pupil dilation data could be collected (less than 30% successful pupil measurements). Possible reasons for this include the specific form and color of eyelashes and iris, excessive blinking, or failure to fixate on the screen (Holmqvist et al., 2011). Eight more participants were excluded because they performed at chance levels on at least one span condition, as indicated by a d’ value of 0.51 or lower in this condition (see methods for details), resulting in a total sample size of 54 participants.

Eyetracking Apparatus

Stimuli were presented using the Tobii E-Prime Software Extensions (Psychology Software Tools, Pittsburgh, PA), which synchronizes the timing of stimulus presentation on the eyetracker with a second computer that records the data. Participants were seated comfortably in front of a Tobii T120 Eye Tracker (17-inch monitor, 1280 × 1024 pixel resolution). Distance to the eyetracker was within a range of 50–80 cm. Pupil dilation data were recorded every 16.6 ms, resulting in a temporal resolution of 60 Hz. Because Tobii T120 automatically compensates for small head movements (within a 30 × 22 cm area at 70 cm distance), participants' heads were not restrained. The camera simultaneously recorded the pupil diameters of the left and right eyes.

Experimental Procedure

Participants completed the study in one visit lasting 45-60 minutes, after providing informed consent. The research assistant explained the eyetracking procedure and answered any questions. Then, participants underwent a standard Tobii 9-point calibration procedure on the eyetracker, which adjusts measurements individually. Participants then underwent a 3-minute baseline assessment of pupil diameter, while fixating a cross-hair on the computer screen. Afterwards, participants completed the SET task during 20-25 minutes, while pupils were recorded. After the task, participants answered a 7-item questionnaire mainly in multiple-choice format that assessed aspects of strategy use in the SET task (see Appendix). Finally, participants completed two standard cognitive assessments: Digit Span (Wechsler & Matarazzo, 1972), a measure of working memory capacity, and Analysis Synthesis (Woodcock, McGrew, & Mather, 2001), a measure of fluid reasoning that requires rule induction. A subset of 30 participants completed the Number Series test (Woodcock et al., 2001) instead of Analysis Synthesis.

The SET task

Task procedure.

Experimenters explained the rules of the game using standardized computerized instructions, and participants were encouraged to ask questions. Participants then completed twelve practice trials of the game with feedback (e.g., “Correct! This was a SET!” or “Incorrect! This was not a SET!”). After additional time for questions and the possibility to re-read the instructions, participants completed two blocks of 40 trials without feedback, separated by a self-paced break. Trial order was randomized within blocks.

Specifics about noSET trials.

In half of the noSET trials, item3 violated the rule (“noSET-3” condition; Fig. 2, middle row), and in the other half, item4 violated the rule (“noSET-4”; Fig. 2, bottom row). Rule-violating items were never presented before the third item so that participants had the possibility to infer rules before encountering a rule-violating item. Each rule-violating item violated the rule on exactly two of the three item dimensions (e.g., color and shape). In 1- and 2- span trials, one matching and one spanning dimension was always violated, rather than two matching or two spanning dimensions. Therefore, throughout the experiment, equal numbers of match and span patterns were violated.

noSET-3 and noSET-4 trials.

The 80 trials of the task were distributed equally among span conditions, resulting in 10 trials for each span on SET trials, and five trials for each span for noSET-3 and noSET-4 trials.

Complexity of span and match patterns.

Based on Boolean complexity (Feldman, 2000), the span pattern is more complex than the match pattern. Specifically, the shortest possible formal expression is longer for span than for match (match: f_Item1 == f_Item2 ∧ f_Item2 == f_item3 ∧ f_item3 == f_item4; Span: ¬(f_Item1 == f_Item2) ∧ ¬(f_Item1 == f_item3)∧ ¬(f_Item1 == f_item4)∧ ¬(f_Item2 == f_item3) ∧¬(f_Item2 == f_item4) ∧ ¬(f_item3 == f_item4), for dimensions fε {color, shape, fill}; match has a length of 6, span has a length of 12). In addition, four different features are imposed on participants’ working memory for each span, whereas the same feature is repeated four times for a match. This implies that working memory load, and therefore pupil dilation, is larger for the span compared to the match pattern. This is a pre-condition for our predictions about differences between flat and hierarchical rule representation.

Cognitive load of flat versus hierarchical rules.

In the case of flat rule representation, each rule consists of three independent parts, corresponding to the three dimensions of the stimuli. Lacking higher-order structure, these three parts need to be stored independently in working memory, and their individual load sums up to determine overall working memory load. Because the span rule is more complex than the match rule, working memory load should increase linearly with span. The top row of Fig. 3 shows the predicted working memory load for each span condition under a flat rule representation.

A different pattern of cognitive load is expected in the case of hierarchical rule representation. Representing rules hierarchically on 3-span trials should reduce the working memory load because they can be summarized as a single rule – namely, that all dimensions span. Compressing 1- and 2-span conditions using partially hierarchical rules, on the other hand, would lead to errors. Taken together, a hierarchical rule representation should reduce the working memory load of 3-span rules relative to 1- and 2-span. The bottom row of Fig. 3 shows the predicted working memory load for the rules in each span condition, given a hierarchical representation. The total cognitive load of each trial as a function of span should therefore reflect the combination of two components: 1) the working memory load of the rule (varying either linearly or in an inverse-U fashion, depending on the rule) and 2) the number of stimulus features that constitute each trial (increasing linearly with span).

Visual features.

All stimuli were equated on luminance to reduce visual confounds to the pupillary response. Item features were not related to an item’s position in a trial, or to its violating the rule or not.

Additional Cognitive Measures

As described below, some participants’ pupillary response profiles were consistent with flat rule representation and others with hierarchical representation. Thus, we sought to determine whether individual differences in rule representation were associated with differences in cognitive performance on independent cognitive assessments. We hypothesized that fluid reasoning would facilitate the discovery of hierarchical rule structure, whereas working memory capacity would facilitate the representation of several independent sub-rules. Thus, we predicted that participants with pupillary evidence for hierarchical rule representation would show higher scores on a standardized measure of fluid reasoning, whereas participants with linear rule representation would show higher scores on a standardized measure of working memory maintenance. We assessed participants’ cognitive abilities with three standardized psychological tests, the digit span task from the Wechsler intelligence test (Wechsler & Matarazzo, 1972), and the Analysis Synthesis and Number Series tests from the Woodcock & Johnson tests of cognitive abilities (Woodcock et al., 2001). The digit span task assesses participants’ short-term memory and working memory capacity; the Analysis Synthesis and Number Series tests assess fluid reasoning abilities. For a more detailed description of these measures, refer to (Johnson et al., 2014).

Analytic Approach

Analysis of Performance Data

We analyzed response times (RTs) and errors with mixed-effects regression models, using R’s package lme4 (Bates, Mächler, Bolker, & Walker, 2015; R Core Team, 2016). The lme4 package allows for the specification of fixed and random effects in hierarchical models of conditions nested within subjects. We modeled effects of interest (e.g., span) both as fixed and random effects for a stringent analysis that allows for between-participant variation in addition to pupilation-wide variation (e.g., “errors ~ span + (span ǀ participant)”). We used the lmer() function to define linear regression models on log-transformed RTs, and the glmer() function to define logistic regression models on the binary error measure (correct/incorrect). We specified linear and quadratic contrasts within the predictor span to assess whether span had linear and/or quadratic (i.e., inverse-U) effects on performance. In order to obtain the correct number of contrasts for the number of levels in the predictor variable span (4 levels), we specified a third orthogonal contrasts (cubic); however, we did not predict a cubic effect of span.

We also conducted post-hoc and planned t-tests. The post-hoc tests were adjusted for multiple comparisons using Bonferroni’s correction. For samples of unequal variances and/or unequal sample sizes, we adjusted the degrees of freedom (df) according to Welch (R Core Team, 2016). The analyses outlined above were conducted on 54 participants. Eight participants with insufficient performance had been excluded, per the following procedure. We first determined a d’ value of performance slightly above chance, a value of 0.51. This corresponds to a hit rate of 6 out of the 10 presented trials per span and a correct rejection rate of 6 out of 10 trials. We then excluded all participants who showed a d’ value below 0.51 in any span condition. Using this procedure, we made sure all participants were excluded who performed at chance, even when they were strongly biased in their overall response pattern, i.e., could not have been eliminated based on hit rate, correct rejection rate, or overall accuracy. In the calculation of d’, we corrected percentages of 100% to 99% (and 0% to 1%) for numerical reasons. Perfect task performance, i.e., 100% hit rate and 100% correct rejection rate, then corresponded to a d’ value of 3.29; exactly reversed responses, i.e., 0% hit rate and 0% correct rejection rate, corresponded to a d’ value of −3.29; chance performance, i.e, 50% hit rate and 50% correct rejection rate, corresponds to a d’ value of 0.

Analysis of Pupil Dilation Data

We first preprocessed raw pupil dilation data. We averaged left and right pupil diameters, then identified and removed measurement errors, using a local loess regression model (loess model; Cleveland, Grosse, & Shyu, 1992). We excluded data points that fell more than five standard deviations outside the local mean, based on 80 consecutive timepoint (1,333 ms). We used the same loess model to interpolate small gaps of missing data (less than 416 ms, i.e., 25 consecutive data points).

The loess regression fits a smooth curve to the data, rather than a straight line. Our procedure is more sensitive to erroneous data points than standard procedures based on experiment-wide exclusion criteria because data points in the timecourse are classified as outliers based on their immediate vicinity. In addition, interpolation of missing data is less susceptible to measurement errors at the edges of missing segments because multiple data points on each side of missing segments are used to calculate the model. Twelve percent of data points were removed during this procedure. Visual inspection confirmed that the majority of excluded data points were outliers. Twenty percent of missing values were then interpolated. Visual inspection confirmed that the interpolated values completed the timecourses naturally.

After cleaning and interpolation, pupil data were down-sampled to 20 Hz using a rolling average of 100 ms and subsequently smoothed using a 5-point smoother. The down-sampling was done to reduce the computational power necessary for statistical analyses on the pupil data. The resulting temporal resolution of 20 Hz was sufficient to test all our hypotheses. Each trial had a duration of nine seconds, resulting in 180 data points per trial.

After preprocessing, we calculated the task-evoked pupil response (TEPR), a standard measure for pupil dilation timecourses. The TEPR represents the increase or decrease in pupil diameter from a trial-specific baseline. We used the average dilation during the first 200 ms of each trial as baseline. Therefore, the TEPR is a timeseries of pupil dilation that is corrected on a trial-by-trial basis for initial pupil diameter. Different task conditions (e.g., SET versus noSET trials) can be compared qualitatively by assessing the TEPR timecourses, but we refrained from statistical tests to avoid problems of multiple comparisons.

To quantify the observed patterns, we calculated a summary measure that reflects the amount of pupil dilation evoked by each individual item in a trial, i.e., an item-evoked pupillary response (IEPR). Assessing IEPRs allowed us to compare the pupillary effects of the presentation of specific items to each other (e.g., rule-violating versus rule-congruent items). Similarly to the TEPR, the IEPR represents the increase or decrease in pupil diameter from an item-specific baseline period to a period capturing the pupillary response to the item. This metric was calculated as the difference in pupil diameter between average pre-item and post-item fixation periods (500 ms). For example, the IEPR of item3 is based on the average pupil diameter during the fixation period following the presentation of item2 (baseline) and the fixation period following the presentation of item3 (item-specific dilation). Calculating the IEPR based on the pupil dilation during the fixation periods rather than during the presentation of the items of interest has two major advantages. First, visual stimulation is identical during the baseline and item-specific time windows (a fixation crosshair), eliminating potential visual confounds. Second, pupils reach peak dilation 1-1.5 seconds after the onset of a visual stimulus (Loewenfeld & Lowenstein, 1993). Because items are presented for 1sec and fixation periods for 500ms, fixation periods therefore coincide with the expected maximum dilation elicted by the item of interest.

To test whether individual participants inferred flat or hierarchical rules, we characterized their pupil dilation patterns as either linear or inverse-U (see Fig. 3). As explained above, we reasoned that if participants inferred flat rules, cognitive load should increase linearly from 0- to 3-span, reflected in a linear increase in pupil dilation. If participants inferred hierarchical rules, on the other hand, cognitive load and span should show an inverse-U relationship. To characterize participants’ inferred rules, we therefore analyzed the linear and quadratic (i.e., inverse-U) components of pupil dilation.

We used regression models to achieve this, predicting pupil dilation during the last three items in SET trials from linear and quadratic span contrasts. As before, we also included cubic contrasts, as well as trial index and timepoint within the trial, as regressors of no interest. We chose the time window of the last three items because only then do participants have enough information to reason about the rules of a trial. A separate regression model was calculated for each participant, revealing the weights of the linear and quadratic components. We calculated a continuous score of pupil dilation pattern for each participant by subtracting the negative quadratic component from the linear component.

To allow for group comparisons, we split participants into two separate groups based on the continuous pupil dilation pattern score. We first focused on the 43 participants whose differential pupil dilation score was predominantly inverse-U or linear, depending on whether their negative quadratic or linear component was relatively larger (a difference score of greater than 0.03), respectively. We selected the cut-off of 0.03 based on the distribution of continuous pupil dilation scores across the full sample, as there were clear peaks in the distribution histograms. This approach yielded 19 participants in the inverse-U group, and 24 in the linear group.

Results

Task Performance

We began by testing for differences in accuracy and RTs as a function of span and SET status (i.e., SET vs. noSET trials). We first analyzed the effects of SET status and span on error rates. There was a strong linear effect of span, such that error rates increased linearly with span, log odds=1.78, z=5.79, p<0.001. There was no main effect of SET status, showing that SET and noSET trials did not differ in overall accuracy, log odds=0.11, z=0.76, p=0.45. Nevertheless, span and SET status interacted marginally for the linear contrast, log odds=0.36, z=1.84, p=0.066, suggesting that span affected SET and noSET trials differently (see Suppl. table 1 for remaining statistics).

We followed up on these analyses with pairwise Bonferroni-corrected t-tests. On SET trials, the tests revealed significant differences between 0-span and 2-span, 0-span and 3-span, and 1-span and 3-span trials (Fig. 4; all ts > 2.64, all ps < 0.032), highlighting the strength of the linear effect of span on performance. On noSET trials, on the other hand, only 3-span trials differed from the other spans (all ts > 4.21, all ps < 0.001; difference between other spans: all ts < 0.99, all ps > .99). To conclude, error rates increased linearly with span on SET trials. On noSET trials, accuracy was similar across spans, with the exception of very high error rates (13.8%) on 3-span trials.

Fig. 4.

Task performance. Shown are mean error rates and RTs for SET and noSET trials of all spans. Error bars represent the standard error of the mean. RTs for correct trials only. 0sp: 0-span; 1sp: 1-span; etc. Statistical comparisons refer to pairwise Bonferroni-corrected t-tests; ~ indicates p < 0.1; * indicates p < 0.05; ** indicates p < 0.01; *** indicates p < 0.001.

We then performed similar tests on RTs. A main effect of SET status, β=0.041, t(54)=2.81, p=0.0070, showed that participants responded faster on noSET than SET trials. A linear effect of span revealed that performance decreased linearly with span, similar to what we found for error rates. An interaction between SET status and the linear span contrast, β=0.069, t=3.10, p=0.0019, revealed that span affected RTs more strongly on SET than noSET trials. Post-hoc t-tests confirmed these results. For SET, 3-span trials differed significantly from 0-span and 1-span trials (both ts > 3.21, both ps < 0.0052) (Fig. 4b). For noSET, there were no differences between spans (all ts < 1.42, all ps > 0.92). In summary, RTs were slower overall and were affected more strongly by span on SET than noSET trials. Notably,we found that RTs and error rates showed similar patterns (Fig. 4), i.e., performance on both measures decreased in the same task conditions. In other words, there was no evidence for a speed-accuracy trade-off on the population level.

Lastly, we tested whether performance differed when rule-violating items were presented at the third or fourth position on noSET trials. In 0-span trials, neither error rates, t(53)=0.50, p=0.62, nor RTs differed, t(53)=0.84, p=0.40, as revealed by repeated-measures t-tests. In higher-span trials, on the other hand, both error rates, t(161)=4.23, p<0.001, and RTs showed differences, t(161)=2.75, p=0.0066, such that participants made more errors and responded slower when rule-violating items were presented at the fourth than at the third position (average of 10.5% versus 5.8% errors; and 527 ms versus 442 ms in RTs). This suggests that rule-violating items imposed additional difficulties when presented at the fourth position.

Pupil Dilation in Response to Rule-Violating Items

Next, we used pupil dilation to assess how participants processed rule-violating compared to rule-congruent items. Because 0-span trials can be solved by identifying perceptual oddball stimuli rather than engaging in rule inference, we analyzed these trials separately. We first present a qualitative assessment of the TEPR timeseries (Fig. 5), and then a quantitative analysis of IEPRs, a summary statistic of item-evoked pupil dilation (Fig. 6).

Fig. 5.

Pupil dilation during trials with and without rule-violating items (correct trials only). 0-span trials are on the left, higher-span trials (1-, 2-, and 3-span) on the right. SET trials (no rule-violating item) are in gray, noSET-3 (item3 violates the rules) in orange, and noSET-4 (item4 violates the rules) in red. Shown are mean pupil dilation (dots) and standard errors of the mean pupil dilation (shaded areas) at each timepoint. The plot also indicates the timing of trial events. Fixation periods (Fix.) are underlied gray and item presentation periods white (It1: item1, It2: item2, etc.). The thick vertical black line indicates the onset of the response prompt (Resp.). Average RTs for each condition are shown within the small black box. Refer to Fig. 6 for statistical analyses.

Fig. 6.

Item-evoked pupil dilation (IEPR) of rule-violating (light gray) and rule-congruent items (dark gray) for item3 and item4. NoS3: noSET-3; NoS4: noSET-4. Also shown are the results of planned, repeated-measures t-tests. * indicates p < 0.05; ** indicates p < 0.01; and *** indicates p< 0.001.

TEPR Timecourses

Perceptual oddball stimuli in our task elicited pupillary violation of expectation, as expected (Aston-Jones & Cohen, 2005; Yu & Dayan, 2005). This was evident in the pupillary responses to rule-violating items in 0-span trials (Fig. 5, left panel). Pupil dilation rose above the baseline level of SET trails (grey) when either item3 (orange) or item4 violated the rule (red). A similar pattern was also evident in higher-span trials (1-, 2-, and 3-span), although in these, rule-violating items were not discriminable based on perceptual features alone. Rule violations at item4 evoked a prominent increase in pupil dilation compared to the SET baseline (Fig. 5, right panel, red). Rule violations at item 3 (orange) were associated with elevated dilation compared to noSET-4 trials, but not SET trials. Both noSET-4 and SET trials can serve as baseline conditions in this case because only rule-congruent items have been presented in both of them up to this point. Overall, the TEPR timecourses suggest that rule violations at item4 elicited considerable pupillary responses in higher-span trials, with less clear evidence at item3. A potential reason for the discrepancy between SET and noSET-4 TEPRs at item3 in higher-span trials is that pupil dilation on SET trials was already elevated at item2, potentially due to random noise that accumulated throughout the 6-second trial. We resolved this issue by assessing the pupil dilation evoked by individual items directly (IEPR), in the analyses below.

In a final observation of the TEPR timecourses of higher-span trials, pupil dilation on noSET-3 trials was reduced relative to SET trials at item4 – i.e., after the presentation of a rule-violating item (Fig. 5, right panel). As explained in the introduction, this suggests that participants perceived items as less relevant that were presented after rule-violating items.

IEPRs and Pupillary Violation of Expectation

We next analyzed the pupillary responses evoked by individual items, i.e., IEPRs. This allowed us to quantify the patterns observed in the TEPR timecourses, and to test the observed patterns statistically. We confirmed that rule-violating items elicited larger IEPRs than rule-congruent items, both on 0-span and higher-span trials, and both when item3 violated the rule (comparing noSET-3 to SET, 0-span: t(55)=4.93, p<0.001; higher-span: t(167)=2.10, p=0.037) and when item4 violated the rule (comparing noSET-4 to SET, 0-span: t(55)=3.88, p<0.001; higher-span: t(166)=4.70, p<0.001) (Fig. 6). Therefore, rule-violating items elicited significant pupillary violation of expectation to conceptual as well as perceptual oddballs, corroborating the patterns observed in Fig. 5.

We next showed that pupillary responses differed when item3 versus item4 violated the rule. Rule violations at item4 were associated with larger IEPRs (0-span: t(55)=2.70, p=0.009; higher-span: t(166)=3.27, p=0.001), suggesting that the violation of expectation was stronger. This result is in line with the behavioral difference presented earlier. We then assessed the decrease in pupil dilation after the presentation of rule-violating items, comparing the IEPR of item4 on SET trials to the IEPRs of item4 in noSET-3 trials. As expected, IEPRs at item4 were reduced in the noSET-3 condition, both for 0-span and higher-span trials (Fig. 6; 0-span: t(55) = 2.24, p = 0.029; higher-span: t(167) = 5.71, p < 0.001). These results indicate that participants expended less cognitive effort on incoming stimuli after rule violations.

Lastly, we compared the patterns of IEPRs between 0-span and higher-span trials. IEPR patterns were strikingly similar, especially for rule-violating items, our main focus of interest (item3, noSET-3, t(103.5)=0.06, p=0.95; item4, noSET-4, t(86.0)=0.92, p=0.36). This shows that similar pupillary violation of expectation was evoked by perceptual and conceptual oddball stimuli. Taken together, the results from the IEPR analysis (Fig. 6) support and extend the observations based on the TEPR timecourses (Fig. 5), and show that participants recognized perceptual as well as conceptual rule violations on-line, i.e., while encoding the items of a trial.

Self-report questionnaire

We followed up these pupillary analyses with participants’ self-report questionnaire. One item on the questionnaire asked participants how likely they were to memorize items that were presented after rule-violating items, on a 5-point scale ranging from “never” (coded as 0) to “always” (4). The group average was 0.92 (SEM: 0.16), with the majority of participants responding either “never” (25 out of 54 participants; 46.3%) or “rarely” (14 out of 54; 26.0%). These results are in line with the pupillary finding suggesting that participants disengaged from items presented after rule-violating items.

Pupil Dilation Pattern and Task Performance

The following section investigates whether participants’ patterns of pupil dilation can shed light on whether they inferred hierarchical or flat rules. To this aim, we calculated a continuous measure of pupil dilation pattern for each participant, which indicates how much pupillary evidence there is for either strategy (Fig. 7B). We then split participants into two separate groups based on this measure (Fig. 7A), after removing participants who showed similar evidence for both strategies. We used the continuous as well as the categorical measure of pupil dilation patterns in all subsequent analyses.

Fig. 7.

The two pupil dilation patterns. A) Average pupil dilation for participants with inverse-U (left; n=19) and linear (right; n=24) pupil dilation patterns on SET trials. Dots indicate means, shaded areas standard errors, shading as in Fig. 5. Bar graph inlays show the mean pupil dilation during the presentation of the final item (5.5-6 sec), to highlight the inverse-U and linear patterns, error bars indicate standard errors. B) Distribution of the continuous measure of pupil dilation pattern (see methods). Dotted vertical line shows the median. Participants with similar evidence for linear and inverse-U patterns (n=11) were assigned to neither group (interval of 0.03 around the median; lightest grey); participants with stronger evidence for one pattern than the other were assigned to the inverse-U (darkest grey) and linear groups (intermediate grey).

Relationship between Pupil Dilation Pattern and Task Approach

As noted previously, humans frequently employ hierarchical structure instead of representing data flat and exhaustively. As such, using hierarchical rules in the current task might be associated with reduced cognitive control, compared to flat rules. We employed the post-task questionnaire to gain insights on this point, asking participants to rate the strategy they had employed on a scale from “relying on [their] gut feeling” to “applying rules consciously” (see Appendix). Participants with inverse-U pupil dilation patterns had lower scores than those with linear pupil dilation patterns, t(37.8)=2.18, p=0.038, in support of this claim. The effect was also evident when pupil dilation pattern was treated as a continuous measure, revealing a marginal correlation with self-reported strategy, r=−0.27, p=0.063.

Reduced cognitive control should also be reflected in reduced RTs. Indeed, on SET trials, continuous pupil dilation pattern had a main effect on RTs in a linear regression model, β=2.54, t(51.6)=2.06, p=0.044. This shows that larger inverse-U components of pupil dilation were associated with faster RTs. The effect failed to reach significance when pupil dilation pattern was treated as a categorical variable, β=0.15, t(2)=1.44, p=0.15, potentially due to imprecise groupings, or because of the reduced power in the categorical compared to the continuous version of the test. There were no RT differences on noSET trials (continuous pupil pattern: β=1.19, t(51.6)=0.34, categorical: β=−0.0015, t(2)=−0.015, p=0.99). Taken together, inverse-U patterns of pupil dilation were associated with a reduced tendency towards “applying rules consciously”, and with faster RTs, suggesting reduced cognitive control.

Linking Inverse-U Pupil Dilation Patterns to Hierarchical Rule Representation

If an inverse-U pattern of pupil dilation indeed reflects the use of a hierarchical strategy, participants with this pattern should show relatively lower performance on trials in which hierarchical rules are maladaptive (1- and 2-span), than in which they are adaptive (3-span) or unnecessary (0-span). We tested this prediction by conducting separate regression models for both pairs of trials, predicting d’ from pupil dilation pattern while controlling for span, d’ was calculated by combining hit rate (accuracy on SET trials) and false alarm rate (error rate on noSET trials) in order to provide an unbiased measure of task performance. Unsurprisingly, span showed at least marginal effects on d’ in all models, all β’8>0.25, all t’s>1.82, all p’s<0.075. Of greater interest, and in accordance with our predictions, pupil dilation pattern showed a significant main effect on d’ on 1- and 2-span trials, such that more linear patterns were associated with better performance (categorical, β=0.64, t(52)=2.46, p=0.017; continuous, β=8.18, t(52)=2.89, p=0.0056), but not on 0- and 3-span trials, revealing similar performance irrespective of pupil dilation pattern (categorical: β=0.12, t(52)=0.59, p=0.56, continuous: β=0.51, t(52)=0.21, p=0.83; Fig. 8A).

Fig. 8.

Task performance of participants with inverse-U and linear pupil dilation patterns. A) d’. Inverse-U patterns were associated with worse performance on 1- and 2-span trials compared to linear patterns, while performance was similar in 0- and 3-span trials. B) The same pattern was evident for SET, but not noSET, trials only (see suppl. Text 2). C) Inverse-U pupil dilation patterns were associated with overall faster RTs on SET trials. This advantage was larger in 0- and 3-span trials compared to 1- and 2-span. D) IEPRs elicited by rule-violating items (average over noSET-3 and noSET-4). Participants with inverse-U pupil dilation patterns showed a U-shaped function, with greater IEPRs for 0- and 3-span trials compared to 1- and 2-span trials.

We next aimed to assess whether a similar pattern would arise for RTs (Fig 8C). Inverse-U pupil dilation patterns were associated with faster RTs on SET trials across all spans, as mentioned in the previous section. Nevertheless, this advantage was more than twice as large in 0- and 3-span trials compared to 1- and 2-span trials, in accordance with our expectations. Thus, on trials in which hierarchical rules were maladaptive, inverse-U patterns of pupil dilation were associated with worse d’ than linear patterns. On trials in which hierarchical rules were adaptive, performance was similar, but inverse-U patterns were associated with an advantage in terms of RTs, highlighting both the advantages and challenges of a hierarchical representation.

Further evidence for the association between inverse-U patterns of pupil dilation and hierarchical strategies comes from participants’ responses to rule-violating items. Behavioral measures (i.e., accuracy, RT) were not sensitive to group differences on noSET trials; however, the pupillary responses were. Participants with inverse-U pupil dilation patterns showed larger IEPRs for rule-violating items in 0- and 3-span compared to 1- and 2-span trials, evident as a quadratic contrast of span on IEPRs in a regression model, β=0.018, t(63)=2.08, p=0.038. Participants with linear pupil dilation patterns, on the other hand, did not show this difference, β=0.011, t(63)=1.33, p=0.19. As predicted, therefore, participants with inverse-U pupil dilation patterns showed increased pupillary responses to rule violations in 0- and 3-span compared to 1- and 2-span trials, i.e., when hierarchical rules were adaptive and could aid in the recognition of rule-violating items, whereas participants with linear patterns did not.

Cognitive test scores

Finally, we compared participants in terms of their scores on standardized cognitive assessments. The two groups did not differ from each other in any measure, as revealed by planned t-tests and Pearson’s correlation (all ps > .43). Thus, pupil dilation patterns were not correlated with performance on standardized cognitive assessments of working memory or fluid reasoning.

Discussion

The goal of the current study was to investigate the cognitive processes underlying rule inference, and the structure of rule representation. To this end, we created a task in which participants would infer rules governing the relations among a series of stimuli, and in which we could alter the structure and complexity of these rules. On each trial of the task, participants had to examine the relationships among four items and determine whether a set of conditions was met such that the items formed a SET. Many possible combinations of items could form a SET, because the items can follow one of two patterns for each of three stimulus dimensions. Thus, the relevant rules differ from trial to trial and need to be inferred anew each time. The four items were presented sequentially, giving participants the opportunity to infer the rules on-line, i.e., while encoding the items, and allowing us to measure the processing of each individual item based on the evoked pupillary response. This combination of pupillometry and behavioral analyses allowed us to infer which strategies participants used to glean governing principles from a series of observations.

Pupil Dilation as a Measure of Working Memory Load and Violation of Expectation

We first verified that pupil dilation was a reliable measure of working memory load (Beatty, 1982; Johnson et al., 2014; Klingner et al., 2011) and violation of expectation (Aston-Jones et al., 1994; Book et al., 2008; Wetzel et al., 2016; Yu & Dayan, 2005) in the current paradigm. The relationship between pupil dilation and working memory load was evident in that pupil dilation ramped up during a trial as one item was presented after another and more information had to be held in memory, and pupil dilation subsided after a response had been made, in a way strikingly similar to classic short-term memory paradigms (Johnson et al., 2014; Klingner et al., 2011). Pupil dilation was also sensitive to violations of expectation, as evident in the TEPR timecourses and IEPRs or rule-violating items in noSET 0-span trials. We were therefore confident in the use of pupil dilation as a measure of working memory load to discriminate between flat and hierarchical rule representations, and as a measure of violation of expectation as evidence for on-line rule inference.

Evidence for Rule Inference

Participants’ pupils showed pronounced violation-of-expectation responses to rule-violating items. In trials other than 0-span, in which the rule-violating item is a simple perceptual oddball, this implies that participants implicitly recognized the violation of an inferred rule. Violation-of-expectation responses were evident as early as at the third position, which suggests that participants inferred rules based on just two items, the minimally necessary information. In addition, violation-of-expectation responses were larger when the fourth item violated the rules rather than the third, and participants also made more errors and responded more slowly on these trials. This pattern suggests that it became increasingly difficult for participants to reject a rule when they had seen more supporting evidence for a it. In other words, participants actively constructed the rule during item presentation, taking into account each item as additional evidence. Finally, participants’ load on working memory was diminished after the presentation of rule-violating items, as evident in reduced pupil dilation. This shows that participants allocated fewer attentional resources once they recognized that an inferred rule was violated, and they had therefore found the correct answer to the trial. Participants confirmed this lack of attention to items after rule-violating items in self-reports. Taken together, participants’ patterns of behavior, combined with their pupillary responses, show that they successfully inferred and employed abstract rules on-line, i.e., while encoding the items.

Flat versus Hierarchical Rule Representation

We next aimed to shed light on the structure of participants’ rule representations, with a specific focus on flat versus hierarchical representation strategies (Badre & Frank, 2012; Collins et al., 2014; Frank & Badre, 2012). In the SET task, exhaustive flat rules retain all the observed information and therefore allow for perfect performance, as long as the amount of information does not exceed working memory capacity. Nevertheless, flat rules do not provide a means to reduce or compress the amount of information through more efficient representation, and therefore individuals representing flat rules have no efficient means of handling trials in which working memory capacity is exceeded. Hierarchical rules, on the other hand, compress information on the basis of higher-order regularities, and restructure information more efficiently. However, hierarchical representation might lead to loss of information when information is not compressible.

Based on the expected working memory load of the rules in each span condition, we first predicted specific patterns of pupil dilation for flat and hierarchical rules: We predicted linear increases in pupil dilation over span for flat rules, and inverse-U relations between span and pupil dilation for hierarchical rules, and characterized participants’ patterns of pupil dilation based on these patterns. Supporting our pupil-based characterization of participants’ rules, participants with predicted hierarchical rules showed faster RTs than participants with predicted flat rules, and reported less conscious effort in representing rules, consistent with the claim that humans prefer to represent rules hierarchically rather than flat, even when it is not necessary or beneficial – and even when it hurts task performance (Badre & Frank, 2012; Collins et al., 2014; Shenhav, Botvinick, & Cohen, 2013). The use of structured hierarchical rules might therefore be a go-to strategy, whereas the use of exhaustive flat rules requires additional cognitive control.

Evidence for the specific benefits, as well as drawbacks, of hierarchical rule representation comes from performance differences between participants in the two groups. We propose that hierarchical rule representation yielded faster responses on 3-span trials because they have higher-order regularity and are compressible, but led to mistakes on 1- and 2-span trials because they lack higher-order regularity, and compression therefore leads to the loss of information.

In noSET trials, the use of hierarchical versus flat rules was not associated with behavioral differences, which was partly due to task design: In these trials, correct answers could be identified seconds before the response prompt. We therefore turned to pupillary responses as a more sensitive measure. Participants with predicted hierarchical rules showed larger pupillary responses to rule-violating items in trials with vs. without hierarchical regularity, suggesting that they had formed stronger expectations and/or were more surprised about the violation of expectations in these trials. This finding again suggests that hierarchical rules were more efficient when processing trials with hierarchical regularity.

The results presented so far held when rule use was treated as a categorical measure (i.e., characterizing participants as using either flat or hierarchical rules) or as a continuous measure (i.e., ranging from predominantly flat to predominantly hierarchical). In contrast to the binary categorical measure, this continuous measure can capture aspects of more flexible rule use. For example, participants might change strategies over time, or employ a mix of strategies. The modulation of performance and pupil dilation patterns by this continuous measure therefore suggests that flexible rule use is reflected in pupillary responses.

We also investigated potential correlates of flat versus hierarchical rule use. One possibility is that the inference of flat versus hierarchical rules challenges different cognitive processes, which are based on different cognitive abilities. However, there were no differences among groups on standard measures of working memory (Forward and Backward Digit Span) or fluid reasoning (inductive reasoning tasks: Analysis-Synthesis and Number-Series). Thus, differences between groups were likely not attributable to differences in the capacity to maintain relevant information in working memory or to integrate relations across multiple stimuli. More research is needed to shed light on potential reasons for individual differences in rule representation.

Ruling out Differences in Decision Threshold as Alternative Explanation

Could there be a simpler explanation for the observed patterns of pupil dilation and task performance than the representation of flat versus hierarchical rules? Previous work that combined pupillometry and drift diffusion modeling points to this possibility. In one study on value-based choice, larger pupil dilations and higher decision thresholds predicted slower but more accurate responses in conditions of cognitive conflict (Cavanagh, Wiecki, Kochar, & Frank, 2014). In our study, 3-span trials are assumed to impose greater cognitive demands than lower-span trials (Fig. 3), suggesting large pupil dilations, high decision thresholds, and slow but accurate responses. Participants with linear pupil patterns indeed showed such a pattern of larger pupil dilations and slower but more accurate responses in 3-span trials, compared to participants with inverse-U patterns. Under the alternative account, one could interpret this pattern to reflect elevated decision thresholds in the face of cognitive demands. The inverse pattern of pupil dilation and performance observed in participants with inverse-U pupil patterns would be interpreted as reduced decision thresholds (Fig. 7 and 8). Intuitively, the alternative account suggests that participants with linear pupil patterns increased their efforts in the face of cognitive demand, whereas participants with inverse-U patterns reduced their efforts, and that this adaptation to task demands is reflected in pupil dilation patterns.

To investigate this alternative account, we estimated decision thresholds by fitting drift diffusion models (see Supplementary Materials for modeling details and statistics). Drift diffusion models estimate drift rates, which reflect the quality of the information available from a stimulus, and decision thresholds, which reflect differences in the criterial amounts of information required before a decision can be made (Ratcliff & McKoon, 2008). Previous research has shown that changes in stimulus difficulty mostly affect drift rate, whereas changes in speed versus accuracy tradeoffs mostly affect decision thresholds (Ratcliff & McKoon, 2008). We thus tested for differences in decision thresholds between participants with linear versus inverse-U patterns of pupil dilation.

Contrary to this alternative account, we found that the groups did not differ in terms of decision thresholds on 3-span trials. Qualitatively, there was also no evidence that participants with linear pupil patterns increased their decision thresholds on 3-span trials, or that participants with inverse-U patterns decreased them. Statistically, we found no evidence that linear pupil patterns were associated with larger increases in decision thresholds for 3-span trials than inverse-U patterns. However, linear pupil patterns were associated with overall higher decision thresholds, which is in accordance with increased cognitive control when representing rules in a flat way. Taken together, these analyses do not support the alternative explanation of our findings that links pupil dilation to decision thresholds rather than working memory load and rule representation.

Conclusion

Using a combination of pupillometry and behavioral analyses, we described the timecourse and nature of rule inference in participants performing a rule-based reasoning task. This research goes beyond previous investigations on rule inference in that it uses a neurophysiogical measure to shed light on the underlying cognitive process. We found that participants inferred rules early and proactively, integrated subsequent information into their rule representation, and recognized rule violations on-line. Patterns of pupil dilation also provided insight into individual differences in the strategies that participants used to represent the rule structure of the task: differences that were not detectable based on behavior alone. In future studies, this novel behavioral and eyetracking paradigm could be used to study changes in cognition over the lifespan or in patient populations.

Appendix

SET Questionnaire

Please answer the following questions.

Please circle the answers that corresponds best to your strategy.

1. Did you use a verbal strategy to remember the items? For example, did you say things in your mind like “red cross, blue moon, orange triangle, …” to remember?

Always used words

Often used words

Sometimes used words

Rarely used words

Never used words

2. Did you rely on your gut feeling when you decided if items formed a SET or not? Or did you consciously apply the rules of the game to decide? Applying the rules would mean going through the presented items’ features and comparing them to each other (“all items were red, so color is the same; there was a triangle, a circle, an oval, and a cross; so shape is different…“).

Always gut feeling

Often gut feeling

Some of both

Often conscious rules

Always conscious rules

3. Did you try to remember all four items before you thought about the solution (at least in most trials)?

Always tried to remember

Often tried to remember

Sometimes tried to remember

Rarely tried to remember

Never tried to remember

4. Did you try to remember the last item in a trial, when you already knew that this would not be a SET? Imagine you saw red-cross, red-cross, and blue-triangle; would you try to remember the next item in this trial?

In this case Always tried to remember last

In this case Often tried to remember last

In this case Sometimes tried to remember last

In this case Rarely tried to remember last

In this case Never tried to remember last

5. Did you concentrate on certain item features when solving the task (e.g. only color or only color and shape) or did you use all of the items’ features (color, shape, and fill for all the items)?

Always concentrated on all three features

Often concentrated on all three features

Sometimes concentrated on all three features

Rarely concentrated on all three features

Never concentrated on all three features

Which feature(s) did you concentrate on?_________________ .