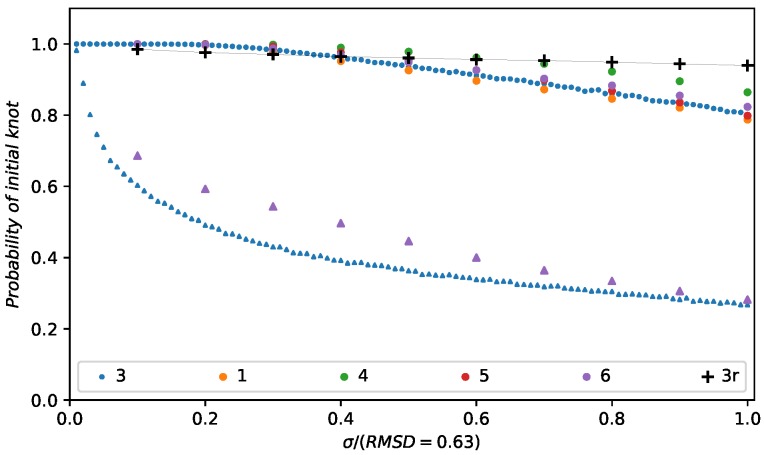
Figure 5.
The stability of a knot against random displacements of its nodes. The probability of a change in topology for random displacements of all nodes belonging to the knots highlighted in Figure 4b is shown. The standard deviation of the random displacements increases on going to the right. While the red trefoil knot indicated by blue disks is stable for rather large displacements, the blue trefoil knot indicated by blue triangles is very unstable. Even small displacements are enough to change the topology. A very similar trend can be observed in model 6, which also exhibits a trefoil knot in the blue region (shown as purple triangles). As with model 3, small perturbations are sufficient to change the topology. All the models show a trefoil in the red region, though. The results for these knots are shown as circles. Here, all knots are stable against the displacements. Additionally, displacements of random regions are shown as black crosses with a connecting line as a guide for the eye (3r). These displacements also do not to change the topology.