Figure 1:

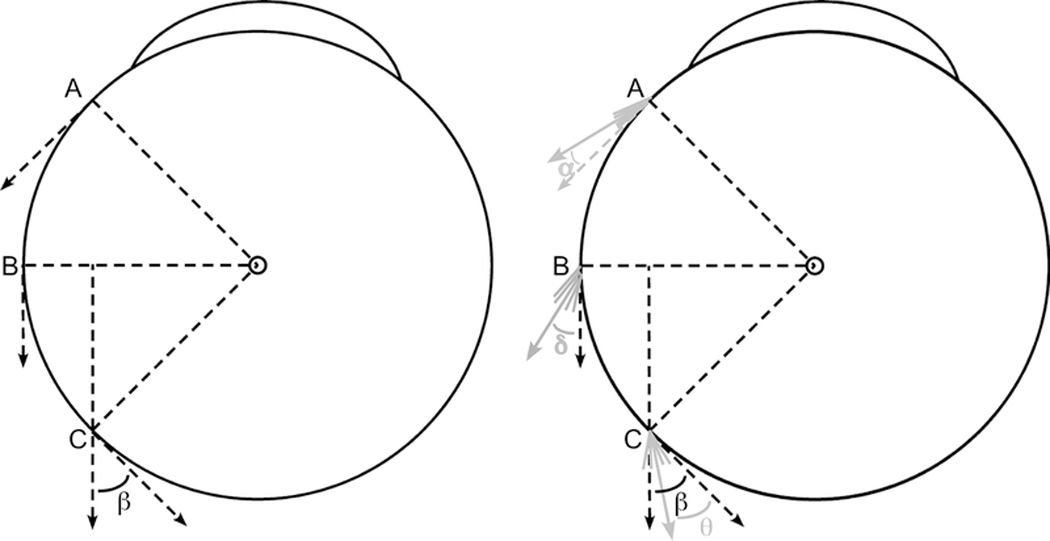
Schematic diagram of the globe-tendon interface. Left) The “arc of contact” biomechanical model assumes infinitely thin extraocular muscle (EOM) tendons and linear muscle paths. As the EOM insertion rotates from point A to the equator (point B), perfect tangency is maintained with 100% force application as oculorotary torque. With further rotation from point B to point C, the posteriorly directed force is no longer tangent to the globe and some rotational torque is lost. The remaining oculorotary torque is proportional to the cosine of angle β. Right) The thickness of the tendon and the changes that occur in the posterior muscle belly during contraction fundamentally alter the globe-tendon interface. Instead of a single line at the EOM insertion, multiple lines are drawn to simulate the muscle fibers that thicken the insertion. At point A, the cumulative force from these lines can be summed into a single force vector displaced by angle α from perfect tangency. From the cosine function, for small angles α, almost 100% of the force exerts oculorotary torque. As the EOM insertion rotates from point A to point B, the muscle thickness increases with EOM contraction, resulting in a larger angle δ displacement from perfect tangency (δ > α). Finally, from point B to point C, imaging demonstrates that the EOM insertion begins to compress the pulley tissue, deforming the EOM path towards the center of the orbit. Thus, despite further thickening of the EOM belly, the resultant angle θ has been shown to be less than the angle β defined by the traditional “arc of contact” model⁷ (θ < β).