The Effects of Sample Size on the Estimation of Regression Mixture Models

Abstract

Regression mixture models are a statistical approach used for estimating heterogeneity in effects. This study investigates the impact of sample size on regression mixture’s ability to produce “stable” results. Monte Carlo simulations and analysis of resamples from an application data set were used to illustrate the types of problems that may occur with small samples in real data sets. The results suggest that (a) when class separation is low, very large sample sizes may be needed to obtain stable results; (b) it may often be necessary to consider a preponderance of evidence in latent class enumeration; (c) regression mixtures with ordinal outcomes result in even more instability; and (d) with small samples, it is possible to obtain spurious results without any clear indication of there being a problem.

The notion that individuals vary in their response to their environment has been well accepted across substantive fields. Leading theories in the behavioral, social, and health sciences emphasize the synergistic role of environmental risk in individual development (Bronfenbrenner, 2005; Elder, 1998; Patterson, DeBaryshe, & Ramsey, 1989; Sampson & Laub, 1993) and consequently the search for differential effects—that is, individual differences in the relationship between a predictor and an outcome—has become of increased salience to applied researchers. Traditional approaches for assessing differential effects involve the inclusion of a multiplicative interaction term into a regression equation. This method is intuitive and useful for testing differential effects which have been hypothesized a priori and involve observed subgroups. An alternative strategy, regression mixture modeling, uses a finite mixture model framework to capture unobserved heterogeneity in the effects of predictors on outcomes (Desarbo, Jedidi, & Sinha, 2001). In other words, regression mixture models are an exploratory approach to finding differential effects that do not require their predictors to be measured (Dyer, Pleck, & McBride, 2012; Van Horn et al., 2009).

This article uses simulations and resamples from applied data to show how sample size affects regression mixture results with the aim of providing users of this method with a starting point for selecting their samples. We aim to show that sample size requirements depend critically on class separation, with regression-parameter estimation and latent-class enumeration being a function of both sample size and class separation.

Methodological Overview

Regression mixture models are a specific form of finite mixture model. The latter term refers to a broad class of statistical models that estimate population heterogeneity through a finite set of empirically derived latent classes. Regression mixture models typically aim to identify discrete differences in the effect of a predictor on an outcome. This differs from other more commonly known mixture approaches, such as growth mixture models (B. O. Muthén, 2006; B. O. Muthén, Collins, & Sayer, 2001; B. O. Muthén et al., 2002) and semiparametric models (Nagin, 2005; Nagin, Farrington, & Moffitt, 1995), in that the latent classes in a regression mixture are defined by between-class differences in the associations between two variables, rather than between-class differences in the means or variances of a single variable (Desarbo et al., 2001; Van Horn et al., 2009; Wedel & Desarbo, 1994). The formulation, estimation, and details around the specification of regression mixtures are already well established (Van Horn et al., 2015). This article focuses on helping users of regression mixtures understand the role that sample size and class separation play in the stability of regression mixture results.

Sample Size in Mixture Models

Sample-size requirements for finite mixture models can be approached from two perspectives. One is the standard question of power: that is, for a given sample size what is the probability that some hypothesis will be rejected, given the population values for all the model parameters? This is a question of obtaining the sampling distribution for a specific parameter, and it can in principle be derived analytically. However, mixture models include many parameters that affect power and attempts at latent-class enumeration typically rely on comparison of penalized information criteria, such as the Bayesian Information Criterion (BIC), for which there is no known sampling distribution. Thus, power for regression mixtures is typically estimated using Monte Carlo simulation. This article raises a second issue related to finite mixtures in general, and regression mixtures in particular. Because mixture models (Bauer & Curran, 2003, 2004) and especially regression mixtures (George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012) rely on strong distributional assumptions for parameter estimation, we aim to show that model results will be increasingly unstable with smaller samples to the point that—even under ideal conditions—such models will yield more extreme results than expected—that is, results far outside the confidence interval suggested by estimated standard errors.

One of the difficulties encountered in estimating finite mixture models in general (without incorporating class-varying regression weights) is that the distribution of each model parameter depends on multiple model- and data-specific factors, including the number of classes estimated, the restrictiveness and complexity of the within-class model, the quality of the covariates, and the reliability of within-class observations (Lubke & Muthén, 2005; MacCallum, Widaman, Zhang, & Hong, 1999; Marcon, 1993; Nylund, Asparauhov, & Muthén, 2007). Moreover, sample-size considerations must take account of class separation, overall sample size, and the within-class sample size. If the estimated proportion of respondents within a given class is small, then a larger overall sample will likely be required to find a stable solution for that class. This makes it challenging to provide a “rule of thumb” for sample size requirements. However, proposing such a rule is not our goal. Rather, this article uses both simulations of selected scenarios and resampling of a real data set to raise researchers’ awareness of the types of problems that regression mixture modeling is likely to encounter when small samples are used; we focus specifically on the interplay between class separation and sample size while also looking at the proportion of subjects in each class.

Much work has looked at latent class enumeration, with some also looking at parameter estimation, with mixture models in general. Of particular note is work which has looked at sample size in factor mixture models (Lubke & Muthén, 2007; Nylund et al., 2007). When looking across the other factors, this work found that class enumeration and parameter estimates were adequate with sample sizes of 500 or less. Few prior studies have examined the effects of sample-size requirements on regression mixture models specifically. Sarstedt and Schwaiger (2008) examined the use of regression mixture models to model market segmentation in the field of marketing, focusing only on the ability of these models to find the true number of latent classes. They found that while the Akaike information criterion (AIC; Akaike, 1973) performed poorly regardless of sample sizes, the consistent Akaike information criterion (CAIC; Bozdogan, 1994) performed well when samples were as small as n = 150 to n = 250. However, Sarstedt and Schwaiger’s study (2008) was focused on situations with very high class separation resulting from large differences across classes in both intercepts and multiple regression weights. Across the different classes effect sizes, measured as R² values ranged from .60 to .98, indicating that in some classes, very little residual variance remained. Effects in the social sciences are generally much smaller; and when one’s interest is in finding differential effects, intercept differences may be small to nonexistent. It should also be noted that Sarstedt and Schwaiger (2008) did not evaluate the precision or stability of parameter estimates.

One other study examined sample size requirements for regression mixtures, this time using a negative binomial model. Park, Lord, and Hart (2010) incorporated design features typically seen in highway crash data into their simulation, examining bias in parameter estimates, and found large bias in the dispersion parameter in samples less than n = 2,000 under realistic conditions. They not only noted unstable solutions with small sample sizes and moderate or low effects but also found that under conditions of high class separation (i.e., large mean differences between classes), their model was stable for samples as small as n = 300. A reason for these discrepant results has to do with how much classes differ; as Park et al. (2010) put it, “the sample size need not be large for well-separated data, but it can be huge for a poorly separated case.” Class separation is at its lowest when differences between latent classes are solely a function of differences in regression weights with no mean differences; and in this case, the multivariate distributions of the data for the different classes overlap almost completely. This is also the point at which regression mixtures fulfill their promise as a method for exploring for differential effects, since they should be capable of finding discrete groups of respondents distinguished primarily by differences in regression weights. The current study is distinct from the two previous simulation studies in that its primary goal is not to provide sample-size requirements but to illustrate the range of problems that may occur in practice when using regression mixtures with small samples and to examine bias in regression parameters.

The Current Study

This study aims to demonstrate the consequences of using regression mixtures as sample sizes decrease. Using both simulations and resampling of a real-world data set, we evaluate the impact of sample size and class balance on latent class enumeration, bias in model parameters, the adequacy of estimated standard errors, and model stability. We are particularly interested in cases where the result of small samples is not low power, but rather parameter estimates which do not represent the population well. Based on the results of previous applied research and simulations, we hypothesize that the use of small samples in regression mixture models will increase the likelihood of extreme results, such that estimates of regression parameters across classes will be biased away from each other, while the confidence intervals of the estimates will be too narrow. Additional analyses focus on the role of class separation in this relationship.

Ordinal logistic regression mixture models have been found effective for evaluating differential effects in the presence of skewed outcomes (Fagan, Van Horn, Hawkins, & Jaki, 2012; George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012). Therefore, we also test the hypothesis that the effects of sample size will be stronger on the ordinal logistic model because less information is available for analyses with ordinal outcomes.

Simulation Study

Method

Five hundred Monte Carlo simulations were run per condition. Because of our interests in the problems that can occur when latent classes are defined solely by differential effects, our initial simulations were for a two-class model where the only parameters that differed between the classes were regression weights and residual variances (more complex models are subsequently evaluated). We only consider two classes for the true model because we want to illustrate the issue in a relatively simple context. The initial simulations used one predictor, X, and one outcome variable, Y. The regression relationship for Class 1 was Y = 0.70X+e, and for Class 2, Y = 0.20X+e. The predictor and the residuals, e, were drawn from a normal distribution with the residuals for Y scaled so that the standard deviation (SD) of Y is 1. Thus, the slope of the predictor is equal to the correlation of X and Y. We specifically chose these regression weights to represent the types of differential effects that we would expect to see in the applied social sciences, and because, we argue that if regression mixtures cannot detect the differences between a small and large correlation then they are not very useful for exploring practically meaningful differential effects. Normal distributions assess the impact of sample size under ideal conditions.

Eighteen simulation conditions were examined. For the first 10 conditions, the total number of individuals in the data set (6,000, 3,000, 1,000, 500, and 200) as well as the proportion of the sample in each class (50% in each class and 75% in Class 1 and 25% in Class 2) was varied. The largest case, 6,000 individuals in total was chosen based on prior studies (e.g., Van Horn et al., 2009; Van Horn et al., 2012) that suggested this was a sufficient number of individuals to find expected results. Conditions 11 to 18 were designed to highlight changes in results as a function of class separation. Conditions 11 to 14 had high class separation with an intercept of 1 or 1.5 for Class 1 in which the effect of X on Y was 0.7. To investigate the parameter recovery under low levels of class separation, we examined regression weights with effects of 0.7 in Class 1 and .40 in Class 2. Conditions 17 and 18, show how the inclusion of an additional predictor affects performance. To show the greatest additional benefit of including other Xs in the model, the additional predictor, X₂, has the same effect on the outcome as the original predictor; it is assumed to be standard normal; and it is uncorrelated with the first predictor (X₁). These additional simulations illustrate that sample size requirements change as a function of different model features, and that general rules of thumb are therefore inadequate.

Data were generated in R (R Core Team, 2016), and the models fit using Mplus version 7 (L. K. Muthén & Muthén, 2008). The true model had two classes, and thus one-, two-, and three-class models were fit to examine how frequently the correct number of classes would be selected based on the BIC and the bootstrap likelihood ratio test (BLRT). However, because of the computational burden, BLRTs were not run for Conditions 11 to 18. We also chose to focus on the BIC because it delivered the most reliable results in previous research with regression mixtures (George, Yang, Van Horn, et al., 2013; Van Horn et al., 2012). Results for the AIC and adjusted Bayesian information criterion (aBIC) were also collected for the ordinal regression mixture model, as these results differed across criteria. The percentage of simulations for which the two-class model would have been selected over the one-class or the three-class model were reported to better understand failures to select the true two-class model; we also calculated the percentage of times the three-class model is chosen over the two-class model; but importantly, we considered failure of the three-class model to converge as indicating support for the two-class result. This decision was based on our previous experience that overparameterized models frequently fail to converge to a replicated log-likelihood (LL) value. This assumption changed results dramatically only for the ordinal outcomes model; class enumeration tables without this assumption are available from the authors on request. Finally, the average size of the smallest class across simulations was recorded for each condition; and when the smallest class is relatively small (e.g., lower than 10% of the overall sample size), it was necessary to give further consideration to whether there was sufficient evidence to support a meaningful additional class, or if the apparent presence of an additional class was due to outliers or violations of the distributional assumption. We note that 10% is an arbitrary number and that it is possible to have true and meaningful classes below this size, given enough information in the data to reliably detect these classes.

All study simulation conditions were evaluated for replicated convergence, model fit, class enumeration, and parameter estimation. Replicated-convergence is defined as a simulation run in which (a) a solution was obtained and (b) the log-likelihood value was replicated to the next integer in at least 2 of the 24 starting values.

Bias in parameter estimates was examined for every replicated solution in which the true two-class model was selected using the BIC. Specifically, we calculated the proportion of individuals in each class, the average across simulations for each parameter estimate and the associated standard error, as well as the parameter coverage, that is, the percentage of simulations for which the true parameter is contained in the 95% confidence interval. Finally, we displayed the distribution of slopes across simulations for conditions with smaller sample sizes. This serves two purposes. First, it helps identify the presence of outliers in the estimated slopes; and, second, it helps assess the robustness of the estimation and underlying sampling distribution. To correct for the problem of label-switching in simulations, classes were sorted such that the class with the stronger effect of X on Y was always Class 1 (McLachlan & Peel, 2000; Sperrin, Jaki, & Wit, 2010). In cases where the two classes were not distinct, as evidenced by the distribution of the parameter estimates, average parameter estimates were somewhat biased in favor of the correct solution because of this class sorting.

Results

Class enumeration. Table 1 shows for each of the first 10 basic conditions the proportion of 500 replications in which the LL value was replicated along with average entropy values across these replications. No problems with model estimation were observed for the one-class model in any conditions, or for the two-class model when sample sizes were moderate to large. However, the two-class model’s rate of convergence to a replicated LL value dropped to around 70% for small sample sizes. In the case of the three-class model, only around 60% of the simulations converged to a replicated LL value when sample sizes were large, and when they were small, replicated convergence rates were as low as 38%. In most cases, nonconvergence was due to the best likelihood value not being replicated, rather than to a failure of convergence for all starting values. Further evaluations with 504 starting values (a multiple of 24, the number of processors available), 96 of which were run to convergence, did not improve the percentage of solutions that replicated the best LL value. This suggests that this problem was largely because of model misspecification, that is, resulted from estimating an incorrect three-class model.

Table 1.

Convergence and Entropy for Each Simulation Condition.

Cond ID	Sample size balanced design	True model sample sizes		Estimated latent class model
		Two classes		One class	Two classes		Three classes
		N 1	N 2	% Cnvrg	Entropy	% Cnvrg	Entropy	% Cnvrg
1	Balanced (50/50 split)	3,000	3,000	100.0	0.11	100.0	0.40	58.2
2		1,500	1,500	100.0	0.14	100.0	0.43	56.8
3		500	500	100.0	0.37	90.2	0.57	50.0
4		250	250	100.0	0.60	77.4	0.69	41.0
5		100	100	100.0	0.75	71.0	0.78	42.2
6	Unbalanced (75/25 split)	4,500	1,500	99.6	0.27	100.0	0.50	57.4
7		2,250	750	98.6	0.28	99.8	0.51	56.4
8		750	250	99.4	0.49	88.2	0.65	51.0
9		375	125	100.0	0.68	74.8	0.74	45.6
10		150	50	100.0	0.79	71.8	0.82	37.6

Note. N₁ is the sample size within Class 1 and N₂ is the sample size in Class 2. The mean entropy across all simulations is reported. % Cnvrg is the percentage of 500 replications which converged to a replicated solution.

The entropy of the two- and three-class results exhibits an interesting pattern with entropy being the lowest for the two-class models with large sample sizes. Low entropy values are typical for regression mixture models (Fagan et al., 2012) and can be expected when classes are poorly separated. Because entropy has been used as a criterion for selecting latent-class models (Ramaswamy, Desarbo, Reibstein, & Robinson, 1993), the true entropy values for our models are worth knowing. More specifically, if the true entropy is lower for the true two-class model, it would suggest that entropy should not be used for regression mixture model selection. Accordingly, we estimated the true entropy for these models using a data set generated from the same population model but with 1,000,000 cases in each class. In these runs, the models with balanced and unbalanced class sizes had entropy values of 0.13 and 0.30, respectively. Differences between the balanced and unbalanced designs can be attributed to the construction of entropy: When the highest posterior probabilities are used, individuals are more likely to be classified as being in the larger class, and since this class represents a larger proportion of the data in an unbalanced design, entropy is also higher. Therefore, we take these numbers as indicating that the conditions with the lowest average entropy estimates (i.e., Conditions 1, 2, 6, and 7) are reasonably well estimated, whereas those with high entropy values (i.e., those with smaller sample sizes) are biased. The results in Table 1 demonstrated two important features of entropy in regression mixture models: (a) that the true models may have the lower values of entropy and (b) that estimates of entropy may be upward biased as sample size decreases and/or if the model is misspecified as having too many classes. While low entropy values do not discredit a model, that is, it can still be effective for finding differential effects in the population—they do suggest that its performance when classifying individuals will be poor.

Our class enumeration results are provided in Table 2. For the basic setup, the BIC criterion usually yielded the correct two-class solution when sample sizes were 3,000 or more (Conditions 1, 2, 6, and 7), but none of the criteria performed well when sample sizes were smaller than that. These analyses also looked at the size of the smallest class for both the two- and three-class solutions and found that the average class size of the smallest class for the three-class solution was always well below 10% of the overall sample size, whereas in all two-class solutions it was more than 10%. In practice it appears that small classes can be an indicator of a spurious class. For these simulations, if an arbitrary criterion of 10% in the smallest class was used to exclude a result, the three-class solution would usually be excluded from consideration. On the whole, these simulations suggest that for samples of 1,000 or more researchers are reasonably likely to arrive at the correct two-class solution for this data-generating scenario if all information is used rather than any one criterion.

Table 2.

Latent Class Enumeration Across Simulations.

Condition ID	Equations of data-generated scenarios	Sample size balance design	True model		Estimated models
					Selecting 2 over 1 and 3 class			Selecting 3 over 2 class
			N 1	N 2	% BIC	% BLRT	Smallest class size	% BIC	% BLRT	Smallest class size
1	Basic regression mixture set-up:  $\mathrm{LC}1:Y=0.2X+e$  $\mathrm{LC}2:Y=0.7X+e$	Balanced	3,000	3,000	99.6	95.2	42.5	0.2	4.5	2.4
2			1,500	1,500	87.6	92.8	39.2	0.2	5.8	2.4
3			500	500	18.2	40.6	26.9	5.4	1.6	2.5
4			250	250	4.8	10.6	17.5	9.7	1.2	2.3
5			100	100	7.2	6.2	12.3	20.3	1.0	3.4
6		Unbalanced	4,500	1,500	96.8	94.6	25.8	0.6	5.4	1.9
7			2,250	750	84.8	91.8	26.6	1.4	7.4	2.3
8			750	250	21.0	42.2	19.8	6.0	3.8	1.8
9			375	125	9.4	16.8	12.5	12.9	2.2	2.1
10			150	50	10.0	10.4	10.5	15.2	1.2	2.9
11	Intercept difference of 1  $\mathrm{LC}1:Y=0+0.2X+e$  $\mathrm{LC}2:Y=1+0.7X+e$	Balanced	250	250	72.8	NA	38.6	1.9	NA	6.5
12		Unbalanced	375	125	86.0	NA	24.7	2.1	NA	4.8
13	Intercept difference of 1.5  $\mathrm{LC}1:Y=0+0.2X+e$  $\mathrm{LC}2:Y=1.5+0.7X+e$	Balanced	250	250	97.9	NA	42.8	0.5	NA	7.0
14		Unbalanced	375	125	98.0	NA	25.6	1.8	NA	5.9
15	Decrease slope differences  $\mathrm{LC}1:Y=0.4X+e$  $\mathrm{LC}2:Y=0.7X+e$	Balanced	1,500	1,500	4.2	NA	25.0	6.7	NA	4.1
16		Unbalanced	2,250	750	7.4	NA	20.6	0.4	NA	3.2
17	Uncorrelated predictors  $\mathrm{LC}1:Y=0.2X_1+0.2X_2+e$  $\mathrm{LC}2:Y=0.7X_1+0.7X_2+e$	Balanced	250	250	98.5	NA	48.2	1.5	NA	8.3
18		Unbalanced	375	125	97.4	NA	25.1	2.6	NA	5.4

Note. % BIC is the percentage of simulations selecting this model using the Bayesian information criteria and BLRT is the bootstrap likelihood ratio test. NA = not applicable. Smallest class size is the average proportion of respondents in the smallest class across all simulations.

We next examined the percentage of the population estimated as being in each class. For Conditions 1 to 5, we expect 50% of the population in each class; but the results showed that on average, when N < 1,000, the model classifies more individuals into the class with the higher regression weight. For Conditions 6 to 10, in which 75% of the individuals in the population were actually in Class 1, the pattern was somewhat different with bias only at sample sizes 200 or 500.

As shown in Table 3, average model parameters were reasonably well estimated for all conditions in Class 1 (with the larger regression weight). However, in Class 2, bias in all parameters increased as sample size or class separation decreased, with class means (intercepts) showing an upward bias, and regression weights and variances showing a downward bias. While some of the model-parameter estimates appeared reasonable even with small samples, the coverage probabilities for the parameter estimates—defined as the percentage of simulations for which the true value is inside the 95% confidence interval—revealed serious problems with estimated confidence intervals as sample size decreased. Note that even in conditions with sample sizes more than 1,000, coverage was slightly less than desirable for the slope parameters. This suggests that estimated standard errors were too small. The very poor coverage estimates observed for sample sizes of 200 and 500—especially for Class 2—could be a function of model instability as some simulations yielded extreme estimates. (Note that, for the residual variances, the 95% confidence interval was not accurate because variances do not follow a t distribution.)

Table 3.

Estimated Parameter Means, Standards Errors, and Coverage Across All Simulations.

	Class 1									Class 2
	Intercept			Slope			Residual variance			Intercept			Slope			Residual variance
Condition	Mean	SE	Cover	Mean	SE	Cover	Mean	SE	Cover	Mean	SE	Cover	Mean	SE	Cover	Mean	SE	Cover
Truth	0.00			0.70			0.51			0.00			0.20			0.96
1	0.00	0.03	0.95	0.70	0.05	0.93	0.50	0.06	0.94	0.00	0.03	0.96	0.20	0.06	0.93	0.96	0.05	0.92
2	0.00	0.04	0.96	0.71	0.06	0.90	0.50	0.08	0.91	0.00	0.05	0.97	0.17	0.09	0.93	0.96	0.07	0.93
3	0.01	0.05	0.89	0.71	0.07	0.77	0.49	0.08	0.67	0.08	0.09	0.84	−0.04	0.13	0.68	0.88	0.12	0.84
4	−0.11	0.05	0.85	0.61	0.05	0.29	0.57	0.06	0.26	0.37	0.06	0.47	−0.69	0.09	0.26	0.49	0.08	0.32
5	0.14	0.05	0.79	0.67	0.06	0.11	0.57	0.06	0.23	0.40	0.06	0.21	−0.77	0.05	0.08	0.22	0.05	0.08
6	0.00	0.02	0.95	0.70	0.03	0.94	0.51	0.03	0.93	0.00	0.05	0.96	0.19	0.10	0.93	0.95	0.08	0.93
7	0.00	0.03	0.96	0.71	0.04	0.95	0.50	0.05	0.94	−0.01	0.07	0.95	0.18	0.14	0.91	0.95	0.11	0.92
8	0.03	0.04	0.88	0.72	0.05	0.76	0.49	0.06	0.76	0.00	0.13	0.80	−0.14	0.18	0.67	0.84	0.17	0.76
9	−0.01	0.04	0.86	0.69	0.05	0.53	0.50	0.05	0.42	0.44	0.11	0.47	−0.31	0.11	0.23	0.49	0.14	0.37
10	0.01	0.05	0.79	0.72	0.05	0.62	0.49	0.05	0.62	0.44	0.04	0.25	−0.48	0.03	0.08	0.15	0.03	0.09
Increased class separation
Truth	1.00			0.70			0.51			0.00			0.20			0.96
11	0.99	0.12	0.88	0.69	0.09	0.84	0.49	0.11	0.86	−0.09	0.21	0.82	0.19	0.11	0.92	0.88	0.16	0.84
12	1.00	0.08	0.92	0.70	0.06	0.89	0.49	0.08	0.90	−0.13	0.29	0.79	0.19	0.15	0.88	0.82	0.21	0.78
Truth	1.50			0.70			0.51			0.00			0.20			0.96
13	1.49	0.11	0.92	0.71	0.08	0.91	0.50	0.10	0.90	−0.02	0.19	0.89	0.19	0.09	0.95	0.93	0.17	0.86
14	1.49	0.07	0.93	0.71	0.05	0.93	0.50	0.07	0.92	−0.02	0.28	0.83	0.20	0.13	0.92	0.91	0.24	0.82
Decreased class separation
Truth	0.00			0.70			0.51			0.00			0.40			0.84
15	0.00	0.06	0.93	0.70	0.08	0.69	0.49	0.10	0.68	−0.03	0.09	0.83	0.23	0.12	0.72	0.71	0.10	0.71
16	−0.01	0.05	0.93	0.72	0.06	0.72	0.48	0.08	0.69	0.00	0.12	0.85	0.22	0.15	0.68	0.68	0.15	0.67

Note. SE = standard error. For simulations where the two-class solution was selected by the Bayesian information criterion (BIC), the median estimated standard error, and the coverage estimate (percentage of simulations for which the 95% confidence interval included the true value) are reported.

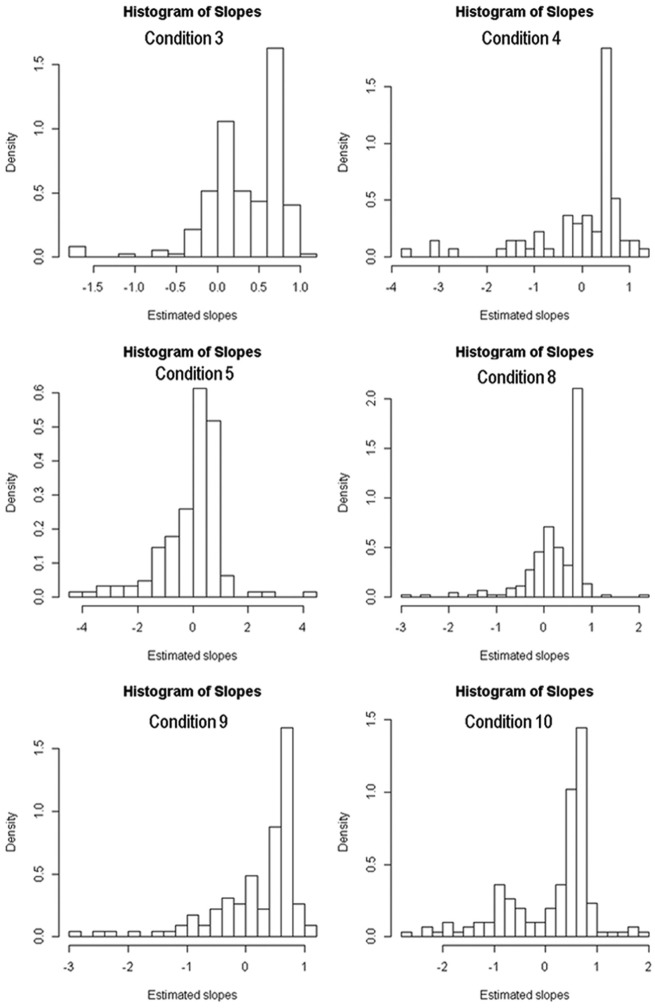
We further investigated model instability by examining the distribution of regression weights across simulations. Figure 1 presents histograms of the slopes for both classes mixed, for the conditions with less than 1,000 observations. The conditions with 3,000 and 6,000 observations (not shown) demonstrated a clear separation between estimated slopes with little evidence of any outlying solution. For smaller samples distribution of the estimated slopes became unimodal suggesting that—across simulations—the parameter estimates for the two classes are not reliably distinguished. Of concern is the appearance of many outliers, which indicates that in many simulations the estimated parameters bear little resemblance to the true values in the population. These graphs should show peaks at 0.2 and 0.7, the true values for the regression weights in each class. These peaks were evident in Conditions 3 and 8, although both conditions feature some extreme outliers. However, at sample sizes of 500 and 200, the two peaks merge into one and there are many outliers, both above and below the true values.

Figure 1.

Histogram of estimated slopes for scenarios with 1,000 or fewer observations.

As sample sizes decrease, we also expect wider confidence intervals and more variation across simulations. However, the extreme results seen in some simulations are not just a function of sampling variability, as the models’ estimated standard errors are still relatively low and some of the parameter estimates are more than 15 standard errors from the true value. We then examined individual results from the small samples that showed extreme values, and found that many of the simulation results with extreme regression weights contained quite small classes that in practice would probably not be considered strong evidence for differential effects. However, it was also not uncommon to find results that featured (a) strong effects in the opposite direction to the true effects with reasonably large class sizes, (b) replicated LL values, and (c) no other evidence that the result was erroneous. Small samples, in other words, could make it extremely difficult to discover that there is a problem with a given finding.

Our next set of simulations focused on how identification of the correct number of classes was affected by class separation. With a sample size of 500 in Condition 4 fewer than 5% of the replications according to the BIC resulted in the correct number of classes being chosen. With increased class separation in Conditions 11 to 14, the proportion of simulations that chose the correct number of classes rose dramatically to more than 70% and 95% when between-class intercept differences were 1 and 1.5, respectively. Conditions 15 and 16 replicated Condition 2 (with 1,500 observations in each group), but with decreased class separation caused by decreasing the differences in the slopes from 0.2 and 0.7 to 0.4 and 0.7; this reduced the proportion of simulations that correctly identified two latent classes from 87.9% to just 4.2%. Finally, in Conditions 17 and 18, (not included in Table 3 because of the additional parameters), we examined the impact of including more information in the regression mixture model by adding an additional predictor. In this condition with a sample size of 500, the BIC found the correct two-class solution in more than 97% of the simulations. Parameter estimates from these models were all reasonable, although coverage rates were somewhat less than 0.95 for the models with strong class separation and far less than 0.95 for models with weaker class separation.

We also investigated the use of an ordinal logistic model for identifying the correct number of classes (Table 4), which was recommended by Van Horn et al. (2012) and George, Yang, Jaki, et al. (2013) as a method for addressing nonnormal errors. As in the normally distributed model, there were substantial issues with model convergence for the two-class ordinal logistic models when the sample size fell below 3,000. Furthermore, even with 6,000 observations (the same number as in George, Yang, Jaki, et al. (2013), the BIC chose the correct two-class model in only 5% of the simulation replications. The main difference between this result and the previously reported results (George, Yang, Jaki, et al., 2013; Van Horn et al., 2012) is that here there was no intercept difference. When we added a between-classes intercept difference of 0.5 SDs, we replicated the previous results, choosing the correct two-class solution in 95% of the simulations. With large sample sizes, the BLRT and aBIC had better, though still inadequate results; in the best-case scenario with a sample of 6,000, the BLRT found two classes in 74% of simulations. Because the correct number of classes was rarely selected, parameter estimates are not reported.

Table 4.

Latent Class Enumeration Across Simulations for the Ordinal Regression Mixture Model.

Balanced design			Estimated models
	True model		Selecting two- over one- and three-class				Selecting three- over two-class				Percentage of runs not converged
	N 1	N 2	% AIC	% BIC	% aBIC	% BLRT	% AIC	% BIC	% aBIC	% BLRT	One-class	Two-class	Three-class
Balanced (50/50 split)	3,000	3,000	76.4	5.0	50.6	73.8	22.8	0.6	0.8	23.2	0.0	1.6	71.6
	1,500	1,500	60.6	4.2	15.0	39.4	24.1	4.2	4.2	23.6	0.0	17.2	71.4
	500	500	42.0	0.4	9.2	18.6	27.4	10.8	12.6	20.6	0.0	32.2	73.0
	250	250	34.8	0.0	15.4	17.6	27.6	14.3	18.9	19.0	0.0	36.2	69.8
	100	100	36.0	0.4	34.4	20.6	25.6	13.0	23.8	23.4	0.0	30.6	61.2
Unbalanced (75/25 split)	4,500	1,500	61.8	1.0	22.4	53.8	31.1	3.7	3.7	25.0	0.0	12.2	63.0
	2,250	750	52.2	0.0	6.8	29.4	29.3	7.3	7.6	22.0	0.0	24.0	67.4
	750	250	40.6	0.4	6.4	18.2	24.5	10.1	10.9	18.8	0.0	32.4	73.2
	375	125	38.2	0.0	15.0	22.8	28.9	15.0	17.3	22.4	0.0	32.8	65.6
	150	50	37.0	0.4	36.0	21.4	29.4	16.4	26.1	27.2	0.0	32.6	61.0

Note. AIC = Akaike information criterion; aBIC = adjusted bayesian information criterion. % BIC is the percentage of simulations selecting this model using the Bayesian information criteria and BLRT is the bootstrap likelihood ratio test.

Conclusion

Our initial simulations examined the effects of sample size on regression mixture models when the only feature defining latent classes was the heterogeneous effects of a predictor on an outcome. We deliberately chose a simulation scenario that was ideal in terms of distributional assumptions and the number of latent classes but rendered more difficult by the very weak class separation caused by the lack of mean differences between classes in the outcome and no other predictors with which to separate the latent classes. We showed that, in such circumstances, entropy in the true model is very low and that model convergence to a replicated LL value becomes increasingly unlikely as sample sizes drop to 1,000 or less. None of the model-selection criteria were effective in selecting the true model when samples were less than 3,000 although when a preponderance of evidence was used, the correct solution could be found with samples of 1,000. The problem appears to be not only a lack of power but also the selection of solutions with superfluous, typically very small, classes. The problem is reduced if solutions with small classes are eliminated from consideration, this leaves open the question of how to find true small classes. We suspect that in this case either substantial class separation or very large sample sizes will be needed. We found that, with the ordinal logistic regression model and no intercept differences it was possible to arrive at the right number of classes only if a preponderance of the evidence was used—an approach that implies never choosing solutions with any classes that contain 10% or less of the respondents. We note that a limitation of this study is that we only examined a true model with two classes. We hypothesize, but did not test, that adding additional classes without increasing class separation would increase required sample size because of the need to estimate more parameters without having much additional information.

When the correct number of latent classes were found, model parameter estimates were on average reasonable, except for class sizes of 500 and below. However, this hides an additional issue. With sample sizes this small, there were many cases in which multiple classes were supported and apparently reasonable solutions found, but where the parameter estimates were extreme, or even opposite of the true values. Although regression mixture models work well with large samples, using such models with small samples appears to be a dangerous proposition.

To better understand these results we further investigated the effects of class separation on required sample size, showing that increasing class separation led to adequate results with samples of 500 and decreasing class separation resulted in samples of 1,000 being inadequate to find differential effects (the correct number of classes). A promising result came from including additional predictors in the model, in this case model performance improved dramatically.

Applied Example

Introduction

To illustrate the issues that can arise in practice when small samples are used in regression mixture models, we analyzed data from a previously published study that used regression mixtures to examine heterogeneity in the effects of family resources on academic achievement (Van Horn et al., 2009). Specifically, that prior study identified three latent classes: one defined by low achievement (especially in reading but also in mathematics outcomes), one defined by a strong effect of basic needs (e.g., housing, food, and clothing), and the last being resilient to the effects of a lack of basic needs. Because the latter two classes had similar means for achievement, the class separation between them was weak. Nevertheless, the three classes appeared to be robust, especially with regard to the inclusion of covariates, and the study had a sample size of 6,305. These data provide us with an opportunity for assessing what would have happened if a smaller data set had been used with applied rather than simulated data.

Method

Data were collected between 1992 and 1997 as part of the National Head Start Transition study: a 30-site longitudinal intervention study (for a full description, see C. T. Ramey, Ramey, & Phillips, 1996; S. L. Ramey et al., 2001). The sample consisted of children who had formerly been in the Head Start program and their peers from the same classrooms. Family resources were assessed using the Family Resource Scale (Dunst & Leet, 1994; Dunst, Leet, & Trivette, 1988), an instrument designed to measure the resources and needs of families of high-risk children. The Family Resource Scale assesses four aspects: ability to meet basic needs, adequacy of financial resources, amount of time spent together, and amount of time parents have for themselves (Van Horn, Bellis, & Snyder, 2001). Children’s receptive language skills were measured with the Peabody Picture Vocabulary Test–Revised (Dunn & Dunn, 1981), a predictor of school performance among low-income children (McLoyd, 1998). To demonstrate the method, our analyses were run using third-grade data only, collected in 1996 and 1997.

Analyses were run on the full data set that includes 6,305 students. To assess the effects of running regression mixtures on small samples we drew 500 replications without replacement from the full data set of the same four sizes used in the simulation study described above (i.e., n = 200, 500, 1,000, and 3,000). For each sample-size condition, analyses were run for all 500 data sets to evaluate the effect of sample size on class enumeration and parameter estimates, using the same methods as in our simulations. Given that the true population values for the empirical data were not known, we assessed the differences in the model results between the full data set with 6,305 cases and the subsets of the data with smaller sample sizes. We were especially interested in the between-subsample differences within each condition, as these would indicate the range of results that might arise across many small samples. To reduce model complexity, we conducted a regression mixture model with only receptive language as the outcome; this differs from the previously published results, which included reading, math, and language as measures of student achievement (Van Horn et al., 2009). Because the previously identified low-achieving class had lower outcomes for reading and mathematics than the other two classes, but about the same outcome for language, we hypothesized that having language as the only outcome would result in two rather than three classes being identified.

Results

The first step in this phase of our analyses was to examine the regression mixture solution for the full sample. The BIC chose a two-class solution in the full sample, the aBIC was more equivocal: with the two- and three-class solutions being about the same, but the latter’s third class was small, with 8% of the students. We chose to retain the two-class solution. The classes were similar in substance to those already published; the first class containing 27% of the students, and defined by a strong positive effect of basic needs (B = 3.93, SE = 0.71) and a weaker negative effect of time spent with family (B = −1.76, SE = 0.71), and the second class with 73% of the students, featuring a weak positive effect of money (B = 0.83, SE = 0.31) and a weak negative effect of time spent with family (B = −0.56, SE = 0.27). The intercepts for the two classes were quite similar, B = 98.74, SE = 0.67 in class one and B = 101.07, SE = 0.27 in Class 2.

Turning to our multiple replications of each smaller subsample, the first interesting result concerns model convergence. In simulated data, there were convergence problems for the two-class model in about 30% of the simulations with sample sizes of 200, and convergence was a problem in most simulations for the three-class model. With the applied data, however, convergence was rarely a problem with a sample of 200, the two-class model converged 96% of the time, and the three-class model converged 94% of the time. This is consistent with previous results in which convergence became a problem when models were overparameterized with simulated data that were perfectly behaved (Van Horn et al., 2015), but convergence is generally not a problem with applied data, which never perfectly meets model assumptions. While convergence was not a problem with the applied data, replicating the two-class solution was much more difficult. With a sample size of 3,000, only 141 of the 500 replications chose the two-class over the one-class and three-class models using the BIC. This fell to 73 out of 500 replications when the sample size was reduced to 1,000, but then went back up again to 154 out of 500 replications when the sample fell further, to 500, and edged up again, to 181 out of 500 replications, with the very lowest sample size, 200. By this criterion alone, then, it appeared that a sample size of 200 yielded the best model performance. We further explored these results by taking the size of the smallest class into account. When classes that contained less than 5% of the students were excluded from consideration, the two-class model was chosen 140 times with a sample of 3,000, less than 5 times when the sample was 1,000 or 500, and 139 times when it was 200. Results indicate that class enumeration varies greatly as a function of sample size, and that applied data often show different properties than simulated data.

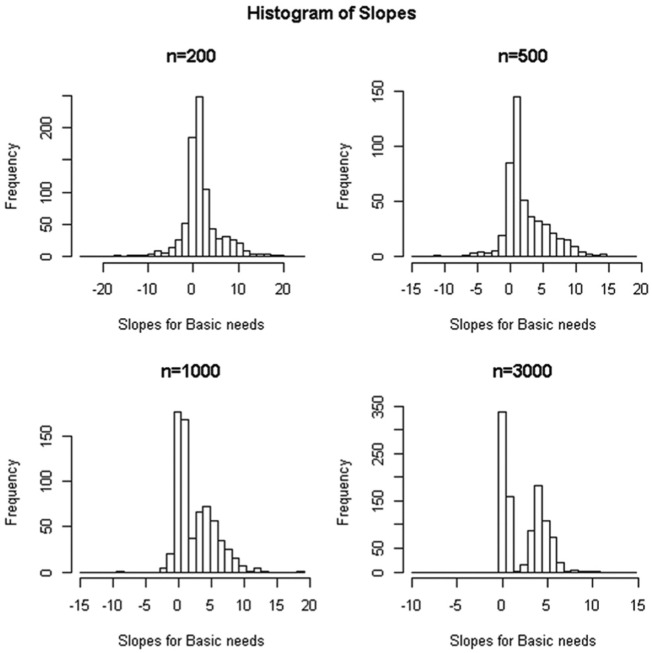
Finally, we examined parameter estimates across replications within each condition. Here, we focused on the regression weight for the effects of students’ basic needs, looking only at those cases where the smallest class contained more than 5% of the sample, since cases with smaller classes than that typically had extreme outliers. In other words, we assumed that the analyst would have arrived at the two-class model even if the model-selection criteria did not clearly indicate support for two classes. The number of 500 simulations for which the smallest class in the two-class solution contained more than 5% of the students was 411 when the sample size was 200, 242 when it was 500, 346 when it was 1,000, and 496 when it was 3,000. Figure 2 presents histograms of regression weights for the effects of basic needs for each condition, and the full model results are included in the appendix. Classes are not sorted here (since it would clearly be problematic in the small-sample conditions), if the solution is stable and matches the full data set—we should see two relatively normal distributions, with one centered on about 0.2 (the nonsignificant effect of basic needs in the resilient class) and the other centered on about 3.9. When the sample size was 3,000, the results mirrored this with nearly complete separation between the different classes. Thus, any two-class solution with a sample of 3,000 would lead to similar results, with only a few outliers. With a sample size of 1,000, the slopes were still stable most of the time, although their distributions in the two classes now clearly overlap. It is interesting to note that in the smaller class (i.e., of students more affected by basic needs), the average standard error for the effect of basic needs was 1.7 across all replications. The observed sampling distribution for the largest class across all replications was 2.1, larger than would be suggested by the estimated standard error. Finally, the model results mostly break down with samples of 500 and 200, which provided vague, general evidence for the existence of the class with no basic-need effects, but rarely replicated the results from the full sample.

Figure 2.

Histogram of the slope for basic needs as a function of sample size.

Conclusions

Examining small sample sizes by resampling a previously published example data set confirmed a previous antidotal finding that convergence issues were more common when working with simulated rather than applied data. The reason for this may be that simulated data meet all model assumptions, whereas applied data typically violate assumptions to some degree. These results also showed that in applied situations there may be more variability in the number of classes chosen than in simulated data: even with sample sizes of 3,000 and when the model results appear stable across samples, model-selection criteria chose two classes only about half the time. Finally, while parameter estimates were reasonable and exhibited little variability when the sample size was 3,000, they were markedly more variable with a sample of 1,000, and became quite poor when the samples were 500 or smaller. In many cases, the practical result of this would be a failure to find differential effects due to a one-class model being selected. In other cases, however, using small samples would not only yield quite inaccurate results but also estimated standard errors that give the researcher a false sense of confidence in such results.

General Discussion

One of the most common questions asked at presentations on regression mixture models concerns the sample size required to use this method. Our purpose in this study was to help applied researchers understand the interplay between class separation and sample size when estimating regression mixture models with continuous and ordinal outcomes. Looking across all results of this study suggests that (a) when class separation is low (as is typical in regression mixtures), sample sizes as much as an order of magnitude greater than suggested by previous research may be needed to obtain stable results; (b) there is a direct relationship between class separation and required sample size such that increasing class separation would make most results stable, although potentially at the cost of losing what made a regression mixture useful; (c) regression mixtures with ordinal outcomes result in even more instability; (d) with small samples it is possible to obtain spurious results without any clear indication of there being a problem; (e) very small latent classes may be an indicator of a spurious result (it is not clear to us how truly small classes can be reliably identified when class separation is low); (f) higher values of entropy are not necessarily indicative of a correct model; and (g) at least within the range of a 25% to 75% split between classes, the effects of class size were less in our study than of sample size.

This article’s most striking finding is that—when sample sizes were small (e.g., less than 1,000 in the conditions studied)—some simulations or replications arrived at results that not only differed dramatically from the true effects in the population but also were undetectable as incorrect. Users of regression mixture models need to realize that, especially when sample sizes are small, it is readily possible to build a model that converges to a solution that is apparently reasonable, but in reality is merely an artifact of the data set. As well as emphasizing the need for samples of an adequate size, this implies that both increasing class separation and using additional methods for protecting against spurious results are needed. As noted in these results, class separation can be improved by increasing the number of predictors or outcomes. Increased class separation can also be achieved by including covariates that affect class membership, although previous work has noted that this may also lead to its own set of problems (Kim, Vermunt, Bakk, Jaki, & Van Horn, 2016). We therefore stress the importance of testing theories that have been developed a priori, and of ultimately including predictors of latent classes in the model to test for expected effects. Other ways to guard against spurious findings may include testing alternative model parameterizations, such as by using (a) ordered logistic regression models (Van Horn et al., 2012) (although it should be noted that class enumeration with these models appears to require even larger samples than are required for continuous outcomes); (b) differential effects sets (George, Yang, Jaki, et al., 2013); or (c) skewed normal distributions (Liu & Lin, 2014). Finally, validating results with independent samples and with other outcomes that should serve as proxies for the primary outcome may help guard against spurious results.

However, many more questions remain to be answered, including (a) Do sample-size requirements go up proportionally as the number of true classes increases? (b) Are even larger samples required if there are larger differences than 75/25 in the population split between classes? (c) How are a model’s sample-size requirements affected by its inclusion of more than one predictor or more than one outcome? (d) How does violation of distributional assumptions affect sample-size requirements? Future investigation might also usefully include increases in the number of observations per person. An additional limitation of this study is that conditions with unequal proportions between the two classes were generated in such a way that the stronger regression weight was always given to the class containing the greater number of individuals; and though we would expect similar results for the opposite case, it was not tested. Nevertheless, while many more different scenarios could be tested, this study does serve to illustrate the types of problems that may occur when using regression mixtures with even moderately small samples.

Appendix

Full Results From Applied Regression Mixture Models

Full results for the analyses of the applied data set with different sample sizes are presented in this appendix. Table A1 presents the class enumeration results using the Bayesian information criterion (BIC) and adjusted BIC (aBIC) for the full data set.

Table A1.

Class Enumeration for the Full Data Set (n = 6,305).

BIC				aBIC
One-class	Two-class	Three-class	Four-class	One-class	Two-class	Three-class	Four-class
42522.8	42478.5	42496.0	42505.2	42494.2	42427.7	42422.9	42409.9

Note. BIC = Bayesian information criterion; aBIC = adjusted bayesian information criterion.

We next examine latent class enumeration for the smaller subsamples of the applied data, meant to simulate what would happen across many smaller subsamples of the data. Results in Table A2 indicate that even when the subsample size is 3,000, neither the BIC nor the aBIC do a great job of selecting the same two-class solution found in the full data set.

Table A2.

Number of Simulations Where the Smallest Class Was Above 5% of the Sample Selecting the Two-, Three-, and Four-Class Solutions With BIC and aBIC.

		BIC				aBIC
	N > 5%a	Two-class over one-class	Three-class over one-class/two-class	Four-class over one-class/two-class/three-class	Two-class over one-class/three-class	Two-class over one-class	Three-class over one-class/two-class	Four-class over one-class/two-class/three-class	Two-class over one-class/three-class
n200	411	222	83	16	139	347	294	241	53
n500	242	6	3	2	3	123	105	89	18
n1000	346	10	5	1	5	152	99	74	53
n3000	496	157	17	0	140	360	82	46	278

Note. BIC = Bayesian information criterion; aBIC = adjusted bayesian information criterion.

^aNumber of simulations containing at least 5% of subjects in the smallest class.

Finally, we examine the parameter estimates for the full data set and each of the smaller subsamples. Results in Table A3 indicate that the mean estimates tend to be quite close to those observed in the full sample, but that there is extensive variability across estimates. This can especially be seen in the difference between the average standard errors and the standard deviation across subsamples in each of the parameters. There is substantially more variability observed than the standard errors suggest should be there. Estimates of the standard errors appear to underestimate the sampling variability at low samples.

Table A3.

Parameter Estimates for Subsets of Applied Data.

	N = 200
	Basic needs			Resilient
	Est.	SE	SD	Est.	SE	SD
Intercept	98.19	0.64	6.13	101.99	0.53	4.79
Basic needs	4.15	0.82	3.81	−0.66	0.58	2.64
Money	0.93	0.85	4.38	0.69	0.67	3.31
Time-self	−1.31	0.85	4.29	0.17	0.66	2.96
Time-family	−2.24	0.88	4.48	−0.34	0.69	3.47
African American	−2.45	0.38	1.34	−2.45	0.38	1.34
Hispanic	−1.25	0.58	2.26	−1.25	0.58	2.26
White	4.81	0.37	1.34	4.81	0.37	1.34
Residual	22.35	4.19	21.71	24.33	3.84	20.16
Class proportion	44.18%			55.82%
	N = 500
	Basic needs			Resilient
	Est.	SE	SD	Est.	SE	SD
Intercept	97.33	1.63	4.20	101.35	0.89	2.05
Basic needs	4.60	1.79	2.85	0.07	0.70	1.46
Money	1.83	1.84	3.29	0.65	0.96	1.57
Time-self	−1.51	1.86	3.06	0.23	0.93	1.75
Time-family	−2.24	1.71	3.07	−0.64	0.89	1.52
African American	−2.51	0.62	0.70	−2.51	0.62	0.70
Hispanic	−1.41	1.01	1.09	−1.41	1.01	1.09
White	4.73	0.59	0.60	4.73	0.59	0.60
Residual	37.06	12.87	27.60	35.28	6.48	17.75
Class proportion	31.99%			68.01%
	N = 1,000
	Basic needs			Resilient
	Est.	SE	SD	Est.	SE	SD
Intercept	97.37	1.43	2.79	101.35	0.67	0.99
Basic needs	4.71	1.65	2.43	0.19	0.56	0.77
Money	1.98	1.57	2.26	0.58	0.75	1.12
Time-self	−1.43	1.55	2.08	−0.05	0.68	0.86
Time-family	−2.63	1.68	2.68	−0.37	0.67	1.04
African American	−2.52	0.44	0.42	−2.52	0.44	0.42
Hispanic	−1.38	0.72	0.65	−1.38	0.72	0.65
White	4.65	0.42	0.39	4.65	0.42	0.39
Residual	51.50	13.58	25.77	36.89	5.65	12.34
Class proportion	28.50%			71.50%
	N = 3000
	Basic needs			Resilient
	Est.	SE	SD	Est.	SE	SD
Intercept	97.77	1.08	1.68	101.14	0.37	0.33
Basic needs	4.37	1.18	1.05	0.30	0.27	0.23
Money	1.82	1.14	1.22	0.76	0.38	0.33
Time-self	−1.51	1.12	0.98	−0.05	0.34	0.26
Time-family	−2.07	1.16	0.91	−0.57	0.37	0.27
African American	−2.52	0.25	0.17	−2.52	0.25	0.17
Hispanic	−1.39	0.41	0.30	−1.39	0.41	0.30
White	4.68	0.24	0.18	4.68	0.24	0.18
Residual	67.48	12.33	17.86	37.19	2.94	3.40
Class proportion	23.42%			76.58%
		N = 6,305
		Basic needs		Resilient
		Est.	SE	Est.	SE
Intercept		98.76	0.67	101.07	0.27
Basic needs		3.93	0.71	0.20	0.17
Money		1.31	0.86	0.83	0.31
Time-self		−1.22	0.68	−0.07	0.24
Time-family		−1.76	0.71	−0.56	0.27
African American		−2.52	0.17	−2.52	0.17
Hispanic		−1.37	0.28	−1.37	0.28
White		4.67	0.16	4.67	0.16
Residual		77.02	8.19	35.58	1.97
Class proportion		26.63%		73.37%

Note. Est. = estimate; SE = standard error; SD = standard deviation.