Voltage-Dependent Membrane Properties Shape the Size But Not the Frequency Content of Spontaneous Voltage Fluctuations in Layer 2/3 Somatosensory Cortex

Abstract

Under awake and idling conditions, spontaneous intracellular membrane voltage is characterized by large, synchronous, low-frequency fluctuations. Although these properties reflect correlations in synaptic inputs, intrinsic membrane properties often indicate voltage-dependent changes in membrane resistance and time constant values that can amplify and help to generate low-frequency voltage fluctuations. The specific contribution of intrinsic and synaptic factors to the generation of spontaneous fluctuations, however, remains poorly understood. Using visually guided intracellular recordings of somatosensory layer 2/3 pyramidal cells and interneurons in awake male and female mice, we measured the spectrum and size of voltage fluctuation and intrinsic cellular properties at different voltages. In both cell types, depolarizing neurons increased the size of voltage fluctuations. Amplitude changes scaled with voltage-dependent changes in membrane input resistance. Because of the small membrane time constants observed in both pyramidal cells and interneuron cell bodies, the low-frequency content of membrane fluctuations reflects correlations in the synaptic current inputs rather than significant filtering associated with membrane capacitance. Further, blocking synaptic inputs minimally altered somatic membrane resistance and time constant values. Overall, these results indicate that spontaneous synaptic inputs generate a low-conductance state in which the amplitude, but not frequency structure, is influenced by intrinsic membrane properties.

SIGNIFICANCE STATEMENT In the absence of sensory drive, cortical activity in awake animals is associated with self-generated and seemingly random membrane voltage fluctuations characterized by large amplitude and low frequency. Partially, these properties reflect correlations in synaptic input. Nonetheless, neurons express voltage-dependent intrinsic properties that can potentially influence the amplitude and frequency of spontaneous activity. Using visually guided intracellular recordings of cortical neurons in awake mice, we measured the voltage dependence of spontaneous voltage fluctuations and intrinsic membrane properties. We show that voltage-dependent changes in membrane resistance amplify synaptic activity, whereas the frequency of voltage fluctuations reflects correlations in synaptic inputs. Last, synaptic activity has a small impact on intrinsic membrane properties in both pyramidal cells and interneurons.

Introduction

Cortical processing results from the interaction between spontaneous intracellular voltage activity and sensory drive (Arieli et al., 1996; Kenet et al., 2003; Petersen et al., 2003; Destexhe, 2011; Reimer et al., 2014; McGinley et al., 2015a,b). Although many studies have carefully quantified the voltage and current activity in response to sensory inputs (Borg-Graham et al., 1998; Priebe and Ferster, 2005; Crochet and Petersen, 2006), much less is known about spontaneous events. In the absence of sensory input, intracellular cortical activity in awake animals is associated with large, self-generated, low-frequency membrane voltage fluctuations (Crochet and Petersen, 2006; Bennett et al., 2013; Reimer et al., 2014; Tan et al., 2014; McGinley et al., 2015b; Perrenoud et al., 2016). Although correlations in synaptic inputs undoubtedly help to shape intracellular spontaneous activity, the role of intrinsic membrane properties remains unclear.

In somatosensory cortex, intracellular recordings in layer 2/3 pyramidal cells from anesthetized rats have shown that membrane input resistance increases with depolarization (Waters and Helmchen, 2006). In awake mice, these types of intrinsic properties have been shown to determine the size and duration of synaptic-mediated membrane depolarizations in hypothalamic neurons (Branco et al., 2016). Similar biophysical mechanisms have been established to affect intracellular depolarizations during place cell activity in hippocampal pyramidal cells (Lee et al., 2012; Hsu et al., 2018). Further, in active slices that generate up–down state transitions (Shu et al., 2003), voltage-dependent currents have been shown to influence intracellular membrane voltage changes (Sanchez-Vives and McCormick, 2000; Compte et al., 2003). Therefore, in addition to being shaped by correlations in synaptic inputs, the size and frequency structure of spontaneous voltage fluctuations can be influenced by voltage-dependent changes in membrane input resistance and integration time. Cortical circuits under awake and anesthetized conditions, however, are often associated with a high-conductance state brought on by synaptic activity that reduces intrinsic membrane input resistance and time constant values (Paré et al., 1998; Destexhe and Paré, 1999; Destexhe et al., 2003), as well as any potential voltage dependence in these two properties (Fernandez et al., 2018). Given this possibility, it remains unknown how or if intrinsic membrane properties help to shape intracellular spontaneous cortical activity.

To help elucidate the mechanisms underlying spontaneous membrane voltage fluctuations, we performed intracellular recordings in primary somatosensory cortex in awake, head-fixed mice. Membrane voltage and current fluctuations were characterized at different voltages in layer 2/3 pyramidal cells and interneurons. Both populations of neurons expressed voltage fluctuations dominated by low-frequency power and with amplitudes that increased with membrane depolarization at the cell body. Synaptic currents in voltage clamp shared similar spectral properties to those of membrane voltage fluctuations. Synaptic current amplitude, however, did not change significantly with depolarization. Instead, the increase in voltage fluctuation amplitude resulted from voltage-dependent changes in membrane input resistance that were present in both pyramidal cells and interneurons. Although the membrane time constant of cortical neurons also increased with depolarization, values were always much smaller than the duration of synaptic current fluctuations. Finally, in both cell types, local application of TTX, which silenced synaptic-mediated membrane voltage fluctuations, minimally affected steady-state resistance and time constant values. The frequency structure of membrane voltage fluctuations, therefore, largely reflects correlations in synaptic inputs, whereas the amplitude is heavily influenced by intrinsic changes in membrane input resistance.

Materials and Methods

Ethics statement.

All experimental protocols were approved by the Boston University Institutional Animal Care and Use Committee.

Surgeries.

Before surgery, mice (2–10 months old of either sex) were anesthetized using ketamine (80–100 mg/kg) and xylazine (8–10 mg/kg). The local anesthetic bupivacaine (1%) was injected subcutaneously near the site of the surgical incision. The animal received an injection of the buprenorphine (0.2–0.5 mg/kg) before surgery. Throughout the surgery, the animal's body temperature was maintained at 37°C using a water-based heating pad and vitals [heart rate 125–250 beats/min and estimated oxygen saturation (SPO₂): 75–99% during surgeries] monitored using a pulse oximeter (Kent Scientific). Ointment was applied to the eyes during surgery to prevent drying. Access to cortical neurons was accomplished using an ∼4 mm² cranial window over cortical area S1 that permitted wide-field visualization and insertion of a standard patch-clamp electrode. A cranial window was centered at 2.5 mm rostral from lambda and 4.5–5 mm lateral from the midline. The cranial window was created with a dental drill and formed within the confines of an aluminum head frame that was anchored to the skull using dental cement and cyanoacrylate. To facilitate electrode access and imaging, the meninges were removed using a small curved needle. To minimize movements associated with mechanical perturbations and to prevent exposure of brain tissue, the cranial window was filled with 2% (weight/volume) low-melting point agarose, which was dissolved in a sodium chloride solution (0.9% weight/volume). The window was then partially covered using a square glass coverslip. After surgery, the mouse was allowed to recover for a period of at least 2 h so that it was fully awake (heart rate >350 beats/min) and moving. During recordings, the mouse's head was fixed to a custom aluminum frame and the mouse was partially restrained using either a semi-enclosed tube or flexible 3M Health Care Coban Wrap. A brief 30 min habituation period was provided before the recording session. For all recordings, the mouse was placed in a chamber that minimized light and sound and provided a quiet environment. During placement in the recording chamber, the animal was kept warmed using a water-based heating pad. For some experiments, vitals were monitored (heart rates were always >400 beats/min and SPO₂ > 95%).

Visualizing cortical layer 2/3 neurons and the pipette electrode.

To visualize layer 2/3 excitatory pyramidal cells and inhibitory interneurons in somatosensory cortex, we used the CaMK2a and GAD2 promoters, which are expressed in excitatory pyramidal cells and inhibitory interneurons, respectively. For excitatory neurons, C57BL/6J background, CaMK2a-Cre mice (Tsien et al., 1996) (The Jackson Laboratory, stock #005359) were crossed with the lox-stop-lox tdTomato reporter mice (Zariwala et al., 2011) (The Jackson Laboratory, stock #007914). The same reporter mouse was crossed to GAD2-Cre mice (Taniguchi et al., 2011) (The Jackson Laboratory, stock #010802) to visualize inhibitory interneurons.

The electrode pipette was visualized using the cyan-green fluorescent dye Alexa Fluor 488 hydrazide (Thermo Fisher Scientific), which was added to the intracellular electrode solution (0.3% weight/volume). Imaging was performed using a two-photon imaging system (Thorlabs) with a mode-locked Ti:Sapphire laser (Chameleon Ultra II; Coherent Technologies) set to wavelengths between 920 and 950 nm, which was used to excite both the Alexa Fluor 488 and tdTomato using a 20×, 1.0 numerical aperture (Olympus) objective lens. Laser scanning was performed using resonant scanners and fluorescence was detected using two photo-multiplier tubes (Hamamatsu) equipped with red and green filters to separate emission from Alexa Fluor 488 and tdTomato.

Electrophysiology.

The space between the pial surface and the objective lens was filled with artificial CSF consisting of the following (in mm): NaCl (125), NaHCO₃ (25), d-glucose (25), KCl (2), CaCl₂ (2), NaH₂PO₄ (1.25), and MgCl₂ (1). A ground electrode consisting of a silver chloride wire was placed inside the cranial window. Recordings of intracellular membrane voltage or current were performed using standard patch-clamp electrodes with tips (0.6–1 μm) and resistance values between 7 and 12 MΩ. Electrodes were pulled using a horizontal puller (Sutter Instruments) using filamented, thin-wall glass (Sutter Instruments). Intracellular pipette solution consisted of the following (in mm): K-gluconate (120), KCl (20), HEPES (10), diTrisPhCr (7), Na₂ATP (4), MgCl₂ (2), Tris-GTP (0.3), and EGTA (0.2) buffered to pH 7.3 with KOH.

Electrodes were lowered into layer 2/3 of cortex ∼150–275 μm below the pial surface using a micromanipulator (Sutter Instruments). A variable amount of positive pressure was used to penetrate the agar and pial surface. Under visual guidance, the pressure was then gradually reduced when approaching neurons to minimize perturbing the cell and to facilitate seal formation. During seal formation, a 5–10 mV voltage step was used to measure seal resistance and the capacitance associated with the glass electrode. Upon seal formation (>2 GΩ) in the on-cell (i.e., cell-attached), capacitance compensation was used to eliminate the pipette capacitance. Small amounts of transient negative pressure were used to break the seal and to establish whole-cell recordings.

Series resistance values for layer 2/3 pyramidal cells and interneurons were 48.7 ± 8.84 MΩ (n = 57) and 53.4 ± 9.78 MΩ (n = 37), respectively (before compensation), with a maximum value of 75 MΩ. In current-clamp recordings, full bridge balance compensation was used, whereas 55–70% series resistance compensation was implemented in voltage-clamp recordings. Throughout recordings, seal resistance was monitored every 2–3 min. Recordings were discarded if changes >10 MΩ were observed. In some cases, in voltage clamp (e.g., quantifying changes in resistance during whisking), quality of recordings was determined by monitoring the current elicited by a hyperpolarization steps (10 or 20 mV) delivered at 2 Hz. Any change in series resistance could be detected as a reduction and change in temporal profile of the current elicited by the voltage step. In addition, in current clamp using bridge balance compensation, membrane time course in response to small current steps were accurately fit with exponential functions (r² > 0.95). Finally, during current injection, any moment-by-moment change in access resistance was easily detected due to the generation of large-sized voltage artifacts that were only present when injecting current. In all such cases, recordings were discarded.

An experimentally measured junction potential of 10 mV was subtracted from all voltage traces. Trace signals were amplified and low-pass filtered at 10 kHz before being digitized at 20 kHz. For LFP recordings, a 0.3–0.6 MΩ electrode filled with ACSF was placed in layer 2/3. LFP recordings were recorded at 20 kHz and filtered between 0.1 and 1000 Hz. All electrophysiology was performed using a Multiclamp 700B (Molecular Devices) and a Digidata 1550 (Molecular Devices).

For comparisons of membrane input resistance during whisking and idling (see Fig. 2F), a hyperpolarizing pulse (−10 or −20 mV, 250 ms duration) was delivered at 2 Hz while voltage clamping the cell at −70 mV. Membrane resistance was taken as the difference in steady-state current during the hyperpolarizing and the steady-state current between pulses. For the plot in Figure 2, Fi and Gi, membrane resistance and current values were averaged across five pulses.

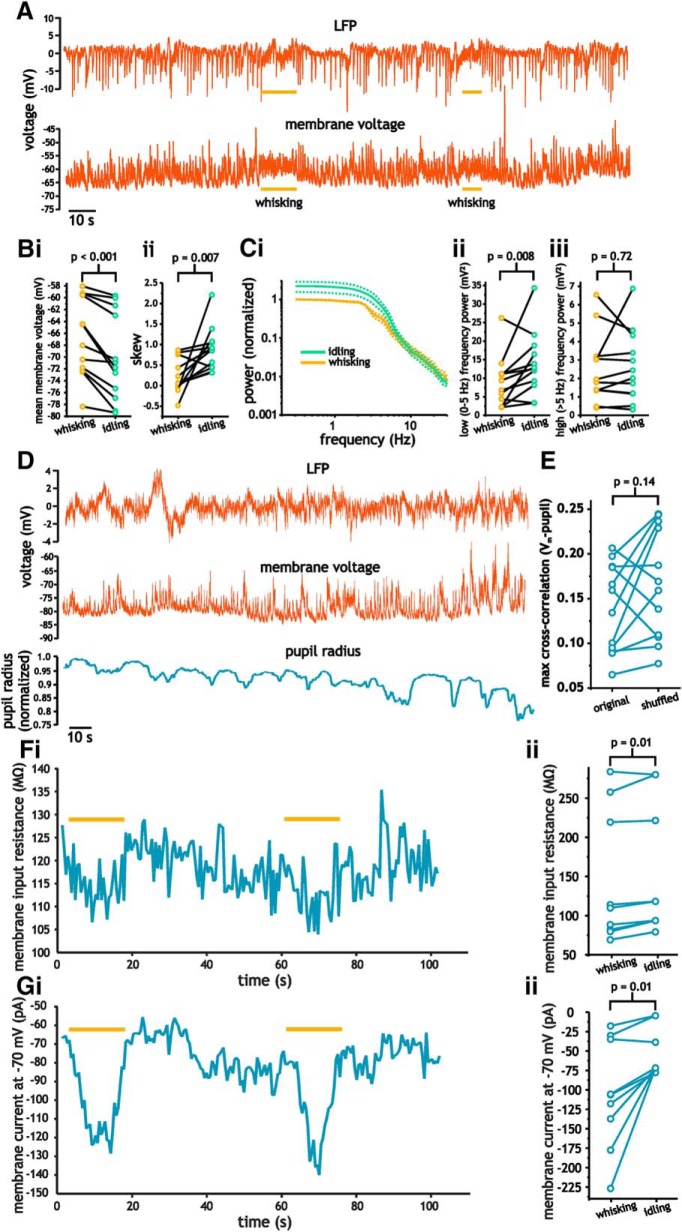
Figure 2.

Correlation of spontaneous membrane voltage fluctuation with whisking and pupil diameter in layer 2/3 pyramidal cells. A, Example intracellular membrane voltage (bottom) and LFP (top) indicating periods of whisking. B, Plots of mean membrane voltage (i) and skewness coefficients (ii) during and before moments of whisking. C, Average power spectra (i) associated with idling and whisking states along with plots of total power below (ii) and above (iii) 5 Hz. Data bars (dashed lines) for spectra indicate SE. D, Simultaneous measures of LFP (top), membrane voltage (middle), and pupil radius (bottom). E, Plot comparing cross-correlation coefficients between pupil radius and membrane voltage using the original and a shuffled trace of membrane voltage. F, G, Plot of membrane resistance (F) and average current (G) during idling and whisking. Plots comparing changes in membrane resistance (Fii) and membrane current (Gii) during idling and whisking.

For TTX application during awake recordings, we used a secondary pipette in close proximity to the recording electrode (100–250 μm away) filled with ACSF and containing 50 μm TTX and Alexa Fluor 488 hydrazide (0.3% weight/volume) to visualize the delivery of TTX during experiments. To ensure the patch electrode stability, we slowly applied pressure through a syringe until the Alexa Fluor 488 was present in the area around the recording electrode and the cessation of membrane voltage fluctuations. Typically, TTX caused synaptic activity to disappear within 1–5 min of application. The variability likely resulted from small changes in the exact location of the injection pipette and distance to the cell being patched. Measures of membrane resistance with TTX were taken once a steady-state reduction in membrane variance was established.

Animal monitoring and pupil measures.

The contralateral (relative to the recording electrodes) side of the animal's face was monitored using a monochromatic camera (FLIR Flea 3; Richmond) coupled to a variable focus lens (f/1.3). Images were captured at 20 frames/s and exported using FLIR software. Illumination was provided either by the two-photon imaging system or and an infrared LED lamp.

Whisking was determined post hoc by visually examining the video recordings and time stamping periods in which whiskers moved. For whisking, we used a threshold in which whiskers (any number of them) could be seen moving for at least 20 frames (1 s). In all cases in which we observed whisking, almost all the whiskers moved together for periods longer than 1 s. Pupil diameter was determined using a supervised algorithm adapted from a previous study (Zoccolan et al., 2010) and based on the Starburst algorithm (Li et al., 2005). The image was first smoothed with a 2D Gaussian filter (σ = 3–5 pixels) to reduce noise. The gradient was then computed by convolving with 2 Sobel kernels in the horizontal and vertical directions. The magnitude of the gradient was then used to indicate the edges in the image. From an initial estimate of the pupil center (acquired manually), equally spaced outgoing rays were used to find points on the pupil boundary. The first point where the change in gradient was greater than a SD along the ray was set as the putative pupil boundary points. A least-squares fit was used to estimate the pupil boundary as a circle from the set of the points on the putative pupil boundary. A second iteration of the algorithm was used to improve the estimate.

Data analyses.

For power spectral density curves and spectrogram analyses, we used the Chronux (http://chronux.org/) analysis software toolkit developed in MATLAB (The MathWorks). For spectrograms, mean-subtracted, 2-min-long current or voltage traces were low-pass filtered at 1000 Hz and then analyzed using a multitaper time–frequency spectrum analysis implemented with the mtspecgramc function included in the Chronux analysis software. The window for the spectrum was set to 10 s. For power spectral density curves, the output from spectrograms was averaged across windows to form a single curve for each data trace. For measures of power, power spectral density curves were integrated between ranges of frequencies specified in the Results section. Autocorrelation analyses and autocorrelograms were generated using the MATLAB function xcorr. The magnitude squared coherence between the LFP and intracellular membrane voltage (see Fig. 1F,G) was calculated with the MATLAB function mscohere with a Hamming window for averaging.

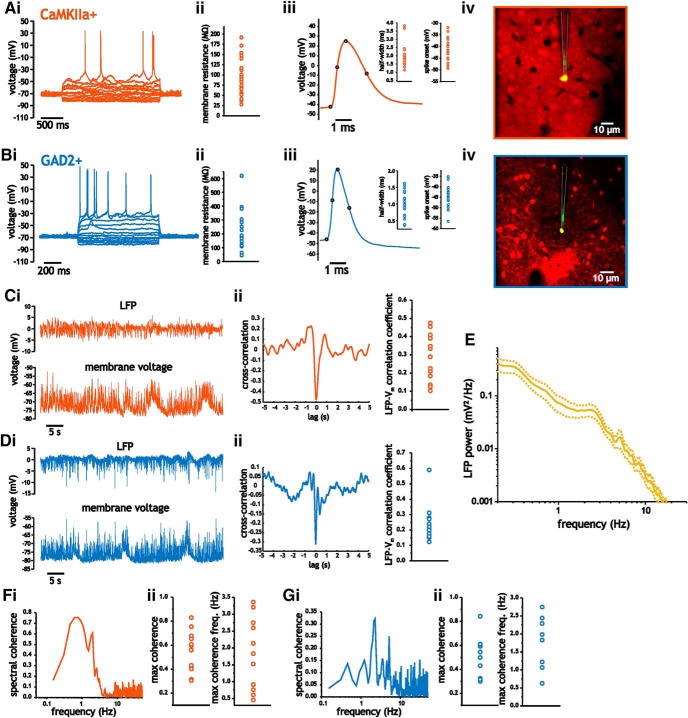
Figure 1.

Characterization of membrane properties, spike shape parameters, and LFP in CaMKIIa- and GAD2-positive neurons from layer 2/3 somatosensory cortex. A, B, Intracellular recordings of CaMKIIa-positive (A) and GAD2-positive (B) layer 2/3 neurons along with mean values of membrane input resistance (ii), spike shape measures (iii), and image (iv) of two-photon-guided intracellular recording. C, D, Simultaneous recording of LFP (i, top) and intracellular membrane voltage (i, bottom) in layer 2/3 somatosensory pyramidal cells (C) and interneurons (D). Representative cross-correlogram (ii) and average peak cross-correlation coefficient (ii, right). E, Average LFP power spectrum. Data bars (dashed lines) for LFP indicate SE. F, G, Quantification of spectral coherence between intracellular membrane voltage and LFP in pyramidal cells (F) and interneurons (G). Representative spectral coherence (i), along with maximum coherence (ii) and frequency, (iii) are shown.

To calculate membrane time constants, we fit the average membrane voltage response (25 trials) to a current step from the onset of the step to a time point 250 ms afterward. Using the same average voltage trace, input resistance values were calculated as the ratio between current step and the voltage response sizes. Exponential fits were performed in MATLAB using the nonlinear least-squares fit. Fits were double-checked in Origin Pro 8.0 (OriginLab) using the exponential fitting function. Data were fit from the onset of the step depolarization to a time point 250 ms afterward. In some cases, due to small amounts of uncompensated bridge balance, fitting was started slightly after the onset of the current stimulus to avoid the series resistance artifact.

Correlations between membrane voltage and pupil radius were quantified using a cross-correlation analysis. For these analyses, the membrane voltage traces were down-sampled to match the 20 Hz pupil radius image recordings. To establish a significance level, we shuffled the membrane voltage trace using 1-s-long segments and compared the original correlation between the unshuffled voltage trace and pupil radius with that of the shuffled trace.

Statistical analyses.

All values, unless stated otherwise, are presented as the mean along with the SD. For power spectral density curves and fraction of power, values were plotted as the mean along with the SE. Normality of data points was established using the Shapiro–Wilk test. Positive results from the Shapiro–Wilk test (p < 0.05) were used to determine the use of parametric or nonparametric statistical tests noted in the Results section. To determine whether voltage fluctuations at rest expressed unimodal distributions, we used the Hartigan test for unimodality implemented in MATLAB (Hartigan and Hartigan, 1985; Pfister et al., 2013). For the Hartigan test, histograms (500 bins) were generated and the cumulative distribution used to test for a departure from a unimodal distribution. As a reference point, dip coefficient values >0.05 along with p-value <0.05 generate visibly discernable bimodal distributions. Skewness coefficients of voltage and current trace histograms were calculated using the following equation:

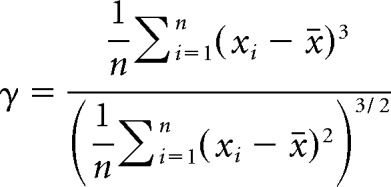Results

Spontaneous membrane voltage fluctuations in layer 2/3 CAMIIa- and GAD2-positive neurons are correlated with the LFP during quiet and awake states

For all recordings, intracellular voltage fluctuations were measured during waking states in the absence of any overt sensory input. Animals were head fixed and partially constrained from moving by containing them in a semienclosed tube or flexible wrap during recordings. Using two-photon imaging, we targeted mouse somatosensory layer 2/3 pyramidal cells and interneurons for whole-cell patch recordings using the selective expression of tdTomato under control of the CaMKIIa and GAD2 promoters, respectively.

The average subpial recording depth for pyramidal cell recordings was 177 ± 24.2 μm (n = 57). At resting voltages (−62.6 ± 5.2 mV), pyramidal cells had average input resistance values of 90.1 ± 41.6 MΩ (n = 27; Fig. 1Aii). Spikes elicited using small amounts of current injection at low discharge frequencies had half-widths and onset voltages of 2.01 ± 0.70 ms and −41.5 ± 4.8 mV (n = 19), respectively (Fig. 1Aiii). For interneurons, recording depth was 179.5 ± 31.2 μm. At resting potentials (−67.6 ± 4.7 mV), interneurons expressed an average input resistance value of 225 ± 148 MΩ (n = 16; Fig. 1Bii), which was significantly greater than that measured in pyramidal cells (two-sample Student's t test, p < 0.001). Average spike half-width and threshold voltage of interneurons was 1.02 ± 0.37 ms and −44.8 ± 4.8 mV (n = 21), respectively, which were also significantly different from those measured in pyramidal cells (two-sample Student's t test, p < 0.001).

We started by characterizing the LFP under our recording conditions and correlating it with the intracellular membrane voltage of pyramidal cells and interneurons (Fig. 1Ci, Di). As in previous recordings performed under idling (quiet) and awake conditions in rodent somatosensory cortex (Crochet and Petersen, 2006; Okun et al., 2010), we observed significant correlations between intracellular membrane voltage and the LFP. In pyramidal cells, peak cross-correlation coefficients varied between 0.10 and 0.48, with an average value of 0.27 ± 0.12 (Student's t test, p < 0.001, n = 15; Fig. 1Cii). Interneuron membrane voltage showed similar cross-correlation values to those measured in pyramidal cells, with an average coefficient of 0.24 ± 0.12 (Student's t test, p < 0.001, n = 13; Fig. 1Dii). Mean pyramidal cell and interneuron cross-correlation values between membrane voltage and the LFP did not differ significantly (two-sample Student's t test, p = 0.93).

To quantify which frequency components in the intracellular membrane voltage correlated with the LFP, we measured the spectral coherence between intracellular voltage and the LFP (Fig. 1F,G). In pyramidal cells, peak coherence was 0.54 ± 0.17 and occurred at 1.87 ± 1.1 Hz (n = 13; Fig. 1Fii). Similarly, in interneurons, peak coherence was 0.48 ± 0.17 and occurred at 1.97 ± 0.68 Hz (Fig. 1Gii). Neither the maximum coherence nor the frequency at which it occurred differed between the two cell types (two-sample Student's t test, p = 0.48 and p = 0.78). The large correlation between intracellular voltage and LFP, therefore, was generated by the slower frequency components associated with network activity.

Changes in spontaneous membrane voltage fluctuations in pyramidal cells correlate with whisking behavior

Spontaneous activity has been shown to contain different states associated with changes in arousal, attention, whisking, or locomotion (Crochet and Petersen, 2006; Reimer et al., 2014; Tan et al., 2014; McGinley et al., 2015b). To better establish the contribution of different behavioral states to the generation of membrane voltage fluctuations, we monitored whisking and pupil diameter and correlated these measures with intracellular membrane voltage traces.

As in prior studies, contralateral whisking was associated with discernable changes in the properties of pyramidal cell membrane voltage fluctuations and the LFP (Fig. 2A) (Crochet and Petersen, 2006). Comparing periods of whisking and periods before whisking of the same duration revealed significant differences in both the spectral and statistical properties of membrane voltage fluctuations associated with whisking. Whisking induced a significant depolarization (−69.5 ± 7.3 mV vs −66.9 ± 6.7 mV, paired Student's t test, n = 13, p < 0.001; Fig. 2Bi) and a decrease in the skewness coefficient of membrane voltage fluctuations (0.85 ± 0.52 vs 0.20 ± 0.40, paired Student's t test, p = 0.007; Fig. 2Bii). Whisking was also associated with a reduction in power of low-frequency (<5 Hz) membrane voltage fluctuations, with total power <5 Hz being reduced from 12.5 ± 7.2 mV² (median ± IQR) to 9.3 ± 6.8 mV² (median ± IQR; Wilcoxon signed-rank test, p = 0.008; Fig. 2Cii). Power >5 Hz, however, was not significantly changed during whisking (2.6 ± 1.8 mV² vs 2.7 ± 1.9 mV², paired Student's t test, p = 0.72; Fig. 2Ciii).

For pupil measures, we performed a cross-correlation analysis between the pupil radius and membrane voltage. The maximum cross-correlation coefficient was then compared with the cross-correlation between the pupil radius and a shuffled version of the same membrane voltage trace. This analysis did not reveal a significant correlation between changes in pupil radii and membrane voltage fluctuations. Cross-correlation coefficient for the original and shuffled traces were 0.14 ± 0.05 and 0.17 ± 0.06, respectively (paired Student's t test, p = 0.14; Fig. 2E).

Given that whisking induced significant changes in membrane voltage statistics, we investigated whether these changes corresponded to significant changes in membrane resistance and current. To measure this, we voltage clamped pyramidal cells at −70 mV and delivered continuous hyperpolarizing steps to measure membrane resistance while monitoring whisking behavior (Fig. 2Fi). As indicated, whisking led to significant, but modest changes in membrane resistance (153 ± 83.3 MΩ vs 144 ± 84.4 MΩ, paired Student's t test, n = 9, p = 0.01; Fig. 2Fii). Conversely, changes in membrane current were much larger (−55.2 ± 30.6 pA vs −106 ± 70.2 pA, paired Student's t test, n = 9, p = 0.01; Fig. 2Gi, Gii).

Although whisking induced significant changes in membrane voltage fluctuation properties and resistance, these periods constituted a small fraction of the total recording duration. Approximately 8.0 ± 2.8% of the recording duration consisted of whisking periods. For this reason, and as will be shown later, average spectra and statistics of membrane voltage fluctuation were dominated by those associated with non-whisking periods.

Intracellular membrane voltage in layer 2/3 neurons is dominated by low-frequency fluctuations that express positively skewed distributions

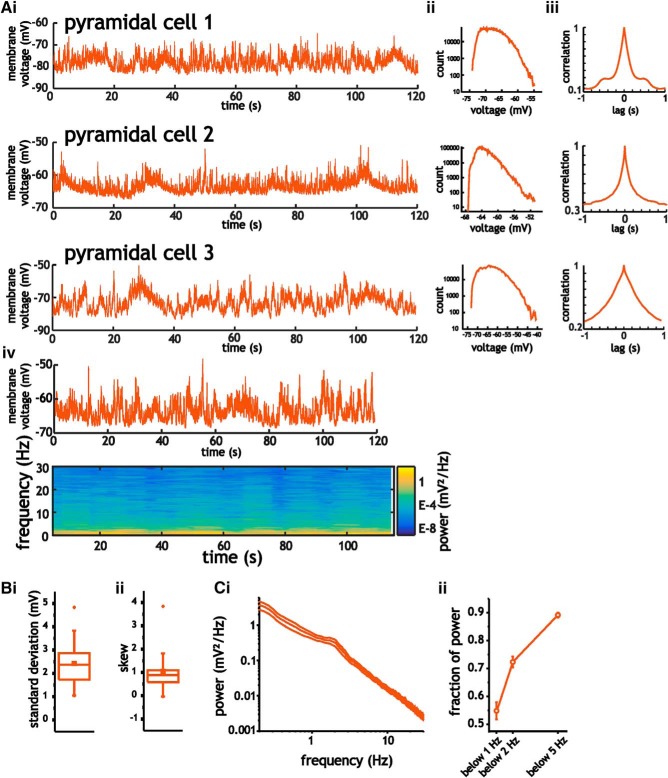
To better establish the statistical and spectral properties of spontaneously generated voltage fluctuations and to accurately measure the power of voltage fluctuations with slow timescales, we used 2-min-long recording periods at resting potentials (Fig. 3A–C). Voltage fluctuations in pyramidal cells had SD values of 2.2 ± 0.89 mV that were characterized by asymmetric histograms with positive skewness coefficients of 1.06 ± 0.805, which were significantly above the zero value expected for a Gaussian distribution (Wilcoxon signed-rank test, p < 0.001, n = 21; Fig. 3B). The distributions of voltage fluctuations, however, were not bimodal. A test for unimodality (the Hartigan dip test; Hartigan and Hartigan, 1985) revealed small average dip coefficients of 0.028 ± 0.02 (mean p-value = 0.36 ± 0.35, n = 21) that are inconsistent with the presence of up–down states. Spectral analyses of voltage fluctuations were dominated by low-frequency power, with 0.89 ± 0.04 (n = 21) fraction of power contained <5 Hz (Fig. 3Cii). Therefore, spontaneous intracellular membrane voltage fluctuations in pyramidal cells were characterized by long correlation times, low-frequency power, and positively skewed distributions.

Figure 3.

Characterization of intracellular membrane voltage fluctuations in layer 2/3 somatosensory pyramidal cells. A, Example traces of 2-min-long intracellular recordings from three different cells (i), along with the corresponding histograms (ii), auto-correlograms (iii), and an example spectrogram (iv). B, Mean SD (i) and skewness coefficient (ii) associated with intracellular membrane voltage traces recorded at rest. C, Mean power spectral density curves for layer 2/3 pyramidal cells calculated using the average power from spectrograms (i), along with average fraction of power at frequencies <5 Hz, 2 Hz, and 1 Hz (ii). For these measures, data bars indicate SE.

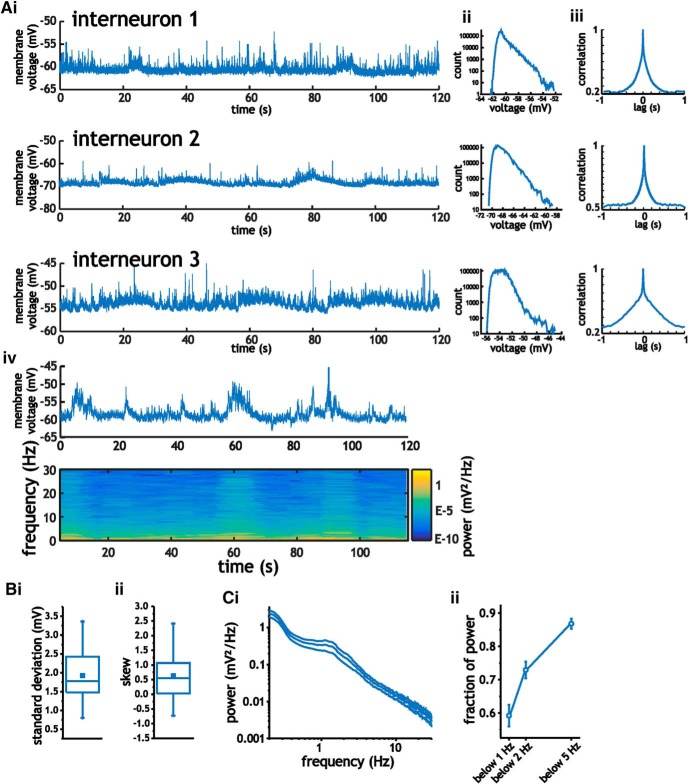
In interneurons, analyses of 2-min-long intracellular recordings at resting voltages showed similar statistical and spectral properties to those observed in pyramidal cells. Interneurons expressed voltage fluctuations with average SD values of 1.9 ± 0.8 mV and a skewness coefficient of 0.63 ± 0.76 (Student's t test, p = 0.002, n = 18), respectively (Fig. 4B). As before, voltage histograms had unimodal distributions with dip coefficients of 0.025 ± 0.01 (mean p-value = 0.18 ± 0.31, n = 18). Power spectral analyses revealed fluctuations with 0.87 ± 0.06 fraction of total power at frequencies <5 Hz (Fig. 4Cii). Like pyramidal cells and consistent with previous recordings from awake rodents in somatosensory cortex (Crochet and Petersen, 2006; Okun et al., 2010), voltage fluctuations in interneurons were dominated by long correlation times, low-frequency power, and positively skewed but unimodal distributions. Although the GAD2-positive population includes different subtypes of interneurons (Ledri et al., 2014), we did not segregate the data because results regarding the spectral profiles were similar across the population. In all 18 cells analyzed, spectral profiles contained >75% of cumulative power <5 Hz. Further, only two of the 18 cells analyzed expressed negative skewness coefficients at resting potentials.

Figure 4.

Characterization of intracellular membrane voltage fluctuations in layer 2/3 somatosensory interneurons. A, Example traces of 2-min-long intracellular recordings from three different cells (i), along with the corresponding histograms (ii), auto-correlograms (iii), and example spectrogram (iv). B, Mean SD (i) and skewness coefficient (ii) associated with intracellular membrane voltage traces recorded at rest. C, Mean power spectral density curves for layer 2/3 interneurons calculated using the average power from spectrograms (i), along with average fraction of power at frequencies <5 Hz, 2 Hz, and 1 Hz (ii). For these measures, data bars indicate SE.

Depolarizing layer 2/3 neurons increases the amplitude of intracellular membrane voltage fluctuations

To explore the factors establishing the properties of spontaneous membrane voltage, we measured the statistical and spectral properties of voltage fluctuations at different voltages using small amounts of current injection. Using whole-cell patch recordings in current-clamp mode with bridge balance compensation, we injected negative and positive current to hold membrane voltage between −95 mV and −45 mV. We limited our maximum depolarization to approximately −45 mV because values more positive than this often led to frequent spiking and the inability to appropriately characterize membrane voltage fluctuations. None of the data used in the analysis of voltage traces included spikes (see Materials and Methods). As before, the statistical and spectral properties of voltage fluctuations in layer 2/3 neurons were quantified using 2-min-long voltage traces at each voltage. Due to differences in resting voltage across different cells, 10 mV binning windows were used for averaging and statistical comparisons.

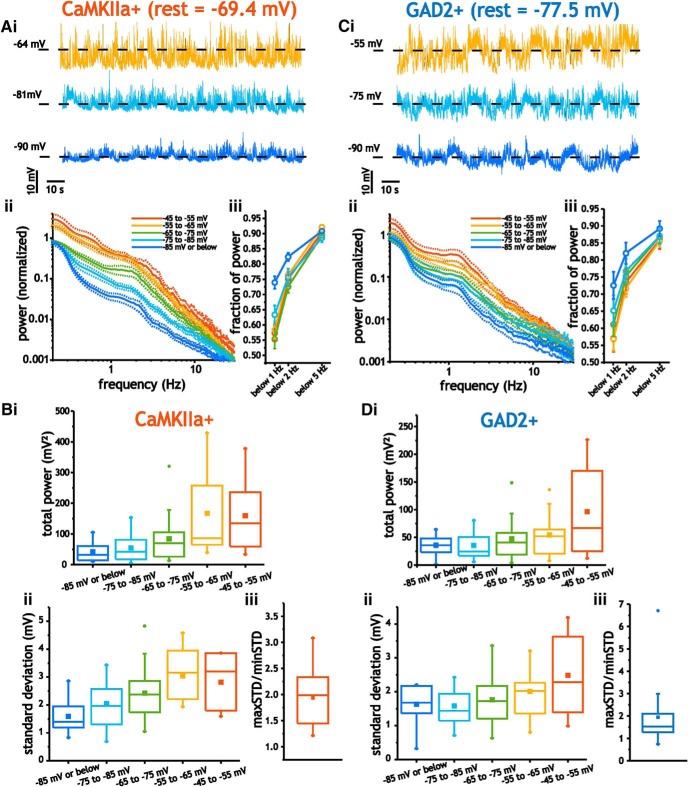
To visualize average power spectral density curves as a function of membrane voltage, we normalized the spectra of individual cells at different voltages to the spectra acquired at the resting potential (no current injected). As cells were depolarized from −95 mV to −45 mV, average spectral density curves for pyramidal cells showed increased power across the entire range of frequencies (Fig. 5Aii). At each voltage, we also quantified the fraction of power in the raw power spectra at frequencies <5 Hz, 2 Hz, and 1 Hz. The power spectra at all holding voltages was always dominated by power at low frequencies. Nevertheless, depolarization from −95 mV to −45 mV led to a slightly lower fraction of power at frequencies <1 and 2 Hz (two-way ANOVA, p = 0.02, n = 7–21; Fig. 5Aiii). Depolarizing pyramidal cells from −95 mV to −45 mv, therefore, led to significant and monotonic increases in the average total power (integrated between 0 and 30 Hz) and SD (one-way ANOVA; p < 0.001, n = 7–21) of membrane voltage fluctuations (Fig. 5Bi, Bii). Going from −95 mV to −45 mV increased total power from 52.3 ± 9.37 mV² to 187.6 ± 50 mV² (Tukey's test, p = 0.04), whereas the SD increased from 1.59 ± 0.57 mV to 3.2 ± 0.36 mV (Tukey's test, p = 0.004). To further confirm that SD increased in individual pyramidal cells, we also measured the ratio between the maximum SD value (usually near ∼−50 mV) and minimum value (usually at ∼−85 mV). This ratio was 1.93 ± 0.54, significantly >1 (Student's t test; p < 0.001, n = 21; Fig. 5Biii), which indicated that the SD of membrane voltage fluctuations increased in individual cells.

Figure 5.

Membrane voltage fluctuations in pyramidal cells and interneurons are voltage dependent. A, Example voltage traces of pyramidal cells at different holding voltages (i), along with the average normalized power spectra (ii) and distribution of power (iii) between −90 and −50 mV. For these measures, data bars represent SE. B, Plots of average power (i), SD (ii), and maxSD/minSD ratio measured between −90 and −50 mV for pyramidal cells. C, Example interneuron voltage traces at different holding voltages (i), along with the average normalized power spectra (ii) and distribution of power (iii) between −90 and −50 mV. D, Plots of average power (i), SD (ii), and maxSD/minSD ratio measured between −90 and −50 mV for interneurons.

For interneurons, power spectral analysis also indicated greater power in fluctuations at depolarized membrane voltages (Fig. 5Ci, Cii). We also noted similar and significant shifts in the distribution of power across 5 Hz, 2 Hz, and 1 Hz with depolarization from −95 mV to −45 mV (two-way ANOVA, p = 0.006, n = 10–16; Fig. 5Ciii). Like pyramidal cells, depolarization led to a significant and monotonic increase in the power and SD of voltage fluctuations (one-way ANOVA; p = 0.01, n = 10–16); power increased from 35.8 ± 19.8 mV² to 96.5 ± 81.3 mV² (Tukey's test, p = 0.004), whereas the SD increased from 1.58 ± 0.56 mV to 2.49 ± 1.19 mV (Tukey's test, p = 0.04; Fig. 5Di, Dii). Further, the ratio of maximum to minimum SD was 1.9 ± 1.4, which, as in pyramidal cells, was significantly >1 (Student's t test; p = 0.006, n = 16; Fig. 5Diii).

Current fluctuation magnitude in layer 2/3 pyramidal cells and interneurons is voltage independent

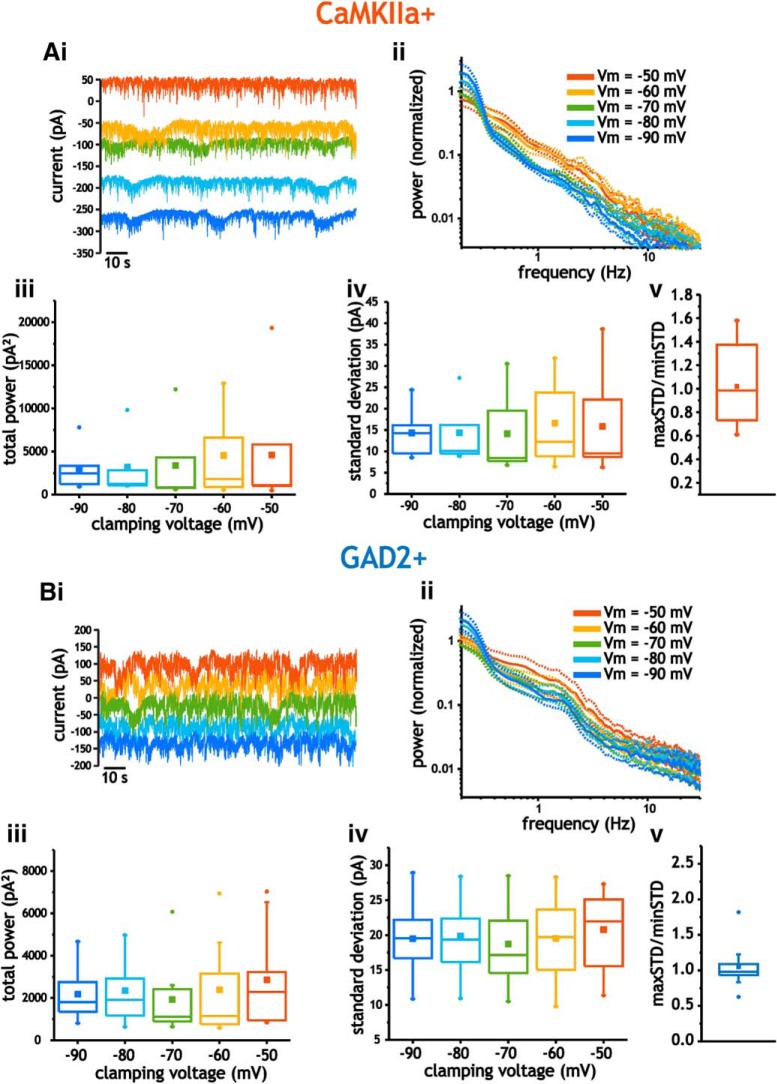
Next, we investigated whether the underlying synaptic currents generating voltage fluctuations increased with depolarization. Alternatively, the increase in size can result from amplification through an increase in intrinsic membrane input resistance with depolarization. To distinguish between the contributions of these two possibilities, we performed intracellular voltage clamp recordings and measured synaptic currents at voltages between −90 mV and −50 mV. At each clamping voltage, power spectra and SD of current fluctuations were measured from 2-min-long recordings.

In pyramidal cells, the average size of current fluctuations did not change across the range of clamping voltages used. Neither the total power (mean value across all voltages = 3689 ± 4470 pA²) nor the SD (mean value = 15 ± 8.5 pA) of current fluctuations was significantly altered by clamping at different voltages (one-way ANOVAs, p > 0.9, n = 5–7; Fig. 6Ai–Aiv). As with membrane voltage fluctuations, we also calculated the ratio between the SD measured at the most depolarized and hyperpolarized voltages. This value was 1.02 ± 0.35, and, unlike the ratio associated with depolarizing membrane voltage, was not significantly different from 1 (Student's t test; p = 0.44, n = 7; Fig. 6Av).

Figure 6.

Analysis of layer 2/3 neuron current fluctuations using voltage clamp. A, Example current traces acquired in pyramidal cells recorded at mean voltages between −90 and −50 mV (i), along with average power spectra (ii), total power (iii), SD (iv), and maxSD/minSD ratio (v). B, Example current traces acquired in interneurons recorded at mean voltages between −90 and −50 mV (i), along with average power spectra (ii), total power (iii), SD (iv), and maxSD/minSD ratio (v). For power spectra, data bars (dashed lines) indicate SE.

Like pyramidal cells, analyses of current fluctuations in interneurons using power spectral density curves indicated that total power did not vary as a function of holding voltage (mean value across all values = 2327 ± 1751 pA²; one-way ANOVA, p = 0.85, n = 10; Fig. 6Bi–Biii). Consistent with this, the SD of current fluctuations was similar across the entire range of voltages tested (mean value = 19.7 ± 5.42 pA₂; one-ANOVA, p = 0.95, n = 10; Fig. 6Biv). Finally, the ratio between the maximum and minimum SD calculated in individual interneuron was 1.05 ± 0.31, which was not significantly different from 1 (Student's t test; p = 0.32, n = 10; Fig. 6Bv). Therefore, in both cell types, the increase in the size of membrane voltage fluctuations with depolarization was not related to a significant increase in the size of synaptic current fluctuations between −90 and −50 mV.

Membrane resistance and time constant values increase with depolarization in pyramidal cells and interneurons

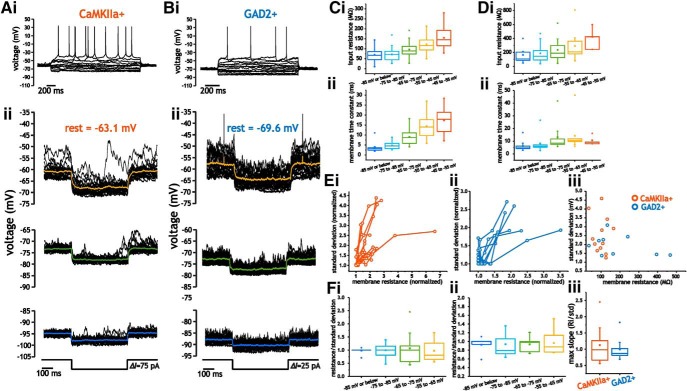
We next investigated whether voltage-dependent changes in intrinsic membrane properties could account for the increase in voltage fluctuations. In some neurons, membrane input resistances and time constants increase with depolarization (Schwindt and Crill, 1977; Waters and Helmchen, 2006; Fernandez et al., 2007, 2015; Naud et al., 2008). To determine whether layer 2/3 neurons expressed changes in intrinsic membrane properties with depolarization, we measured input resistance and time constant using small step depolarizations (5–10 mV) at different holding voltages in pyramidal cells and interneurons (Fig. 7Aii, Bii).

Figure 7.

Pyramidal cells and interneurons express voltage-dependent membrane input resistance and time constant values that scale membrane voltage fluctuations. A, B, Example traces of pyramidal cell (A) and interneuron (B) membrane voltage in response to step hyperpolarizations at different membrane voltages (ii). C, D, Average membrane input resistance (i) and time constant (ii) values measured between −90 and −50 mV for pyramidal cells (C) and interneurons (D). E, Plot of normalized membrane SD as a function of normalized input resistance for pyramidal cells (i) and interneurons (ii). iii, Plot of absolute membrane resistance near rest and the corresponding SD of membrane voltage at the same voltage for pyramidal cells and interneurons. F, Average ratio between normalized resistance and SD measured at different membrane voltages for pyramidal cells (i) and interneurons (ii), along with the maximum value for the ratio in each cell type (iii).

In pyramidal cells, depolarization from −95 mV and −45 mV led to a significant increase in membrane resistance and time constant values (one-way ANOVA, p < 0.001, n = 17–28; Fig. 7B,C). Resistance increased from 69.8 ± 31.9 MΩ to 155 ± 55.5 MΩ, p < 0.001; Fig. 7Ci), whereas membrane time constants increased from 3.6 ± 2.0 ms to 17.4 ± 6.39 ms (p < 0.001; Fig. 7Cii). Depolarization of interneurons also led to significant changes in membrane input resistance (one-way ANOVA, p = 0.01, n = 4–16), with values increasing from 165 ± 111 MΩ to 422 ± 145 MΩ; Fig. 7Di). All 16 interneurons in which resistance was quantified at different voltages expressed an increase in membrane resistance with depolarization. Likewise, membrane time constants increased from 6.2 ± 3.9 ms to 11 ± 3.7 ms (Kruskal–Wallis test, p = 0.001, n = 4–16; Fig. 7Dii). Note that our sample size at the most depolarized voltages was limited because some cells fired excessive action potentials at these voltages and were not included in the analysis. Therefore, both interneurons and pyramidal cells expressed an increase in membrane input resistance that was consistent with the increase in size of membrane voltage fluctuations with depolarization.

To determine whether the increase in membrane resistance was correlated with an increase in the SD of membrane voltage fluctuations within individual neurons, we plotted the normalized SD and membrane resistance values measured at different membrane voltages. For each dataset of SD and membrane resistance from an individual cell, the resistance and SD were normalized relative to their minimum values. As indicated for pyramidal cells (Fig. 7Ei) and interneurons (Fig. 7Eii), higher values of membrane resistance corresponded to higher values in membrane voltage SD. Between cells, however, larger membrane resistance values were not associated with larger fluctuations. Absolute membrane input resistance near rest (∼−75 mV) did not correlate with differences in membrane fluctuations size across the population of neurons (r² = 0.05; Fig. 7Eiii). Therefore, whereas changes in input resistance scaled with voltage fluctuation size within a cell, cells with larger input resistance did not necessarily express larger membrane voltage fluctuations.

As a result, the average ratio between resistance and SD was positive at each voltage and remained close to 1 in both cell types (one-way ANOVA, p = 0.94 for pyramidal cells, n = 10–12 and p = 0.99 for interneurons, n = 7 - 9; Fig. 7Fi, Fii). Further, the maximum average ratio (Ri/SD; Fig. 7Fiii) across measured voltages was close to 1 for pyramidal cells (1.12 ± 0.54, p = 0.44, n = 12) and interneurons (0.99 ± 0.35, p = 0.97, n = 9). Note that, although average values of the ratios were close to 1, ratios for individual cells varied between 0.5 and 2.5 (Fig. 7Fi, Fii), which indicates that changes in membrane resistance alone may not account for the increases in membrane voltage fluctuation size. Alternatively, the absence of a perfectly linearly relationship between resistance and SD in individual cells could be due to the large size of membrane fluctuations and steep voltage dependency of resistance; resistance at the peak and trough of a fluctuation may differ substantially from the mean resistance. Nonetheless, the relationship between input resistance and membrane trace SD was always positive and we never observed situations in which the slope was zero or negative.

Membrane and current fluctuations share similar spectral profiles in pyramidal cells and interneurons

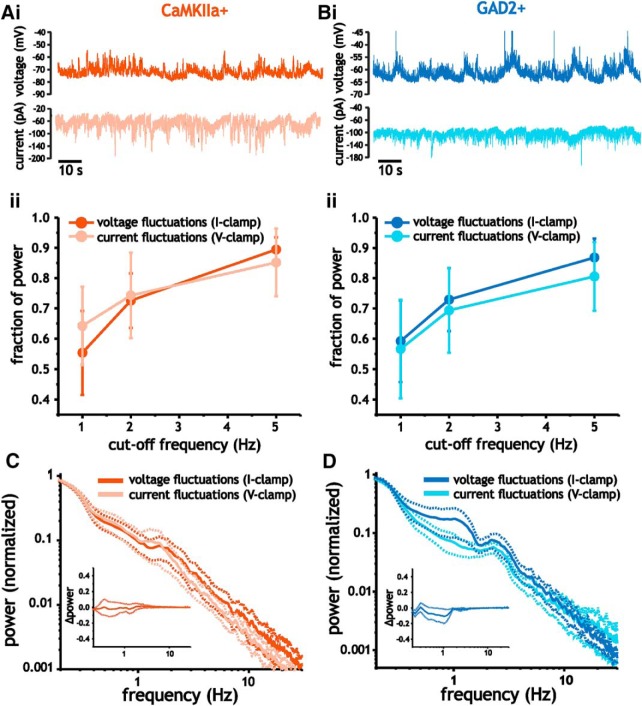
To address whether the frequency structure of membrane voltage fluctuations was a result of correlations in synaptic input or filtering by membrane capacitance, we compared the distribution of power in the spectra of voltage and current fluctuations acquired in current-clamp and voltage-clamp recordings, respectively, at similar voltages. As indicated previously in Figs. 5 and 6, both voltage and current fluctuations in pyramidal cells and interneurons were largely dominated by low-frequency power. In pyramidal cells, when compared at similar voltages (−60 mV to −80 mV), the cumulative power contained at <5 Hz, 2 Hz, and 1 Hz did not differ between voltage and current fluctuations (two-way ANOVA, p = 0.44, n = 7–20; Fig. 8Aii). Similarly, in interneurons, the distribution of power in both types of fluctuations were similar (two-way ANOVA, p = 0.12, n = 10–17; Fig. 8Bii).

Figure 8.

Voltage and current fluctuations express similar frequency content in pyramidal cells and interneurons. A, B, Example traces of membrane voltage (i, top) and current (i, bottom) fluctuations acquired in pyramidal cells (A) and interneurons (B), along with plots of average fraction of power at frequencies <5 Hz, 2 Hz, and 1 Hz (ii). C, D, Plot of average membrane current and voltage fluctuation spectra in pyramidal cells (C) and interneurons (D). Insets plots show difference in power (current–voltage spectra) as a function of frequency.

We also measured differences in voltage and current fluctuations recorded in the same cell to assess whether small differences could be detected. Consistent with our previous analysis, comparison of voltage and current fluctuations from the same cell showed similar spectra, with the difference in total power from 0.2 and 2 Hz between current and voltage fluctuations not differing significantly (pyramidal cells: Student's t test, p = 0.89, n = 5; interneurons: Wilcoxon signed-rank test, p = 0.56, n = 6; Fig. 8C, D, insets). The result is also consistent with measures of time constants (Fig. 7Cii, Dii); in both cells types and at different voltages, time constants were always small relative to the frequency content dominating voltage and current fluctuations. As a result, the spectra of membrane voltage fluctuations were largely inherited from the correlations in synaptic current inputs rather than any significant filtering associated with charging the membrane.

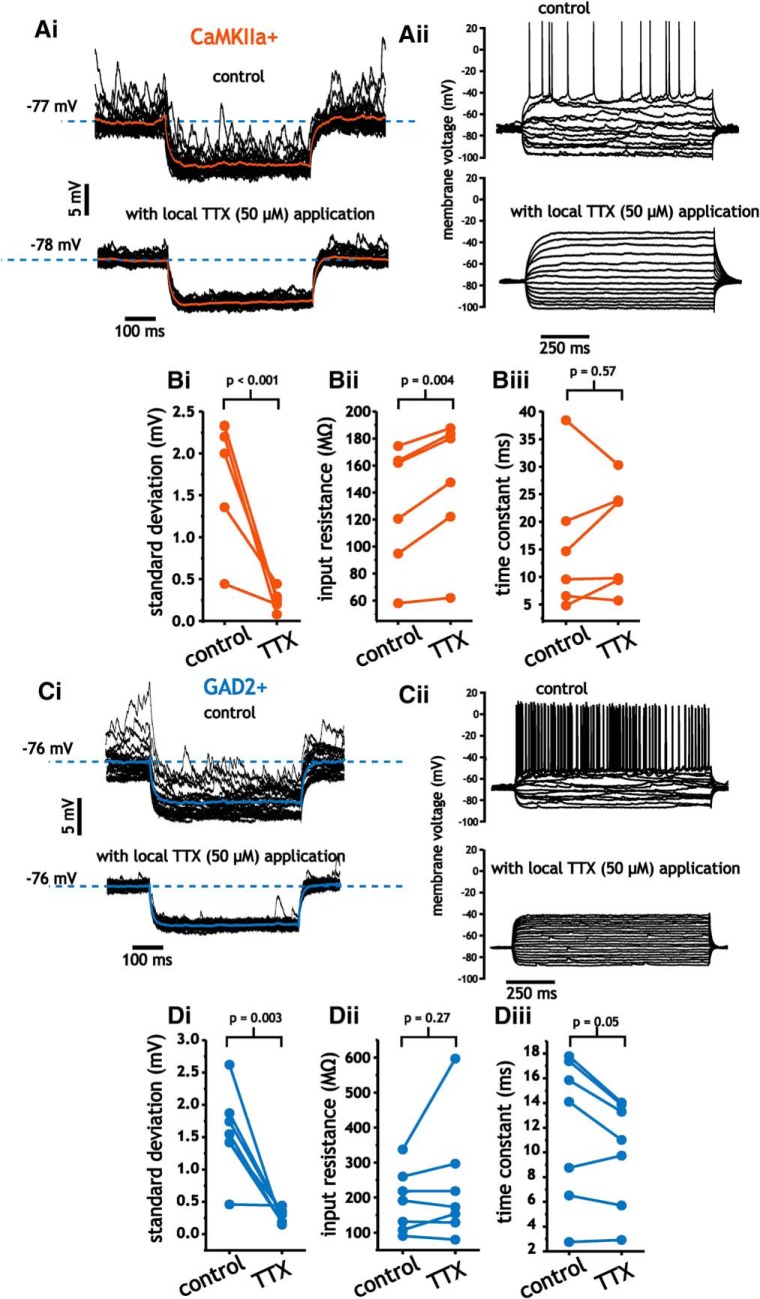
Eliminating membrane voltage fluctuations with TTX minimally alters membrane input resistance in pyramidal cells and interneurons

The inability of membrane time constant to influence the frequency structure of synaptic-mediated membrane voltage fluctuations could be related to a high conductance state brought on by intense synaptic activity; steady-state membrane input resistance and time constants are reduced by a large increase in input conductance from synaptic inputs. If so, then the reduction or elimination of synaptic activity would significantly increase both membrane input resistance and time constant values.

To test this, we delivered TTX (50 μm) through a secondary pipette located near the recording pipette (∼100–200 μm away) using a gradual increase in positive pressure. Using this approach, we were able to block synaptic-mediated voltage fluctuations associated with awake recording conditions. By measuring input resistance using small hyperpolarizing steps (5–10 mV) near resting potentials from the same cell before and after the application of TTX, we could measure the impact of synaptic inputs on average membrane conductance at the cell body.

Within minutes of TTX application, the SD of membrane voltage fluctuations was decreased in pyramidal cells (1.78 ± 0.75 mV vs 0.25 ± 0.12 mV, paired Student's t test, n = 6, p < 0.001; Fig. 9Ai,Bi). The application of TTX led to a small, but significant change in membrane input resistance (129 ± 46.1 MΩ vs 147 ± 48.9 MΩ, paired Student's t test, p = 0.004; Fig. 9Bii). This change, however, amounts to an ∼1 nS (1/147 MΩ = 6.8 nS vs 1/129 MΩ = 7.8 nS) difference in membrane conductance between the two conditions. Consistent with the small change in membrane resistance, time constants were not significantly altered by the elimination of voltage fluctuations (15.7 ± 12.5 ms vs 17.1 ± 10.0 ± ms, paired Student's t test, p = 0.57; Fig. 9Biii).

Figure 9.

Block of spike-generated synaptic input fluctuations with TTX minimally alters membrane input resistance and time constant values in layer 2/3 pyramidal cells and interneurons. A, Example trace of pyramidal cell membrane voltage in response to step hyperpolarizations before (i, top) and after (i, bottom) TTX application, along with example traces indicating a lack of spike generation with TTX (ii). B, Plots of SD (i), membrane input resistance (ii), and time constant (iii) before and after the application of TTX. C, Example trace of interneuron membrane voltage in response to step hyperpolarizations before (i, top) and after (i, bottom) TTX application, along with example traces indicating a lack of spike generation with TTX (ii). D, Plots of SD (i), membrane input resistance (ii), and time constant before and after the application of TTX.

As in pyramidal cells, application of TTX in interneurons drastically reduced the SD of membrane voltage fluctuations (1.58 ± 0.65 mV vs 0.27 ± 0.11 mV, paired Student's t test, n = 7, p = 0.003; Fig. 9Ci,Di). Despite this, neither membrane input resistance (191.1 ± 10.1 MΩ vs 235.5 ± 173 MΩ, paired Student's t test, p = 0.27; Fig. 9Dii) nor time constant (11.9 ± 5.9 ms vs 10.1 ± 4.3 ms, paired Student's t test, p = 0.05; Fig. 9Diii) values were significantly affected. Note, portions of the dataset regarding TTX application in pyramidal cells (five of the six datasets for SD, input resistance, and time constant) have been previously published by our group (Fernandez et al., 2018).

Average resting potential before and after TTX in pyramidal cells was −71.3 ± 3.8 mV and −72.1 ± 5.9 mV (n = 6, p = 0.44, paired t test), respectively. For interneurons, resting values were −72.1 ± 5.2 mV and −72.2 ± 7.2 mV (n = 7, p = 0.97, paired t test). Therefore, the minimal impact of TTX on input resistance was not related to changes in membrane voltage. These results indicate that steady-state input resistance and time constant values are minimally affected by the ongoing synaptic events associated with spontaneous activity. Accordingly, the amplification of membrane voltage fluctuations with depolarization reflects an intrinsic property of neurons that is independent of background synaptic activity, whereas the frequency content largely arises from correlations in synaptic input.

Discussion

Synaptic input fluctuations are influenced by voltage-dependent changes in intrinsic membrane input resistance

Both pyramidal cells and interneurons expressed a voltage-dependent increase in membrane input resistance. Although the membrane time constant also increased with depolarization, values remained small (<20 ms) and are unlikely to contribute to the filtering of extremely slow membrane voltage fluctuations. The long correlation timescale and low-frequency power expressed in voltage fluctuations therefore likely reflect correlations in synaptic inputs, whereas the amplitude is set by a combination of voltage-dependent intrinsic membrane properties and the size of synaptic current fluctuations. Further, measures of input resistance with local TTX application indicate that synaptic inputs generated during spontaneous activity in awake somatosensory cortex of mice induce small changes in cell body membrane resistance. Even during periods of whisking, changes were significant but small. Overall, these results indicate that activity in layer 2/3 neurons of somatosensory cortex associated with awake states is characterized by synaptic input with low-frequency power and a low-conductance state in which intrinsic membrane properties can significantly influence the size of voltage fluctuations.

Comparison with previous in vivo recordings

Spontaneous activity during awake states can potentially include many substates associated with different levels of arousal that change the frequency content of membrane voltage fluctuations. For example, states of high arousal and whisking are associated with higher frequency content in the power spectrum of membrane voltage traces (Crochet and Petersen, 2006; Reimer et al., 2014; McGinley et al., 2015a,b). Consistent with this, we found that whisking decreased low-frequency power and the skewness coefficient of membrane voltage fluctuations. In our recordings, however, these moments represented ∼8% of the total duration of the voltage traces. For this reason, the average spectra and skew of the nonwhisking states were similar to the average values acquired from the total duration.

Cortical membrane voltage histograms under anesthesia often express a bimodal distribution resulting from two reoccurring and clearly discernible transition states (Destexhe and Paré, 1999; Haider et al., 2006; Waters and Helmchen, 2006). Although we observed histograms of membrane voltage traces with positive skews, which can result from a bimodality in the histogram, pyramidal cells and interneurons consistently expressed unimodal distributions as determined using Hartigan's dip test. This is similar to previous recordings under quiet and awake conditions from rodents and monkeys from different cortical regions (Crochet and Petersen, 2006; Okun et al., 2010; Hromádka et al., 2013; Tan et al., 2014).

These conditions are also associated with synchronous activity in the LFP and are speculated to be associated with a low conductance state (Tan et al., 2014). In contrast, desynchronized LFP activity resulting from active sensory processing is associated with more depolarized intracellular membrane voltage, lower membrane resistance, and histograms with Gaussian distributions (Crochet and Petersen, 2006). Consistent with this interpretation, we observed changes in the spectra and statistics consistent with previous findings. Although we only observed modest differences in membrane input resistance associated with whisking or blocking synaptic activity, the size of these changes are also similar to those in previous studies during whisking in somatosensory cortex (Crochet and Petersen, 2006).

Potential causes for changes in intrinsic membrane resistance

Most commonly, an increase in subthreshold membrane input resistance with depolarization results from the activation of Na⁺ conductance (Schwindt and Crill, 1977; Fernandez et al., 2007, 2015; Branco et al., 2016). The negative slope of the Na⁺ current I–V curves leads to a counterintuitive increase in apparent input resistance as membrane voltage is depolarized across the subthreshold region. Recently, this property has been shown to set the integration of synaptic inputs in hypothalamic cells in vivo (Branco et al., 2016), as well as those associated with place cell activity in hippocampal pyramidal cells (Lee et al., 2012; Hsu et al., 2018). As an alternative, voltage-gated K⁺ currents also provide a mechanism for the decreased input resistance at hyperpolarized voltages. For example, the decrease in resistance at hyperpolarized voltages that we observed could be due to activation of K_ir channels, which can be opened by GABA_B receptors (Dutar and Nicoll, 1988). An increase in resistance with depolarization has only been reported in a few different types of neurons. In our recordings, however, the majority of pyramidal cells and interneurons expressed an increase in resistance with depolarization. Accordingly, the ubiquitous nature of this observation suggests a possible neuromodulatory mechanism that affects multiple different types of neurons similarly.

It is important to note, however, that the interaction between changes in intrinsic membrane resistance and synaptic input is unlikely to be a straightforward amplification. As indicated, periods of whisking induce different forms of membrane voltage fluctuation statistics that cannot be reproduced by simply depolarizing neurons. Nevertheless, the increase in input resistance is an intrinsic property of the cell that will interact with synaptic or neuromodulatory inputs.

Quiet and awake states in mouse somatosensory cortex are associated with a “low-conductance” state

Up-states recorded in deeper layers of cortex under anesthesia in ferrets and cats have been shown to result from large increases in mean excitatory and inhibitory synaptic conductance that is comparable in size to the intrinsic neuronal membrane conductance (Paré et al., 1998; Destexhe and Paré, 1999; Destexhe et al., 2003; Hasenstaub et al., 2005; Haider et al., 2006). Likewise, under awake conditions, intracellular recordings in cat association cortex have also indicated high levels of approximately balanced synaptic activity (Rudolph et al., 2007). In contrast, our measures of input resistance before and after TTX application, as well as during whisking, indicate a small contribution from synaptic inputs to cell body membrane conductance in both pyramidal cells and interneurons.

Consistent with our results, Waters and Helmchen (2006), using whole-cell patch recordings in rat somatosensory layer 2/3 pyramidal cells, found that up-states are generated by sparse synchronous volleys of excitation with little inhibition that generate a small conductance change at the cell body (Waters and Helmchen, 2006). Our results here, as well as those of others comparing input resistance between quiet/idling states and active whisking in mice (Crochet and Petersen, 2006), have shown significant but small changes in average membrane conductance (<3 nS) underlying depolarizations in somatosensory cortex. Therefore, it may be that species, as well as cortical region and depth, influence the mean intensity of spontaneous activity and the generation of a high-conductance state.

Voltage fluctuations express low-frequency power and long correlation times

Previous intracellular recordings in layer 2/3 pyramidal cells and interneurons have shown that spontaneous activity in awake rodents is characterized by low-frequency power (Crochet and Petersen, 2006; Poulet and Petersen, 2008; Constantinople and Bruno, 2011; Bennett et al., 2013). Our recordings, however, point to even slower fluctuations than those measured previously. Autocorrelation and spectral analyses revealed membrane voltage fluctuations with durations as long as 10 s and with 75–90% of power <5 Hz. The slower timescale observed in our recordings is most likely due to our use of longer traces (10 s windows and 2-min-long traces) in our analysis than those used in previous studies (Hasenstaub et al., 2005; Crochet and Petersen, 2006; Poulet and Petersen, 2008; Bennett et al., 2013). Interestingly, data from humans using measures of LFPs also indicate extremely long correlation timescales and power spectra with 1/f scaling during spontaneous activity associated with idling (Nir et al., 2008).

Potential issues with voltage-clamp and dendritic contributions to voltage fluctuations

Although our voltage clamp could have been arguably improved using internal cesium chloride in the intracellular pipette solution, we found that replacing internal K⁺ with cesium led to membrane resting values near −10 mV, which made voltage clamping cells at voltages between −95 mV and −45 mV more difficult due to the substantial increase in mean current required to clamp cells near these voltages. This is expected and results from reducing internal K⁺ concentration with cesium and the resulting change in the K⁺ reversal potential (Fleidervish and Libman, 2008). Furthermore, in our experience, as well as others (Kato et al., 2017), the use of QX-314 in the pipette solution significantly reduces synaptic-mediated spontaneous membrane voltage fluctuations during in vivo patch recordings. The use of cesium chloride and ion channel blockers has also been shown to provide minimal benefits in resolving space clamp issues and measures of synaptic currents far from the cell body (Williams and Mitchell, 2008).

More recently, direct measures of synaptic conductance near the spine on dendrites provide further evidence that voltage clamp at the soma severely underestimates synaptic conductance values (Beaulieu-Laroche and Harnett, 2018). Therefore, the results from our study and others are limited to measures of resistance, current, and voltage at or near the cell body. This also includes our measures of membrane input resistance in pyramidal cells and interneurons acquired in current clamp. Any accurate measure of synaptic input conductances originating at the dendrites will require voltage clamping at or near the origin in the dendritic branch (Williams and Mitchell, 2008; Beaulieu-Laroche and Harnett, 2018).

It is thus possible that dendritic filtering and nonlinear amplification from dendritic, voltage-gated channels also contribute to the low-frequency content of membrane voltage fluctuations. Although we cannot rule out dendritic filtering, dendritic recordings in vivo indicate that the slower, larger depolarizations associated with sensory input are amplified by NMDA receptors (Smith et al., 2013). Further, dendritic recordings indicate fluctuations with a similar frequency content to those recorded at the cell body (Smith et al., 2013). These findings indicate that slower events are shaped by synaptic receptor kinetics and that dendritic filtering is unlikely to affect the low-frequency content of these events.