THREE AUTHORS REPLY

We thank McSkimming et al. (1) for their comments on our paper (2), which provide an opportunity for us to expand the discussion of quantification of temporal instability of the human microbiome and the implications for large-scale prospective epidemiology studies.

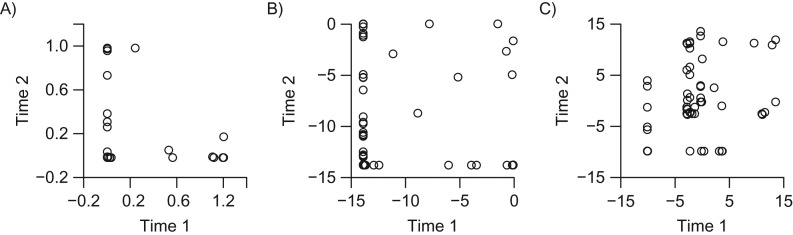
In our original paper (2), we reported relatively low intraclass correlation coefficients (ICCs) for phylum-level relative abundance (RA) data from the Human Microbiome Project (HMP) (3, 4). McSkimming et al. reported much higher ICC values after centered log-ratio (CLR) transformation (5). Building upon this, we developed a data-generative model to investigate whether CLR improved ICC values only for the HMP data or consistently for other scenarios. To proceed, we assume that the underlying long-term RA composition vector for $K$ taxa is $\mathrm{\Lambda }=({\mathrm{\lambda }}_1,\cdots ,{\mathrm{\lambda }}_K)$. The time-specific RA vector $P_t=(p_{t1},\cdots ,p_{tK})$ follows a Dirichlet distribution $D({\mathrm{\theta }\mathrm{\lambda }}_1,\cdots ,{\mathrm{\theta }\mathrm{\lambda }}_K)$. Here, the parameter $\mathrm{\theta }$ models the over-time instability, with a large value of $\mathrm{\theta }$ implying smaller variability and thus a higher ICC. We used this model to simulate RA vectors for 1,000 subjects at 2 time points to evaluate ICC numerically. We found that naive RA estimates without transformation typically had the lowest ICC values and that CLR transformation consistently improved ICC for individual taxa, particularly for rare taxa. In Figure 1, using the naive estimate for uncommon taxa (average RA = 1.2%), the ICC is practically zero; log transformation modestly improves ICC; CLR improves ICC to 0.83. While it is mathematically very complicated, if not impossible, to explicitly derive a formula for ICC after CLR, numerical examination suggested that the high value of ICC after CLR was driven primarily by other, more common taxa that have relatively high ICC values.

Figure 1.

Intraclass correlation coefficient values for an uncommon taxon using naive estimates of relative abundance (RA) vector (A), log transformation (B), and centered log-ratio transformation (C). The RA vectors at 2 data points for 1,000 subjects were generated for 5 taxa based on the data generative model with Λ = (0.1,1,1,1,5) and θ = 0.1 (suggesting large over-time instability). The average RA for the first taxon is 0.1/(0.1 + 1 + 1 + 1 + 5) = 1.2%.

The motivation for calculating ICC metrics is to evaluate the temporal-instability power loss to detect associations. More specifically, an ICC value is relevant only to the specific disease model. If the risk of developing a disease depends linearly on the RA of a taxon, the relevant ICC should be evaluated using the naive RA of the taxon. If the disease risk depends on log(RA), the relevant ICC should be evaluated using the log-transformed RA. The observed high ICC after CLR transformation in the HMP data would suggest a potentially small power loss due to over-time variability. However, effect size change due to the CLR transformation is another important factor that affects statistical power. CLR-based ICC might be overly optimistic for power estimates if effect-size change is ignored. Thus, careful investigation of transformation is warranted under different disease models by jointly considering ICC and effect sizes. Given that very few prospective studies have been performed to suggest an unambiguous disease model, we would recommend evaluating ICCs under different transformations that do or do not consider the compositional feature of the microbiome (i.e., log transformation, CLR (5), and isometric transformation (6), as was suggested by McSkimming et al. (1)). In conclusion, transformation of microbiome data should be compatible not only with compositional structure of the data but also with the postulated disease model.