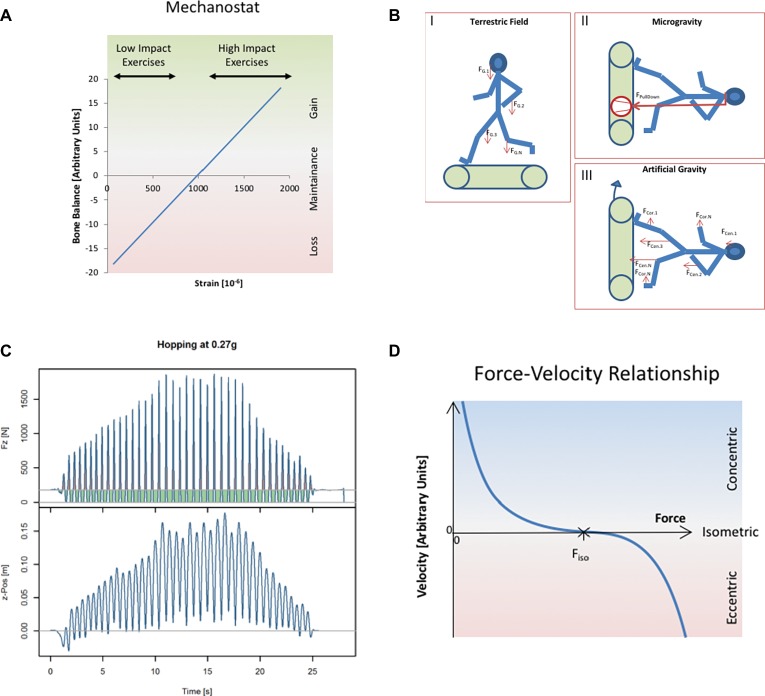
Figure 1.

(A) Conceptualizationthe effect that tissue strains have on adaptive processes. This concept is well known in the bone field as “mechanostat” (Frost, 1987a), and it seems in principle to apply also to tendon, muscle, and likely other tissues. The mechanostat concept considers tissue’s mechanoadaption as a negative feed-back system, analogous to a thermostat. While thermostats enable constancy of temperature, the mechanostat keeps the tissue strains constant by adding or removing material in response to altering forces. Material evidence for the mechanostat concept had been provided by Rubin and Lanyon (1987), whose data are exemplified in the present diagram. Exercise-induced tibial compression strains are taken from Milgrom et al. (2000a,b) (low impact exercises, walking and bicycling; high impact exercises, running and drop jumps from different heights). (B) Different strategies to replace gravity by artificial pull-down forces. (I) Pull-down in the Earth’s gravitational field is a result of the body’s weight, which can be conceptualized as a homogeneous vector field within the entire body. (II) In microgravity, pull-down forces are generated by, e.g., pneumatic systems or bungees, and they are applied to the body via interfaces at the shoulders or hips. This “force concentration” is illustrated by size and thickness of the vector. (III) Artificial gravity replaces gravitational acceleration by centrifugal centrifugation. This avoids the problem of force application. However, it leads to in-homogeneity of the gravitational field (indicated here by different sizes of vectors) and generation of Coriolis forces, both of which become more pronounced with shorter radius of centrifugation. (C) Illustration of the time course of ground reaction forces during hopping, exemplified here for hopping during hypogravity simulation at g = 0.27 (first published in Weber et al., 2019). The vertical elevation of the body’s center of mass (z-position, lower panel) demonstrates that hops of increasing height are associated with increasing vertical ground reaction forces (Fz, upper panel). Green areas denote periods where Fz < weight (i.e., downward acceleration), and the red areas denote periods where Fz > weight (upward acceleration). Since no vertical net movement had occurred at the end of the hopping trial, the green and red areas are of equal size. Effectively, by fractioning the static load into “duty cycles,” one can produce ground contact forces that exceed the static loading force. The diagram therefore illustrates how jumping exercises can generate peak Fz that are substantially greater than static bodyweight. (D) The muscle’s working diagram, which also is known as “Hill’s” curve, is describing the force-velocity relationship of maximally activated muscle. In concentric mode, the muscle is shortening (v is positive) because the resistive force is smaller than the muscle’s contractile force. In isometric mode, resistive force and contractile force are equal, and v = 0. In eccentric mode, the resistive force exceeds the contractile force, and the muscle is lengthening (negative v). The force-velocity relationship is empirically described by a hyperbolic function (Hill, 1938).