Figure 2.

Noise Is Reduced Exponentially with Mechanical Coupling

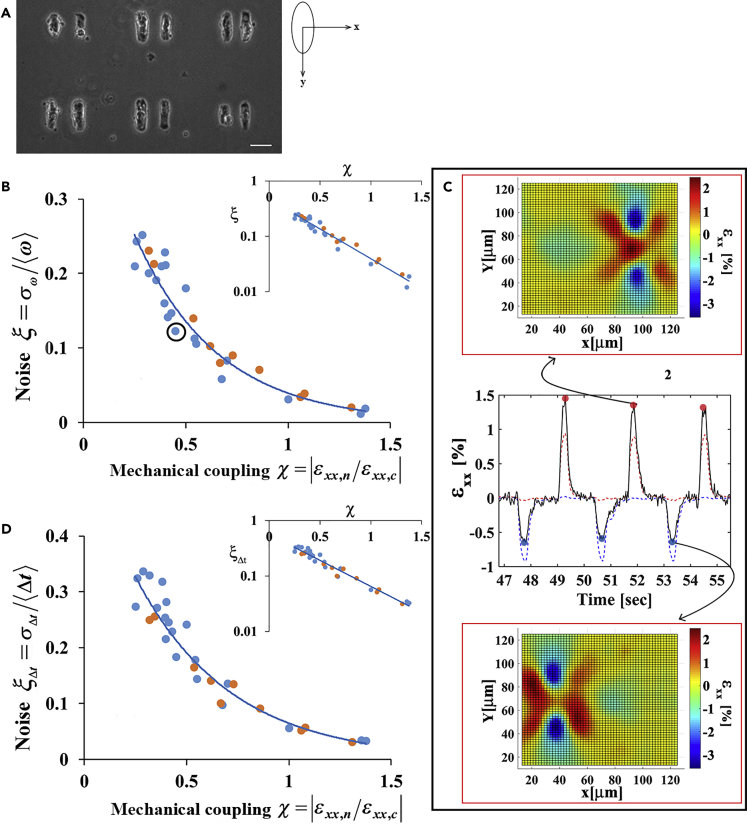
(A) A representative image of isolated pairs of cardiac cells on a pattern. Notice that there is no physical contact between the cells. Scale bar is: 50 μm. We use an axis system whereby the cells are aligned along the y axis. Using this coordination system, the contraction axis of the cell (the long axis) is the y axis and the x axis is the direction of the vector connecting the two cells. A beating cardiac cell generates deformations on a flexible substrate in the x-direction, in addition to the ones in the y-direction owing to the Poisson's effect.

(B and D) Beating noise decays exponentially with the strength of mechanical coupling to a neighboring cell. Beating noise, defined as the relative SD of the beating frequency (B) or as the relative SD of the time between consecutive beatings (D), is plotted as a function of mechanical coupling. The insets in (B) and (D) show the noise in a logarithmic scale. The decay constant in (B) and (D) is 2.43 ± 0.19 and 2.2 ± 0.14, respectively. SDs were calculated using the bootstrap method. The predictive power of the model was assessed using leave-one-out cross-validation. For both (B) and (D): the blue and orange circles represent cells that were cultured on 4 kPa and 1 kPa substrates, respectively. n = 30 cells are shown from 8 different cultures and 16 different dishes. R² values for A and B are reported in Table S1 in the Supplemental Information.

(C) Demonstration of the calculation of mechanical coupling for a representative pair of beating cardiac cells (the point marked in [B], for additional details see Figure S2). In short, the black curve shows the average strain at the edge of the beating cell in the x-direction. The blue and red curves are the normalized beating signals of the left and right cells, respectively, for a short time period in which the cells beat in anti-phase and are only shown to mark the time position of cell contraction. The strain peaks marked with red dots result from contractions of the right cell, whereas the strain peaks marked with blue dots result from contractions of the left cell. Therefore, mechanical coupling for the right cell is calculated as χ_R = |ɛ_xx,L(x = R)/ɛ_xx,R(x = R)|, i.e., by dividing the average strain values generated by the left cell at the edge of the right cell (blue dots) by the average strain generated by the right cell next to its edge (red dots). Since the strain generated by the right cell next to its edge is positive, whereas the strain generated by its neighbor is negative, we use the absolute value of this ratio. Strain maps at two time points are shown.