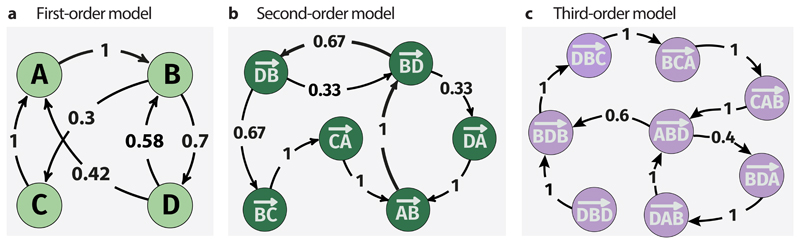
Figure 5. De Bruijn graphs with m dimensions help generalise network analytic methods to higher-order models.
(a) shows a first-order model with dimensionality m = 1 for a set of observed causal paths between four nodes A, B, C, and D. (b) shows a second-order model with m = 2 and (c) shows a third-order model with m = 3. Starting from a a first-order network model, higher-order models can be generated by an iterative line graph construction. The absence of transitions that correspond to a possible transitive path in the underlying first-order network, such as indicates constraints in the observed paths that change the causal topology of the system.