Abstract
Artificial Neural networks (ANNs) are often applied to data classification problems. However, training ANNs remains a challenging task due to the large and high dimensional nature of search space particularly in the process of fine-tuning the best set of control parameters in terms of weight and bias. Evolutionary algorithms are proved to be a reliable optimization method for training the parameters. While a number of conventional training algorithms have been proposed and applied to various applications, most of them share the common disadvantages of local optima stagnation and slow convergence. In this paper, we propose a new evolutionary training algorithm referred to as LPSONS, which combines the velocity operators in Particle Swarm Optimization (PSO) with Mantegna Lévy distribution to produce more diverse solutions by dividing the population and generation between different sections of the algorithm. It further combines Neighborhood Search with Mantegna Lévy distribution to mitigate premature convergence and avoid local minima. The proposed algorithm can find optimal results and at the same time avoid stagnation in local optimum solutions as well as prevent premature convergence in training Feedforward Multi-Layer Perceptron (MLP) ANNs. Experiments with fourteen standard datasets from UCI machine learning repository confirm that the LPSONS algorithm significantly outperforms a gradient-based approach as well as some well-known evolutionary algorithms that are also based on enhancing PSO.
Keywords: Computer science
1. Introduction
Artificial Neural Networks (ANNs) are inspired by the human nervous systems and often used for pattern recognition and data classification [1] in various application domains such as manufacturing and medical diagnostics [2], [3], [4], [5], [6]. One type of ANNs is Multi-Layer Perceptron (MLP), which is particularly useful for nonlinear modeling through training algorithms that are either gradient-based or based on meta-heuristics [7]. One of the well-known gradient-based methods is Back Propagation (BP), which however can get trapped into local minima and cannot find the appropriate values for the control parameters of weight and bias using training algorithms especially when the problem has a large scale [8]. This limitation has inspired researchers to harness meta-heuristic approaches to train ANNs as their stochastic nature contributes to remarkable performance in finding global optimal results [9]. One of the well-known meta-heuristic training algorithms is Particle Swarm Optimization (PSO) [10], a swarm intelligence-based algorithm inspired by the social behavior of animals such as birds flocking and fishes schooling. Each fish or bird is treated as a particle that has position and velocity and particles try to follow their local best positions until they reach the global best position. PSO, including its extensions such as Ant Colony Optimization (ACO) and Artificial Bee Colony (ABC), has been employed in various studies to train their MLP ANNs and showed great performance in optimizing the training process [11], [12], [13].
A weak trade-off between exploration and exploitation and limitation of population diversity are two major challenges in PSO [14] and work has been done to address them in terms of parameter setting, neighborhood topology, learning approaches, and hybridized methods [15]. For example, some works tried to fine tune and regulate the parameters through memory adaptation [16], [17], Gaussian adaptation [18], or fuzzy-based methods [19], while other works attempted to avoid premature convergence by utilizing a neighborhood strategy like fully informed [20], self-adaptive [21] or ring topology [22], or a combination strategy through Lévy distribution such as LFPSO [23] and PSOLF [24]. The No Free Lunch (NFL) theorem asserts that no optimization methods can defeat all optimizers in solving all problems [25], [26], which motivated us to further extend PSO in order to better avoid local minimum and create a more balanced trade-off between exploration and exploitation in training MLP ANNs.
The proposed PSO extension is a hybrid algorithm that combines the PSO velocity operator with the Mantegna Lévy distribution to escape from local minima by finding different search areas, and to promote global search, enhance convergence speed, and balance exploration and exploitation by dividing the population and generation between different sections of the algorithm. The proposed hybrid algorithm further combines the Mantegna Lévy distribution with a new formulation of Global Neighborhood search [14] to boost local search, mitigate premature convergence and avoid local minima by searching more undiscovered areas in the search space to produce more diverse solutions. The new hybrid algorithm is referred to as LPSONS (Mantegna Lévy Flight, Particle Swarm Optimization, and Neighborhood Search) and has been implemented to optimize training of Feedforward MLP ANNs with a single hidden layer for the sake of simplicity yet without losing generality as the single layer can be generalized to approximate any continuous function with a finite number of neurons [27]. We have also conducted a series of experiments to analyze and test the structure schema of the proposed algorithm with fourteen datasets from UCI machine learning repository. We have further evaluated the performance of LPSONS against those of two well-known PSO extensions – PSOLF and LFPSO – and a well-known Gradient-Based algorithm Back Propagation (BP) [28] based on the metrics of Classification Accuracy, Mean Squared Error (MSE), Specificity and Sensitivity. Statistical results using Friedman test show that the LPSONS algorithm significantly outperforms those benchmark algorithms.
The rest of the paper is organized as follows. Section 2 introduces some related work on training of ANNs and the fundamental work on which the proposed approach is based including MLP networks, Particle Swarm Optimization, and Lévy Flight. Section 3 then provides the details of the proposed LPSONS algorithm and after that Section 4 presents the evaluation experiments and discusses the results. Section 5 finally concludes the paper with a summary of major contributions and future work.
2. Related work
2.1. Training of artificial neural networks
In recent years, quite a lot of work has been done to optimize the training of ANNs using evolutionary algorithms, especially Evolution Strategy, Differential Evolution, and swarm-intelligent based approaches [17], [18], [19], [20]. Green II et al. proposed a Central Force Optimization (CFO) method for training ANNs and found it performed better than PSO in terms of algorithm design, computational complexity, and natural basis [29]. Bolaji et al. proposed the fireworks algorithm and compared it against other established algorithms using different benchmark datasets [30]. Faris et al. proposed the Lightening Search Algorithm (LSA) for finding optimal results and tested it with different measurements [28]. Karaboga et al. contributed Artificial Bee Colony (ABC) for optimizing weights in ANNs [31]. Aljarah et al. developed the whale optimization algorithm to find optimal connection weights in MLP ANNs [32], which showed superior performance to those of other benchmark algorithms.
Genetic Algorithm (GA) has been applied to different problems including training of MLP ANNs. For instance, in Sexton et al.'s work [33], GA was used to optimize an MLP ANN with a single hidden layer. Karegowda et al. proposed a hybrid approach combining GA and Back Propagation Network (BPN) to optimize connection weights in ANNs and applied their work to medical diagnosis [34]. Khan et al. did a comparison study between two gradient descent algorithms and three population-based algorithms including GA, PSO, and Bat algorithm and found that the Bat algorithm performed the best [35]. Pawelczyk et al. proposed a Genetically-Trained Deep Neural Networks in order to promote the training process in Deep Neural Networks (DNN) by combining genetic algorithm and Gradient-based Back Propagation algorithm [36].
A number of hybrid algorithms have been proposed to improve the performance of PSO for training ANNs. Chen et al. suggested a hybrid approach to optimizing the training of Feedforward Neural Networks (FNNs) by combining PSO and Cuckoo Search (CS) and the comparison results revealed that it outperformed either PSO or CS alone as well as other FNN training algorithms [37]. Mirjalili et al. proposed a hybrid method using PSO and Gravitational Search Algorithm (GSA) for training FNNs and the comparison results showed its superior performance to that of the basic PSO and GSA alone in terms of convergence speed and local minima avoidance [38]. Ozturk and Karaboga introduced a hybrid approach consisting of ABC and the Levenberq-Marquardt (LM) algorithm for training an ANN [39] in which the network is first trained by the ABC algorithm and the LM algorithm then continues the training by grasping the best weight set of ABC algorithm in order to minimize the training error [39]. The proposed approach was tested on XOR, Decoder-Encoder, and 3-Bit Parity problems and exhibited remarkable performance.
In summary, evolutionary algorithms are proven useful in training MLP ANNs and much work has been done to enhance their performance from different perspectives using different measures such as training error and accuracy of classification. Our work in this paper extends Particle Swarm Optimization with Mantegna Lévy Flight and Neighborhood Search in order to produce more diverse solutions, mitigate premature convergence and avoid local minima using a rich set of measurement metrics including Classification Accuracy (ACC), Mean Squared Error (MSE), Specificity and Sensitivity.
2.2. Multi-layer perceptron networks
An Multi-Layer Perceptron (MLP) network contains the elements of input layer, hidden layer, and output layer [40]. An MLP network can contain multiple different hidden layers enabling the network to have computational and processing abilities to generate the network outputs [41]. Figure 1 shows an MLP network with a single hidden layer, which contains some weights connecting between layers. The output values will be calculated through the following steps.
Figure 1.
An MLP network with a single hidden layer.
First, the sum of weights is calculated as follows:
| (1) |
where is the input variable, is the weight between the input variable and neuron j, and is the input variable's bias term.
Second, neurons' output values in the hidden layers are generated from the received values of weighted summation (Equation (1)) by using an activation function. A popular choice of such a function is a sigmoid function as follows:
| (2) |
where is the sigmoid function for neuron j and is the sum of weights.
Finally, the output of neuron j is calculated as follows:
| (3) |
where is the output of neuron j, is the weight between the output variable and neuron j, is the activation function for neuron j, and is the output variable's bias term.
After the structure of an MLP ANN is created, a training process is required to fine tune the control parameters of weight and bias in order to achieve good results, e.g., minimizing the error rate including both classification and approximation errors. Both gradient-based approach such as BP and meta-heuristic-based approach such as PSO can be used for this purpose. Our proposed training algorithm is based on PSO.
2.3. Particle Swarm Optimization (PSO)
Particle Swarm Optimization (PSO), a swarm intelligence based algorithm proposed by Kennedy and Eberhart [10], mimics the social behavior of birds or fishes such as flocking or schooling, regrouping, and changing directions suddenly by using velocity to model their movements. In PSO, each solution is called a particle, which is characterized by four attributes: the current position , the best historical position evaluated by the objective function , the best historical position discovered in all particles , and the current velocity . Changes of velocity and position are described by the following equation:
| (4) |
where and are acceleration factors, w is inertia weight, and and uniformly generate random numbers in the range of [0, 1]. Algorithm 1 lists the pseudo code of the PSO algorithm.
Algorithm 1.
Particle Swarm Optimization (PSO).
2.4. Lévy flight
In nature, animals look for food based on a random walk, that is, the next step in a search path is based on the current location and the transition probability to the next location. A Lévy flight is a kind of random walk and studies have shown that many animals and insects have their flight styles resemble the features of Lévy flights. This behavior has been applied to optimal search and optimization algorithms [42], [43], [44]. In particular, transition from to in the ith solution of an optimization algorithm can be described as follows:
| (5) |
where ∂ is the step size that is subject to the scale of the problem of interest, ⊕ is the product operator for entry wise multiplications [42], and provides a random walk with their large steps drawn from a Lévy distribution as follows:
| (6) |
which has an infinite variance with an infinite mean and . Clearly, generation of step size samples is not trivial using Lévy flights and below is a simple scheme [43]:
| (7) |
where μ and v are drawn from normal distributions and are defined as follows:
| (8) |
where Γ is the standard gamma function.
3. Methodology
This section provides the details of the proposed LPSONS algorithm, including the division strategy that splits the population and the generations so that partial values of the population and the generations are assigned to different components of the proposed algorithm, the Mantegna Lévy distribution and PSO operators, the Neighborhood Search method, and the encoding strategy.
3.1. Division strategy in population and generations
The division strategy aims to divide the population and the generations and assign them to different components of the algorithm. Some evolutionary algorithms benefit from a division strategy in population as well as one in generations. For instance, Zhang et al. introduced a CS algorithm that utilized subgroups of the population and experimental results showed that the adopted division strategy not only helped improve both exploration and exploitation but also create a balance between them [45]. Salgotra et al. proposed an efficient hybrid algorithm based on CS and Cauchy Distribution by dividing both the population and generation in order to improve exploration and exploitation and tested the algorithm with varying population sizes using some benchmark problems [46].
It has been proved that a good balance between exploration and exploitation is a key efficiency indicator of an evolutionary algorithm, especially a swarm intelligence-based algorithm. Good exploration prevents from getting into local minima, while good exploitation suggests efficient convergence speed [47]. Therefore, the proposed LPSONS algorithm also uses a division strategy for both population and generations in order to strike a good balance between exploration and exploitation. In the proposed algorithm, both the population size and the generations size (total number of generations in proposed algorithm) are divided into two parts: one half is used by the Mantegna Lévy distribution along with the PSO operator, while the other half is used by both the Mantegna Lévy flight and PSO operator as well as the global neighborhood search strategy in order to obtain the fitness value. In addition, in order to prevent from premature convergence, if the fitness value of generated solutions does not change for a number of iterations, the algorithm switch its approach with another one to generate new solutions. These values utilized two variables such as Limit value and Trial value. The limit value is the constant number of iterations which is defined inside the loop related to the population size and Trial is a counter. When the trial values exceed the limit value, the algorithm uses another strategy to generate solutions. This strategy is inspired by Haklı et al.'s work in which a limit value was set to change the solution generating strategy when there was not enough change in producing better solutions [23].
3.2. Mantegna Lévy distribution and PSO operators
The LPSONS algorithm employs Mantegna Lévy distribution along with PSO velocity operator in order to improve its accuracy. Based on [48], [49], Mantegna Lévy distribution is defined as follows.
| (9) |
where is a generated solution by the Mantegna Lévy flight, α indicates the Lévy step size, φ is computed using Equation (8) which equals to , =φ⋅ and ( is a normal distribution of D dimension with ), and is a randomly selected solution, while is the best solution ever found. The step size α is defined based on the following equation.
| (10) |
In the proposed LPSONS algorithm, a solution will first be generated using Mantegna Lévy distribution, which will then be combined with the velocity operator in the PSO algorithm as follows.
| (11) |
where is the combined solution, is the solution generated by the Mantegna Lévy flight, and is the velocity operator for solution i defined in the original PSO algorithm using Equation (4). Compared to the standard CS algorithm that only uses Mantegna Lévy distribution, the LPSONS algorithm provides both better exploitation and exploration.
3.3. The neighborhood search method
Premature convergence is a major issue with the PSO algorithm and its variants. To avoid this issue and at the same time increase the local search, we use Neighborhood Search (NS) so that even with a high step size, the proposed algorithm can still find most of the good solutions. NS has been adopted in various other algorithms to speed up convergence, for instance, Das et al. proposed an efficient algorithm by using both local and global NS methods based on the DE/target-to-best/1 scheme to boost its convergence [50]. In a similar work, Wang et al. developed the DNSPSO algorithm that utilized both local and global NS methods [51]. Zhou et al. introduced an ABC-based algorithm that used the NS operators to produce a trial solution [52].
The general formula for generating a trial solution is based on the following equation:
| (12) |
where , , and are mutually exclusive random number generators in the range of that satisfy and will change at the start of each generation, is the best solution for the current generation ever found by the algorithm, and and are two randomly chosen solutions that must be different from . The LPSONS algorithm uses the following equation to generate a trial solution using NS:
| (13) |
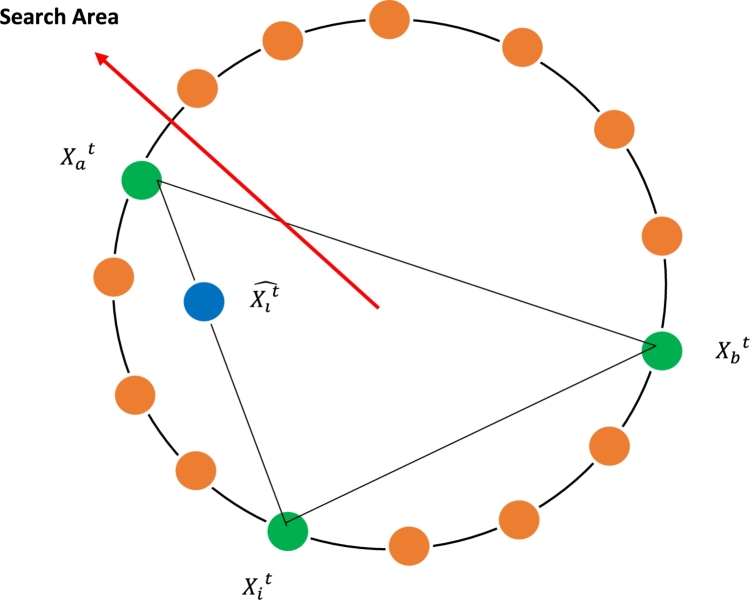
where refers to the current solution in generation t, while are two co-efficients derived from experiments for the purpose of diversifying the solutions in order to generate better ones, is a step size generated by the Mantegna Lévy Distribution which is shown in equation (9), and F is a scaling factor in the range of [0, 1]. Figure 2 depicts the general NS strategy.
Figure 2.
The global NS strategy used in LPSONS.
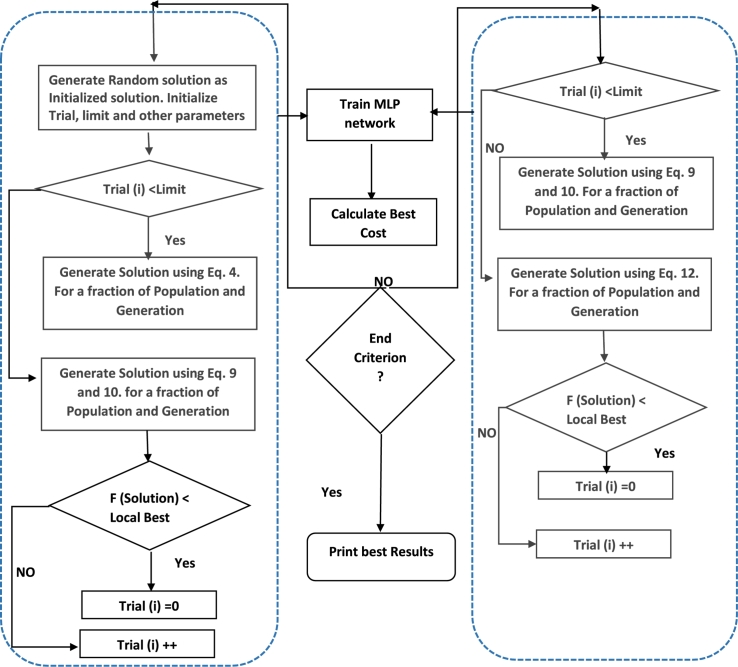
The trial solution will be evaluated against the best solution in terms of fitness value. If it wins the competition, it will survive and be used for the next generation. Figure 3 illustrates the general steps of the LPSONS algorithm.
Figure 3.
The general steps of LPSONS.
Algorithm 2 lists the proposed LPSONS algorithm, which comprises two main phases. The main phases of the proposed algorithm will perform the classification based on the instructions described in Algorithm 3.
Algorithm 2.
LPSONS.
Algorithm 3.
.
The first phase consists of two nested loops. The outer loop runs for a determined generation size set by the user, while the inner loop runs for a determined population size. If the trial set values are less than the limit value, LPSONS will generate new solutions based on the standard PSO algorithm using Equation (4); otherwise, it will use the Mantegna Lévy distribution enhanced PSO algorithm to generate new solutions using Equation (9) and Equation (11). After that, it will compare the fitness value of the generated solution with that of the local best solution to update the trial set accordingly. The second phase also consists of two nested loops with the outer loop for the generation size determined by the user and the inner loop for a determined population size. If the trial set values are less than the limit value, LPSONS will use the Mantegna Lévy distribution enhanced PSO algorithm to generate new solutions using Equation (9) and Equation (11); otherwise, it will further use NS to generate new solutions using Equation (13). After that, the fitness value of the generated solution is compared against that of the local best solution to update the trial set value. Finally, the ever best solution is chosen from those returned in both phases and its fitness value is derived accordingly.
3.4. Encoding strategy
The LPSONS adopts a vector encoding strategy in which particles are represented as randomly generated one-dimensional arrays with values in the range of [-1, 1]. Each generated solution contains connection weights and biases linking the input layer to the hidden layer as well as linking the hidden layer to the output layer. Figure 4 shows a sample solution generated by the proposed algorithm.
Figure 4.
Sample solution generated by LPSONS.
4. Results & discussion
4.1. Datasets
Fourteen standard datasets from the UCI machine learning repository are used to evaluate the LPSONS algorithm in terms of accuracy and efficiency against the benchmark algorithms of LFPSO [23], PSOLF [24], and gradient-based Back Propagation algorithm (BP) [28]. These datasets are Wisconsin breast cancer (denoted as Breast Cancer), Liver, Pima, Wine, Australian, Hepatitis, Heart, Blood, Iris, Credit, Seeds, Haberman, Balance, and Diabetes. Table 1 lists these datasets, including the number of their attributes, classes, and data objects.
Table 1.
Experimental datasets.
| Dataset | Number of Attributes | Number of Classes | Number of data objects |
|---|---|---|---|
| Breast Cancer | 10 | 2 | 683 |
| Liver | 7 | 2 | 345 |
| Pima | 8 | 2 | 768 |
| Wine | 13 | 3 | 178 |
| Australian | 14 | 2 | 690 |
| Hepatitis | 19 | 2 | 155 |
| Heart | 13 | 2 | 297 |
| Blood | 5 | 2 | 748 |
| Iris | 4 | 3 | 150 |
| Credit | 15 | 2 | 690 |
| Seeds | 7 | 3 | 210 |
| Haberman | 3 | 2 | 306 |
| Balance | 4 | 3 | 625 |
| Diabetes (Diabetic Debrecen) | 20 | 2 | 1151 |
4.2. Experiment settings
Every algorithm used in the experiments runs for 30 times with random initial solutions on every dataset. The population size of all algorithms is 100, the number of perceptron in the hidden layer is set to 5, the value of constant variable limit which is indicated in line 2 of Algorithm 2 initialized to 10 for each particle. The datasets are divided into three parts: 70% used for training, 10% used for validation data, and 20% used for testing purpose. For the benchmark purpose, we have implemented the LFPSO and PSOLF algorithms based on their original source codes and utilized BP algorithm according to its standard algorithm. As each algorithm takes a long time to process classification of the given dataset, we have utilized Function Evaluations (FEs = 13000) as the threshold to terminate the process. Table 2 lists all the parameters and their values used by the algorithms. All algorithms have been implemented in Matlab 2016a and executed on a computer with Intel Core i3, 2.5 GHz, 4 GB RAM running Windows 7.
Table 2.
Parameters and Values.
| Algorithm | Parameters | Values |
|---|---|---|
| MLF | β | 1.9 |
| LFPSO | c1, c2, limit | 2, 2, 10 |
| w | ||
| PSOLF | c1, c2, limit | 2, 2, 10 |
| w | ||
| LPSONS | c1, c2, limit | 2, 2, 10 |
| α1, α2, F | 1.49, 1.49, 0.5 | |
| w | ||
4.3. Evaluation measures
We have used Mean Square Error (MSE) as the fitness function for all the training algorithms to be evaluated. The aim of each algorithm is to minimize MSE in order to achieve an optimal network. MSE is defined as follows:
| (14) |
where n is the number of samples, while / are the actual and predicted output respectively.
We have also adopted a confusion matrix as a basis for a number of evaluation metrics used to evaluate the performance of each classifier. In a classification problem, each element I is mapped to a negative label N and a positive label P and accordingly Table 3 lists a confusion matrix for binary classification of instances [28], [53]:
-
•
True Positive (TP): positive instance and positively classified,
-
•
False Negative (FN): positive instance and negatively classified,
-
•
True Negative (TN): negative instance and negatively classified, or
-
•
False Positive (FP): negative instance and positively classified.
Table 3.
Confusion Matrix.
Based on the confusion matrix, the following evaluation metrics are used to measure the performance of each classification algorithm:
-
1.Accuracy: the rate of correctly classified positive and negative instances to all instances.
-
2.Sensitivity (also known as Recall): the rate of classified true positive instances to actual positive instances.
-
3.Specificity: the rate of classified true negative instances to actual negative instances.
-
4.Precision: the rate of classified positive instances to all positive instances that should be classified positive.
-
5.F-Score (also known as F-measure): a harmonic average of Precision and Recall.
4.4. Results and discussions
Table 4, Table 5 show the accuracy measures of the four algorithms for both training and testing respectively involving the 14 datasets. These values are arranged in the order of Best, Mean, and Standard Deviation (Std). Best and Mean respectively indicate the best value and the average value of the accuracy measure for the 30 individual runs, while Std indicates the standard deviation of the achieved values.
Table 4.
Classification Training Accuracy.
| Dataset/Algorithm | BP | PSOLF | LFPSO | LPSONS | |
|---|---|---|---|---|---|
| Breast Cancer | Best | 0.9760 | 0.9790 | 0.9806 | 0.9811 |
| Mean | 0.9721 | 0.9721 | 0.9753 | 0.9759 | |
| Std | 0.0041 | 0.0043 | 0.0046 | 0.0041 | |
| Liver | Best | 0.7837 | 0.7824 | 0.7740 | 0.7866 |
| Mean | 0.7393 | 0.7297 | 0.7535 | 0.7652 | |
| Std | 0.0193 | 0.0248 | 0.0183 | 0.0177 | |
| Pima | Best | 0.7778 | 0.7955 | 0.7744 | 0.7993 |
| Mean | 0.7445 | 0.7825 | 0.7704 | 0.7890 | |
| Std | 0.0137 | 0.0131 | 0.0129 | 0.0076 | |
| Wine | Best | 0.9908 | 1.0000 | 1.0000 | 1.0000 |
| Mean | 0.9872 | 0.9832 | 0.9968 | 1.0000 | |
| Std | 0.0047 | 0.0096 | 0.0056 | 0.0000 | |
| Australian | Best | 0.8929 | 0.8902 | 0.8944 | 0.9586 |
| Mean | 0.8791 | 0.8712 | 0.8819 | 0.8818 | |
| Std | 0.0110 | 0.0090 | 0.0091 | 0.0279 | |
| Hepatitis | Best | 0.9853 | 1.0000 | 1.0000 | 1.0000 |
| Mean | 0.9721 | 0.9619 | 0.9768 | 0.9885 | |
| Std | 0.0162 | 0.0305 | 0.0147 | 0.0128 | |
| Heart | Best | 0.9392 | 0.8956 | 0.9086 | 0.9183 |
| Mean | 0.9116 | 0.8719 | 0.8764 | 0.8894 | |
| Std | 0.0175 | 0.0113 | 0.0170 | 0.0147 | |
| Blood | Best | 0.7934 | 0.7881 | 0.7977 | 0.8015 |
| Mean | 0.7512 | 0.7674 | 0.7807 | 0.7904 | |
| Std | 0.0182 | 0.0134 | 0.0145 | 0.0077 | |
| Iris | Best | 0.9921 | 0.9809 | 0.9904 | 1.0000 |
| Mean | 0.9635 | 0.9519 | 0.9647 | 0.9752 | |
| Std | 0.0323 | 0.0495 | 0.0175 | 0.0163 | |
| Credit | Best | 0.9046 | 0.8905 | 0.8993 | 0.9059 |
| Mean | 0.8825 | 0.8822 | 0.8840 | 0.8877 | |
| Std | 0.0178 | 0.0065 | 0.0084 | 0.0114 | |
| Seeds | Best | 0.9775 | 0.9640 | 0.9640 | 0.9784 |
| Mean | 0.9587 | 0.9489 | 0.9566 | 0.9647 | |
| Std | 0.0123 | 0.0115 | 0.0106 | 0.0110 | |
| Haberman | Best | 0.7810 | 0.7803 | 0.7850 | 0.7803 |
| Mean | 0.7635 | 0.7616 | 0.7612 | 0.7654 | |
| Std | 0.0215 | 0.0136 | 0.0186 | 0.0134 | |
| Balance | Best | 0.8921 | 0.8949 | 0.9640 | 0.8995 |
| Mean | 0.8705 | 0.8741 | 0.8849 | 0.8853 | |
| Std | 0.0189 | 0.0097 | 0.0104 | 0.0090 | |
| Diabetes | Best | 0.7163 | 0.7099 | 0.7229 | 0.7345 |
| Mean | 0.7082 | 0.70.93 | 0.7191 | 0.7109 | |
| Std | 0.0147 | 0.0093 | 0.0084 | 0.0109 | |
Table 5.
Classification Testing Accuracy.
| Dataset/Algorithm | BP | PSOLF | LFPSO | LPSONS | |
|---|---|---|---|---|---|
| Breast Cancer | Best | 0.9748 | 0.9756 | 0.9707 | 0.9756 |
| Mean | 0.9529 | 0.9590 | 0.9590 | 0.9648 | |
| Std | 0.0920 | 0.0116 | 0.0076 | 0.0072 | |
| Liver | Best | 0.8427 | 0.7323 | 0.7058 | 0.7353 |
| Mean | 0.6558 | 0.6469 | 0.6539 | 0.6638 | |
| Std | 0.0495 | 0.0448 | 0.0647 | 0.0450 | |
| Pima | Best | 0.7700 | 0.7823 | 0.7695 | 0.7826 |
| Mean | 0.7235 | 0.7369 | 0.6733 | 0.7426 | |
| Std | 0.0522 | 0.0412 | 0.0751 | 0.0390 | |
| Wine | Best | 0.9259 | 0.9811 | 0.9811 | 1.0000 |
| Mean | 0.8667 | 0.9377 | 0.9413 | 0.9509 | |
| Std | 0.0531 | 0.0427 | 0.0346 | 0.0328 | |
| Australian | Best | 0.8985 | 0.8985 | 0.8888 | 0.8985 |
| Mean | 0.8629 | 0.8604 | 0.8623 | 0.8635 | |
| Std | 0.0325 | 0.0263 | 0.0184 | 0.0223 | |
| Hepatitis | Best | 0.9655 | 0.9117 | 0.8529 | 0.9118 |
| Mean | 0.9211 | 0.7913 | 0.7911 | 0.7941 | |
| Std | 0.0462 | 0.0801 | 0.0426 | 0.0399 | |
| Heart | Best | 0.9870 | 0.8314 | 0.8764 | 0.8539 |
| Mean | 0.8293 | 0.8024 | 0.8258 | 0.8112 | |
| Std | 0.0265 | 0.0183 | 0.0348 | 0.0264 | |
| Blood | Best | 0.8154 | 0.7991 | 0.8214 | 0.8125 |
| Mean | 0.7739 | 0.7713 | 0.7746 | 0.7799 | |
| Std | 0.0425 | 0.0248 | 0.0339 | 0.0244 | |
| Iris | Best | 0.9565 | 0.9777 | 1.0000 | 1.0000 |
| Mean | 0.9230 | 0.9155 | 0.9711 | 0.9755 | |
| Std | 0.0553 | 0.0701 | 0.0298 | 0.0286 | |
| Credit | Best | 0.9529 | 0.8775 | 0.8775 | 0.8826 |
| Mean | 0.9329 | 0.8418 | 0.8250 | 0.8290 | |
| Std | 0.220 | 0.0259 | 0.0587 | 0.0621 | |
| Seeds | Best | 0.9808 | 1.0000 | 0.9833 | 1.0000 |
| Mean | 0.9215 | 0.9416 | 0.9250 | 0.9250 | |
| Std | 0.0393 | 0.0345 | 0.0326 | 0.0479 | |
| Haberman | Best | 0.7872 | 0.7826 | 0.7826 | 0.8043 |
| Mean | 0.7416 | 0.7347 | 0.7360 | 0.7500 | |
| Std | 0.0361 | 0.0370 | 0.0455 | 0.0251 | |
| Balance | Best | 0.8635 | 0.9090 | 0.9037 | 0.9144 |
| Mean | 0.8239 | 0.8883 | 0.8716 | 0.8883 | |
| Std | 0.0424 | 0.0173 | 0.0232 | 0.0200 | |
| Diabetes | Best | 0.6800 | 0.7043 | 0.6795 | 0.7092 |
| Mean | 0.7315 | 0.6392 | 0.6078 | 0.6383 | |
| Std | 0.0369 | 0.0233 | 0.0402 | 0.0221 | |
For the training accuracy, the proposed LPSONS algorithm outperforms LFPSO, PSOLF, and BP for most of the datasets. In terms of Best, LPSONS exhibits superiority for 10/14 datasets: Breast Cancer, Liver, Pima, Australian, Blood, Iris, Credit, Seeds, Balance, and Diabetes, while for Wine and Hepatitis datasets, its performance is exactly the same as those of the benchmark algorithms. In terms of Mean, LPSONS performs better than LFPSO, PSOLF, and BP for 11/14 datasets: Breast Cancer, Liver, Pima, Wine, Hepatitis, Blood, Iris, Credit, Seeds, Haberman, and Balance. LPSONS also displays better Std for 8/14 of the datasets (Breast Cancer, Liver, Pima, Wine, Hepatitis, Blood, Iris, and Haberman), indicating that it is more stable than the benchmark algorithms.
For the testing accuracy, LPSONS also outperforms LFPSO, PSOLF, and BP for most of the datasets. For Best accuracy, it performs better for 7/14 datasets: Pima, Wine, Iris, Credit, Haberman, and Balance and has a similar accuracy for the breast cancer and seeds datasets in comparison to the PSOLF algorithm. For Mean accuracy, it performs better for 8/14 datasets: Breast Cancer, Liver, Pima, Wine, Australian, Blood, Iris, and Haberman. For Std, it shows better stability and robustness for 8/14 datasets: Breast Cancer, Pima, Wine, Hepatitis, Blood, Iris, Haberman, and Diabetes.
Table 6, Table 7 show the mean value of Specificity, Sensitivity, and F-Measure of the four algorithms for both training and testing respectively involving the 14 datasets. The results are organized in the order of Specificity, Sensitivity, and F-measure, all using mean values.
Table 6.
Training Specificity, Sensitivity, and F-Measurere.
| Dataset/Algorithm | BP | PSOLF | LFPSO | LPSONS | |
|---|---|---|---|---|---|
| Breast Cancer | Spec | 0.9495 | 0.9587 | 0.9605 | 0.9615 |
| Sens | 0.9549 | 0.9703 | 0.9735 | 0.9749 | |
| F-Measure | 0.9560 | 0.9696 | 0.9729 | 0.9738 | |
| Liver | Spec | 0.7331 | 0.7309 | 0.7549 | 0.769 |
| Sens | 0.7089 | 0.7029 | 0.7372 | 0.7423 | |
| F-Measure | 0.7327 | 0.7160 | 0.7452 | 0.7526 | |
| Pima | Spec | 0.6633 | 0.7495 | 0.7559 | 0.7506 |
| Sens | 0.6283 | 0.7276 | 0.7373 | 0.7402 | |
| F-Measure | 0.6588 | 0.7495 | 0.7511 | 0.7581 | |
| Wine | Spec | 0.9777 | 0.9904 | 0.9962 | 1.0000 |
| Sens | 0.9713 | 0.9852 | 0.9968 | 0.9980 | |
| F-Measure | 0.9692 | 0.9837 | 0.9967 | 0.9977 | |
| Australian | Spec | 0.8222 | 0.8407 | 0.8598 | 0.8629 |
| Sens | 0.8604 | 0.8719 | 0.8804 | 0.8807 | |
| F-Measure | 0.8691 | 0.8709 | 0.8799 | 0.8805 | |
| Hepatitis | Spec | 0.9275 | 0.9694 | 0.9819 | 0.9892 |
| Sens | 0.7995 | 0.9189 | 0.9465 | 0.9735 | |
| F-Measure | 0.8312 | 0.9322 | 0.9556 | 0.9805 | |
| Heart | Spec | 0.8778 | 0.8926 | 0.8848 | 0.8970 |
| Sens | 0.8655 | 0.8676 | 0.8734 | 0.8870 | |
| F-Measure | 0.8675 | 0.8715 | 0.8755 | 0.8889 | |
| Blood | Spec | 0.6120 | 0.6750 | 0.6726 | 0.6898 |
| Sens | 0.5363 | 0.5625 | 0.5761 | 0.5944 | |
| F-Measure | 0.6205 | 0.6361 | 0.6444 | 0.6609 | |
| Iris | Spec | 0.9762 | 0.9392 | 0.9737 | 0.9854 |
| Sens | 0.9661 | 0.9520 | 0.9665 | 0.9747 | |
| F-Measure | 0.9667 | 0.9528 | 0.9670 | 0.9757 | |
| Credit | Spec | 0.9147 | 0.9177 | 0.9215 | 0.9236 |
| Sens | 0.8850 | 0.8840 | 0.8862 | 0.8561 | |
| F-Measure | 0.8837 | 0.8827 | 0.8848 | 0.8713 | |
| Seeds | Spec | 0.8670 | 0.9605 | 0.9737 | 0.9728 |
| Sens | 0.9360 | 0.9475 | 0.9557 | 0.9641 | |
| F-Measure | 0.9395 | 0.9484 | 0.9567 | 0.9643 | |
| Haberman | Spec | 0.6138 | 0.6296 | 0.6483 | 0.6245 |
| Sens | 0.5717 | 0.5854 | 0.5959 | 0.5845 | |
| F-Measure | 0.6325 | 0.6373 | 0.6491 | 0.6377 | |
| Balance | Spec | 0.7922 | 0.8325 | 0.8884 | 0.9018 |
| Sens | 0.6307 | 0.6372 | 0.6417 | 0.6448 | |
| F-Measure | 0.6769 | 0.6801 | 0.6981 | 0.7013 | |
| Diabetes | Spec | 0.6436 | 0.6925 | 0.6711 | 0.6675 |
| Sens | 0.6835 | 0.7096 | 0.7230 | 0.7137 | |
| F-Measure | 0.6908 | 0.7071 | 0.7217 | 0.7135 | |
Table 7.
Testing Specificity, Sensitivity, and F-Measure.
| Dataset/Algorithm | BP | PSOLF | LFPSO | LPSONS | |
|---|---|---|---|---|---|
| Breast Cancer | Spec | 0.9469 | 0.9410 | 0.9474 | 0.9478 |
| Sens | 0.9549 | 0.9532 | 0.9551 | 0.9617 | |
| F-Measure | 0.9565 | 0.9538 | 0.9556 | 0.9613 | |
| Liver | Spec | 0.7321 | 0.6492 | 0.7090 | 0.6753 |
| Sens | 0.7054 | 0.6104 | 0.6330 | 0.6437 | |
| F-Measure | 0.7987 | 0.6500 | 0.6473 | 0.6704 | |
| Pima | Spec | 0.6632 | 0.6730 | 0.6562 | 0.6803 |
| Sens | 0.6271 | 0.7124 | 0.6209 | 0.7164 | |
| F-Measure | 0.6579 | 0.7104 | 0.6487 | 0.7164 | |
| Wine | Spec | 0.9680 | 0.9689 | 0.9540 | 0.9690 |
| Sens | 0.9549 | 0.9435 | 0.9533 | 0.9580 | |
| F-Measure | 0.9548 | 0.9447 | 0.9541 | 0.9553 | |
| Australian | Spec | 0.8217 | 0.8151 | 0.8186 | 0.8588 |
| Sens | 0.8558 | 0.8647 | 0.8648 | 0.8617 | |
| F-Measure | 0.8589 | 0.8621 | 0.8635 | 0.8632 | |
| Hepatitis | Spec | 0.9254 | 0.8947 | 0.8782 | 0.8961 |
| Sens | 0.7805 | 0.6468 | 0.6418 | 0.6509 | |
| F-Measure | 0.8260 | 0.6425 | 0.6314 | 0.6479 | |
| Heart | Spec | 0.8772 | 0.8097 | 0.8325 | 0.8002 |
| Sens | 0.8629 | 0.8012 | 0.8221 | 0.8093 | |
| F-Measure | 0.8651 | 0.8027 | 0.8221 | 0.8101 | |
| Blood | Spec | 0.6271 | 0.6578 | 0.6359 | 0.6600 |
| Sens | 0.5334 | 0.5627 | 0.5646 | 0.5724 | |
| F-Measure | 0.6319 | 0.6316 | 0.6345 | 0.6400 | |
| Iris | Spec | 0.9635 | 0.9373 | 0.9638 | 0.9684 |
| Sens | 0.9602 | 0.9150 | 0.9543 | 0.9609 | |
| F-Measure | 0.9626 | 0.9195 | 0.9571 | 0.9637 | |
| Credit | Spec | 0.9148 | 0.8805 | 0.8491 | 0.8792 |
| Sens | 0.8844 | 0.8436 | 0.8194 | 0.8310 | |
| F-Measure | 0.8830 | 0.8437 | 0.8310 | 0.8359 | |
| Seeds | Spec | 0.8625 | 0.9395 | 0.9197 | 0.9562 |
| Sens | 0.9227 | 0.9302 | 0.9290 | 0.9274 | |
| F-Measure | 0.9162 | 0.9294 | 0.9263 | 0.9274 | |
| Haberman | Spec | 0.6535 | 0.5933 | 0.5183 | 0.6792 |
| Sens | 0.5654 | 0.5813 | 0.6091 | 0.6142 | |
| F-Measure | 0.6348 | 0.6312 | 0.6298 | 0.6651 | |
| Balance | Spec | 0.7913 | 0.8523 | 0.8781 | 0.8930 |
| Sens | 0.6306 | 0.6366 | 0.6309 | 0.6427 | |
| F-Measure | 0.6511 | 0.6625 | 0.6541 | 0.6961 | |
| Diabetes | Spec | 0.6232 | 0.6482 | 0.6465 | 0.6532 |
| Sens | 0.6031 | 0.6377 | 0.6207 | 0.6347 | |
| F-Measure | 0.6204 | 0.6567 | 0.6244 | 0.6502 | |
For all the three measures on training networks, LPSONS displays better performance than the three benchmark algorithms do. Particularly in terms of Specificity, LPSONS does better for 10/14 datasets: Breast Cancer, Liver, Wine, Australian, Hepatitis, Heart, Blood, Iris, Credit, and Balance. In terms of Sensitivity, it yields better results for 11/14 datasets: Breast Cancer, Liver, Pima, Wine, Australian, Hepatitis, Heart, Blood, Iris, Seeds, and Balance. In terms of F-Measure, it excels for 11/14 datasets: Breast Cancer, Liver, Pima, Wine, Australian, Hepatitis, Heart, Blood, Iris, Seeds, and Balance. LPSONS also performs better in testing ANNs. For example, in terms of Specificity, LPSONS does better for 10/14 datasets: Breast Cancer, Pima, Wine, Australian, Blood, Iris, Seeds, Haberman, Balance, and Diabetes. In terms of Sensitivity, it reveals superiority for 7/14 datasets: Breast Cancer, Pima, Wine, Blood, Iris, Haberman, and Balance. In terms of F-Measure, it produces better results in 7/14 datasets: Breast Cancer, Pima, Australian, Blood, Iris, Haberman, and Balance.
Table 8, Table 9 show the mean MSE and its mean Std of the four algorithms for both training and testing respectively involving the 14 datasets. For training, LPSONS outperforms the benchmark algorithms in 13/14 datasets: Breast Cancer, Liver, Pima, Wine, Australian, Hepatitis, Blood, Iris, Credit, Seeds, Haberman, Balance, and Diabetes in terms of MSE and in 9/14 datasets: Breast Cancer, Pima, Wine, Australian, Hepatitis, Iris, Credit, Seeds, and Balance in terms of Std respectively. For testing, LPSONS outperforms the benchmark algorithms in 10/14 datasets: Breast Cancer (denoted as breast cancer), Pima, Wine, Australian, Blood, Iris, Seeds, Haberman, Balance, and Diabetes in terms of MSE and in 9/14 datasets: Pima, Australian, Hepatitis, Blood, Iris, Seeds, Haberman, Balance, and Diabetes in terms of Std respectively.
Table 8.
Training MSE.
| Dataset/Algorithm | BP | PSOLF | LFPSO | LPSONS | |
|---|---|---|---|---|---|
| Breast Cancer | MSE | 0.0311 | 0.0242 | 0.0417 | 0.0210 |
| Std | 0.0041 | 0.0034 | 0.0635 | 0.0033 | |
| Liver | MSE | 0.1914 | 0.1977 | 0.1889 | 0.1818 |
| Std | 0.0145 | 0.0091 | 0.0047 | 0.0070 | |
| Pima | MSE | 0.1903 | 0.1536 | 0.1711 | 0.1472 |
| Std | 0.0051 | 0.0048 | 0.0171 | 0.0041 | |
| Wine | MSE | 0.0418 | 0.0306 | 0.0200 | 0.0146 |
| Std | 0.0063 | 0.0056 | 0.0048 | 0.0029 | |
| Australian | MSE | 0.1089 | 0.0994 | 0.0949 | 0.0910 |
| Std | 0.0070 | 0.0054 | 0.0054 | 0.0044 | |
| Hepatitis | MSE | 0.0749 | 0.0452 | 0.0314 | 0.0247 |
| Std | 0.0185 | 0.0160 | 0.0094 | 0.0091 | |
| Heart | MSE | 0.1006 | 0.0945 | 0.0995 | 0.1508 |
| Std | 0.0127 | 0.0049 | 0.0075 | 0.0055 | |
| Blood | MSE | 0.1607 | 0.1518 | 0.1527 | 0.1428 |
| Std | 0.0070 | 0.0041 | 0.0037 | 0.0050 | |
| Iris | MSE | 0.0383 | 0.0427 | 0.0281 | 0.0258 |
| Std | 0.0265 | 0.0230 | 0.0048 | 0.0044 | |
| Credit | MSE | 0.0934 | 0.0943 | 0.0916 | 0.0884 |
| Std | 0.0074 | 0.0035 | 0.0044 | 0.0034 | |
| Seeds | MSE | 0.0680 | 0.0408 | 0.0309 | 0.0281 |
| Std | 0.0259 | 0.0061 | 0.0037 | 0.0033 | |
| Haberman | MSE | 0.1777 | 0.1676 | 0.1665 | 0.1654 |
| Std | 0.0106 | 0.0087 | 0.0077 | 0.0063 | |
| Balance | MSE | 0.1449 | 0.0703 | 0.0676 | 0.0534 |
| Std | 0.0253 | 0.0081 | 0.0095 | 0.0054 | |
| Diabetes | MSE | 0.1748 | 0.1556 | 0.1515 | 0.1477 |
| Std | 0.0059 | 0.0027 | 0.0035 | 0.0049 | |
Table 9.
Testing MSE.
| Dataset/Algorithm | BP | PSOLF | LFPSO | LPSONS | |
|---|---|---|---|---|---|
| Breast Cancer | MSE | 0.0310 | 0.0340 | 0.0333 | 0.0299 |
| Std | 0.0079 | 0.0100 | 0.0052 | 0.0067 | |
| Liver | MSE | 0.1928 | 0.2003 | 0.2265 | 0.2577 |
| Std | 0.0201 | 0.0343 | 0.0199 | 0.0329 | |
| Pima | MSE | 0.1907 | 0.1875 | 0.2446 | 0.1863 |
| Std | 0.0101 | 0.0275 | 0.0536 | 0.0267 | |
| Wine | MSE | 0.0417 | 0.0585 | 0.0467 | 0.0396 |
| Std | 0.0313 | 0.0228 | 0.0131 | 0.0146 | |
| Australian | MSE | 0.1087 | 0.1113 | 0.1168 | 0.1087 |
| Std | 0.0141 | 0.0146 | 0.0128 | 0.0125 | |
| Hepatitis | MSE | 0.0784 | 0.1959 | 0.2082 | 0.1927 |
| Std | 0.0879 | 0.0617 | 0.0577 | 0.0506 | |
| Heart | MSE | 0.1024 | 0.1514 | 0.1375 | 0.1570 |
| Std | 0.0217 | 0.0149 | 0.0196 | 0.0207 | |
| Blood | MSE | 0.1606 | 0.1609 | 0.1603 | 0.1579 |
| Std | 0.0229 | 0.0177 | 0.0162 | 0.0159 | |
| Iris | MSE | 0.0399 | 0.0629 | 0.0392 | 0.0363 |
| Std | 0.0152 | 0.0409 | 0.0157 | 0.0129 | |
| Credit | MSE | 0.0938 | 0.1284 | 0.1378 | 0.1587 |
| Std | 0.0346 | 0.0146 | 0.0271 | 0.0540 | |
| Seeds | MSE | 0.0757 | 0.0509 | 0.0511 | 0.0455 |
| Std | 0.0423 | 0.0148 | 0.0126 | 0.0115 | |
| Haberman | MSE | 0.1792 | 0.1901 | 0.1910 | 0.1790 |
| Std | 0.0213 | 0.0182 | 0.0234 | 0.0137 | |
| Balance | MSE | 0.1462 | 0.0660 | 0.0717 | 0.0565 |
| Std | 0.0337 | 0.0090 | 0.0117 | 0.0081 | |
| Diabetes | MSE | 0.1751 | 0.1740 | 0.1806 | 0.1737 |
| Std | 0.0111 | 0.0109 | 0.0198 | 0.0027 | |
In terms of average computational time, all algorithms have been executed for 13,000 function evaluations (FEs) as a fair measure criterion. As shown in Table 10, the BP algorithm takes the longest time, while the LFPSO algorithm is the fastest one. The proposed LPSONS algorithm is the second fastest algorithm, slightly slower than LFPSO but performing significantly better than LFPSO in terms of most evaluation measures.
Table 10.
Average Computational Time (Seconds).
| Datasets | Average Computational Time |
|||
|---|---|---|---|---|
| BP | PSOLF | LFPSO | LPSONS | |
| Breast Cancer | 839.3459 | 281.9295 | 196.0042 | 236.9956 |
| Liver | 413.4199 | 249.6352 | 234.4620 | 246.4468 |
| Pima | 413.0324 | 281.5354 | 210.7203 | 236.5657 |
| Wine | 473.9051 | 301.5204 | 211.9306 | 241.1945 |
| Australian | 414.1895 | 219.8676 | 202.8870 | 244.5231 |
| Hepatitis | 445.3621 | 304.756 | 298.6928 | 302.2047 |
| Heart | 401.0953 | 255.58015 | 223.6950 | 226.888 |
| Blood | 509.6808 | 263.2071 | 219.4589 | 249.3311 |
| Iris | 717.8826 | 261.5717 | 239.9011 | 241.0838 |
| Credit | 373.1287 | 259.7465 | 222.1118 | 249.8160 |
| Seeds | 540.9844 | 261.55765 | 232.1413 | 246.2889 |
| Haberman | 499.205 | 252.1027 | 239.4086 | 255.6158 |
| Balance | 411.0724 | 260.3498 | 218.8188 | 247.0611 |
| Diabetes | 410.0023 | 264.14185 | 255.9756 | 257.2963 |
Figure 5, Figure 6 graphically depict the convergence curves on the best MSE achieved for the three PSO-based algorithms to train the network on the 14 datasets. It is clear that the proposed LPSONS algorithm exhibits a better convergence rate for 11/14 of the datasets: Breast Cancer (A), Pima (C), Wine (D), Australian (E), Hepatitis (F), Blood (H), Iris (I), Seeds (K), Haberman (L), Balance (M), and Diabetes (N).
Figure 5.
Convergence Curves on Mean MSE for LPSONS, LFPSO, and PSOLF on Breast Cancer (A), Liver (B), Pima (C), and Wine (D) Datasets to train MLP Neural Network.
Figure 6.
Convergence Curves on Mean MSE for LPSONS, LFPSO, and PSOLF on Australian (E), Hepatits (F), Heart (G), and Blood (H), Iris (I), and Credit (J), Seeds (K), Haberman (L), Balance (M), and Diabetes (N) Datasets to train MLP Neural Network.
One class of optimization algorithms, such as GA and Differential Evaluation (DE), pertains to evolutionary algorithms that utilize abrupt random changes in generated solutions. Another class, such as PSO and ABC, is related to swarm-intelligence based algorithms. Due to the fact that these algorithms need to move in a search space and there is no abrupt change to leap from one side of the search space to another side, they generally cannot perform better than evolutionary algorithms do in terms of exploration. This class of algorithms is guided by the best solution achieved at each stage and hence its performance benefits from exploitation and a good convergence rate. However, the performance of a generated solution is subject to the initial position; if the best solution is located in a local solution, there is a danger of stagnation into the local minimum. Therefore, keeping a good tradeoff between exploration and exploitation is a key factor that enables LPSONS to be more efficient and more robust than both PSOLF and LFPSO for most of the datasets.
A sensitivity analysis has been done to find out the impact of each component and the effects of Mantegna Lévy flight and the Neighborhood search in the LPSONS algorithm. After conducting the experiments involving different components, it is clear that combining PSO operators with Mantegna Lévy flight has a great impact on the global search and it contributes to the convergence speed too, while the NS strategy contributes to the local search. The original PSO algorithm (PSO) can be trapped into local minimum in some cases, leading to lower accuracy; however, running the algorithm with the MLF strategy (MLF) yields better results, confirming that the algorithm can converge to the global optimum due to searching new areas in the search space and good convergence rate. The MLF tries different step sizes resulting in exploring different areas in the search space and avoiding local minima.
As an example, Figure 7, Figure 8 show the results of some experiments on different components of the algorithm in terms of error rate and convergence speed; however, the conducted experiments have been done on different angles. The results are mean values of error rate in both train and test samples using the Iris dataset as well as of the convergence rate in train samples for thirty independent runs involving PSO (the original PSO algorithm), MLF (the algorithm using only MLF and PSO operators to generate the solutions (Equation (11))), and NS (the algorithm using Neighborhood Search to generate solutions (Equation (13))). It is clear that NS alone does not achieve a good convergence rate as it only contributes to local search in the algorithm, while MLF has the most significant impact on the algorithm's convergence rate. However, using both NS and MLF in the algorithm helps achieve the best results as compared to using them alone. In fact, running the algorithm using only PSO helps shed a light on the fact that the original PSO can be trapped into local minimum, while running the algorithm with both NS and MLF proves the fact that the algorithm is more capable of avoiding local minimum thanks to its good convergence speed as well as suitable global and local search. Thus, due to the good global search, convergence speed, and local search, it can be concluded that MLF and NS can contribute to both good exploration and exploitation. A good exploration prevents from getting into local minima, while a good exploitation suggests efficient convergence speed. Another key point is the division strategy used by the algorithm to help create a good balance between exploration and exploitation, a point that has been proved important in other studies such as [46].
Figure 7.
Error rate of both Train and Test data for original PSO operators (PSO) (a1-a2), Mantegna Lévy Flight (MLF) (b1-b2), and Neighborhood Search (NS) (c1-c2).
Figure 8.
Convergence rate for original PSO operators (PSO), Mantegna Lévy Flight (MLF), and Neighborhood Search (NS).
To statistically test whether there are significant differences between the results produced by LPSONS and those produced by LFPSO, PSOLF, and BP across multiple test attempts, we have conducted Friedman test [54] on the results of training and testing accuracy as well as of training and testing MSE with the significance level of 5%. If the p-value of a test is not greater than 0.05, the null hypothesis is rejected, in other words, the difference is significant. Table 11 lists the statistical test results from which it is clear that the results produced by LPSONS are statistically significant, which confirms that they are deterministic rather than achieved stochastically or by chance.
Table 11.
Friedman test.
| Measures | Statistical Value | P-Value | Null Hypothesis |
|---|---|---|---|
| Training Accuracy | 25.06 | 1.50185e-05 | Rejected |
| Testing Accuracy | 10.25 | 0.0166 | Rejected |
| Training MSE | 26.31 | 8.19622e-06 | Rejected |
| Testing MSE | 9.86 | 0.0198 | Rejected |
5. Conclusions
Motivated by the identified gaps of premature convergence and local optima stagnation in the family of swarm-intelligence based algorithms from the literature and inspired by the NFL theorem, this paper has presented a robust and efficient hybrid approach to optimizing the training of feedforward MLP neural networks by utilizing Mantegna Lévy Flight, PSO operators, and the global neighborhood search strategy. The proposed LPSONS algorithm has been evaluated against two well-known swarm-intelligence based algorithms LFPSO and PSOLF, as well as a gradient-based Back Propagation (BP) algorithm. PSOLF and LFPSO both enhanced the original PSO algorithm using Lévy flight.
With fourteen standard datasets from UCI machine learning repository, LPSONS has significantly outperformed the employed benchmark algorithms in terms of the measurement metrics of Accuracy, Specificity, Recall, and F-measure for the classification of data. Furthermore, it reveals less error rate and better convergence speed in terms of mean MSE. It can be concluded that the proposed approach is a good trainer for MLP neural networks as it can avoid from local minima through a good balance between exploration and exploitation and at the same time is fast and flexible enough to handle a diversity of real-world classification problems.
In future work, we will apply and extend LPSONS to other ANN structures. We will also explore using the proposed approach to solve function approximation problems and other problems such as text clustering and feature subset selection. Furthermore, it is important to investigate how LPSONS works when solving complex classification problems.
Declarations
Author contribution statement
Omid Tarkhaneh: Conceived and designed the experiments; Performed the experiments; Wrote the paper.
Haifeng Shen: Analyzed and interpreted the data; Contributed reagents, materials, analysis tools or data.
Funding statement
This research did not receive any specific grant from funding agencies in the public, commercial, or not-for-profit sectors.
Competing interest statement
The authors declare no conflict of interest.
Additional information
Data associated with this study has been deposited at
https://archive.ics.uci.edu/ml/datasets/Breast+Cancer+Wisconsin+%28Original%29
https://archive.ics.uci.edu/ml/machine-learning-databases/liver-disorders/
https://raw.githubusercontent.com/jbrownlee/Datasets/master/pima-indians-diabetes.data.csv
https://archive.ics.uci.edu/ml/machine-learning-databases/wine/
http://archive.ics.uci.edu/ml/datasets/statlog+(australian+credit+approval)
https://archive.ics.uci.edu/ml/datasets/hepatitis
http://archive.ics.uci.edu/ml/machine-learning-databases/statlog/heart/
https://archive.ics.uci.edu/ml/datasets/Blood+Transfusion+Service+Center
https://archive.ics.uci.edu/ml/datasets/iris
https://archive.ics.uci.edu/ml/datasets/credit+approval
https://archive.ics.uci.edu/ml/datasets/seeds
https://archive.ics.uci.edu/ml/datasets/Haberman's+Survival
http://archive.ics.uci.edu/ml/datasets/balance+scale
https://archive.ics.uci.edu/ml/datasets/Diabetic+Retinopathy+Debrecen+Data+Set
References
- 1.Paliwal M., Kumar U.A. Neural networks and statistical techniques: a review of applications. Expert Syst. Appl. 2009;36(1):2–17. [Google Scholar]
- 2.Uğuz H. A biomedical system based on artificial neural network and principal component analysis for diagnosis of the heart valve diseases. J. Med. Syst. 2010;36(1):61–72. doi: 10.1007/s10916-010-9446-7. [DOI] [PubMed] [Google Scholar]
- 3.Khan J., Wei J.S., Ringnér M., Saal L.H., Ladanyi M., Westermann F., Berthold F., Schwab M., Antonescu C.R., Peterson C., Meltzer P.S. Classification and diagnostic prediction of cancers using gene expression profiling and artificial neural networks. Nat. Med. 2001;7(6):673–679. doi: 10.1038/89044. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Abbass H.A. An evolutionary artificial neural networks approach for breast cancer diagnosis. Artif. Intell. Med. 2002;25(3):265–281. doi: 10.1016/s0933-3657(02)00028-3. [DOI] [PubMed] [Google Scholar]
- 5.Fernandez-Blanco E., Rivero D., Rabuñal J., Dorado J., Pazos A., Munteanu C.R. Automatic seizure detection based on star graph topological indices. J. Neurosci. Methods. 2012;209(2):410–419. doi: 10.1016/j.jneumeth.2012.07.004. [DOI] [PubMed] [Google Scholar]
- 6.Anagnostopoulos I., Maglogiannis I. Neural network-based diagnostic and prognostic estimations in breast cancer microscopic instances. Med. Biol. Eng. Comput. 2006;44(9):773–784. doi: 10.1007/s11517-006-0079-4. [DOI] [PubMed] [Google Scholar]
- 7.Almeida J.S. Predictive non-linear modeling of complex data by artificial neural networks. Curr. Opin. Biotechnol. 2002;13(1):72–76. doi: 10.1016/s0958-1669(02)00288-4. [DOI] [PubMed] [Google Scholar]
- 8.Rummelhart D.E. Parallel Distributed Processing: I. Foundations. 1986. Learning internal representations by error propagation; pp. 318–362. [Google Scholar]
- 9.Schaffer J., Whitley D., Eshelman L. [Proceedings] COGANN-92: International Workshop on Combinations of Genetic Algorithms and Neural Networks. IEEE Comput. Soc. Press; 1992. Combinations of genetic algorithms and neural networks: a survey of the state of the art. [Google Scholar]
- 10.Kennedy J., Eberhart R. Proceedings of ICNN 95 - International Conference on Neural Networks. IEEE; 1995. Particle swarm optimization. [Google Scholar]
- 11.Yu J., Wang S., Xi L. Evolving artificial neural networks using an improved PSO and DPSO. Neurocomputing. 2008;71(4–6):1054–1060. [Google Scholar]
- 12.Zhao N., Wu Z., Zhao Y., Quan T. Ant colony optimization algorithm with mutation mechanism and its applications. Expert Syst. Appl. 2010;37(7):4805–4810. [Google Scholar]
- 13.Karaboga D. Erciyes University, Engineering Faculty, Computer Engineering Department; 2005. An Idea Based on Honey Bee Swarm for Numerical Optimization. Technical report-tr06. [Google Scholar]
- 14.Wang H., Sun H., Li C., Rahnamayan S., shyang Pan J. Diversity enhanced particle swarm optimization with neighborhood search. Inf. Sci. 2013;223:119–135. [Google Scholar]
- 15.Moezi S.A., Zakeri E., Zare A., Nedaei M. On the application of modified cuckoo optimization algorithm to the crack detection problem of cantilever Euler–Bernoulli beam. Comput. Struct. 2015;157:42–50. [Google Scholar]
- 16.Tanabe R., Fukunaga A. 2013 IEEE Congress on Evolutionary Computation. IEEE; 2013. Success-history based parameter adaptation for differential evolution. [Google Scholar]
- 17.Dai X., Yuan X., Zhang Z. A self-adaptive multi-objective harmony search algorithm based on harmony memory variance. Appl. Soft Comput. 2015;35:541–557. [Google Scholar]
- 18.Mallipeddi R., Wu G., Lee M., Suganthan P.N. Gaussian adaptation based parameter adaptation for differential evolution. 2014 IEEE Congress on Evolutionary Computation; CEC; IEEE; 2014. [Google Scholar]
- 19.Melin P., Olivas F., Castillo O., Valdez F., Soria J., Valdez M. Optimal design of fuzzy classification systems using PSO with dynamic parameter adaptation through fuzzy logic. Expert Syst. Appl. 2013;40(8):3196–3206. [Google Scholar]
- 20.Sharma K., Gupta P., Sharma H. Fully informed artificial bee colony algorithm. J. Exp. Theor. Artif. Intell. 2015;28(1–2):403–416. [Google Scholar]
- 21.Tsai H.-C. Novel bees algorithm: stochastic self-adaptive neighborhood. Appl. Math. Comput. 2014;247:1161–1172. [Google Scholar]
- 22.Hu Z., Cai X., Fan Z. An improved memetic algorithm using ring neighborhood topology for constrained optimization. Soft Comput. 2013;18(10):2023–2041. [Google Scholar]
- 23.Haklı H., Uğuz H. A novel particle swarm optimization algorithm with Levy flight. Appl. Soft Comput. 2014;23:333–345. [Google Scholar]
- 24.Jensi R., Jiji G.W. An enhanced particle swarm optimization with Levy flight for global optimization. Appl. Soft Comput. 2016;43:248–261. [Google Scholar]
- 25.Wolpert D., Macready W. No free lunch theorems for optimization. IEEE Trans. Evol. Comput. 1997;1(1):67–82. [Google Scholar]
- 26.Yang X.-S. Experimental Algorithms. Springer; Berlin, Heidelberg: 2011. Metaheuristic optimization: algorithm analysis and open problems; pp. 21–32. [Google Scholar]
- 27.Csáji B.C. Faculty of Sciences, Etvs Lornd University; Hungary: 2001. Approximation with Artificial Neural Networks, vol. 24; p. 48. [Google Scholar]
- 28.Faris H., Aljarah I., Al-Madi N., Mirjalili S. Optimizing the learning process of feedforward neural networks using lightning search algorithm. Int. J. Artif. Intell. Tools. 2016;25(06) [Google Scholar]
- 29.Green R.C., Wang L., Alam M. Training neural networks using central force optimization and particle swarm optimization: insights and comparisons. Expert Syst. Appl. 2012;39(1):555–563. [Google Scholar]
- 30.Bolaji A.L., Ahmad A.A., Shola P.B. Training of neural network for pattern classification using fireworks algorithm. Int. J. Syst. Assur. Eng. Manag. 2016;9(1):208–215. [Google Scholar]
- 31.Karaboga D., Akay B., Ozturk C. Modeling Decisions for Artificial Intelligence. Springer; Berlin, Heidelberg: 2007. Artificial bee colony (ABC) optimization algorithm for training feed-forward neural networks; pp. 318–329. [Google Scholar]
- 32.Aljarah I., Faris H., Mirjalili S. Optimizing connection weights in neural networks using the whale optimization algorithm. Soft Comput. 2016;22(1):1–15. [Google Scholar]
- 33.Sexton R.S., Dorsey R.E., Johnson J.D. Toward global optimization of neural networks: a comparison of the genetic algorithm and backpropagation. Decis. Support Syst. 1998;22(2):171–185. [Google Scholar]
- 34.Karegowda A.G., Manjunath A., Jayaram M. Application of genetic algorithm optimized neural network connection weights for medical diagnosis of Pima Indians diabetes. Int. J. Soft Comput. 2011;2(2):15–23. [Google Scholar]
- 35.Khan K., Sahai A. A comparison of BA, GA, PSO, BP and LM for training feed forward neural networks in e-learning context. Int. J. Intell. Syst. Appl. 2012;4(7):23–29. [Google Scholar]
- 36.Pawełczyk K., Kawulok M., Nalepa J. Proceedings of the Genetic and Evolutionary Computation Conference Companion on - GECCO 18. ACM Press; 2018. Genetically-trained deep neural networks. [Google Scholar]
- 37.Chen J.-F., Do Q., Hsieh H.-N. Training artificial neural networks by a hybrid PSO-CS algorithm. Algorithms. 2015;8(2):292–308. [Google Scholar]
- 38.Mirjalili S., Hashim S.Z.M., Sardroudi H.M. Training feedforward neural networks using hybrid particle swarm optimization and gravitational search algorithm. Appl. Math. Comput. 2012;218(22):11125–11137. [Google Scholar]
- 39.Ozturk C., Karaboga D. Hybrid artificial bee colony algorithm for neural network training. 2011 IEEE Congress of Evolutionary Computation; CEC; IEEE; 2011. [Google Scholar]
- 40.Rumelhart D.E., McClelland J.L. 1986. Parallel Distributed Processing: Explorations in the Microstructure of Cognition. Volume 1. Foundations. [DOI] [PubMed] [Google Scholar]
- 41.Faris H., Hassonah M.A., Al-Zoubi A.M., Mirjalili S., Aljarah I. A multi-verse optimizer approach for feature selection and optimizing SVM parameters based on a robust system architecture. Neural Comput. Appl. 2017;30(8):2355–2369. [Google Scholar]
- 42.Yang X.-S., Deb S. Cuckoo search via Levy flights. 2009 World Congress on Nature & Biologically Inspired Computing; NaBIC; IEEE; 2009. [Google Scholar]
- 43.Yang X.-S. Luniver Press; 2010. Nature-Inspired Metaheuristic Algorithms. [Google Scholar]
- 44.Yang X.-S., Deb S. Engineering optimisation by cuckoo search. Int. J. Math. Model. Numer. Optim. 2010;1(4):330–343. [Google Scholar]
- 45.Zhang Y., Wang L., Wu Q. Modified adaptive cuckoo search (MACS) algorithm and formal description for global optimisation. Int. J. Comput. Appl. Technol. 2012;44(2):73. [Google Scholar]
- 46.Salgotra R., Singh U., Saha S. New cuckoo search algorithms with enhanced exploration and exploitation properties. Expert Syst. Appl. 2018;95:384–420. [Google Scholar]
- 47.Črepinšek M., Liu S.-H., Mernik M. Exploration and exploitation in evolutionary algorithms. ACM Comput. Surv. 2013;45(3):1–33. [Google Scholar]
- 48.Nasa-ngium P., Sunat K., Chiewchanwattana S. Enhancing modified cuckoo search by using Mantegna Levy flights and chaotic sequences. The 2013 10th International Joint Conference on Computer Science and Software Engineering; JCSSE; IEEE; 2013. [Google Scholar]
- 49.Tarkhaneh O., Isazadeh A., Khamnei H.J. A new hybrid strategy for data clustering using cuckoo search based on Mantegna Levy distribution, PSO and k-means. Int. J. Comput. Appl. Technol. 2018;58(2):137. [Google Scholar]
- 50.Das S., Abraham A., Chakraborty U.K., Konar A. Differential evolution using a neighborhood-based mutation operator. IEEE Trans. Evol. Comput. 2009;13(3):526–553. [Google Scholar]
- 51.Wang H., Wang W., Wu Z. Particle swarm optimization with adaptive mutation for multimodal optimization. Appl. Math. Comput. 2013;221:296–305. [Google Scholar]
- 52.Zhou X., Wang H., Wang M., Wan J. Enhancing the modified artificial bee colony algorithm with neighborhood search. Soft Comput. 2015;21(10):2733–2743. [Google Scholar]
- 53.Chatterjee S., Sarkar S., Hore S., Dey N., Ashour A.S., Balas V.E. Particle swarm optimization trained neural network for structural failure prediction of multistoried RC buildings. Neural Comput. Appl. 2016;28(8):2005–2016. [Google Scholar]
- 54.Derrac J., García S., Molina D., Herrera F. A practical tutorial on the use of nonparametric statistical tests as a methodology for comparing evolutionary and swarm intelligence algorithms. Swarm Evol. Comput. 2011;1(1):3–18. [Google Scholar]