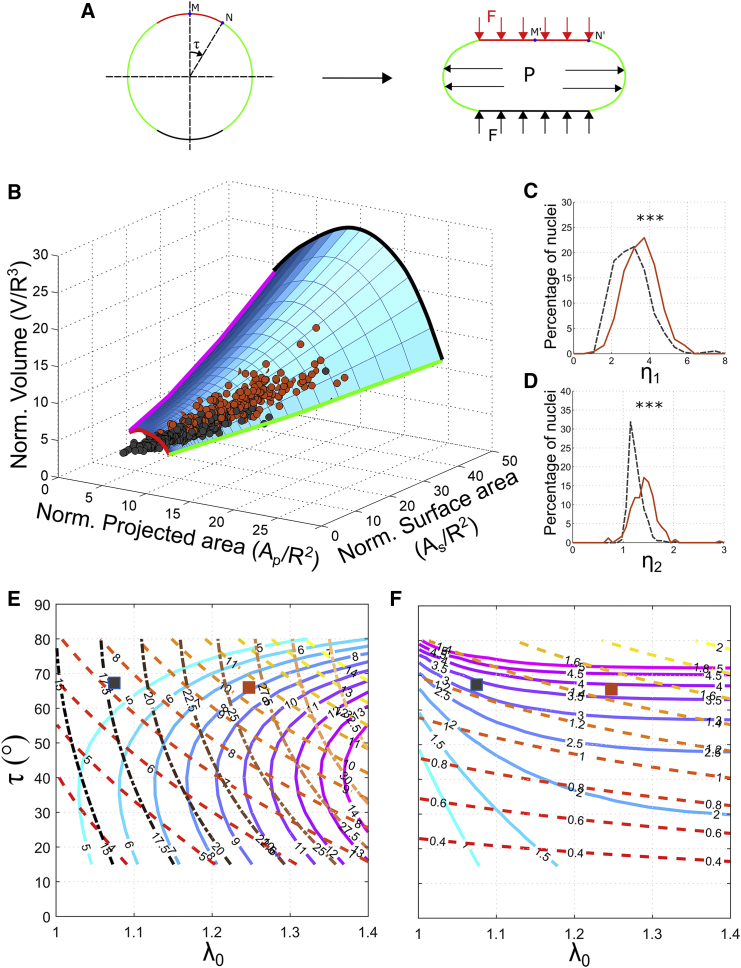
Figure 3.

Nondimensional mechanical model of nuclear morphology. (A) The spherical nuclear envelope is deformed by two forces: 1) an inflating pressure P and 2) a force F due to cortical actin. The force from cortical actin is assumed to be arising from a flat plate that is pushing down on the nucleus. Contact between actin and the nuclear envelope in the deformed state is along the red, horizontal line on the top of the nucleus. The corresponding region in the undeformed configuration is also marked in red. Points N and N′ are the boundary of the contact region in the undeformed and deformed configurations, respectively. The angle subtended by N with the axis of symmetry is the contact angle τ. The stretch at the apex point of the nucleus, M′, is λ₀. (B) Blue surface represents a relationship among the normalized projected area, surface area, and volume of individual nuclei as predicted by the model. Black and red dots are the experimentally measured morphologies of the nuclei of Huh7 and HCV replicon cells, respectively. Almost all individual nuclei lie on the surface predicted by the model. The different boundaries of the surface are marked. Red and black curves are the lower and higher limits, respectively, of the initial stretch λ₀. Magenta and green curves are the lower and higher limits, respectively, of the contact angle τ. Probability distributions of the nondimensional parameters η₁ (C) and η₂ (D) obtained from the experimentally measured nuclear morphologies are shown in Fig. 2. η₁ and η₂ are significantly larger for HCV replicon cells (red, solid lines) in comparison to Huh7 cells (black, dashed lines). ^∗∗∗p < 0.001 by two-tailed Kolmogorov-Smirnov test. (E) Shown are contour curves of normalized volume (solid lines colored blue to magenta), normalized projected area (dashed lines colored red to yellow), and normalized surface area (dash-dot lines colored dark to light brown) as a function of λ₀ and τ. (F) Shown are contour curves of η₁ (solid lines colored blue to magenta) and η₂ (dashed lines colored red to yellow) as a function of λ₀ and τ. By using these contour plots, η₁ and η₂ for any nuclei can be obtained as follows. From the volume, projected area, and surface area of a nucleus, calculate the normalized volume, projected area, and surface area using Eq. 2 by assuming R. From these normalized nuclear shape parameters, obtain λ₀ and τ using the contour plot in (E). η₁ and η₂ can now be obtained from λ₀ and τ using the contour plot in (F). To illustrate the method, we have plotted the mean nuclear morphology of Huh7 (black square) and HCV replicon (red square) cells on (E and F). To see this figure in color, go online.