Abstract
Although genome-wide association studies (GWAS) have successfully identified thousands of genomic loci associated with hundreds of complex traits in the past decade, the debate about such problems as missing heritability and weak interpretability has been appealing for effective computational methods to facilitate the advanced analysis of the vast volume of existing and anticipated genetic data. Towards this goal, gene-level integrative GWAS analysis with the assumption that genes associated with a phenotype tend to be enriched in biological gene sets or gene networks has recently attracted much attention, due to such advantages as straightforward interpretation, less multiple testing burdens, and robustness across studies. However, existing methods in this category usually exploit non-tissue-specific gene networks and thus lack the ability to utilize informative tissue-specific characteristics. To overcome this limitation, we proposed a Bayesian approach called SIGNET (Simultaneously Inference of GeNEs and Tissues) to integrate GWAS data and multiple tissue-specific gene networks for the simultaneous inference of phenotype-associated genes and relevant tissues. Through extensive simulation studies, we showed the effectiveness of our method in finding both associated genes and relevant tissues for a phenotype. In applications to real GWAS data of 14 complex phenotypes, we demonstrated the power of our method in both deciphering genetic basis and discovering biological insights of a phenotype. With this understanding, we expect to see SIGNET as a valuable tool for integrative GWAS analysis, thereby boosting the prevention, diagnosis, and treatment of human inherited diseases and eventually facilitating precision medicine.
Keywords: GWAS, tissue-specific gene networks, Markov random field
Introduction
The identification of causative genetic variation is the primary step towards the understanding of molecular mechanisms of human inherited diseases (Altshuler et al., 2008). Towards this goal, genome-wide association studies (GWAS) have detected thousands of genomic loci that are associated with various complex phenotypes over the past decade, collected in such repository as the GWAS Catalog (Welter et al., 2014). With the rapid development of the high-throughput sequencing technology, it is expected that the number of associated loci will continuously grow as a result of increased sample size, diversity of studied phenotypes, and improved methodology for association discovery (Visscher et al., 2012, 2017). It is no doubt that such fruitful resources could provide unprecedented opportunities for dissecting the genetics of complex diseases, thereby boosting the prevention, diagnosis, and treatment of human diseases and eventually enabling precision medicine (Ashley, 2016). However, at the current stage, both geneticists and bioinformaticians have been suffering from the interpretation of GWAS data, leading to an intense debate about challenges hindering the understanding of the genetic mechanisms underlying complex diseases from these data.
The first challenge is referred to as the missing heritability problem, describing the phenomenon that only limited proportion of the heritability can be explained by those identified significant loci (Manolio et al., 2009). A possible reason for this problem is that many associated loci remain undetected due to the limited sample size and statistical power, and hence the proportion of heritability explained will increase significantly when all markers are considered simultaneously (Yang et al., 2010). The second challenge is that the majority of detected markers locate in noncoding regions, complicating functional interpretation and mechanism understanding as current knowledge on noncoding regions are still very limited (Kellis et al., 2014). The third one is the prevalent existence of correlations between markers, also called linkage disequilibrium (LD), making the precise identification of causal markers challenging (Visscher et al., 2012).
These challenges have been motivating the development of novel approaches to improve the statistical discovery power and infer underlying biological mechanisms by leveraging various functional genomic and epigenomic data, resulting in a series of methods that can be referred to as integrative GWAS analysis (Cantor et al., 2010). Briefly, these methods can be broadly classified into two groups: (i) single nucleotide polymorphism (SNP)-level modeling (Chung et al., 2014; Pickrell, 2014; Li and Kellis, 2016) based on the assumption that SNPs associated with a phenotype tend to be enriched in functionally annotated regions (Maurano et al., 2012) and (ii) gene-level modeling (Pers et al., 2015; Liu et al., 2016) based on the hypothesis that genes associated with a phenotype tend to be enriched in pre-defined gene sets or gene networks (Jiang, 2015; Taşan et al., 2015). Recently, gene-level modeling has attracted much attention due to its advantages over SNP-level modeling, include easier interpretations, less multiple testing burdens, and robustness across studies (Mooney et al., 2014). However, existing gene-level modeling approaches exploit only none tissue-specific gene sets or networks, and recent evidence suggests tissue-specific gene networks provide more specific information about functions of genes (Greene et al., 2015; Marbach et al., 2016), motivating the development of methods for integrating GWAS data with tissue-specific gene networks.
Tissue-specific gene networks, such as co-expression (Pierson et al., 2015), co-functionality (Greene et al., 2015), and regulatory networks (Marbach et al., 2016), have attracted much attention recently. These data provide functional relationships between genes in a tissue-specific manner and show potentials for gene-level integrative GWAS analysis. For example, tissue- or context-specific co-expression networks were shown to be useful for identifying candidate genes of complex diseases (Dobrin et al., 2009; Calabrese et al., 2017) and cancers (He et al., 2012; Zhang et al., 2015). Tissue-specific functional networks were shown to boost power for GWAS gene prioritization (Greene et al., 2015). Tissue-specific regulatory networks were observed to be useful for illustrating phenotype-relevant tissues (Marbach et al., 2016), in which gene regulatory networks of phenotype-relevant tissues were found to be enriched for connections between phenotype-associated genes. Although tissue-specific gene regulatory networks were shown to be useful for revealing phenotype-relevant tissues, their potential for improving gene prioritization remained unexplored (Marbach et al., 2016). Similarly, tissue-specific functional networks were shown to be useful for gene prioritization, but the relevant tissue must be picked by hand (Greene et al., 2015). Intrinsically, gene prioritization and tissue identification are closely related since better gene prioritization would boost tissue identification and vice versa, but thus far these two problems are considered separately in existing methods.
To overcome this limitation, in this paper, we proposed a Bayesian approach named SIGNET for integrating multiple tissue-specific gene networks and GWAS summary data to simultaneously infer phenotype-associated genes and relevant tissues. Specifically, we adopted a Markov random field (MRF) model to incorporate multiple tissue-specific gene networks into integrative GWAS analysis. MRF has been successfully applied to a variety of genomics studies, including gene expression analysis (Lin et al., 2015, 2016), regulatory genomics (Wei and Pan, 2012), and GWAS (Chen et al., 2011). To the best of our knowledge, our method is the first one that utilizes MRF for modeling multiple tissue-specific gene networks in integrative GWAS analysis. By connecting MRF prior of tissue-specific gene networks with GWAS summary data, we created an integrated probabilistic model and utilized Bayesian inference for model estimation. We demonstrated the power of our method through extensive simulation studies regarding both gene prioritization and tissue identification. We then applied our method to 14 real GWAS data of various phenotypes, leading to the discovery of biologically relevant tissues and functional clusters for these phenotypes. Using known association relationships between diseases and genes, we found that our method improved gene prioritization for several complex diseases. Combining the evidence from both simulation studies and real data analysis, we demonstrated that our method would be a valuable tool for post-GWAS analysis. The source code for SIGNET is available at https://github.com/wmmthu/SIGNET.
Results
Schematic diagram of SIGNET
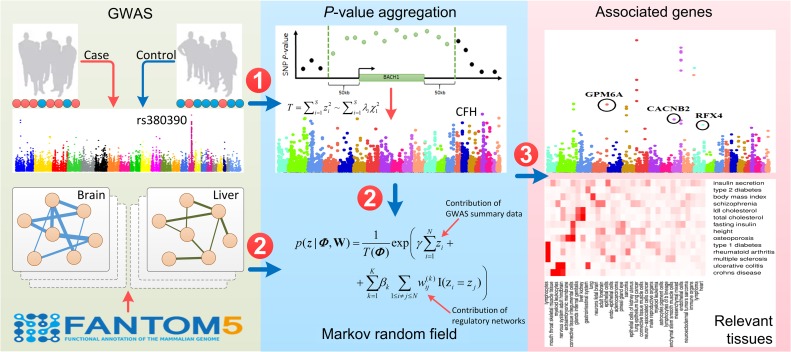
As shown in Figure 1, our method, named SIGNET, takes GWAS summary statistics (i.e. P-values of SNPs) of a particular phenotype and multiple tissue-specific gene networks as input, and produces associated genes and relevant tissues for the phenotype as outputs. To achieve this goal, SIGNET first aggregates P-values of SNPs to obtain P-values of genes, with LD structures along the human genome taken into consideration. The LD structures can be estimated based on a public repository of SNPs such as the 1000 Genomes Project (1000 Genomes Project Consortium, 2012) or an in-house data set with matched population. Then, with the use of a MRF, SIGNET models association status of genes with the phenotype of interest from their P-values, with the incorporation of tissue-specific gene networks for modeling the dependency between the association status of genes. Also, SIGNET uses a spike-and-slab prior to model the distributions of effect sizes of different networks and adopts a Gibbs sampling strategy to infer posterior distributions of gene association status and the inclusion of each gene network, represented as a collection of simulated samples. Finally, SIGNET performs statistical inference for both association status of genes and relevance of gene networks based on these simulated samples, thereby providing a means of gene prioritization and tissue identification. A detailed description of SIGNET is provided in Materials and methods.
Figure 1.
Schematic diagram of SIGNET. Our method takes GWAS summary data and multiple tissue-specific gene networks as input. In the first phase, SNP-level P-values are aggregated into gene-level P-values. In the second phase, a MRF is applied to integrate gene-level P-values and tissue-specific gene networks. In the third phase, an inference procedure gives results for both gene prioritization and tissue identification.
SIGNET is effective in simulation studies
To obtain an intuitive understanding of the parameters involved in SIGNET, we first estimated the parameters , and in our model using real GWAS data of 14 complex phenotypes (Table 1). As shown in Table 2, these parameters showed consistency between different phenotypes. Specifically, parameter controls the shape of the distribution of P-values for genes that are not phenotype-associated. In the ideal case, such gene-level P-values should obey a uniform distribution in the range [0, 1], corresponding to . However, due to the existence of the inflation phenomenon, this parameter typically takes a smaller value. In our case, the estimated values of were in the range [0.566, 1.246] for different phenotypes, and its mean was 0.816. Parameter controls the shape of the distribution of P-values for phenotype-associated genes. Intuitively, phenotype-associated genes should have smaller P-values than those without associations, and thus should be smaller than . In our case, the estimated values of were in the range [0.027, 0.353] for different phenotypes, which was consistent with the above analysis. Parameter controls the probability that a gene is associated with a phenotype without considering the contribution of gene networks. Intuitively, the number of associated genes is typically small, and hence should take negative values. Furthermore, a small means that the probability of association is small, and hence the expected number of associated genes is also small. On the contrary, a large means that the probability of association is large, thereby yielding a large expected number of associated genes. In our case, the estimated values of were in the range [−5.298, −1.279] for different phenotypes, reflecting the diverse numbers of associated genes for different phenotypes, and the estimated values of were correlated with the number of phenotype-associated SNPs (Supplementary Figure S1).
Table 1.
The 14 GWAS datasets.
The first column shows the names of complex traits and the following three columns record the numbers of individuals, cases, and controls in each study. Note that the numbers of cases and controls are only available for complex diseases and not available for complex traits such as height and body mass index. The last three columns represent the number of SNPs genotyped, the number of associations reported in the GWAS Catalog, and corresponding website for downloading data, respectively. NA denotes no available data.
Table 2.
Estimated values of the model parameters for the 14 complex traits.
| Phenotype | |||
|---|---|---|---|
| Multiple sclerosis | 0.939 (0.012) | 0.254 (0.017) | −2.699 (0.140) |
| Ulcerative colitis | 0.566 (0.005) | 0.092 (0.006) | −3.455 (0.101) |
| Crohn’s disease | 0.642 (0.006) | 0.077 (0.005) | −3.394 (0.093) |
| Rheumatoid arthritis | 0.874 (0.008) | 0.044 (0.012) | −5.298 (0.287) |
| Type 1 diabetes | 0.853 (0.007) | 0.066 (0.007) | −4.709 (0.143) |
| LDL cholesterol | 0.767 (0.006) | 0.027 (0.002) | −3.745 (0.065) |
| Total cholesterol | 0.730 (0.007) | 0.033 (0.002) | −3.530 (0.069) |
| Type 2 diabetes | 0.723 (0.009) | 0.123 (0.011) | −3.427 (0.159) |
| Insulin secretion | 0.962 (0.009) | 0.216 (0.077) | −5.127 (0.823) |
| Fasting insulin | 0.781 (0.012) | 0.229 (0.021) | −2.910 (0.237) |
| Schizophrenia | 0.699 (0.014) | 0.351 (0.026) | −1.925 (0.285) |
| Height | 0.948 (0.019) | 0.157 (0.005) | −1.279 (0.058) |
| Body mass index | 1.246 (0.042) | 0.353 (0.020) | −1.433 (0.167) |
| Osteoporosis | 1.026 (0.014) | 0.219 (0.014) | −2.776 (0.127) |
The first column represents phenotype name. The following three columns record parameter estimates of for each phenotype, and each entry represents as mean (standard deviation).
With these understandings, we fixed a set of typical values for these parameters, say, , and , and we conducted the following simulation studies to validate our model. Specifically, we randomly selected tissues from the 32 high-level tissues (Table 3) as phenotype-relevant tissues, and we assigned an equal value of effect size () to the corresponding networks. For the rest tissues, we assigned zero effect sizes. With these parameters, we randomly generated the association status of genes with the phenotype, repeatedly updated the association status using the MRF prior described by the equation (4) for 20 times, and simulated P-values of genes by the conditional distributions specified by the equation (1) (see Materials and methods for details). We then fed the resulting P-values and all the 32 tissue-specific networks into SIGNET to see whether the designated associated genes and relevant tissues could be recovered.
Table 3.
Details about the 32 tissue-specific gene regulatory networks.
| Tissue | #Node | #Edge | Average node degree | Average edge weight |
|---|---|---|---|---|
| Neurons fetal brain | 15104 | 2335943 | 308 | 0.016 |
| Nervous system adult hindbrain | 16005 | 2606819 | 324 | 0.016 |
| Adult forebrain | 16072 | 2662324 | 330 | 0.015 |
| Mesenchymal mixed | 14169 | 1475195 | 208 | 0.014 |
| Sarcoma | 15442 | 2280408 | 294 | 0.014 |
| Endothelial cells | 14240 | 1653967 | 232 | 0.014 |
| Mesenchymal stem smooth muscle cells | 15160 | 2207237 | 290 | 0.015 |
| Connective tissue muscle cells | 15411 | 2373548 | 307 | 0.014 |
| Connective tissue integumental cells | 15525 | 2580570 | 331 | 0.015 |
| lymphocytes | 14089 | 2308803 | 327 | 0.013 |
| Myeloid leukocytes | 15726 | 2833574 | 359 | 0.018 |
| Lymphocytes of b lineage | 14215 | 1987936 | 279 | 0.012 |
| lymphoma | 14168 | 1925674 | 271 | 0.014 |
| Immune organs | 15899 | 2362978 | 296 | 0.013 |
| Myeloid leukemia | 14969 | 2238116 | 298 | 0.014 |
| endo-epithelial cells | 15012 | 1851434 | 246 | 0.014 |
| adenocarcinoma | 14373 | 1542530 | 214 | 0.014 |
| Male reproductive organs | 16494 | 2228707 | 269 | 0.016 |
| Liver & kidney | 16233 | 2302262 | 283 | 0.014 |
| Gastrointestinal system | 15881 | 2059687 | 259 | 0.017 |
| Heart | 15672 | 2252046 | 286 | 0.015 |
| Mouth throat skeletal muscle tissue | 16128 | 2419401 | 299 | 0.016 |
| Lung | 15575 | 1958316 | 251 | 0.014 |
| Glands internal genitalia | 16250 | 2502791 | 307 | 0.015 |
| Pineal gland eye | 15735 | 1779199 | 226 | 0.016 |
| Neuron-associated cells cancer | 16219 | 2654287 | 326 | 0.018 |
| Astrocytes pigment cells | 15355 | 2147224 | 279 | 0.014 |
| Neuroectodermal tumors sarcoma | 15779 | 2563859 | 323 | 0.017 |
| Epithelial cells | 15286 | 2237476 | 292 | 0.014 |
| Extraembryonic membrane | 15407 | 2061130 | 267 | 0.014 |
| Epithelial cells of kidney & uterus | 15279 | 2109521 | 275 | 0.015 |
| Lung epithelium & lung cancer | 15268 | 2274600 | 297 | 0.014 |
The first column denotes the names of tissues, and the following four columns record the number of nodes, the number of edges, average node degrees, and average edge weights, respectively.
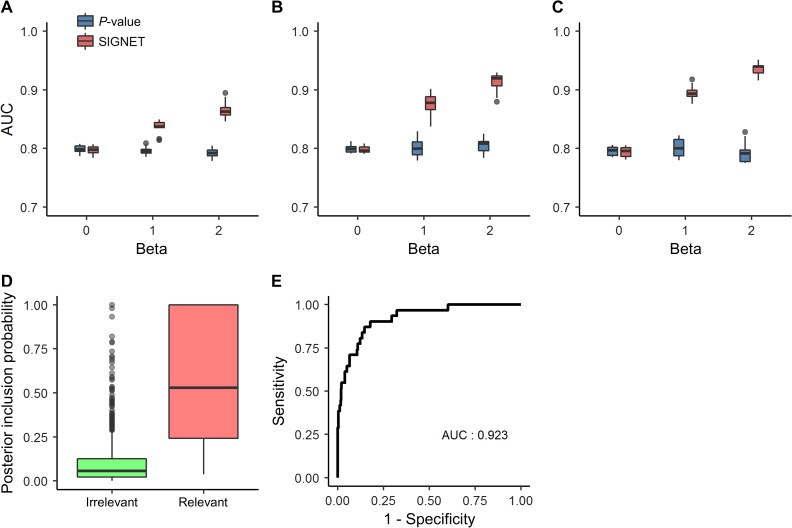
We measured the ability to recover associated genes using a criterion called area under the curve (AUC). Specifically, using the simulated association status as the gold standard, we calculated at a threshold of the local false discovery rate (FDR) (see Materials and methods for details) the sensitivity as the proportion of associated genes whose local FDR below the threshold and the specificity as the proportion of non-associated genes whose local FDR above the threshold. Varying the threshold, we were able to draw a receiver operating characteristic (ROC) curve and calculated the AUC to obtain the AUC value. As mentioned before, there does not exists a method that takes multiple tissue-specific gene networks and GWAS data as inputs thus far, and hence we calculated the AUC using the simulated P-values of genes directly and used this method (P-value for short) as the baseline for comparison. We further repeated the simulation experiment 100 times to eliminate random effects. As shown in Figure 2A, which corresponded to the situation that only one network was designated as relevant (), the performance of our method was almost the same as that of the P-value approach when the relevant network had no effect (). However, when the relevant network had nonzero effect sizes (), our method achieved obvious higher performance than the P-value approach. Furthermore, the performance of our method tended to increase when the effect size of the relevant network increased. We further simulated the situation that multiple networks were included as relevant (), and we observed the similar patterns, as shown in Figure 2B and C.
Figure 2.
Performance of SIGNET on the simulation study. AUCs of SIGNET and P-value for gene prioritization against the effective sizes of relevant tissues, when the numbers of relevant tissues are 1 (A), 2 (B), and 3 (C), respectively. (D) Distributions of PIPs of both irrelevant tissues and relevant tissues. (E) The ROC curve for discriminating relevant tissues from irrelevant ones.
We further investigated the power of our method for identifying phenotype-relevant tissues. To achieve this objective, we introduced a criterion called posterior inclusion probability (PIP, see Materials and methods for details) to measure the likelihood of each tissue being relevant to the phenotype. We plotted distributions of PIPs for designated relevant tissues in the above simulation experiments vs. non-relevant ones in Figure 2D. PIPs for relevant tissues were significantly higher than non-relevant ones, revealing the ability of our method to identify relevant tissues automatically. We further used the simulated relevance status of tissues as the gold standard, calculated sensitivity and specificity at different PIP cut-off values, and plotted the ROC curve in Figure 2E. The curve climbed towards the top-left corner of the plot rapidly (AUC: 0.923), suggesting that relevant tissues could be identified at relatively high accuracy. In addition, we conducted simulation studies for different values of , which exhibited the similar patterns and supported the same conclusion as here (see Supplementary material).
SIGNET reveals tissue specificity of 14 complex traits
To validate the ability of SIGNET to infer relevant tissues for complex traits, we applied our method to 14 complex traits (Table 1) and 32 tissue-specific gene regulatory networks (Table 3) for integrative analysis. Note that these complex traits were analyzed separately. We first explored the relationships between these gene regulatory networks by performing hierarchical clustering. Specifically, for each pair of networks (i.e. and ), we defined the distance between them as
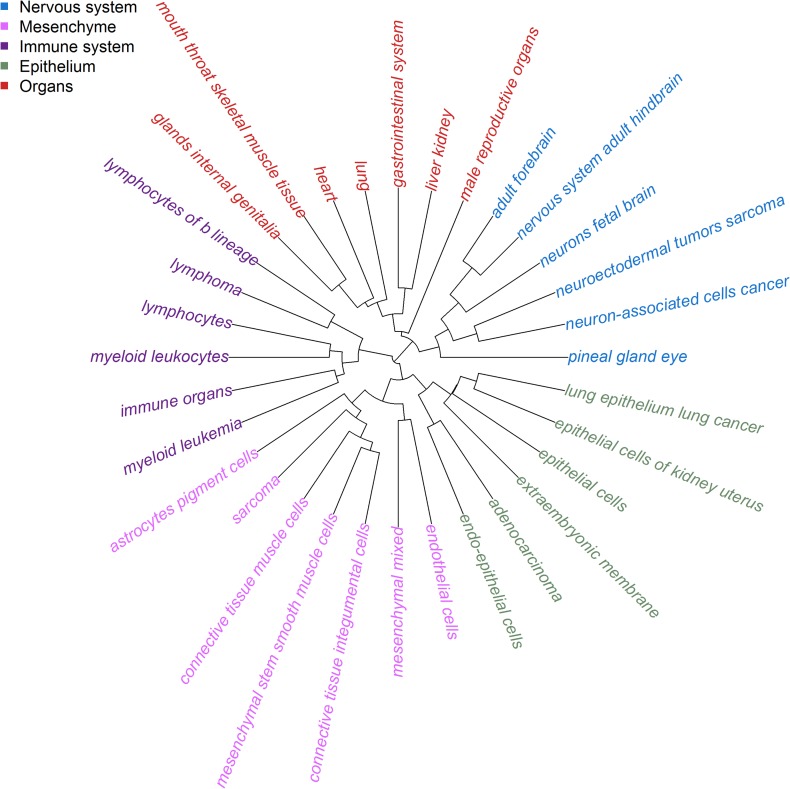
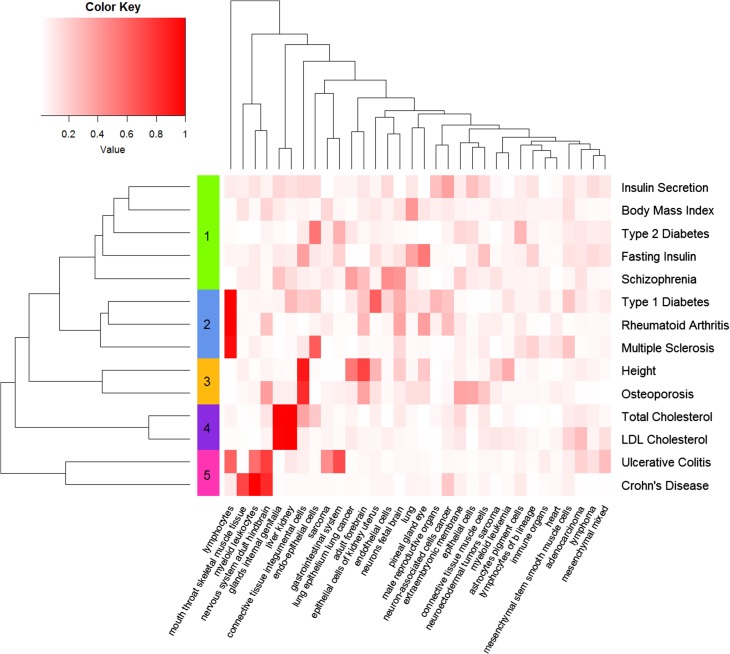
where and were the vectorized adjacency matrices of network and network . Then, hierarchical clustering was performed using the defined distances between each pair of networks, as shown in Figure 3. The gene regulatory networks from similar tissues tended to cluster together. For example, the six tissues from immune system, including lymphocytes of b lineage, lymphoma, lymphocytes, myeloid leukocytes, immune organs, and myeloid leukemia, formed one cluster. Similarly, tissues from nervous system constituted another cluster, and these networks could be grouped into five clusters, including nervous system, mesenchyme, immune system, epithelium, and organs. Next, given the resulting matrix of PIPs regarding the 32 tissue-specific gene regulatory networks and the 14 traits, we conducted a hierarchical cluster analysis on these traits and presented the result in Figure 4, from which we observed several distinct groups of these complex traits.
Figure 3.
Hierarchical clustering of the 32 tissue-specific gene regulatory networks. Hierarchical clustering reveals five clusters, including nervous system, mesenchyme, immune system, epithelium, and organs. Networks from the same cluster are denoted by the same color.
Figure 4.
Cluster analysis of the 14 complex traits by their PIPs across the 32 tissues. Each column denotes a tissue, and each row represents the vector of PIPs across the 32 tissues for a complex trait. The from-white-to-red color represents the value of PIP from low to high. Hierarchical clustering is performed by the vector of PIPs across the 32 tissues, resulting in five clusters.
For example, cluster 1 was composed of five traits, including insulin secretion, body mass index, type 2 diabetes, fasting insulin, and schizophrenia. From the literature, we found that dysfunction of insulin secretion was relevant to type 2 diabetes (Weyer et al., 1999), levels of fasting insulin was associated with diabetes (Johnson et al., 2009), and the body mass index was also related to type 2 diabetes (Tobias et al., 2014). Besides, the association between the body mass index and schizophrenia was reported in a large-scale study (Zammit et al., 2007). As another example, cluster 2 consisted of LDL cholesterol and total cholesterol, and both of the two traits showed obvious relevance to liver and kidney. It is well known that liver is the primary organ responsible for synthesizing cholesterol. Thus it is reasonable to find the association between the two traits and liver. Also, the association between LDL cholesterol and the chronic kidney disease was reported recently (Baigent et al., 2011). As a third example, two traits, height and osteoporosis, were involved in cluster 3. Osteoporosis was believed to be one of the primary reasons for reducing body peak height throughout life (Soranzo et al., 2009), implying the association between osteoporosis and height. In addition, three diseases, type 1 diabetes, rheumatoid arthritis, and multiple sclerosis, were involved in cluster 4. The three diseases were all immune-related, and all of them showed obvious relevance to lymphocytes. From the literature (Sharif et al., 2001; Firestein, 2003; Sospedra and Martin, 2005), we found the evidence supporting associations between lymphocytes, especially T lymphocytes, and the three diseases. Finally, cluster 5 was composed of two diseases, ulcerative colitis and Crohn’s disease. It is well known that the two diseases are two primary types of inflammatory bowel disease (IBD), a group of diseases involving the colon and small intestine. Tissues showing obvious relevance with the two diseases include mouth throat skeletal muscle tissue, myeloid leukocytes, nervous system adult hindbrain, and gastrointestinal system. The association between gastrointestinal system and IBD is evident since both the colon and small intestine are essential components of the gastrointestinal system. It was reported that the level of inflammatory cytokines released by myeloid leukocytes was elevated in IBD patients, and therapeutic depletion of myeloid leukocytes was considered as a non-drug treatment for IBD (Saniabadi et al., 2014). Although the association between IBD and nervous system is still not clear, some neurological symptoms, such as intracerebral focal white-matter lesions revealed by MRI studies, are among the important extra-intestinal manifestations in IBD patients (Ott and Schölmerich, 2013). Additionally, we tried to perform network edge filtering with different thresholds before phenotype cluster analysis (Supplementary Figures S6−S9) and found that the original networks without filtering produced the most reasonable results as described above. These results collectively demonstrated SIGNET as a useful tool for uncovering phenotype-relevant tissues and revealing relationships between different phenotypes.
SIGNET improves gene prioritization performance for six complex diseases
Among the 14 complex traits, we identified six complex diseases, i.e. rheumatoid arthritis, Crohn’s disease, schizophrenia, osteoporosis, multiple sclerosis, and ulcerative colitis, which had at least 10 annotated disease genes in the DisGeNET database (Piñero et al., 2017). In version 4.0 (released in April, 2016), this database contained 429036 disease–gene associations between 17381 genes and >15000 diseases or phenotypes based on the integration of multiple data sources, including OMIM (Hamosh et al., 2005), ClinVar (Landrum et al., 2016), and many others (Rath et al., 2012; Welter et al., 2014). Furthermore, each disease–gene association was assigned a confidence score, which was calculated based on the recurrence of the association across the data sources and their reliabilities, and a larger confidence score indicated a higher probability of the association being real. Since the DisGeNET database did not use any regulatory networks that were used in SIGNET, the disease–gene associations in this database could unbiasedly measure the performance of our method in uncovering disease genes.
For each disease, we varied the threshold for the association confidence score from 0.0 to 0.4 with step size of 0.1, because the numbers of genes with confidence score exceeding than 0.5 were too small (i.e. only one for three diseases and zero for the other diseases). At each threshold of the association confidence score, we labeled genes with confidence scores greater than the threshold as positives and treated the rest genes of whole genome as negatives. Using the labeled genes as the gold standard, we varied the threshold of gene-level local FDRs given by SIGNET, drew the ROC curve, and calculated the corresponding AUC, which measured the performance of a method in uncovering disease genes.
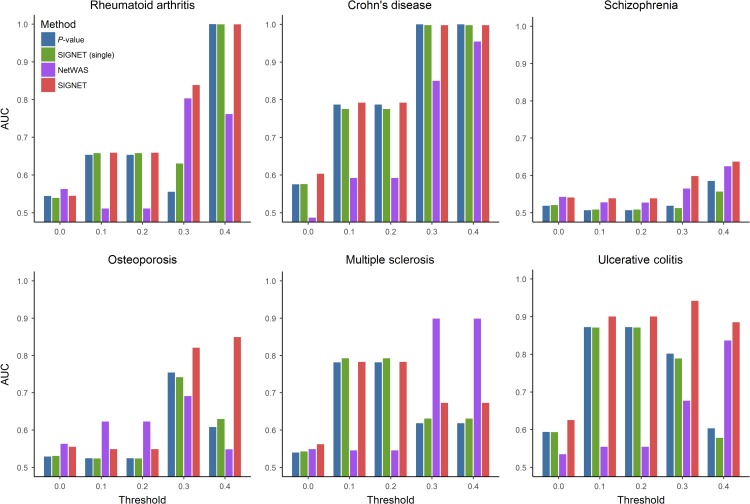
We compared the performance of SIGNET with three baseline approaches: (i) gene-level P-values without consideration of any network information (P-value for short), (ii) SIGNET with a single non-tissue-specific regulatory network (Gerstein et al., 2012) (SIGNET (single) for short), and (iii) NetWAS (Greene et al., 2015). As shown in Figure 5, it was not surprising to see that the performance of all the three methods increased with the increase of the threshold for the association confidence score, because the quality of disease–gene associations tended to be higher at a larger value of the threshold. Furthermore, it was interesting to see that SIGNET showed obviously better or comparable discriminative power than both P-value and SIGNET (single), indicating the effectiveness of our method in uncovering disease genes. As an example, for osteoporosis, SIGNET achieved an AUC of ~0.85 at the threshold of 0.4, while P-value, SIGNET (single), and NetWAS only produced 0.60, 0.62, and 0.55, respectively. Also, we found that the performance of SIGNET (single) was close to that of P-value, implying that the single non-tissue-specific network contained limited information regarding the relationships between transcription factors and disease genes. We drew the similar conclusion that SIGNET performed the best from the performance comparison between these methods in terms of the number of phenotype-associated genes ranked in top k (ranging from 100 to 1000) positions (Supplementary Tables S1−S6). Additionally, we tried to perform network edge filtering with different thresholds before running SIGNET (Supplementary Figure S10) and found that the original networks without filtering leaded to the best performance.
Figure 5.
SIGNET improved gene prioritization for six complex diseases. For each one of the six complex diseases, including rheumatoid arthritis, Crohn’s disease, schizophrenia, osteoporosis, multiple sclerosis, and ulcerative colitis, we extracted corresponding disease genes with evidence scores from the DisGeNET database. The AUCs of SIGNET, SIGNET (single), and P-value are computed under different thresholds for the evidence score. In each subplot, the x-axis denotes the threshold of the evidence score and the y-axis indicates AUC.
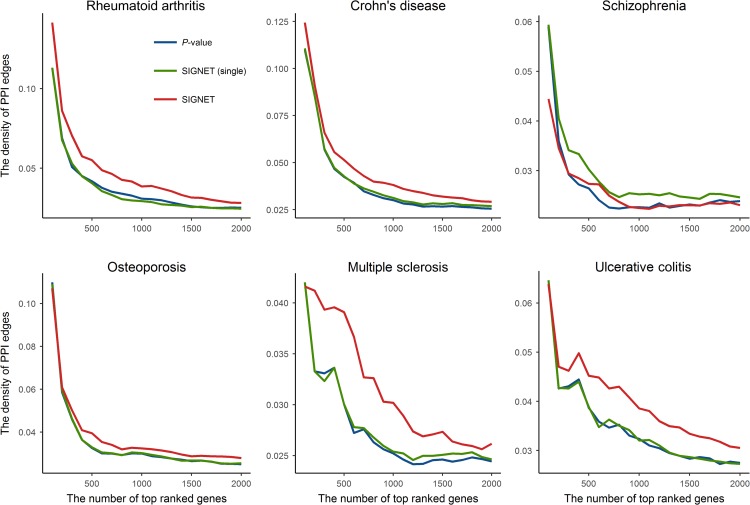
Besides, we tested the hypothesis that disease-associated genes tended to be functionally related, which was previously explored for interpreting GWAS (Pers et al., 2015). We used the protein–protein interaction (PPI) network as a surrogate for measuring functional relatedness between genes because PPI proved to be effective for predicting protein function (Sharan et al., 2007). Specifically, we defined the density of PPI edges among a set of genes as , where is the number of observed PPI edges among these genes. We used the PPI network of human from the STRING database version 10.5 (Szklarczyk et al., 2017) for subsequent analysis. For each of the six diseases examined above, we calculated the density of PPI edges among top genes ranked by P-value, SIGNET (single), and SIGNET, respectively. As shown in Figure 6, the density of PPI edges decreased as we included more genes, which demonstrated that significant genes or top ranked genes tended to connect with each other more densely in the PPI network. Especially, with the same number of top ranked genes, SIGNET leaded to higher density of PPI edges than the other two methods for all diseases except schizophrenia. Therefore, genes prioritized by SIGNET were more likely to be functionally related. We provided the full prioritized gene lists for all of the 14 complex traits in Supplementary Table S1.
Figure 6.
SIGNET improves PPI density among top ranked genes. For each one of the six complex diseases, including rheumatoid arthritis, Crohn’s disease, schizophrenia, osteoporosis, multiple sclerosis, and ulcerative colitis, we calculated the density of PPI edges for top ranked N genes (from 100 to 2000, step size 100). In each subplot, x-axis and y-axis denote the number of top ranked genes and the density of PPI edges, respectively. Note that the results for P-value and SIGNET (single) are similar for some diseases and corresponding lines are also similar, especially in osteoporosis.
These results demonstrated that the incorporation of tissue-specific gene regulatory networks could improve gene prioritization for various complex diseases and the tissue-specific gene regulatory networks were more informative than single gene regulatory network that did not consider tissue-specific information. Therefore, we conjecture that SIGNET, which incorporates tissue-specific gene networks into the analysis of GWAS data, is more powerful than methods without considering tissue-specific relationships between genes in uncovering disease genes and could be a valuable tool for post-GWAS analysis.
Application of SIGNET to Schizophrenia
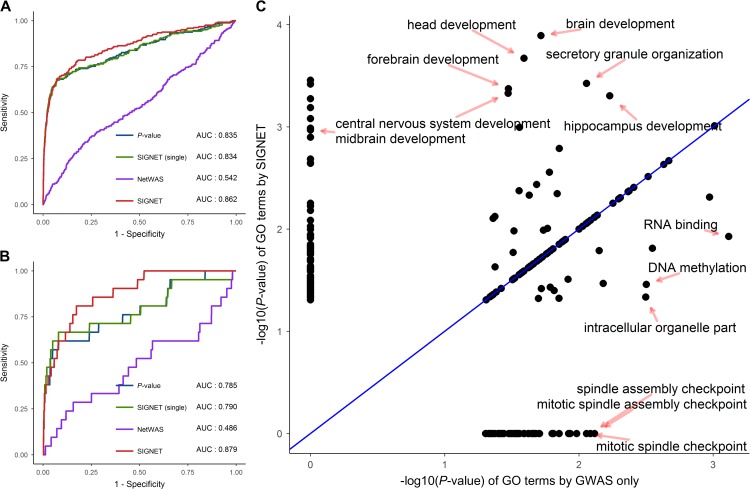
SCZ is a psychiatric disease, characterized by abnormal social behavior and cognitive dysfunction (Ripke et al., 2013). SCZ affects ~1.1% of the population over the age of 18 and is very costly for medical treatment (Saha et al., 2007). A genome-wide association study regarding 9871789 SNPs was previously performed on a cohort consisting of 5001 cases and 6243 controls (Ripke et al., 2013), discovering 13 novel risk loci for SCZ. When applying SIGNET to the summary data of this study and the 32 tissue-specific gene regulatory networks, we estimated that (Table 2), which indicated the existence of inflation in the summary statistics and was consistent with the QQ plot of P-values (Supplementary Figure S4). Among the 32 high-level tissues, two brain-related ones, neurons fetal brain (PIP: 0.548) and adult forebrain (PIP: 0.531), were assigned the highest PIPs, indicating the importance of brain functions for SCZ. At the global FDR cut-off value 0.05, our method detected 25 significant genes, while P-values derived from GWAS data only identified 22 genes, reflecting that SIGNET might be more powerful in finding genes associated with this disease. Within these top ranked genes, it is interesting to see that CACNB2, a gene ranked 107th by P-value and 21st by SIGNET, was recently reported to be associated with SCZ (Juraeva et al., 2014), suggesting the ability of our method in identifying novel disease-associated genes.
Previously, we showed the effectiveness of SIGNET in uncovering disease genes for six diseases with SCZ included based on the DisGeNET database. Here, we validated the performance of SIGNET in prioritizing SCZ-associated genes based on the SZDB database (Wu et al., 2017), a specialized database for SCZ by integrating such data sources as association studies, linkage analysis, copy number analysis, and convergent functional genomics to provide comprehensive biological knowledge about genetics underlying SCZ. Briefly, SZDB contains 2706 candidate genes for SCZ and assigns a polyevidence score (ranges from 1 to 4) to each gene based on the occurrence of evidence from the multiple data sources used. Genes with polyevidence scores 2 were considered as potentially associated with the phenotype. Taking intersection between the SZDB database and the GWAS data, we retrieved 242 genes with a polyevidence score of 2, 21 genes with a polyevidence score of 3, and one gene with a polyevidence score of 4. We then compared the performance of P-value, SIGNET (single) and SIGNET by using the 264 genes with polyevidence score 2 and the 22 genes with polyevidence score 3 as ground truth, respectively. As shown in Figure 7A and B, SIGNET achieved higher AUC than the other two methods, again supporting the effectiveness of SIGNET in the identification of disease genes.
Figure 7.
SIGNET improves gene prioritization and functional analysis for schizophrenia. Using prioritized genes for schizophrenia from the SZDB database as ground truth, we drew the ROC curves of SIGNET (red), SIGNET (single) (green), NetWAS (purple), and P-value (blue) for gene prioritization with the threshold of polyevidence score equal to 2 (A) and 3 (B). (C) Using the top 101 genes (global FDR 0.2) ranked by P-value (or GWAS only) and SIGNET, we conducted GO enrichment analysis and compared the significance of each GO term given by the two methods. Each point represents a GO term, and x-axis and y-axis denote the obtained by GWAS only and SIGNET, respectively.
We further conducted functional analysis by identifying gene ontology (GO) terms enriched among top ranked genes. To achieve this goal, we identified 101 genes whose global FDRs given by SIGNET were smaller than or equal to 0.2, and we detected 52 GO terms that were significantly enriched (P-value < 0.01) among these genes by the ConsensusPathDB (Kamburov et al., 2011). Meanwhile, we ranked genes by P-values derived from the GWAS data in non-decreasing order, identified 101 top ranked genes, and detected 30 GO terms enriched among these genes. We then compared statistical significance (P-values) of GO terms that were identified by the two methods and presented the result in Figure 7C. SIGNET improved significance of several GO terms, including brain development, forebrain development, central nervous system development, hippocampus development, midbrain development, and many others. Interestingly, these terms were apparently related to the functions of the brain. Based on the observation that SIGNET helped to identify SCZ-associated genes, it was natural to think that the functions implicated by these GO terms raised by SIGNET may also be associated with SCZ. For example, the association between brain development and SCZ had been discovered for several decades (Weinberger, 1987), and structural abnormalities in the brain had been observed in SCZ (Pantelis et al., 2005). As another example, a significant decrease of hippocampal volume was observed in SCZ (Heckers and Konradi, 2002), suggesting the association between hippocampus development and SCZ. On the contrary, SIGNET reduced the significance of several GO terms, such as RNA binding, DNA methylation, intracellular organelle part and may others, and these GO terms had less functional implications associated with SCZ than those GO terms enhanced by SIGNET.
In summary, these results collectively demonstrated the effectiveness of SIGNET in discovering SCZ-relevant tissues, prioritizing SCZ-associated genes, and uncovering SCZ-associated GO terms, thereby validating the usefulness of our method in the study of neurological disorders.
Application of SIGNET to ulcerative colitis
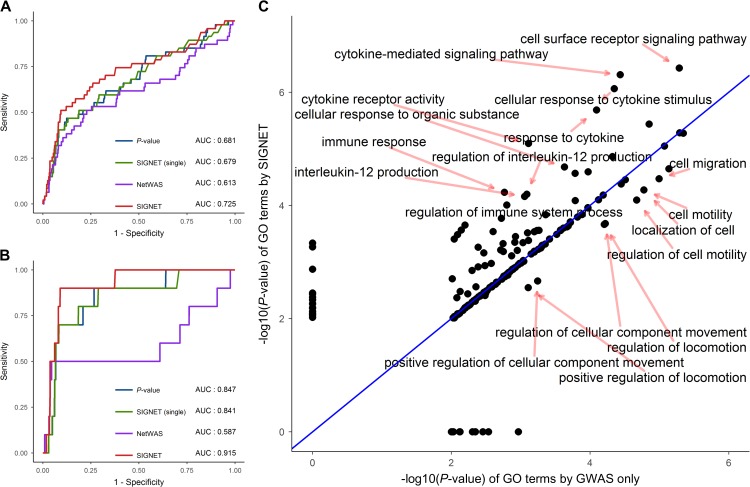
Ulcerative colitis (UC) is a type of IBD, characterized by inflammation and ulcers of several components of the intestine system such as the colon and rectum, and the prevalence of this disease is 7.6–246.0 cases per 100000 per year (Danese and Fiocchi, 2011). An existing genome-wide association study (Anderson et al., 2011) was performed on a cohort consisting of 6687 cases and 19718 controls, and 1428749 SNPs were selected as tested markers, identifying 29 additional risk loci for UC. When applying SIGNET to the summary data of this study and the 32 tissue-specific gene regulatory networks, we estimated that (Table 2), which indicated the existence of inflation in the summary statistics and was consistent with the QQ plot of P-values (Supplementary Figure S4). Among the 32 high-level tissues, three were assigned PIPs above 0.2, including nervous system adult hindbrain (PIP: 1), myeloid leukocytes (PIP: 1), and gastrointestinal system (PIP: 0.795). As explained before, the association between the nervous system and UC may be attributed to the observation that UC is frequently accompanied by disorders of the nervous system (Scheid and Teich, 2007). The myeloid leukocyte is one critical component of the immune system, and its involvement in UC has been reported (Saniabadi et al., 2014). The association between gastrointestinal system and UC is reasonable since UC is a disease with disruption in the gastrointestinal system (Danese and Fiocchi, 2011). With global FDR less than 0.05, our method detected 166 significant genes, compared with 160 significant genes by P-values only. Interestingly, the gene ETS2 was ranked 1249th by P-value and 194th by SIGNET, and it had been reported that genes with ETS2 binding sites were upregulated in UC patients (van der Pouw Kraan et al., 2009), implying the potential association between this gene and UC.
Previously, we showed the effectiveness of SIGNET in uncovering disease genes for six diseases with UC included based on the DisGeNET database. Here, we validated the performance of SIGNET in prioritizing UC-associated genes based on the latest UC GWAS data (Liu et al., 2015; de Lange et al., 2017), containing 63 novel candidate genes for IBD and 13 novel candidate genes for UC. Using the two set of genes as ground truth, we drew the ROC curves of SIGNET, SIGNET (single), and P-value in Figure 8A and B, from which we observed that SIGNET achieved better discriminative performance than the other two methods on these novel genes. For example, using the 13 novel UC-associated candidate genes as ground truth, SIGNET achieved AUC 0.916 compared with 0.847 of P-value and 0.841 of SIGNET (single), as shown in Figure 8B.
Figure 8.
SIGNET improves gene prioritization and functional analysis for ulcerative colitis. Using annotated genes from latest genetic studies for IBD (A) and UC (B), we drew the ROC curves of SIGNET (red), SIGNET (single) (green), NetWAS (purple), and P-value (blue) for gene prioritization. (C) Using the top 166 genes (global FDR 0.05) ranked by P-value (or GWAS only) and SIGNET, we conducted GO enrichment analysis and compared the significance of each GO term given by the two methods. Each point represents a GO term, and x-axis and y-axis denote the obtained by GWAS only and SIGNET, respectively.
We then used the ConsensusPathDB (Kamburov et al., 2011) to conduct functional analysis by finding significant enriched GO terms among the top ranked genes given by P-value and SIGNET, respectively. At the threshold value of 0.05 (global FDR), our method discovered 166 significant genes, and 198 GO terms were enriched (P-value < 0.01) among these genes. Extracting the same number of genes from the rank list produced by P-values derived from the GWAS data, we detected 194 enriched GO terms. We then compared statistical significance (P-values) of GO terms that were identified by the two methods and presented the result in Figure 8C. SIGNET improved significance of several GO terms, including immune response, regulation of immune system process, cytokine-mediated signaling pathways, regulation of interleukin-12 production, and many others. Interestingly, these GO terms indicated apparent associations with the immune system. For example, the crucial role of cytokines in the pathogenesis of UC and IBD has been recognized (Neurath, 2014). As another example, interleukin-12 was observed to be upregulated in IBD (Nielsen et al., 2003), suggesting the association between interleukin-12 and IBD. On the contrary, SIGNET reduced the significance of several GO terms, such as cell migration, localization of cell, and regulation of locomotion, and these GO terms had less functional implications associated with UC than those enhanced by SIGNET.
In summary, these results collectively demonstrated the effectiveness of SIGNET in discovering UC-relevant tissues, prioritizing UC-associated genes, and uncovering UC-associated GO terms, thereby promoting the usefulness of our method in the study of immune diseases.
Discussion
In this paper, we proposed a MRF model called SIGNET to integrate GWAS summary data with multiple tissue-specific gene regulatory networks for the simultaneous inference of phenotype-associated genes and relevant tissues. Through comprehensive simulation studies, we showed the validity of this method in the incorporation of tissue-specific information into traditional association studies. From real data analysis, we demonstrated that main advantages of our method include (i) effective adjustment of gene-level P-values derived from a GWAS data for a particular phenotype, which leaded to high-quality candidate genes that were potentially associated with the phenotype and (ii) quantitative measure of the strength of association between a tissue and a phenotype via a statistic called the posterior inclusion probability, which enabled the identification of relevant tissues for the phenotype. With these hall marks, our method provided a means of utilizing the large volume of available functional genomic data to interpret the vast volume of existing and anticipated genetic data, thereby boosting the power of discovering the underlying mechanism behind human inherited diseases.
Certainly, our method can further be extended from the following aspects. First, besides transcription factors, there are still quite a few regulatory elements involved in gene regulation. How to incorporate such elements as non-coding RNAs (Zhang et al., 2014) and enhancers (Spitz and Furlong, 2012) into a tissue-specific regulatory network is an immediate extension of our current model. Second, different types of genomic and epigenomic data may provide complementary information in describing functional relationships between regulatory elements and genes. Of particular interest is the abundant epigenomic data regarding chromatin accessibility collected in the ENCODE project, with examples including ChIP-seq, DNase-seq, ATAC-seq, and many others. How to utilize such fruitful lines of evidence to construct more reliable tissue-specific networks is another important research topic worth noting. A recent work (Duren et al., 2017) used paired DNase-seq and RNA-seq data to construct tissue-specific gene networks for mouse, and adapting its method to build tissue-specific gene networks for human would be interesting and promising. Third, due to the existence of pleiotropy (Visscher and Yang, 2016), a phenomenon that different phenotypes may share the same underlying causalities, simultaneously modeling of multiple genetically related diseases may further enhance the power of our method. Finally, current GWAS analysis focus on genomic variants, and how to incorporate protein variants (Su et al., 2014) would be interesting.
Materials and methods
Data sources
We collected summary statistics (SNP P-values) of 14 GWAS datasets, including multiple sclerosis (International Multiple Sclerosis Genetics Consortium, and Wellcome Trust Case Control Consortium 2, 2011), ulcerative colitis (Anderson et al., 2011), Crohn’s disease (Franke et al., 2010), rheumatoid arthritis (Stahl et al., 2010), type 1 diabetes (Barrett et al., 2009), LDL cholesterol (Teslovich et al., 2010), total cholesterol (Teslovich et al., 2010), type 2 diabetes (Morris et al., 2012), insulin secretion (Prokopenko et al., 2014), fasting insulin (Scott et al., 2012), schizophrenia (Ripke et al., 2013), height (Allen et al., 2010), BMI (Speliotes et al., 2010), and osteoporosis (Estrada et al., 2012). The details of these GWAS data, including cohort size, the numbers of cases and controls, the number of genotyped SNPs, and corresponding websites, are provided in Table 1. To eliminate bias in our model, we removed genes falling into human leukocyte antigen (HLA) region because of the complex LD structure and clustered association signal in this region.
We collected 32 tissue-specific gene regulatory networks (Marbach et al., 2016), which were derived from the FANTOM5 project data (Andersson et al., 2014). Briefly, Marbach et al. (2016) first mapped peaks identified from Cap Analysis of Gene Expression (CAGE) experiments to promoters and enhancers, and identified their activities across 808 samples, which covered 432 primary cells, 135 tissues, and 241 cell lines. Then, they linked transcription factors (TFs) to promoters and enhancers based on the occurrence of corresponding motifs and evolutionary conservation. Next, they linked promoters to isoforms of genes based on the distance between promoters and transcription start sites (TSSs) of the isoforms. Finally, they connected enhancers to isoforms of target genes based on genomic distance and activity level. They constructed the corresponding regulatory circuit for each sample by using the four types of entities (TF, enhancer, promoter, and gene isoform) as nodes and the derived weighted links between these entities as edges, leading to 808 regulatory circuits. They obtained 394 cell type- and tissue-specific regulatory circuits by merging regulatory circuits of closely related samples. From each tissue-specific regulatory circuit, they defined a TF-gene network by merging edges of TF-promoter and promoter-isoform. These 394 TF-gene networks were further clustered into 32 clusters by hierarchical clustering on pairwise similarities of them, and the similarity between two networks was computed by an extension of the Jaccard index (Marbach et al., 2016). They defined a high-level tissue for each cluster and derived a high-level regulatory network by taking the union of the individual TF-gene networks belonging to the cluster and keeping the maximum edge weights. As shown in the literature (Marbach et al., 2016), the 32 tissue-specific regulatory networks showed stronger enriched signals for GWAS genes compared to individual networks. Thus we selected these 32 tissue-specific regulatory networks for subsequent analysis. Due to pervasive LD structure, association status of two genes to a phenotype may also be highly correlated if they locate physically near to each other. We therefore also removed edges between genes nearby (i.e. located within 1 Mb to each other). Summary statistics of the final networks are shown in Table 3. The histograms of edge weights across these gene networks were shown in Supplementary Figure S5, from which we observed that the majority of edge weights located within the interval [10−4, 10−1], and the shapes of corresponding distributions were similar across different tissues.
Calculation of gene-level P-values
We aggregate SNP-level P-values into gene-level P-values using the method PASCAL (Lamparter et al., 2016). In detail, we first extend the annotated region of a gene by 50 kb upstream and downstream and assign an SNP to the gene if the SNP located within the extended region. SNPs outside the surrounding 50 kb regions of a gene are ignored. Then, given a total of S SNPs assigned to the gene, with their P-values obtained from a GWAS data set denoted as , we calculate a test statistic , where is the inverse normal transformation of (i.e. with being the cumulative distribution of the standard normal distribution), is the eigenvalue of the pairwise correlation matrix of the SNPs, derived from such public data sources as the 1000 Genomes Project (1000 Genomes Project Consortium, 2012), and is the Chi-squared distribution with one degree of freedom. The corresponding P-value for the gene can then be calculated accordingly. Note that population structure or other factors that may lead to spurious associations should be adjusted for SNP-level P-values with such methods as linear mixed model (Zhou and Stephens, 2012) or principal component analysis (Patterson et al., 2006) before using our method.
MRF for network integration
For a total of tissue-specific gene regulatory networks, each having genes, we represent the () gene regulatory network by a weighted matrix with being the edge weight between gene and gene in the network, and we use a tensor to denote the collection of all the weight matrices. Here, we ignore the directionality of the input gene networks, if existed, and use the weighted matrix to represent an undirected gene network. Note that our method is also applicable to a single gene network, in which case . These tissue-specific gene regulatory networks share the same set of genes and differ with regard to the connectivity patterns between genes. For gene , we introduce a hidden indicator variable to indicate the association status of the gene with the phenotype of interest, where denotes the existence of the association and otherwise. Following the literature (Chung et al., 2014; Li and Kellis, 2016), we specify that the gene-level P-value follows a mixture of beta distribution given the hidden indicator variable , say,
| (1) |
where accounts for the inflation of the P-values from the null distribution, which has been commonly observed in real data.
Let collects all hidden indicator variables and denotes all gene-level P-values. We assume that the association status of the genes is not independent, i.e. connected genes tend to have similar association status in the networks of phenotype-relevant tissues. In order to capture such dependence structure, we introduce a MRF prior for the joint distribution of all hidden indicator variables as
| (2) |
where collects all parameters in the MRF, denotes the partition function, and the indicator function that equals to one when the inside condition is satisfied. Due to the intractability of the partition function , we approximate the joint distribution of using the pseudo-likelihood approach (Besag, 1986), as
| (3) |
where denotes the association status of all genes except for gene , and the conditional probability of given parameters and can be derived as
| (4) |
where be the sigmoid function, with denoting the neighboring statistics for gene in the network.
For Bayesian inference, we specify a gamma distribution Gamma(1,1) as the conjugate prior for and , a normal distribution N(0,10) as the prior for , and a spike-and-slab prior (George and McCulloch, 1993) for , where both spike and slab parts are normal distributions with different variances. For the tissue-specific network, we assign a binary hidden variable to denote its relevance to the phenotype, where represents the tissue is relevant to the phenotype and otherwise. The conditional distribution of given according to the spike-and-slab prior is specified as
| (5) |
where is a fixed hyper-parameter (set as default), controlling the proportion of relevant tissues with nonzero , another fixed hyper-parameter (set 100 as default), and denotes the inverse gamma distribution. Let the binary vector collect all hidden indicator variables for tissue relevance.
Parameter estimation via Bayesian inference
We derive a Gibbs sampling algorithm for Bayesian inference of both model parameters and hidden variables. With the likelihood and the prior specified, we derive the joint posterior distribution of model parameters and hidden variables as
| (6) |
The parameters and are updated as
| (7) |
where means conditioning on the anything else, and indexes the number of iterations. The parameter is updated as
| (8) |
For , we utilized the data augmentation trick proposed in the Bayesian logistic model (Polson et al., 2013) and augmented a Polya-Gamma variable for each gene. The Gibbs updates of and are
| (9) |
where PG stands for the Polya-Gamma distribution. The posterior covariance matrix is , and is the neighboring statistics matrix with the row being . Note that changes during iteration and is computed by . The other matrices are denoted as , and . For , each is updated as
| (10) |
Lastly, each is updated sequentially according to its conditional distribution specified as
| (11) |
Before Gibbs sampling, we adopt a simple model for parameters initialization, as described in Supplementary material.
Statistical inference of phenotype-associated genes and relevant tissues
We have two inference questions of interest: (i) the association status of each gene with the phenotype of interest and (ii) the relevance of each tissue to the phenotype under investigation. To achieve these goals, we simulate the MCMC steps times (20000 as the default). The first half is abandoned as the burn-in period, which is observed to be enough for convergence empirically, and the second half is used to make inference.
For the first question, we test for each gene against the null hypothesis that the gene is not associated with the phenotype of interest. To achieve this, we follow the literature (Newton et al., 2001; Lin et al., 2015) to calculate the posterior probability-based definition of local FDR based on the posterior probability of each gene, as . To control the global FDR, we firstly sort local FDRs of genes in non-decreasing order, with the smallest one denoted as . Then, given a global FDR threshold (e.g. 0.05), we identify
| (12) |
and reject all null hypothesis corresponding to . The inference procedure for relevant tissues can be done in a similar way. To visualize the relevant tissues, we also define the posterior inclusion probability (PIP) for tissue as . Note that the inference procedures for associated genes and relevant tissues are done separately.
Computational complexity and model implementation
Computations involved in our method include parameter estimation and statistical inference, and the majority of time is consumed by the Bayesian inference part. The computational complexity for updating each parameter is , and we have parameters (i.e. ) leading to the complexity of for each iteration. Besides, in each iteration, we have to pay the complexity and for updating the hidden variables and . Therefore, the overall complexity of our model is , where is the number of iterations for MCMC sampling. We used R to implement our model and resorted to Rcpp (Eddelbuettel et al., 2011) for fast sampling of the hidden variables . Empirically, the whole process could be finished within several hours for whole-genome analysis with a main stream laptop.
Supplementary material
Supplementary material is available at Journal of Molecular Cell Biology online.
Funding
This work was supported by the U.S. National Institutes of Health (R01HG007834 and R01GM109836), the National Natural Science Foundation of China (61721003, 61573207, 61175002, 61561146396, and 61673241), the Recruitment Program of Global Experts of China, and Tsinghua National Laboratory for Information Science and Technology.
Conflict of interest: none declared.
Author contributions: W.H.W., T.C., and R.J. designed this project. M.W. conducted all experiments. Z.L. and S.M. helped with statistical modeling and data processing. M.W., R.J., and W.H.W. wrote the manuscript. All authors read and approved the final manuscript.
Supplementary Material
Acknowledgements
We appreciate the China Scholarship Council (CSC) for supporting Mengmeng Wu’s living expenses while visiting Stanford University.
References
- 1000 Genomes Project Consortium. (2012). An integrated map of genetic variation from 1,092 human genomes. Nature 491, 56–65. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Allen H.L., Estrada K., Lettre G., et al. (2010). Hundreds of variants clustered in genomic loci and biological pathways affect human height. Nature 467, 832–838. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Altshuler D., Daly M.J., and Lander E.S. (2008). Genetic mapping in human disease. Science 322, 881–888. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Anderson C.A., Boucher G., Lees C.W., et al. (2011). Meta-analysis identifies 29 additional ulcerative colitis risk loci, increasing the number of confirmed associations to 47. Nat. Genet. 43, 246–252. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Andersson R., Gebhard C., Miguel-Escalada I., et al. (2014). An atlas of active enhancers across human cell types and tissues. Nature 507, 455–461. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Ashley E.A. (2016). Towards precision medicine. Nat. Rev. Genet. 17, 507–522. [DOI] [PubMed] [Google Scholar]
- Baigent C., Landray M.J., Reith C., et al. (2011). The effects of lowering LDL cholesterol with simvastatin plus ezetimibe in patients with chronic kidney disease (Study of Heart and Renal Protection): a randomised placebo-controlled trial. Lancet 377, 2181–2192. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Barrett J.C., Clayton D.G., Concannon P., et al. (2009). Genome-wide association study and meta-analysis find that over 40 loci affect risk of type 1 diabetes. Nat. Genet. 41, 703–707. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Besag J. (1986). On the statistical analysis of dirty pictures. J. R. Stat. Soc. Series B Stat. Methodol. 48, 259–302. [Google Scholar]
- Calabrese G.M., Mesner L.D., Stains J.P., et al. (2017). Integrating GWAS and co-expression network data identifies bone mineral density genes SPTBN1 and MARK3 and an osteoblast functional module. Cell Syst. 4, 46–59. e44. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Cantor R.M., Lange K., and Sinsheimer J.S. (2010). Prioritizing GWAS results: a review of statistical methods and recommendations for their application. Am. J. Hum. Genet. 86, 6–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chen M., Cho J., and Zhao H. (2011). Incorporating biological pathways via a Markov random field model in genome-wide association studies. PLoS Genet. 7, e1001353. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Chung D., Yang C., Li C., et al. (2014). GPA: a statistical approach to prioritizing GWAS results by integrating pleiotropy and annotation. PLoS Genet. 10, e1004787. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Danese S., and Fiocchi C. (2011). Ulcerative colitis. N. Engl. J. Med. 365, 1713–1725. [DOI] [PubMed] [Google Scholar]
- de Lange K.M., Moutsianas L., Lee J.C., et al. (2017). Genome-wide association study implicates immune activation of multiple integrin genes in inflammatory bowel disease. Nat. Genet. 49, 256–261. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Dobrin R., Zhu J., Molony C., et al. (2009). Multi-tissue coexpression networks reveal unexpected subnetworks associated with disease. Genome Biol. 10, R55. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Duren Z., Chen X., Jiang R., et al. (2017). Modeling gene regulation from paired expression and chromatin accessibility data. Proc. Natl Acad. Sci. USA 114, E4914–E4923. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Eddelbuettel D., François R., Allaire J., et al. (2011). Rcpp: Seamless R and C++ integration. J. Stat. Softw. 40, 1–18. [Google Scholar]
- Estrada K., Styrkarsdottir U., Evangelou E., et al. (2012). Genome-wide meta-analysis identifies 56 bone mineral density loci and reveals 14 loci associated with risk of fracture. Nat. Genet. 44, 491–501. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Firestein G.S. (2003). Evolving concepts of rheumatoid arthritis. Nature 423, 356–361. [DOI] [PubMed] [Google Scholar]
- Franke A., McGovern D.P., Barrett J.C., et al. (2010). Genome-wide meta-analysis increases to 71 the number of confirmed Crohn’s disease susceptibility loci. Nat. Genet. 42, 1118–1125. [DOI] [PMC free article] [PubMed] [Google Scholar]
- George E.I., and McCulloch R.E. (1993). Variable selection via Gibbs sampling. J. Am. Stat. Assoc. 88, 881–889. [Google Scholar]
- Gerstein M.B., Kundaje A., Hariharan M., et al. (2012). Architecture of the human regulatory network derived from ENCODE data. Nature 489, 91–100. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Greene C.S., Krishnan A., Wong A.K., et al. (2015). Understanding multicellular function and disease with human tissue-specific networks. Nat. Genet. 47, 569–576. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Hamosh A., Scott A.F., Amberger J.S., et al. (2005). Online Mendelian Inheritance in Man (OMIM), a knowledgebase of human genes and genetic disorders. Nucleic Acids Res. 33, D514–D517. [DOI] [PMC free article] [PubMed] [Google Scholar]
- He D., Liu Z.-P., Honda M., et al. (2012). Coexpression network analysis in chronic hepatitis B and C hepatic lesions reveals distinct patterns of disease progression to hepatocellular carcinoma. J. Mol. Cell Biol. 4, 140–152. [DOI] [PubMed] [Google Scholar]
- Heckers S., and Konradi C. (2002). Hippocampal neurons in schizophrenia. J. Neural. Transm. 109, 891–905. [DOI] [PMC free article] [PubMed] [Google Scholar]
- International Multiple Sclerosis Genetics Consortium, and Wellcome Trust Case Control Consortium 2. (2011). Genetic risk and a primary role for cell-mediated immune mechanisms in multiple sclerosis. Nature 476, 214–219. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Jiang R. (2015). Walking on multiple disease-gene networks to prioritize candidate genes. J. Mol. Cell Biol. 7, 214–230. [DOI] [PubMed] [Google Scholar]
- Johnson J., Duick D., Chui M., et al. (2009). Identifying prediabetes using fasting insulin levels. Endocr. Pract. 16, 47–52. [DOI] [PubMed] [Google Scholar]
- Juraeva D., Haenisch B., Zapatka M., et al. (2014). Integrated pathway-based approach identifies association between genomic regions at CTCF and CACNB2 and schizophrenia. PLoS Genet. 10, e1004345. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kamburov A., Pentchev K., Galicka H., et al. (2011). ConsensusPathDB: toward a more complete picture of cell biology. Nucleic Acids Res. 39, D712–D717. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Kellis M., Wold B., Snyder M.P., et al. (2014). Defining functional DNA elements in the human genome. Proc. Natl Acad. Sci. USA 111, 6131–6138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lamparter D., Marbach D., Rueedi R., et al. (2016). Fast and rigorous computation of gene and pathway scores from SNP-based summary statistics. PLoS Comput. Biol. 12, e1004714. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Landrum M.J., Lee J.M., Benson M., et al. (2016). ClinVar: public archive of interpretations of clinically relevant variants. Nucleic Acids Res. 44, D862–D868. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Li Y., and Kellis M. (2016). Joint Bayesian inference of risk variants and tissue-specific epigenomic enrichments across multiple complex human diseases. Nucleic Acids Res. 44, e144–e144. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Z., Li M., Sestan N., et al. (2016). A Markov random field-based approach for joint estimation of differentially expressed genes in mouse transcriptome data. Stat. Appl. Genet. Mol. Biol. 15, 139–150. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Lin Z., Sanders S.J., Li M., et al. (2015). A markov random field-based approach to characterizing human brain development using spatial–temporal transcriptome data. Ann. Appl. Stat. 9, 429. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J.Z., van Sommeren S., Huang H., et al. (2015). Association analyses identify 38 susceptibility loci for inflammatory bowel disease and highlight shared genetic risk across populations. Nat. Genet. 47, 979–986. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Liu J., Wan X., Ma S., et al. (2016). EPS: an empirical Bayes approach to integrating pleiotropy and tissue-specific information for prioritizing risk genes. Bioinformatics 32, 1856–1864. [DOI] [PubMed] [Google Scholar]
- Manolio T.A., Collins F.S., Cox N.J., et al. (2009). Finding the missing heritability of complex diseases. Nature 461, 747–753. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Marbach D., Lamparter D., Quon G., et al. (2016). Tissue-specific regulatory circuits reveal variable modular perturbations across complex diseases. Nat. Methods 13, 366–370. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Maurano M.T., Humbert R., Rynes E., et al. (2012). Systematic localization of common disease-associated variation in regulatory DNA. Science 337, 1190–1195. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Mooney M.A., Nigg J.T., McWeeney S.K., et al. (2014). Functional and genomic context in pathway analysis of GWAS data. Trends Genet. 30, 390–400. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Morris A.P., Voight B.F., Teslovich T.M., et al. (2012). Large-scale association analysis provides insights into the genetic architecture and pathophysiology of type 2 diabetes. Nat. Genet. 44, 981. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Neurath M.F. (2014). Cytokines in inflammatory bowel disease. Nat. Rev. Immunol. 14, 329–342. [DOI] [PubMed] [Google Scholar]
- Newton M.A., Kendziorski C.M., Richmond C.S., et al. (2001). On differential variability of expression ratios: improving statistical inference about gene expression changes from microarray data. J. Computat. Biol. 8, 37–52. [DOI] [PubMed] [Google Scholar]
- Nielsen O., Kirman I., Rüdiger N., et al. (2003). Upregulation of interleukin-12 and-17 in active inflammatory bowel disease. Scand. J. Gastroenterol. 38, 180–185. [DOI] [PubMed] [Google Scholar]
- Ott C., and Schölmerich J. (2013). Extraintestinal manifestations and complications in IBD. Nat. Rev. Gastroenterol. Hepatol. 10, 585–595. [DOI] [PubMed] [Google Scholar]
- Pantelis C., Yücel M., Wood S.J., et al. (2005). Structural brain imaging evidence for multiple pathological processes at different stages of brain development in schizophrenia. Schizophr. Bull. 31, 672–696. [DOI] [PubMed] [Google Scholar]
- Patterson N., Price A.L., and Reich D. (2006). Population structure and eigenanalysis. PLoS Genet. 2, e190. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pers T.H., Karjalainen J.M., Chan Y., et al. (2015). Biological interpretation of genome-wide association studies using predicted gene functions. Nat. Commun. 6, 5890. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pickrell J.K. (2014). Joint analysis of functional genomic data and genome-wide association studies of 18 human traits. Am. J. Hum. Genet. 94, 559–573. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Pierson E., Koller D., Battle A., et al. (2015). Sharing and specificity of co-expression networks across 35 human tissues. PLoS Comput. Biol. 11, e1004220. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Piñero J., Bravo À., Queralt-Rosinach N., et al. (2017). DisGeNET: a comprehensive platform integrating information on human disease-associated genes and variants. Nucleic Acids Res. 45, D833–D839. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Polson N.G., Scott J.G., and Windle J. (2013). Bayesian inference for logistic models using Pólya–Gamma latent variables. J. Am. Stat. Assoc. 108, 1339–1349. [Google Scholar]
- Prokopenko I., Poon W., Mägi R., et al. (2014). A central role for GRB10 in regulation of islet function in man. PLoS Genet. 10, e1004235. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Rath A., Olry A., Dhombres F., et al. (2012). Representation of rare diseases in health information systems: the Orphanet approach to serve a wide range of end users. Hum. Mutat. 33, 803–808. [DOI] [PubMed] [Google Scholar]
- Ripke S., O’Dushlaine C., Chambert K., et al. (2013). Genome-wide association analysis identifies 13 new risk loci for schizophrenia. Nat. Genet. 45, 1150–1159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Saha S., Chant D., and McGrath J. (2007). A systematic review of mortality in schizophrenia: is the differential mortality gap worsening over time? Arch. Gen. Psychiatry 64, 1123–1131. [DOI] [PubMed] [Google Scholar]
- Saniabadi A.R., Tanaka T., Ohmori T., et al. (2014). Treating inflammatory bowel disease by adsorptive leucocytapheresis: a desire to treat without drugs. World J. Gastroenterol. 20, 9699. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Scheid R., and Teich N. (2007). Neurologic manifestations of ulcerative colitis. Eur. J. Neurol. 14, 483–493. [DOI] [PubMed] [Google Scholar]
- Scott R.A., Lagou V., Welch R.P., et al. (2012). Large-scale association analyses identify new loci influencing glycemic traits and provide insight into the underlying biological pathways. Nat. Genet. 44, 991–1005. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharan R., Ulitsky I., and Shamir R. (2007). Network-based prediction of protein function. Mol. Syst. Biol. 3, 88. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sharif S., Arreaza G.A., Zucker P., et al. (2001). Activation of natural killer T cells by α-galactosylceramide treatment prevents the onset and recurrence of autoimmune type 1 diabetes. Nat. Med. 7, 1057–1062. [DOI] [PubMed] [Google Scholar]
- Soranzo N., Rivadeneira F., Chinappen-Horsley U., et al. (2009). Meta-analysis of genome-wide scans for human adult stature identifies novel Loci and associations with measures of skeletal frame size. PLoS Genet. 5, e1000445. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Sospedra M., and Martin R. (2005). Immunology of multiple sclerosis. Annu. Rev. Immunol. 23, 683–747. [DOI] [PubMed] [Google Scholar]
- Speliotes E.K., Willer C.J., Berndt S.I., et al. (2010). Association analyses of 249,796 individuals reveal 18 new loci associated with body mass index. Nat. Genet. 42, 937–948. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Spitz F., and Furlong E.E. (2012). Transcription factors: from enhancer binding to developmental control. Nat. Rev. Genet. 13, 613. [DOI] [PubMed] [Google Scholar]
- Stahl E.A., Raychaudhuri S., Remmers E.F., et al. (2010). Genome-wide association study meta-analysis identifies seven new rheumatoid arthritis risk loci. Nat. Genet. 42, 508–514. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Su Z.-D., Sheng Q.-H., Li Q.-R., et al. (2014). De novo identification and quantification of single amino-acid variants in human brain. J. Mol. Cell Biol. 6, 421–433. [DOI] [PubMed] [Google Scholar]
- Szklarczyk D., Morris J.H., Cook H., et al. (2017). The STRING database in 2017: quality-controlled protein–protein association networks, made broadly accessible. Nucleic Acids Res. 45, D362–D368. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Taşan M., Musso G., Hao T., et al. (2015). Selecting causal genes from genome-wide association studies via functionally coherent subnetworks. Nat. Methods 12, 154–159. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Teslovich T.M., Musunuru K., Smith A.V., et al. (2010). Biological, clinical and population relevance of 95 loci for blood lipids. Nature 466, 707–713. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Tobias D.K., Pan A., Jackson C.L., et al. (2014). Body-mass index and mortality among adults with incident type 2 diabetes. N. Engl. J. Med. 370, 233–244. [DOI] [PMC free article] [PubMed] [Google Scholar]
- van der Pouw Kraan T.C., Zwiers A., Mulder C.J., et al. (2009). Acute experimental colitis and human chronic inflammatory diseases share expression of inflammation-related genes with conserved Ets2 binding sites. Inflamm. Bowel Dis. 15, 224–235. [DOI] [PubMed] [Google Scholar]
- Visscher P.M., Brown M.A., McCarthy M.I., et al. (2012). Five years of GWAS discovery. Am. J. Hum. Genet. 90, 7–24. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher P.M., Wray N.R., Zhang Q., et al. (2017). 10 years of GWAS discovery: biology, function, and translation. Am. J. Hum. Genet. 101, 5–22. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Visscher P.M., and Yang J. (2016). A plethora of pleiotropy across complex traits. Nat. Genet. 48, 707–708. [DOI] [PubMed] [Google Scholar]
- Wei P., and Pan W. (2012). Bayesian joint modeling of multiple gene networks and diverse genomic data to identify target genes of a transcription factor. Ann. Appl. Stat. 6, 334. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weinberger D.R. (1987). Implications of normal brain development for the pathogenesis of schizophrenia. Arch. Gen. Psychiatry 44, 660–669. [DOI] [PubMed] [Google Scholar]
- Welter D., MacArthur J., Morales J., et al. (2014). The NHGRI GWAS Catalog, a curated resource of SNP-trait associations. Nucleic Acids Res. 42, D1001–D1006. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Weyer C., Bogardus C., Mott D.M., et al. (1999). The natural history of insulin secretory dysfunction and insulin resistance in the pathogenesis of type 2 diabetes mellitus. J. Clin. Invest. 104, 787–794. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Wu Y., Yao Y.-G., and Luo X.-J. (2017). SZDB: a database for schizophrenia genetic research. Schizophr. Bull. 43, 459–471. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Yang J., Benyamin B., McEvoy B.P., et al. (2010). Common SNPs explain a large proportion of the heritability for human height. Nat. Genet. 42, 565–569. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zammit S., Rasmussen F., Farahmand B., et al. (2007). Height and body mass index in young adulthood and risk of schizophrenia: a longitudinal study of 1 347 520 Swedish men. Acta Psychiatr. Scand. 116, 378–385. [DOI] [PubMed] [Google Scholar]
- Zhang C., Liu C., Cao S., et al. (2015). Elucidation of drivers of high-level production of lactates throughout a cancer development. J. Mol. Cell Biol. 7, 267–279. [DOI] [PubMed] [Google Scholar]
- Zhang A., Xu M., and Mo Y.-Y. (2014). Role of the lncRNA–p53 regulatory network in cancer. J. Mol. Cell Biol. 6, 181–191. [DOI] [PMC free article] [PubMed] [Google Scholar]
- Zhou X., and Stephens M. (2012). Genome-wide efficient mixed-model analysis for association studies. Nat. Genet. 44, 821–824. [DOI] [PMC free article] [PubMed] [Google Scholar]
Associated Data
This section collects any data citations, data availability statements, or supplementary materials included in this article.