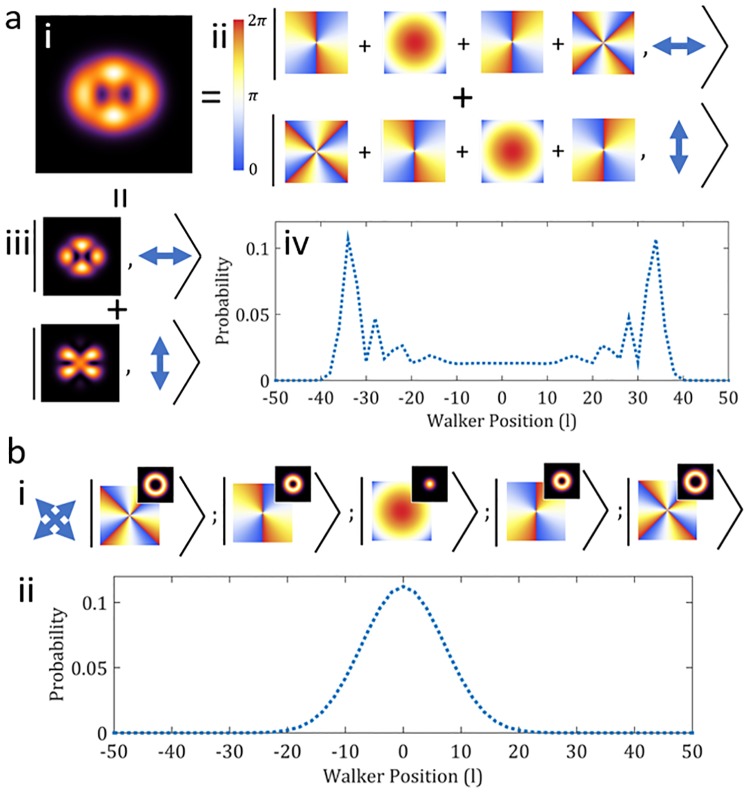
Fig 1. Classically entangled light.

Illustration of the QW reliance upon the non-separability of OAM and polarization states of classical light. (a) shows the non-separable superposition of OAM states and polarization for a 4 step QW. False color density plots (ii) show the phase distribution of the OAM modes l = {-4, -2, 0, 2, 4}, forming the positions occupied by the walker (light beam). Weighted superpositions of these would then yield the spatial modes shown in (iii) with the associated polarization states. Together, the spatial distribution in (i) is formed, where the QW is contained in a single beam of classically entangled light. After many steps, the walker occupies positions near the end of the distribution with greater probability as is shown for 50 steps of a symmetrical walk (iv). (b) shows the 4-step classical RW analogue where the walker may only assume one position (OAM) state at a time. Here, the state of the walker remains separable. Accordingly, the light beam (walker) contains only one of the possible OAM states shown as with different kets and a separable polarization state (i). Insets show the spatial distribution of the beam for each case. (ii) measurements of the repeated walk then results in a probability distribution after 50 steps where the walker occupies positions at the center with the greatest probability.