Abstract
Collagen fibers are the primary structural elements that define many soft-tissue structure and mechanical function relationships, so that quantification of collagen organization is essential to many disciplines. Current tissue-level collagen fiber imaging techniques remain limited in their ability to quantify fiber organization at macroscopic spatial scales and multiple time points, especially in a non-contacting manner, requiring no modifications to the tissue, and in near real-time. Our group has previously developed polarized spatial frequency domain imaging (pSFDI), a reflectance imaging technique that rapidly and non-destructively quantifies planar collagen fiber orientation in superficial layers of soft tissues over large fields-of-view. In this current work, we extend the light scattering models and image processing techniques to extract a critical measure of the degree of collagen fiber alignment, the normalized orientation index (NOI), directly from pSFDI data. Electrospun fiber samples with architectures similar to many collagenous soft tissues and known NOI were used for validation. An inverse model was then used to extract NOI from pSFDI measurements of aortic heart valve leaflets and clearly demonstrated changes in degree of fiber alignment between opposing sides of the sample. These results show that our model was capable of extracting absolute measures of degree of fiber alignment in superficial layers of heart valve leaflets with only general a priori knowledge of fiber properties, providing a novel approach to rapid, non-destructive study of microstructure in heart valve leaflets using a reflectance geometry.
Key terms: Polarized light imaging, structured illumination, collagen fiber structure, cylindrical scattering, optical sectioning, wide-field reflectance imaging
Introduction
Although numerous components contribute to soft tissue biomechanics, collagen fibers act as the primary load-bearing structure in most soft tissues16, 37. Collagen fibers are hierarchical structures; a number of single tropocollagen molecules (~1nm in diameter) make up collagen fibrils (~10 – 100nm in diameter) and are subsequently packed into collagen fibers on the order of microns, which are typically the fiber dimension assumed in multi-scale mechanical models of soft tissues such as heart valves3. These fibers exhibit high tensile strength, and therefore, the orientation and uniformity of collagen fiber alignment dictates soft tissue mechanical function across multiple scales15, 23.
Several optical imaging modalities have been used to investigate collagen microstructure based on the anisotropic scattering and fluorescence of light incident on collagen fibers. Common microscopy techniques include polarization sensitive second harmonic generation and polarization sensitive optical coherence tomography, both of which have high sensitivity to fiber structures29, 30, 43. While these techniques can finely resolve collagen fibers in 2D and 3D volumes, they are typically confined to measurements across relatively small regions of interest (< 1cm2). Larger samples can be imaged, but require linear translation stages to supplement the limited lateral field-of-view of the optical scanning system, restricting imaging during tissue deformation experiments. Small angle light scattering (SALS) is another commonly used technique to map wide-field collagen fiber structure in planar tissues such as heart valve leaflets40, 41. However, SALS also requires bidirectional translation of the sample in lieu of optical scanning, also resulting in extensive scanning times (>1 hour per ~5 cm2) even at modest translation steps (200 μm). As a transmission imaging technique, the geometry of SALS precludes distinguishing layered collagen architecture in heart valve leaflets.The chemical optical clearing treatments and physical sectioning required to map the fiber structure in individual layers of heart valve leaflets often limits SALS imaging to mechanical testing endpoints when studying these tissues. Despite these limitations, the wide-field measurements of fiber architecture, including the primary fiber orientation and degree of fiber alignment, are important in developing models of soft-tissue biomechanics39. There is a clear need for a rapid, non-destructive, wide-field reflectance imaging technique to quantify collagen microstructure in heart valve tissues21, 39.
A large volume of work exists in polarized light imaging and Mueller matrix polarimetry of biological tissues17, 26, 31, 38. These techniques allow characterization of the polarimetric properties of tissues, and have been used to relate polarization dependent optical properties to various underlying structural and physiological features17, 38, 44. Importantly, polarized light imaging can be performed in wide-field with readily adjustable fields-of-view, allowing large sample areas to be imaged rapidly at near or above video rate (> 10 Hz)45, 49. However, polarization imaging systems have two inherent challenges. First, these techniques primarily provide polarimetric properties, such as birefringence or depolarization, as a measure of tissue structure. While these metrics are useful for relative comparison of structural anisotropy, absolute measures of fiber orientation distributions, such as those found with SALS, are needed as inputs to constitutive models of soft tissue mechanical behavior39. Extracting absolute measures of degree of fiber alignment with these techniques typically requires precise a priori knowledge of fiber size and optical properties at each image point. As a result, small changes in the fiber size may influence the interpretation of degree of fiber alignment. Second, these systems do not distinguish distinct tissue layers within samples and are instead bulk measurements through the thickness of the sample. Transmissive polarization systems measure average optical anisotropy through the entire sample thickness, while reflective polarization systems average through a sampling depth up to several millimeters deep in biological tissues22. In both cases, the multiple-scattering of the light through thick, turbid samples leads to overall depolarization of the optical signal, resulting in changes of measured optical anisotropy as a function of sampling depth and potential under-estimation of structural anisotropy18. Serial sectioning and imaging is feasible, but again limits measurements of fiber microstructure to experimental endpoints. These issues demonstrate the need to limit optical anisotropy measurements in planar biological tissues to thin, superficial layers (< 500 μm) without physical sectioning. The need for depth-gating of polarization measurements is particularly relevant to heart valve leaflets, which have distinct layers several hundred microns thick that each possess unique fiber structure35, 42.
Polarized spatial frequency domain imaging (pSFDI) was previously introduced by our group as a method to rapidly map fiber structure in whole heart valve leaflets with a reduced imaging depth48. Polarized light imaging provides sensitivity to fiber structure, while structured illumination allows reduction of the effective imaging depth to distinguish superficial tissue layers on the order of several hundred microns thick. Our previous study determined the spatial frequencies required to isolate polarization measurements in superficial layers of heart valve leaflets without physical sectioning; however, this initial study did not attempt to quantify degree of fiber alignment from the pSFDI signal.
Herein, we present an extended theoretical model and experimental validation of pSFDI that allows determination of absolute degrees of fiber alignment. The model is based on polarized light scattering from cylindrical particles, which represent tissue fibers. We simulated a range of cylinders with physiologically relevant sizes and orientation distributions to establish a relationship between optical and structural anisotropy in biological tissues, which was then used to extract absolute measures of degree of fiber alignment from our pSFDI measurements. We validated our model using electrospun fiber scaffolds with known fiber properties determined by electron microscopy. We then examined aortic heart valve leaflets and compared our results to small-angle light scattering images of the same samples. Our improved pSFDI modeling technique demonstrates the ability to rapidly (< 5 seconds) quantify superficial collagen microstructure in heart valve tissues over whole-leaflet fields-of-view (~5 cm2). The speed, system geometry, and non-destructive nature of pSFDI allows assessment of fiber architecture in samples at multiple time points, ultimately paving the way for studies of dynamic fiber structure during active tissue deformation.
Materials and Methods
Instrumentation
The pSFDI system (Figure 1) is composed of three main components: pattern projection, polarization modulation, and image detection. Spatial frequency patterns were projected using a DLP Lightcrafter Evaluation Module digital micro-mirror device (Texas Instruments, Dallas TX). The projected pattern was delivered through a bandpass filter to produce light with a center wavelength of 529 nm and a measured spectral full-width half-maximum of less than 15 nm. The spectrally filtered pattern was folded with a right angle mirror and projected onto the sample through a linear polarizer mounted on a Zaber high speed rotational stage with a 2” aperture (RSB120AD-T3-MC03 Zaber Technologies Inc., Vancouver, BC, Canada). The stage was stepped at 9° increments through 180° for a total of 20 measurements, using the maximum rotational speed of the stage (300 RPM). A CMOS camera (acA1300–60gm, Basler AG, Ahrensburg, Germany) captured an image of each projected spatial pattern through the same linear polarizer aperture at each polarizer orientation. The image resolution was 1280×1024 pixels, and the field of view was approximately 24 mm x 18 mm, though this could be increased or decreased for desired applications by changing the working distance of the sample. The imaging system used a f/1.4 variable focus imaging lens (calculated collection half-angle of ψ = 15°) and the camera had an exposure time of 20 ms. The entire system was controlled through a custom LabVIEW VI (National Instruments, Austin TX), and acquisition of one full data set for a single spatial frequency was measured to be less than 5 seconds.
Figure 1 -.
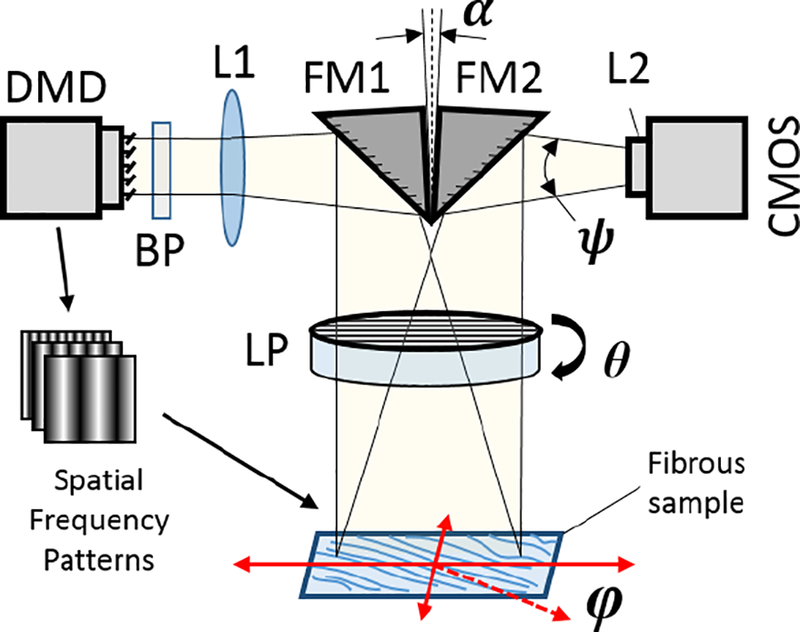
pSFDI System Schematic. Digital Micromirror Device (DMD), Fold Mirrors (FM1 & FM2), Linear Polarizer (LP), Projection & Imaging Lenses (L1 & L2), Bandpass Filter (BP), and CMOS Camera. The fibers in the sample are primarily distributed angularly in the X–Y plane along an angle φ, and the LP rotates in the same plane at angle θ. A small angle α ≈ 10° between the fold mirrors allows the projection and imaging fields of view to align. The working distance from the sample is adjustable from 1 cm – 20 cm from the LP, and can be adjusted to alter the system field-of-view.
Spatial frequency domain imaging
Spatial frequency domain imaging (SFDI) is a wide-field imaging technique that has been described extensively elsewhere8, 10. Briefly, SFDI allows recovery of reflectance in the spatial frequency domain by demodulation of spatial patterns that are projected onto a sample. In practice, a sinusoidal pattern with a known spatial frequency fx is projected onto a sample. This spatial frequency pattern is shifted in phase twice by 120° and the sample is imaged at each phase, resulting in three total images (I0°, I120°, I240°). These three images are then demodulated into what are commonly referred to as “DC” and “AC” reflectance components, defined mathematically as:
| (1) |
| (2) |
IDC is equivalent to the total reflectance from the sample under planar illumination, while IAC is the spatially modulated reflectance recovered for a given spatial frequency. As fx increases, the modulated reflectance IAC becomes representative of fewer scattering events, and therefore limits the sampling depth of the reflectance signal relative to the sample absorption and scattering9, 10. We use this technique for the purpose of depth-gating in our sample and limiting the sampling depth of our polarization measurements to superficial layers. At low spatial frequencies, the effective sampling depth (d’eff) is related to the optical properties of the tissue and spatial frequency by:
| (3) |
where μα and μ’s are the absorption coefficient and reduced scattering coefficient of the sample. As fx approaches 0 (i.e. planar illumination), d’eff is dictated entirely by the sample’s optical properties. For a fixed set of sample optical properties, d’eff decreases with increasing spatial frequency. However, EQ3 is only valid when the majority of the light has undergone multiple scattering events (i.e. diffuse scattering). For biological tissue, whose absorption and reduced scattering coefficients are on the order of μα ≈ 0.01 mm−1 and μ’s ≈ 1.0 mm−1, EQ3 is only valid for spatial frequencies below about 0.3 mm−1. Numerical methods are required to determine d’eff at higher spatial frequencies, where ballistic photons contribute a significant amount to the measured reflectance. A detailed study of reflectance from diffuse and ballistic scattering by Bodenschatz et al demonstrated that for the spatial frequency used in this study (fx = 0.5mm−1), d’eff is approximately 250μm4. Additionally, as co-polarized imaging gates photons which maintain their initial polarization and therefore have also undergone a low number of scattering events, the effective imaging depth is likely even shallower47.
Polarized light theory & simulation
Mueller matrix system model
We use a Mueller matrix formalism to describe changes in the polarization of light as it travels through our system. In this formalism, Stokes vectors define the polarization state of light at any given point and Mueller matrices describe how both optical elements and the sample alter the Stokes vectors (see Appendix A). We derive the basic mathematical form for our system from an existing model developed by Chenault and Chipman, who described the Mueller matrix representation of the rotating linear polarizer system outlined in the Instrumentation section6. This model is useful due to the simplicity of required instrumentation, the limited number of polarization states required to satisfy the sampling criteria, and the ability to linearize the model for rapid fitting. The basic Mueller matrix representation of the system is expressed in EQ4.
| (4) |
Mp and Rp are the Mueller matrix and rotational matrix for a linear polarizer, Ms is the sample Mueller matrix, and and are the input and output Stokes vectors. An extended description of these Mueller matrices can be found in Appendix A. Non-polarization dependent system efficiencies are captured with the τsys term, which we will omit from this point forward, as it only contributes to linear scaling of the final signal that is accounted for through calibration. The angle θ represents the orientation of the rotating polarizer in our system, and the sample orientation φ is the major axis of optical anisotropy in the sample (i.e., the orientation in which the reflected light intensity is maximized), and the response is symmetric over a period of [−90°, 90°]. Solving this system results in EQ5:
| (5) |
M11, M12, and M33 are the Mueller matrix elements of the sample. The signal in EQ5 can be further simplified into a sum of cosines, seen in EQ6, which is more suitable for fitting to experimental data (Appendix B).
| (6) |
We performed measurements at 9° intervals, resulting in a total of 20 measurements. The signal in EQ6 requires a theoretical minimum of 8 polarizer orientation measurements at 22.5° intervals to satisfy the Nyquist sampling criteria (twice the highest frequency cosine term in EQ6)36. However, as the main imaging bottleneck was from changing the projection pattern, the imaging speed gained by reducing the number of measurements was minimal. We therefore used a larger number of polarizer measurements (20) to decrease sensitivity to noise. The coefficients α0, α2, and α4 describe the amplitude of the signal response as a function of polarizer angle. These are related to the Mueller matrix elements of the sample by the following:
| (7) |
| (8) |
| (9) |
The first term, α0, represents the mean value of the response, which is non-polarization dependent, while the α2 and α4 terms represent the polarization dependent changes in intensity. Subsequently, we define our degree of anisotropy (DOA) metric as the ratio of the polarization-dependent terms to the non-polarization dependent reflectance:
| (10) |
Cylindrical scattering model
The model described in EQ6 is valid for any sample with polarization dependent optical anisotropy. We consider a special case in which the optical anisotropy of the sample originates from infinitely long cylindrical scatterers, which we will use to represent collagen fibers5, 25. The ‘infinitely long’ assumption is valid when the cylinder length is large when compared to its diameter, and therefore appropriate for the tissue fibers we are modeling. The geometry of this type of scattering model is described in Figure 2(a). Linearly polarized light is normally incident onto a cylinder with a fixed direction (φ) defined by the cylinder’s longitudinal axis. As the orientation of the incident linearly polarized light (θ) is rotated with respect to the longitude axis of the cylinder, the intensity of back-scattered light can be calculated by EQ6, as seen in an example intensity response in Figure 2(b).
Figure 2 -.
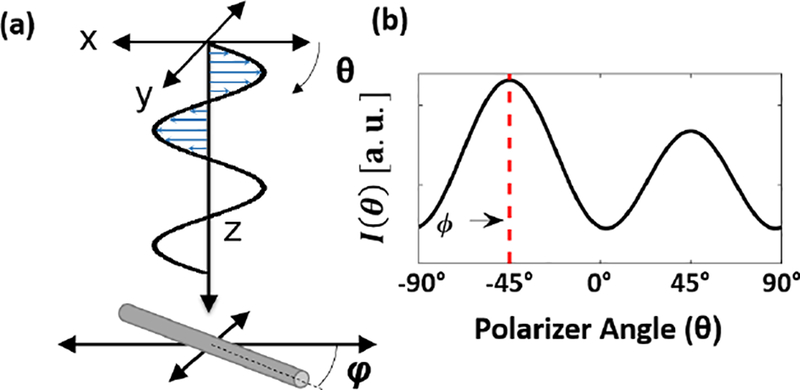
(a) Geometry of model for linearly polarized light incident upon a cylindrical particle. (b) Modeled backscattering for a cylinder with angle φ as a function of the linear polarizer orientation (θ)
The general form of the scattering matrix for light normally incident onto an infinitely long cylinder is shown in EQ11:
| (11) |
where M11, M12, M33, and M34 are derived from the Mie scattering solution to the special case of light incident onto an infinite cylindrical particle5, 25. The null matrix elements, as well as the matrix symmetry, are a result of the assumption that we are only considering a system geometry in which the incident light is normal to the long axis of the cylinders, i.e. the fibers are in the lateral imaging plane of the system. This geometry is appropriate to representing collagen fibers in membranous tissues like heart valve leaflets, where the longitudinal axis of the collagen fibers is oriented primarily within the lateral plane of the image. The inputs required to solve the cylindrical scattering Mueller matrix are the relative index of refraction of the particle and the surrounding media (m = ncyl/nbgd), the radius of the cylinder (rcyl), the wavelength of incident light (λ), and the collection angle of the imaging system (ψ). The cylinder size, wavelength, and refractive index surrounding the particle are typically combined into the size parameter: x = 2π × nbgd × rcyl/λ.
Extension to fiber distributions
In any real physical sample, there exists a fiber orientation distribution function (ODF) describing the occurrence of fibers in a given direction. The optical signal from fiber populations is therefore a weighted sum of the scattering contributions from each of the individual fibers in a given orientation. Mathematically, this can be represented as an integral of the scattering function for a single fiber multiplied by the weights defined by the fiber ODF:
| (12) |
The selection of an appropriate probability density function (PDF) was critical to modeling the fiber populations for the simulation and to fit to the electrospun fiber ODFs extracted using scanning electron microscopy (SEM) accurately. We iterated through several different types of fiber distributions while developing our computational model space, primarily based on the best fits of real fiber distributions characterized with SEM for the electrospun fiber samples. Two circular distributions (wrapped Cauchy and von Mises) were initial candidates but did not fit the ODFs from the SEM data well27. Instead, we model and fit the fiber ODFs using a mixed Cauchy probability density function (PDFMC), which is described in EQ137.
| (13) |
In this function, c describes the shape of the distribution peak, d is the ratio of random fibers to non-random fibers, and φ indicates the mean fiber angle. The c parameter is bound from [0, ∞], with 0 indicating no fiber variance. The d parameter has bounds from [0, 1], with 1 indicating entirely random fibers. We use this modified Cauchy PDF due to its robustness in fitting a wide range of ODFs found in real tissue and fiber samples. However, because the c and d parameters obfuscate physical meaning about the degree of fiber alignment, we will instead use the normalized orientation index (NOI) to singularly describe the fiber variance:
| (14) |
Here, Φ50% represents the angular width of the distribution containing 50% of the total ODF (or PDF). In a completely random distribution, Φ50% =90°, so the NOI has a range from [0, 100]. Variations of this orientation distribution metric have been used in several studies which show its utility for informing mechanical models that incorporate fiber structure2, 7, 11, 19, 28. An example simulation of the impact of degree of fiber alignment, as characterized by NOI, on the polarized light signal can be seen in Figure 3. The polarization dependent response is maximized when the fibers are perfectly aligned in one direction (NOI = 100). However, as NOI decreases, the polarization dependent response is damped, as seen by the decrease in the amplitude of the response curve. When the fibers are uniformly randomly aligned (NOI = 0), the polarization dependent response disappears entirely. Subsequently, the extracted DOA metric, which is a ratio of the polarization dependent response to the non-polarization dependent response, will decrease as NOI decreases. The exact mathematical form of the relationship between NOI and DOA, which allows conversion between measures of structural anisotropy and optical anisotropy, is discussed in the Results: Simulations section.
Figure 3 -.
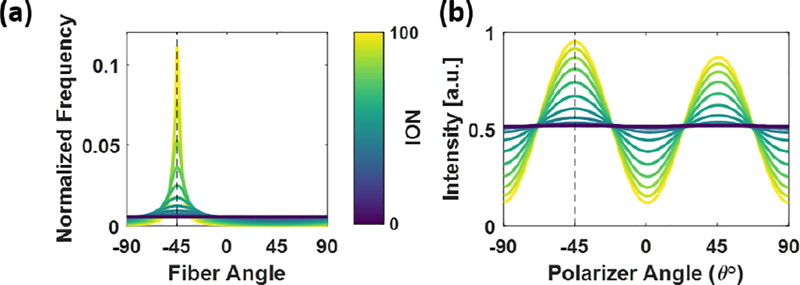
(a) Example modified Cauchy fiber PDF as a function of Normalized Orientation Index (NOI); increasing NOI corresponds to higher alignment of the fibers. (b) Simulation of polarization dependent scattering response to changes in fiber anisotropy, showing the amplitude of the polarization dependent intensity decreasing as a function of decreasing NOI.
Simulations
We performed two separate simulations: the first to confirm the accuracy of our model, and the second to examine the relationship between fiber orientation distributions and optical anisotropy measured with pSFDI. In the first simulation, we used our model to predict DOA for a set of electrospun fiber samples. The known fiber sizes and orientation distribution functions for each polycaprolactone (PCL) fiber phantom, as described in the Methods: Electrospun Fiber Phantom Imaging section, were used as inputs to the simulation, along with the known refractive indices for PCL and water at a wavelength of λ = 529 nm (nfib = 1.45 – 1.49, nbgd = 1.33)32. In the second simulation, we calculated expected DOA from cylindrical fibers across a large range of physiologically relevant size parameters (x) and relative refractive indices (m). The fiber sizes we simulated were based on the expected range of collagen fiber radii found in recent studies of heart valve tissue3. The relative refractive index included a range relevant to hydrated collagen in interstitial fluid (nfib = 1.38 – 1.42, nbag = 1.33 – 1.35)46. We then performed a convolution of the results with the modified Cauchy fiber PDF discussed in the previous section. The PDF parameter ranges were based on those relevant to biological tissue as well as those found for the electrospun fiber phantoms3. The parameter range for the second simulation can be found in Table 1.
Table 1 -.
Polarized light model simulation parameter space. The ranges for size parameter, relative refractive index, and distribution parameters were determined from previous studies of collagenous soft tissues.
| Parameter | Minimum | Maximum | # | Spacing |
|---|---|---|---|---|
| Fiber radii (rcyl) | 50 nm | 1000 nm | 1173 | Logarithmic |
| Relative Refractive Index (m) | 1.005 | 1.12 | 21 | Linear |
| Distribution parameter (c) | 10−2 | 100.5 | 25 | Logarithmic |
| Randomness parameter (d) | 0.4 | 1 | 25 | Linear |
| Normalized Orientation Index (NOI) | 0 | 100 | 625 | N/A |
Electrospun fiber phantom imaging
To validate our model experimentally, we fabricated electrospun fiber phantoms that varied in degree of fiber alignment using a custom-made electrospinning mandrel1. The electrospinning process has been used previously to construct tissue scaffolds with a controllable degree of microfiber alignment, mimicking tissue microstructure1, 7, 12, 13. To create these phantoms, a 10% (wt/vol) solution of PCL was dissolved in hexafluoroisopropanol. This solution was ejected from a needle charged to 5 kV onto a grounded, rotating aluminum mandrel. The working distance from the needle to the mandrel was 11 cm, and the fibers were collected for one hour to produce approximately 150 – 250 μm thick samples. It should be noted that the optical thickness of these samples is much greater than tissue due to the increased relative refractive index between PCL and the background medium (water), and therefore the sampling depth of the pSFDI system is shallower than the total thickness of the electrospun fiber samples4. We collected six phantoms with a range of fiber alignments by varying the rotational velocity of the mandrel from 0 – 2500 RPM in 500 RPM intervals. The samples were cut into squares approximately 1 cm2, bathed in dilutions of ethanol and distilled water to decrease hydrophobicity, and then imaged with pSFDI in a pure distilled water bath. After pSFDI imaging, the same samples were dried and sputter coated with 15 nm of platinum/palladium nanoparticles. The samples were each imaged at nine locations evenly spaced across the entire sample surface at 1000X magnification with a scanning electron microscope (Super40-SEM, Zeiss, Oberkochen Germany). The fiber orientations in the SEM images were analyzed and averaged across each sample using a custom image processing routine based on a Fourier domain fiber orientation analysis technique developed by Mega et al34. Our analysis indicated a range of NOI from ~[10, 50] was achieved for the samples (Figure 4). The distribution of fiber diameters were found from the same image set using the DiameterJ plugin for ImageJ (NIH, Bethesda MD)24.
Figure 4 -.
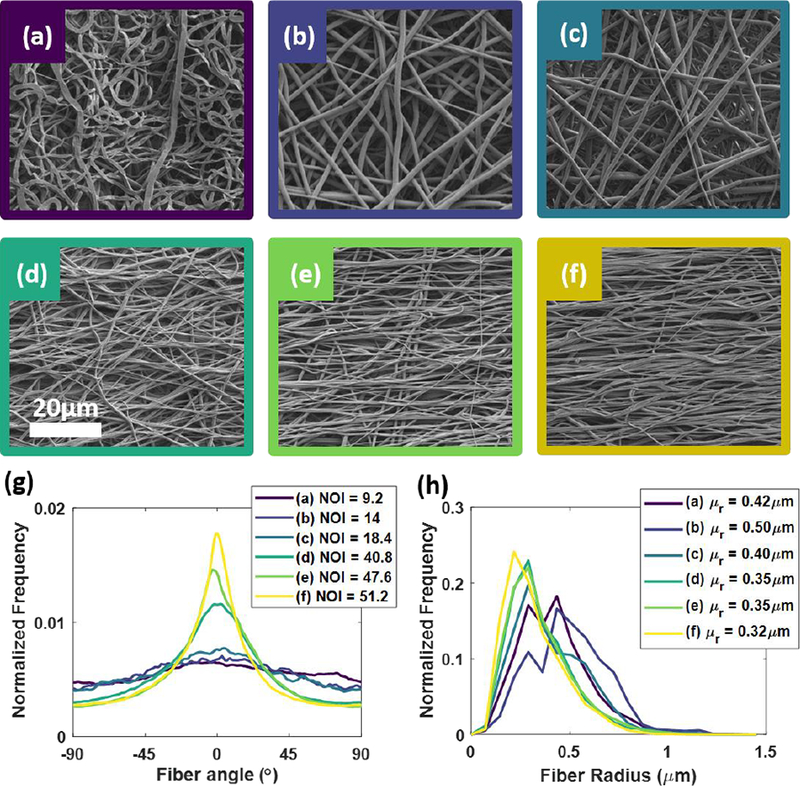
(a–f) SEM images of electrospun fibers collected at different rotational speeds. (g) Extracted orientation distribution functions (ODF) at each collection speed along with calculated normalized orientation index (NOI). (h) The less aligned samples had slightly larger fiber radii, although all were relatively similar.
Aortic heart valve leaflet imaging
Collagen fiber structure in leaflets of the aortic valve has been well studied. In addition to regional variations along the surface of the leaflets, there are multiple layers that have been shown to have distinct microstructure and mechanical properties33, 35, 42. The fibrosa is an outer layer which is responsible for most of the structural integrity of the valve; a substantial number of regularly-aligned collagen fibers are oriented orthotropically along the circumferential direction of the valve35. The outer layer on the opposite side is the ventricularis, which also contains a significant amount of collagen but has less overall organization compared to the fibrosa35. The spongiosa is often described as a transition region between the two outer layers and primarily contains water mediated by glycosaminoglycans14. Previous histological examinations of aortic leaflet cross-sections have measured average fibrosa and ventricularis layers to be approximately 320 μm and 160 μm, respectively, which is suitable for the depth limitation capabilities of the described pSFDI system42.
A fresh ovine aortic valve leaflet was excised and fixed with glutaraldehyde for 24 hours while pressed between glass slides. The samples were then washed, placed in a bath of phosphate buffered saline and imaged with pSFDI on both sides, allowing comparison of the two outermost layers of the leaflet: the fibrosa and the ventricularis. The same sample was subsequently bathed in dilutions of glycerol and water to optically clear the sample, and then mounted again between glass slides prior to imaging with SALS40. The raw SALS data is considered a direct measure of the full ODF of collagen fibers within the beam diameter (250 μm) at each pixel point, from which the primary fiber orientation and NOI were calculated using the same definition in EQ1428, 40. The images from pSFDI and SALS were all co-registered by binarizing the raw intensity images for each data set and using the Matlab function imregtform, limiting the transformation to rotation and translation. The SALS images were additionally up-sampled to match the pSFDI data in pixel resolution, though it should be noted that this did not result in any real increase in resolution. Any rotational transformations applied during registration were subsequently accounted for in the final fiber orientation maps.
It should be noted that the glutaraldehyde fixation protocol was not necessary for either imaging technique, but was instead performed to ensure repeatability of degree of fiber alignment measurements between the two techniques. Though this treatment may alter the native microstructure, as the collagen fibers are cross-linked, the goal of this experiment was to allow comparison between the two imaging techniques, and as such it was required that the microstructure was fixed as the sample was transferred between systems. The optical clearing with glycerol, however, was required for the transmissive SALS imaging technique. Our goal in comparing pSFDI data to SALS was to demonstrate the capability of pSFDI to extract comparable metrics of wide-field fiber alignment at higher speeds without the need for physical sectioning of the samples to discern layered architecture.
Image processing
The image data sets were processed using both custom and pre-built functions in Matlab. Each polarization image was first normalized to images of a Spectralon diffuse reference target (Labsphere, North Sutton NH) taken at each polarization state under planar illumination, as well as a dark image with the illumination turned off.
| (15) |
Here, is the demodulated spatial frequency image of the sample, is the planar reflectance image of the calibration standard, Idark is a system image with no illumination, and ref% is the known diffuse reflectance percentage of the calibration standard. This normalization was performed on a per-pixel basis at each polarization angle. The and Idark images were additionally median filtered with a 10×10 pixel window to reduce noise.
This pre-processing routine is necessary to remove light pollution and inherent system polarization from the polarized light image set. During the primary processing, each polarization image set for a single spatial frequency was fit on a per-pixel basis to a modified form of EQ6. This modified form was used to allow linear fitting (Appendix B), and resulted in fitting speeds in excess of 106 pixels per second. The total processing time, including loading images into memory and pre-processing steps, was only two minutes for a single data set.
Results
Electrospun fiber phantoms
The cropped raw images of the electrospun fiber samples are shown in Figure 5(a–f), with the samples corresponding to the same labels in Figure 4(a–f). A 200×200 pixel region of interest, indicated by the red boxes, was used to compute the mean and variance of measured DOA values for each sample.
Figure 5 -.

Raw images of the six fiber samples, with colors and letters corresponding to the same samples in Figure 4. The red box indicates the region of interest over which pSFDI measurements were averaged.
Measured DOA for each sample are compared to the corresponding DOA predicted by our model in Figure 6. Error bars in the y-axis indicate the standard deviations of measured DOA across the region of interest for each sample shown in Figure 5, and error bars in the x-axis indicate the standard deviations of the predicted DOA for each sample based on the range of fiber diameters used for input to the model (from Figure 4). The modeled values showed a much larger variation in the predicted DOA as compared to the measured DOA, which was primarily a result of the oscillatory nature of scattering when the size of the scattering particle is close to the wavelength of incident light. Despite this, the measurements and model showed overall linear agreement: experimental measurements of DOA were all within 16% of the model-predicted values, and were all contained within one standard deviation of the model predicted values.
Figure 6 -.
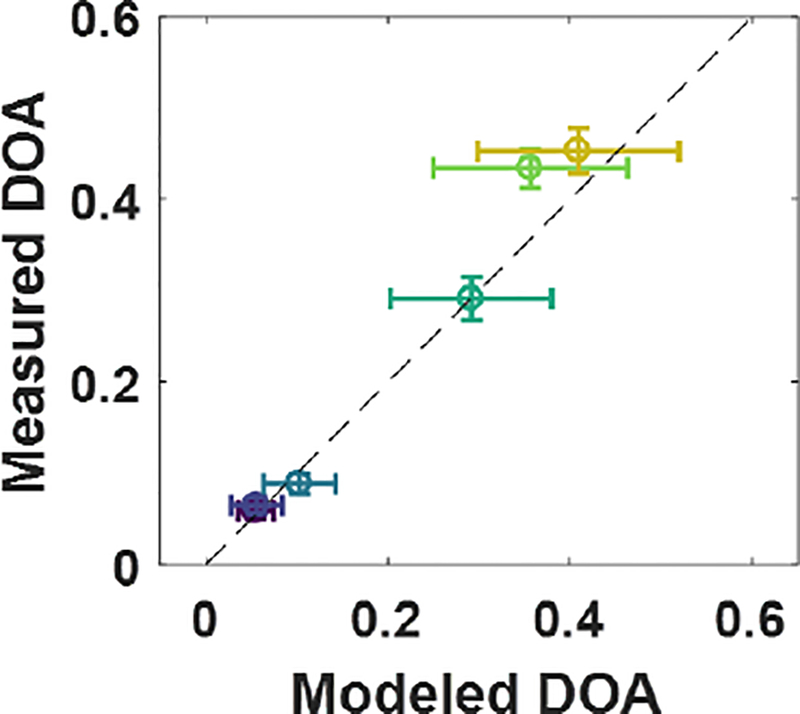
Measured DOA from pSFDI data compared to modeled DOA for the same samples, using known fiber properties as model inputs. Error bars show standard deviations for the model output for the range of fiber properties given for the input (x-axis) and standard deviation of the measured data within the image region of interest (y-axis).
Simulations
Our simulation of a broad range of fiber properties and distributions showed that DOA has a strong linear dependence on NOI. Figure 7 illustrates the simulated DOA as a function of NOI for the range of fiber parameters in Table 1. The shaded area shows the standard deviation around mean DOA at each evaluated NOI, which describes the variation of the model due to the range of fiber sizes and relative refractive indices within the model space. A clear linear trend (DOA = A × NOI) described the model space well (r2 = 0.95). The linear model fit coefficient A was 6.66×10−3. This fit model was subsequently inverted to establish a linear conversion of relative DOA (a measure of optical anisotropy from the pSFDI data) to NOI (a measure of structural anisotropy).
Figure 7 -.
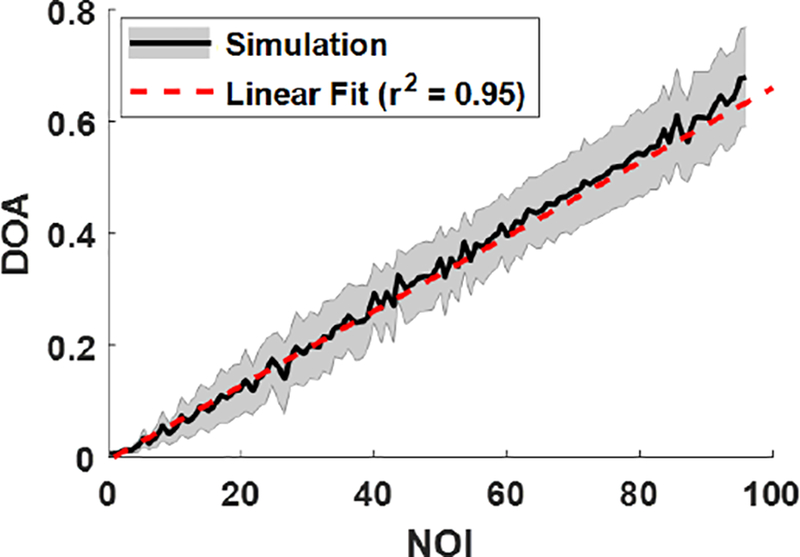
Simulated DOA as a function of NOI, for a range of physiologically relevant fiber distributions, sizes, and relative refractive indices. The shaded region is the standard deviation of simulated DOA at each evaluated NOI value. The linear fit was inverted to estimate NOI as a function of DOA.
Aortic heart valve leaflets
The raw intensity images of the ovine aortic valve leaflet samples matched well among the pSFDI and SALS imaging techniques, showing good registration of morphological features between the three data sets (Figure 8 d–f). For example, the tendon-like tertiary bundles of fibers present in the commissure regions (top right and left corners) were visible in all three sets of images, though they were more readily discernable in the pSFDI images. The higher pixel resolution of the pSFDI images (19 μm) showed these morphological structures more clearly than the accompanying SALS images (250 μm). Fiber orientation (Figure 8, g–i) also matched well between all image sets, and agreed with previous studies of heart valve fiber orientation40, 48. While the fiber orientations were primarily the same, indicating overall consistency in fiber directionality through the thickness of the sample, the NOI maps showed markedly different alignment in opposite sides of the sample in the pSFDI images. Additionally, The SALS-derived NOI values appeared to be much lower overall than the pSFDI-derived values on both sides of the sample.
Figure 8 -.
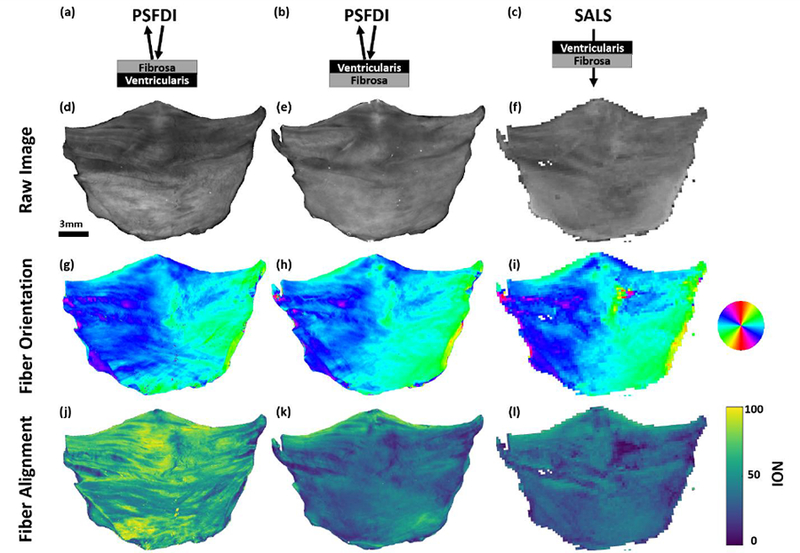
Ovine aortic valve leaflet imaging results. (a–c) Imaging geometry for the results in each column. (d–f) Raw intensity images for each technique. (g–i) Extracted fiber orientation, showing good agreement between each technique. (j–l) Extracted degree of fiber alignment from each technique. The pSFDI results show the ability to limit sampling depth to specific sides of the sample, while these results are obscured in the transmissive SALS technique. The results also indicate that the majority of the fiber alignment was present on the fibrosa side of the sample, which was expected.
Overall, pSFDI demonstrated sensitivity to differences in degree of fiber alignment between the leaflet layers, which the SALS system could not. Although similar features were evident in both the pSFDI alignment map on the ventricularis side (Figure 8k) and the SALS transmission alignment map (Figure 8l), the pSFDI alignment map showed a marked increase in NOI in the fibrosa.
Discussion
We present an extended analysis of polarized light reflectance from cylindrical scatterers that allows extraction of absolute degrees of fiber alignment, as quantified by the normalized orientation index (NOI), of collagen fibers in soft tissues. Our measurements of electrospun fiber samples with known fiber properties validated our model performance, with good agreement between modeled and measured optical anisotropy for our system. Additionally, the clear linear relationship between optical anisotropy (DOA) and structural anisotropy (NOI) provided the ability to extract absolute alignment information from our polarized light measurements. This relationship is valid for a large range of fiber sizes (rcyl = 50 – 1000 nm) and relative refractive indices (mrel = 1.02 – 1.12) that are relevant to both tissue and biomimetic tissue constructs. Therefore, the limited number of assumptions and only general a priori knowledge about the fibers in the sample allows direct comparison of the degree of fiber alignment between samples rather than only optical anisotropy.
While our inversion model is valid for a wide range of fiber properties, there are instances in which an NOI greater than 100 may be observed, as DOA has a theoretical maximum of 2. This high DOA may occur at large values of relative refractive index between the fiber and the medium (mrel > 1.2). However, in the case of hydrated collagen fibers in native, chemically unaltered tissues, such large relative refractive indices have not been reported to the author’s knowledge. This highlights the need for an appropriate inversion model to be used – for example, using the collagen fiber model to assess alignment in the electrospun fibers, which possess much higher refractive indices than collagen, would result in NOI values above 100. However, as our model incorporates a large range of relative refractive indices that are relevant to soft tissues, we do not expect to see measurements of greater than 100 when imaging heart valve tissues unless they have been chemically treated or dehydrated.
We also demonstrated the ability to rapidly capture high-resolution regional heterogeneity in heart valve leaflet tissue structure without any destructive sample preparation. There were clear differences in the pSFDI images of opposite sides of the leaflet, indicating the ability to distinguish distinct superficial layers of fiber structure on opposing sides of aortic heart valve leaflets which could not be captured using transmission-based techniques or techniques that have extended depth sampling into the sample. Most apparent were differences in degree of fiber alignment on the fibrosa and ventricularis sides of the leaflet tissue, confirming the increased presence of highly aligned collagen fibers in the fibrosa. However, as the ventricular thickness (~160 μm) is less than the sampling limitation (~250 μm) of the pSFDI system, it is likely that there is some signal from the underlying fibrosa layer. This could be avoided by use of higher spatial frequencies above 1 mm−1, at which sampling depth can be limited below 150 μm4. This improved pSFDI technique provides a powerful means for rapid, reflectance-based mapping of degree of collagen fiber alignment, with depth limitation for investigating superficial tissue layers without the need for chemical treatment or physical sectioning.
The pSFDI-derived NOI values were found to be higher than the NOI values extracted with SALS in the ovine aortic valve leaflet. We believe these differences may be due to two main factors. First, these techniques measure different phenomena of light transport in structured tissue. Additionally, as a transmissive technique, SALS measurements represent the degree of alignment through the entire thickness of the sample, while the reflective and depth-limited pSFDI, measurements are weighted by scattering events near the surface of the sample4, 47. Therefore, the populations of fibers sampled by each technique at similar lateral image locations may be different.
One deficiency of our light scattering model is that it does not account for the polarization response resultant from multiple-scattering from cylinders, which is a potential source of error between the model and experimental data. However, co-polarized imaging and sub-diffuse spatial frequency domain imaging both limit the number of scattering interactions that the system detects, such that the signal response is mainly representative of light undergoing few scattering events47. In addition to constraining the measurements to primarily back-scattering events by using high spatial frequencies, which follows the assumptions of our scattering model, the gating of reflectance to a small number of ballistic scattering events results in reduced sampling volumes, further refining the lateral and axial sampling volumes. However, although we modeled collagen fibers as infinitely long and straight cylinders, collagen fibers in unloaded valve tissues have been reported to possess a regular crimp with a period on the order of 10 μm28. In these cases, where the crimp period is shorter than the sampling resolution of a single pixel, the degree of fiber crimp will be included in the extracted NOI metric. Therefore, the extracted NOI metric should be understood to include both the alignment of multiple fibers as well as the individual fiber tortuosity within the sampling region for a given pixel. Additionally, it is assumed that single fiber families exist when interpreting the NOI metric. Interpretation of NOI in samples which are expected to have multiple fiber families with different primary orientations should be considered carefully – the extracted NOI may still be mathematically correct, but the corresponding interpretation of a unimodal PDF may be misleading.
In the current model, it is assumed that fibers are primarily aligned in the imaging plane. However, there are cases in which the longitudinal axis of the fibers are not entirely confined to the imaging plane. For example, fibers may have undulations or slight angular offsets from the imaging plane. The electrospun fibers exhibited small angular offsets from the imaging plane that were visible in the SEM images, and it is expected that the collagen fibers in the leaflet samples have similar small deviations from the imaging plane. However, the electrospun fiber experimental measurements and model results using this assumption were shown to have good agreement despite these small angular offsets from the imaging plane, though the errors of this assumption may have contributed to the discrepancies between the model and the experimental results. Therefore, we ignored minor deviations of the fiber orientation from the imaging plane in our analysis.
Alternatively, many native planar soft-tissues possess a 3-dimensional geometry and therefore are not confined to the 2-dimensional imaging plane, such as in the case of intact heart valves. In these cases, it is necessary to take into account the surface topography of the sample. It has previously been demonstrated that highly detailed surface topography can be extracted using phase-shifting profilometry50. The same patterns used for SFDI depth-limitation are also appropriate for extracting these height profiles using this phase shifting technique; this technique has already been used to improve optical property extraction from SFDI images of 3D samples20. Subsequently, we believe an extended model of off-axis light scattering from fibers or empirical calibration techniques could be used to correct for non-normal light incidence. Finally, it should be noted once more that the results of both of these cases are only considered valid for tissues in which the fibers are primarily aligned with the surface of the tissue. In cases where the fibers are primarily perpendicular to the sample surface, the presented modeling methods will likely not be suitable for assessing the fiber orientation or alignment, and would require substantial modification.
In future work, we plan to use pSFDI measurements to study collagen fiber structure in tissues undergoing stress- and strain-controlled biaxial mechanical testing. In addition to heart valve leaflets, other planar samples such as pericardium may be well-suited to study with pSFDI. Currently, the imaging rate of the system (about 0.2 Hz) requires imaging at discrete loading steps. However, imaging degree of collagen fiber alignment across tissue-level fields-of-view at discrete loading steps is still highly useful in understanding the mechanical behavior of tissues; in particular, we are interested in experimentally evaluating of the affine kinematic assumption. Additionally, the imaging rate may be improved further using hardware triggering of the camera, projector, and rotational stage. With the current hardware, an imaging rate of > 1 Hz is feasible; limitations at higher rates are primarily dependent on updating the projection pattern and data transfer rates between the camera and computer system.
Acknowledgements
This work was supported by funding from the National Heart, Lung, and Blood Institute of the National Institutes of Health (awards RO1-HL108330 & RO1-HL129077), the National Institute of Biomedical Imaging and Bioengineering of the National Institutes of Health (award T32-EB007505), and the Cancer Prevention & Research Institute of Texas (award RP-130702). The authors would also like to thank Mason Dana for his contributions to data collection and instrumentation troubleshooting, and acknowledge the Microscopy and Imaging Facility of the Institute for Cellular and Molecular Biology at The University of Texas at Austin for use of their electron microscope facilities. There are no conflicts of interest from financial or other commercial benefits related to the development of this manuscript.
Appendix A
The full derivation of our polarized light model begins from EQ4:
| (4) |
The initial Stokes vector describing the incident light , along with the Mueller matrix components representing the polarizer (Mp) and rotational transformations (Rp), are defined as follows:
| (A1) |
| (A2) |
| (A3) |
The Mueller matrix for the sample (Ms) is given as the special case scattering T-matrix derived for normally incident light scattering from infinitely long cylinders:
| (A4) |
The full solution for theT-matrix elements, along with efficient computational algorithms, has been described extensively by Bohren & Huffman5. The inputs required to solve for T11, T12, T33, and T34 are the relative refractive index of the cylinder and the medium (m), the size parameter (x), and the system collection angles (ψ). Plugging A1–A4 into EQ4 can be shown to simplify to:
| (A5) |
A5 shows that the intensity response detected by the camera is now entirely dependent on the linear polar response, and the Stokes vector can therefore be collapsed into EQ6.
Appendix B
To allow more rapid fitting, a modified but mathematically identical form of EQ6 is used. Each sinusoidal term includes a non-linear phase offset. For linearized fitting, it is transformed using the identity a·sin(θ)+b·cos(θ)=c·cos(θ+φ), where and φ=atan2(a, b). This results in a Fourier expansion form of EQ6:
| (A5) |
In this form, a linearized representation of the reflectance is I = Sb, where I is the detected reflectance intensity, S is the Fourier expansion representation of the model in A5, and b is a vector containing the five transformed model coefficients from A5. Solving this system of equations by b = S\I allows extraction of the coefficients by Gaussian elimination (Matlab function mldivide). Subsequently, a 1 second fitting time was achieved for a 1.5 – megapixel image, compared to several hours with the lsqnonlin fitting algorithms for the original equation containing a non-linear phase offset term. After fitting, the original form of the model coefficients and phase offset were recovered using the same identities.
References
- 1.Allen AC, Barone E, Cody O, Crosby K, Suggs LJ and Zoldan J. Electrospun poly (N-isopropyl acrylamide)/poly (caprolactone) fibers for the generation of anisotropic cell sheets. Biomaterials science 5: 1661–1669, 2017. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 2.Amoroso NJ, D’Amore A, Hong Y, Wagner WR and Sacks MS. Elastomeric electrospun polyurethane scaffolds: the interrelationship between fabrication conditions, fiber topology, and mechanical properties. Advanced Materials 23: 106–111, 2011. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 3.Ayoub S, Tsai KC, Khalighi AH and Sacks MS. The Three-Dimensional Microenvironment of the Mitral Valve: Insights into the Effects of Physiological Loads. Cellular and Molecular Bioengineering 11: 291–306, 2018. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 4.Bodenschatz N, Krauter P, Liemert A, Wiest J and Kienle A. Model-based analysis on the influence of spatial frequency selection in spatial frequency domain imaging. Applied optics 54: 6725–6731, 2015. [DOI] [PubMed] [Google Scholar]
- 5.Bohren CF and Huffman DR. Absorption and scattering of light by small particles. John Wiley & Sons, 2008. [Google Scholar]
- 6.Chenault DB and Chipman RA. Measurements of linear diattenuation and linear retardance spectra with a rotating sample spectropolarimeter. Applied optics 32: 3513–3519, 1993. [DOI] [PubMed] [Google Scholar]
- 7.Courtney T, Sacks MS, Stankus J, Guan J and Wagner WR. Design and analysis of tissue engineering scaffolds that mimic soft tissue mechanical anisotropy. Biomaterials 27: 3631–3638, 2006. [DOI] [PubMed] [Google Scholar]
- 8.Cuccia DJ, Bevilacqua F, Durkin AJ, Ayers FR and Tromberg BJ. Quantitation and mapping of tissue optical properties using modulated imaging. J Biomed Opt 14: 024012–024012–024013, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 9.Cuccia DJ, Bevilacqua F, Durkin AJ and Tromberg BJ. Depth-sectioned imaging and quantitative analysis in turbid media using spatially modulated illumination In: Biomedical Topical Meeting Optical Society of America, 2004, p. FF5. [Google Scholar]
- 10.Cuccia DJ, Bevilacqua F, Durkin AJ and Tromberg BJ. Modulated imaging: quantitative analysis and tomography of turbid media in the spatial-frequency domain. Opt. Lett 30: 1354–1356, 2005. [DOI] [PubMed] [Google Scholar]
- 11.D’Amore A, Stella JA, Wagner WR and Sacks MS. Characterization of the complete fiber network topology of planar fibrous tissues and scaffolds. Biomaterials 31: 5345–5354, 2010. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 12.Deitzel J, Kleinmeyer J, Harris D and Tan NB. The effect of processing variables on the morphology of electrospun nanofibers and textiles. Polymer 42: 261–272, 2001. [Google Scholar]
- 13.Doshi J and Reneker DH. Electrospinning process and applications of electrospun fibers. In: Industry Applications Society Annual Meeting, 1993., Conference Record of the 1993 IEEEIEEE, 1993, p. 1698–1703. [Google Scholar]
- 14.Eckert CE, Fan R, Mikulis B, Barron M, Carruthers CA, Friebe VM, Vyavahare NR and Sacks MS. On the biomechanical role of glycosaminoglycans in the aortic heart valve leaflet. Acta biomaterialia 9: 4653–4660, 2013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 15.Fratzl P Collagen: structure and mechanics, an introduction In: Collagen Springer, 2008, pp. 1–13. [Google Scholar]
- 16.Gelse K, Pöschl E and Aigner T. Collagens—structure, function, and biosynthesis. Advanced drug delivery reviews 55: 1531–1546, 2003. [DOI] [PubMed] [Google Scholar]
- 17.Ghosh N and Vitkin IA. Tissue polarimetry: concepts, challenges, applications, and outlook. J Biomed Opt 16: 110801–11080129, 2011. [DOI] [PubMed] [Google Scholar]
- 18.Ghosh N, Vitkin IA and Wood MF. Mueller matrix decomposition for extraction of individual polarization parameters from complex turbid media exhibiting multiple scattering, optical activity, and linear birefringence. J Biomed Opt 13: 044036–044036–044014, 2008. [DOI] [PubMed] [Google Scholar]
- 19.Gilbert TW, Wognum S, Joyce EM, Freytes DO, Sacks MS and Badylak SF. Collagen fiber alignment and biaxial mechanical behavior of porcine urinary bladder derived extracellular matrix. Biomaterials 29: 4775–4782, 2008. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 20.Gioux S, Mazhar A, Cuccia DJ, Durkin AJ, Tromberg BJ and Frangioni JV. Three-dimensional surface profile intensity correction for spatially modulated imaging. J Biomed Opt 14: 034045, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 21.Goth W, Lesicko J, Sacks MS and Tunnell JW. Optical-Based Analysis of Soft Tissue Structures. Annu Rev Biomed Eng 18: null, 2016. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 22.Guo X, Wood MF and Vitkin A. A Monte Carlo study of penetration depth and sampling volume of polarized light in turbid media. Optics Communications 281: 380–387, 2008. [Google Scholar]
- 23.Holzapfel GA Biomechanics of soft tissue. The handbook of materials behavior models 3: 1049–1063, 2001. [Google Scholar]
- 24.Hotaling NA, Bharti K, Kriel H and Simon CG. DiameterJ: a validated open source nanofiber diameter measurement tool. Biomaterials 61: 327–338, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 25.Hulst HC and Van De Hulst H. Light scattering by small particles. Courier Dover Publications, 1957. [Google Scholar]
- 26.Jacques SL and Ramella-Roman JC. Polarized light imaging of tissues. Royal Society of Chemistry, 2004, p. 591–607. [Google Scholar]
- 27.Jammalamadaka SR and Sengupta A. Topics in circular statistics. world scientific, 2001. [Google Scholar]
- 28.Joyce EM, Liao J, Schoen FJ, Mayer JE Jr and Sacks MS. Functional collagen fiber architecture of the pulmonary heart valve cusp. The Annals of thoracic surgery 87: 1240–1249, 2009. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 29.Kemp N, Zaatari H, Park J, Rylander III HG and Milner T. Form-biattenuance in fibrous tissues measured with polarization-sensitive optical coherence tomography (PS-OCT). Optics Express 13: 4611–4628, 2005. [DOI] [PubMed] [Google Scholar]
- 30.Liu B, Harman M, Giattina S, Stamper DL, Demakis C, Chilek M, Raby S and Brezinski ME. Characterizing of tissue microstructure with single-detector polarization-sensitive optical coherence tomography. Applied optics 45: 4464–4479, 2006. [DOI] [PubMed] [Google Scholar]
- 31.Lu S-Y and Chipman RA. Interpretation of Mueller matrices based on polar decomposition. JOSA A 13: 1106–1113, 1996. [Google Scholar]
- 32.Mark JE Physical properties of polymers handbook. Springer, 2007. [Google Scholar]
- 33.Martin C and Sun W. Biomechanical characterization of aortic valve tissue in humans and common animal models. Journal of biomedical materials research Part A 100: 1591–1599, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 34.Mega Y, Robitaille M, Zareian R, McLean J, Ruberti J and DiMarzio C. Quantification of lamellar orientation in corneal collagen using second harmonic generation images. Optics Letters 37: 3312–3314, 2012. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 35.Misfeld M and Sievers H-H. Heart valve macro-and microstructure. Philosophical Transactions of the Royal Society of London B: Biological Sciences 362: 1421–1436, 2007. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 36.Oppenheim AV and Schafer RW. Discrete-time Signal Processing. Prentice Hall, 1989, pp. 87–86. [Google Scholar]
- 37.Parry DA The molecular fibrillar structure of collagen and its relationship to the mechanical properties of connective tissue. Biophysical chemistry 29: 195–209, 1988. [DOI] [PubMed] [Google Scholar]
- 38.Qi J and Elson DS. Mueller polarimetric imaging for surgical and diagnostic applications: a review. Journal of biophotonics 10: 950–982, 2017. [DOI] [PubMed] [Google Scholar]
- 39.Sacks MS Incorporation of experimentally-derived fiber orientation into a structural constitutive model for planar collagenous tissues. Journal of biomechanical engineering 125: 280–287, 2003. [DOI] [PubMed] [Google Scholar]
- 40.Sacks MS, Smith DB and Hiester ED. A small angle light scattering device for planar connective tissue microstructural analysis. Annals of biomedical engineering 25: 678–689, 1997. [DOI] [PubMed] [Google Scholar]
- 41.Samuels RJ Small angle light scattering from deformed spherulites. Theory and its experimental verification In: Journal of Polymer Science Part C: Polymer Symposia Wiley Online Library, 1966, p. 37–53. [Google Scholar]
- 42.Stella JA and Sacks MS. On the biaxial mechanical properties of the layers of the aortic valve leaflet. Journal of biomechanical engineering 129: 757–766, 2007. [DOI] [PubMed] [Google Scholar]
- 43.Stoller P, Reiser KM, Celliers PM and Rubenchik AM. Polarization-modulated second harmonic generation in collagen. Biophysical journal 82: 3330–3342, 2002. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 44.Sun M, He H, Zeng N, Du E, Guo Y, Liu S, Wu J, He Y and Ma H. Characterizing the microstructures of biological tissues using Mueller matrix and transformed polarization parameters. Biomedical optics express 5: 4223–4234, 2014. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 45.Tower TT, Neidert MR and Tranquillo RT. Fiber alignment imaging during mechanical testing of soft tissues. Annals of biomedical engineering 30: 1221–1233, 2002. [DOI] [PubMed] [Google Scholar]
- 46.Van Krevelen DW and Te Nijenhuis K. Properties of polymers: their correlation with chemical structure; their numerical estimation and prediction from additive group contributions. Elsevier, 2009. [Google Scholar]
- 47.Wiest J, Bodenschatz N, Brandes A, Liemert A and Kienle A. Polarization influence on reflectance measurements in the spatial frequency domain. Physics in medicine and biology 60: 5717, 2015. [DOI] [PubMed] [Google Scholar]
- 48.Yang B, Lesicko J, Sharma M, Hill M, Sacks MS and Tunnell JW. Polarized light spatial frequency domain imaging for non-destructive quantification of soft tissue fibrous structures. Biomedical optics express 6: 1520–1533, 2015. [DOI] [PMC free article] [PubMed] [Google Scholar]
- 49.York T, Kahan L, Lake SP and Gruev V. Real-time high-resolution measurement of collagen alignment in dynamically loaded soft tissue. J Biomed Opt 19: 066011, 2014. [DOI] [PubMed] [Google Scholar]
- 50.Zhou W-S and Su X-Y. A direct mapping algorithm for phase-measuring profilometry. Journal of Modern Optics 41: 89–94, 1994. [Google Scholar]


