Occupancy Modeling Species-Environment Relationships with Non-ignorable Survey Designs

Abstract

Statistical models supporting inferences about species occurrence patterns in relation to environmental gradients are fundamental to ecology and conservation biology. A common implicit assumption is that the sampling design is ignorable and does not need to be formally accounted for in analyses. The analyst assumes data are representative of the desired population and statistical modeling proceeds. However, if datasets from probability and non-probability surveys are combined or unequal selection probabilities are used, the design may be non-ignorable. We outline the use of pseudo-maximum likelihood estimation for site-occupancy models to account for such non-ignorable survey designs. This estimation method accounts for the survey design by properly weighting the pseudo-likelihood equation. In our empirical example, legacy and newer randomly selected locations were surveyed for bats to bridge a historic statewide effort with an ongoing nationwide program. We provide a worked example using bat acoustic detection/non-detection data and show how analysts can diagnose whether their design is ignorable. Using simulations we assessed whether our approach is viable for modeling datasets composed of sites contributed outside of a probability design.

Pseudo-maximum likelihood estimates differed from the usual maximum likelihood occupancy estimates for some bat species. Using simulations we show the maximum likelihood estimator of species-environment relationships with non-ignorable sampling designs was biased, whereas the pseudo-likelihood estimator was design-unbiased. However, in our simulation study the designs composed of a large proportion of legacy or non-probability sites resulted in estimation issues for standard errors. These issues were likely a result of highly variable weights confounded by small sample sizes (5% or 10% sampling intensity and 4 revisits). Aggregating datasets from multiple sources logically supports larger sample sizes and potentially increases spatial extents for statistical inferences. Our results suggest that ignoring the mechanism for how locations were selected for data collection (e.g., the sampling design) could result in erroneous model-based conclusions. Therefore, in order to ensure robust and defensible recommendations for evidence-based conservation decision-making, the survey design information in addition to the data themselves must be available for analysts. Details for constructing the weights used in estimation and code for implementation are provided.

Introduction

Statistical analyses that explore species occurrence patterns in relation to habitat, climate, or anthropogenic disturbance are fundamental to ecology and conservation biology and rely on model-based inferences. A model (or set of models) is formulated to provide an approximation of the ecological process generating observed patterns in the data. The fact that statistical models are an abstraction of reality is well known (Box 1976). An under-appreciated and implicit assumption in these model-based analyses is that the survey design is ignorable (Pfeffermann 1993; Winship & Radbill 1994). Statistically, an ignorable design meets the condition that probability of sample unit i being selected in the sample S, Pr(i in S) = π_i or inclusion probability, is independent of the response variable conditional on explanatory variables (Pfeffermann 1993). It is not unusual for analysts to ignore their sampling design and assume that how sample units (or analysis units) were selected in space or time does not impact parameter estimates of species-environment relationships. However, we show that assuming ignorability could be a faulty approach, particularly if data from probability and non-probability designs are combined for statistical analyses or sample units are selected with unequal probabilities.

The potential impacts of site-selection bias on model-based inference has been widely reported among statisticians (for discussion see Gelman 2007, and references therein). But only recently was geographic bias, a form of site-selection bias, acknowledged when using presence-only species distribution models in ecology (e.g., Dorazio 2014, although see Conn et al. 2017 for abundance data). This problem has not otherwise been addressed in ecology but may be broadly relevant given increasing use of complex and unequal probability survey designs (e.g., Stevens Jr & Olsen 2004; Theobald et al. 2007, cited 388 and 64 times web of science v.5.24 June 20, 2017, respectively). A complex or unequal probability design may arise when combining historic survey locations with newer locations or aggregating datasets from different projects or programs. Here, we explore approaches for properly estimating species-environment relationships using an occupancy model when the survey design is non-ignorable.

In the case of informative (or non-ignorable) sampling, one option is to incorporate additional covariates and/or model structure that characterizes the survey design. For instance, with stratified or cluster probability sampling including indicators for each strata or random effects for each primary sampling unit (or group) will control for the design in model-based analyses (Section 3.6 and 5.6 Lohr 2010). Those are relatively simple cases. For complex probability sampling, such as selecting relative to predicted species abundance (e.g., Ringvall & Kruys 2005) or based on a GIS accessibility surface (e.g., Theobald et al. 2007), identifying how to account for the design within a statistical model becomes challenging. Some of these difficulties are: 1) additional design variables to include are not known or unavailable, 2) modeling interactions between the design variables and explanatory variables of ecological interest are challenging, and 3) as the number of interactions increases, the likelihood of low sample sizes or no data for certain combinations increases (Pfeffermann 2007). Another option is to jointly model the observed response variable and the process governing the selection of the observed set of sample units (Diggle et al. 2010; Si et al. 2015; Conn et al. 2017). However, constructing a properly specified joint model is difficult and adds analytical complexity. We present a simpler approach, pseudo-maximum likelihood estimation (P-MLE), that accounts for the complex survey design by properly weighting the log-likelihood equation.

An example of a complex survey design is the one proposed for an omnibus North American continent-wide bat monitoring program (called “NABat,” Loeb et al. 2015). North American bats are facing increasingly serious conservation threats due to rapid spread of the bat disease white-nose syndrome, expanding footprint of the wind power industry, and accelerated global change (O’Shea et al. 2016). NABat proposes a “master sample” to facilitate collaboration and data-sharing among partners (Larsen et al. 2008). This approach allows different organizations to define their own spatial domain of interest and level of survey effort within a common probabilistic framework. However, this flexibility results in an unequal probability sample when the partner contributed datasets are combined into a comprehensive analysis (Fig. 1). Additional complexity arises if data are included from sample units selected purposively (or non-probabilistically) because they were surveyed by previously established programs or opportunistically due to convenience or proximity to pre-existing operations. If the final set of sample units are not representative of the meaningful environmental gradients influencing bat distribution and abundance across a given spatial domain, (e.g., forest cover, Rodhouse et al. 2015), the complex survey design could be non-ignorable depending on the fitted model.

Fig. 1.

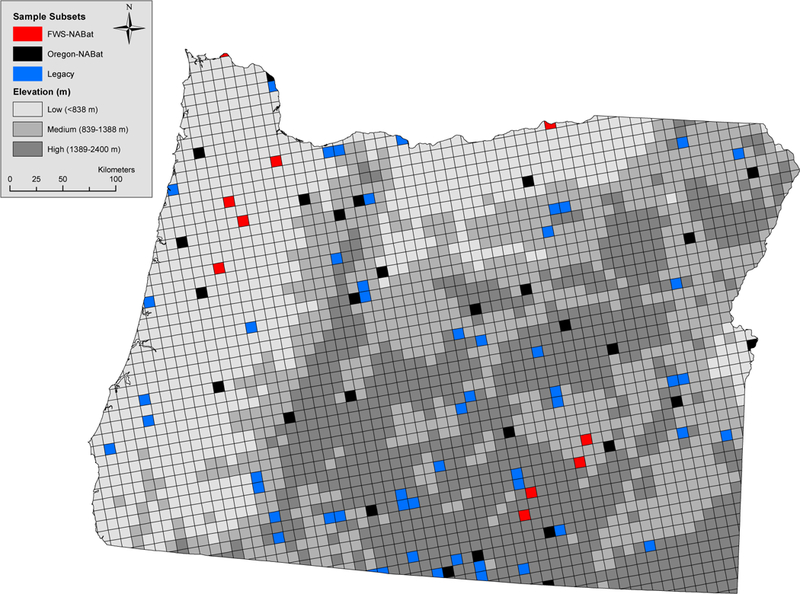
An example of a complex survey design that was used for Oregon acoustic bat surveys in 2016. Fifty-three legacy sites selected purposively, 10 selected using the Region 1 Fish and Wildlife Service portion of the NABat master sample, and 28 selected using the Oregon subset of the NABat master sample. Gray-scale shading depicts the three elevational groups (strata) created for simulation demonstration presented in Appendix S2.

For a thorough worked example, we analyze detection/non-detection data for three bat species observed in Oregon, USA during 2016 using single-season site-occupancy models that account for imperfect detection (MacKenzie et al. 2006). The sampling design for Oregon exemplifies a complex survey design likely to arise in ecological applications, a combination of an unequal probability sample resulting from a master sample and purposively selected sites based on a legacy program (Fig. 1). We compare the P-ML to the traditional maximum likelihood (ML) estimates that assume the complex design employed in Oregon is ignorable. Our P-MLE code for site-occupancy models is included as Data S1. Using simulations, we explore whether the P-ML approach is a viable alternative to model datasets composed of sites contributed outside the probability design. We supply the simulation code for researchers to explore their own design specifications and parameter values in Data S2. Further, we verify that P-ML site-occupancy model estimates are design unbiased for unequal probability designs in Appendix S2. We discuss practical guidance and present simple diagnostics for assessing whether a survey design is ignorable within an occupancy modeling framework.

Methods

In this section, we introduce pseudo-likelihood estimation for occupancy modeling data collected following a probabilistic sampling design. Occupancy models allow for estimating species occurrence relationships with environmental variables while accounting for imperfect detection (MacKenzie et al. 2006). To provide context for the approach, we begin by introducing a specific example of a complex survey design for bats. Then we show one option for calculating the realized sample weights based on a survey design composed of probability and non-probability samples. We provide the details on how to incorporate sample weights in the log-likelihood (i.e., pseudo-likelihood) for estimating occupancy model parameters. Finally, we outline our simulation study that explores whether our proposed method for occupancy modeling datasets composed of sites contributed outside a probability design is reasonable.

Empirical example of a complex survey design

An Oregon statewide interagency collaborative effort to acoustically survey bats was launched to inform spatially explicit species occupancy models (see Rodhouse et al. 2012; Rodhouse et al. 2015). Previous analyses were based on bat data collected by a program active during 2003–2010 (Rodhouse et al. 2012). To ensure compatibility with the NABat program while also maintaining consistency with the historic program, a “hybrid” design was created for 2016 acoustic bat surveys in Oregon (as suggested by adaptive monitoring strategies, sensu Lindenmayer & Likens 2009). Both programs used the same areal grid-based sample frame composed of 10-km x 10-km grid cells or sample units covering the contiguous United States (hereafter, CONUS; Rodhouse et al. 2012; Loeb et al. 2015, Fig. 1). The main distinction between the legacy and new program was the mechanism proposed for selecting sample units to survey— a purposive sample versus probabilistic master sample.

The collection of sample units with data available for an analysis was comprised of three groups: a set of legacy sample units and two unique spatial subsets from the NABat master sample (Fig. 1). The fifty-three legacy sample units were included because they were previously surveyed during 2003–2010 (referred to as “Legacy” sample units). Legacy sites had been selected purposively to distribute effort in a representative manner across Oregon and Washington and to ensure inclusion of forest and shrub-steppe habitats (Rodhouse et al. 2012). On the other hand, the NABat master sample was a probabilistic design created by applying the generalized random tessellation stratified (GRTS) algorithm to randomly order all sample units in the CONUS areal frame (Stevens Jr & Olsen 2004; Loeb et al. 2015; Kincaid et al. 2016). The NABat master sample was a spatially balanced ordered list of all the 10-km x 10-km grid cells and any consecutively numbered subset should be spatially balanced. In our example, the Oregon state boundary defined one sub-domain of interest within the master sample (i.e., geographic subset Larsen et al. 2008). Twenty-eight grid cells were selected based on following GRTS order within this Oregon subset (referred to as “Oregon NABat”). The US Fish and Wildlife Service in Region 1 independently conducted acoustic surveys in 30 grid cells following the NABat plan and used the geographic subset defined by intersecting refuge boundaries within Oregon, Washington, Idaho, and Nevada with the NABat master sample, but off-shore refuges were excluded (referred to as “FWS NABat”, pers. communication Jenny Barnett). For our analyses, 10 of the 30 FWS NABat sample units were within Oregon, resulting in a total statewide sample size of 91 (denoted n = 91) for occupancy modeling (Fig. 1).

We explored acoustic records (echolocation calls) for three bat species: silver-haired bat (LANO; Lasionycteris noctivagans), little brown myotis (MYLU; Myotis lucifugus), and long-legged myotis (MYVO; Myotis volans). To estimate detectability within a site-occupancy model, up to four acoustic detectors were dispersed within a grid cell for recording during the same night. These were considered independent spatial replicates within a 10-km x 10-km sample unit (grid cell). This decision was based on Wright et al. (2016) that found spatial replicates were more likely to be independent than when detectors were deployed at the same location for consecutive nights. For the purposes of this analysis, we used only human-verified evidence of a species detection at each acoustic detector for a given night, supporting our simplifying assumption that no false positive errors were made.

Estimation of site-occupancy models with informative survey designs

The use of sample weights or inclusion probabilities are fundamental to design-based analyses that, typically, focus on estimating a finite population quantity, such as a population total or mean. The associated uncertainty with a design-based estimate is directly related to the probabilistic selection of a sample from a finite population (randomization theory). We are interested in estimating an occupancy model that characterizes species occurrence associations with habitat or environmental gradients (e.g., elevation and forest cover) within a defined spatial extent (e.g., Oregon). The inferential goal is to estimate the parameters that describe the data generating process, sometimes referred to as superpopulation modeling (Sarndal et al. 1992). The observed value for each sample unit in the finite population is considered one stochastic realization from the superpopulation model. Our model-based estimation incorporates survey design information in the form of sample weights similar to a design-based analysis.

One approach to calculating realized sample weights

Incorporating sample weights into the estimation procedure for ecological parameters of interest can adjust for the potential design bias induced by the mechanism used to select which sample units were surveyed. However, proper calculation of sample weights requires tracking survey design information which is an unfamiliar aspect of data management for ecological analyses. In order to employ the pseudo-likelihood approach for estimating model-based parameters, the realized sample weights need to be calculable for a given dataset. The sample weight (denoted as w_i) is interpreted as the number of units in the finite population represented by unit i (Lohr 2010). This could be estimated by inverting the inclusion probabilities $(w_{\text{i}}={\pi }_{\text{i}}^{-1})$ for common probability designs (e.g., simple random or stratified random). Additionally, the sample weights could be adjusted for non-response errors such as when sites were not surveyed because of accessibility or safety concerns (Lesser & Kalsbeek 1999; Munoz & Lesser 2006). However, note that non-response errors are different than detection errors, a common measurement error that occurs with wildlife studies. Detection errors are false zeros, a species is not recorded because an observer didn’t see or “detect” it within a plot. In our example, this occurs when a bat species was available in the grid cell but all the detectors did not record at least one high quality call that could be human verified to a species.

Master sample designs can result in variable sampling intensity among different projects or partners and this effort is not necessarily controlled or known at the outset of its use. Similar to post-stratification (Chapter 4 Lohr 2010), the realized sample weights for a master sample design can be found by defining the unique geographic subsets that are represented in the final dataset (Larsen et al. 2008). In our example, we define three unique geographic subsets (h = {1, 2 or 3}) that partition the total number of sample units or grid cells available in Oregon (N = 2660). One subset included sample units that were located on US Fish and Wildlife Service Region 1 refuges within the state of Oregon and 212 grid cells met this condition (FWS NABat, Table 1). Another subset corresponded to 2395 sample units within the state of Oregon not on US Fish and Wildlife Service Region 1 refuges and not included in the legacy program (Oregon NABat, Table 1). To integrate the non-probability or legacy sites, we take a conservative approach (e.g., Cox & Piegorsch 1996) and define a third strata composed only of the 53 legacy sample units (Table 1). Then the sample weights are calculated as for a stratified design with w_i in h = N_h/n_h for all units i that are a member of strata or subset h, where N_h is the total number of sample units in strata or subset h and n_h is the number of sample units surveyed in strata or subset h. In our case, Oregon NABat sites all have weights of 2395/28 = 85.54, FWS NABat weights are all 212/10 = 21.2, and legacy sites all have a weight of 1. A weight of 1 assumes legacy sites only represent themselves in the population of interest (i.e., Oregon). This is conservative and adjusting the weights higher based on the environmental space sampled by the legacy locations could be considered in other applications (Overton et al. 1993; Maas-Heber et al. 2015), similar to propensity score adjustments for non-response errors (Munoz & Lesser 2006).

Table 1.

Combined survey design information for Oregon acoustic bat surveys in 2016, where n_h represents the number of sample units in unique subset or strata h, N_h is the total number of units within that unique subset h, w_{i in h} is the original sample weight for unit i in subset h, and ${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}h}$ is the adjusted weight for unit i in subset h.

	Oregon NABat	FWS NABat	Legacy
nh	28	10	53
Nh	2395	212	53
wi in h = Nh/nh for all i in h	85.54	21.2	1
${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}h}$ for all i in h	2.93	0.73	0.03

An issue when incorporating sample weights in a likelihood-based analysis of complex survey data is determining how to scale the weights to reduce bias and improve precision of estimators (e.g., Rabe-Hesketh & Skrondal 2006; Kim & Skinner 2013). Here we explored a relatively simple approach such that the sum over all adjusted weights is the sample size (n = 91), otherwise the sum of the non-adjusted weights would be the finite population size (N = 2660). The result of adjusting the weights was that interval estimation was unbiased (similar to Equation 12.13 in Pfefferman & Sverchkov 2003). Following Savitsky et al. (2015) we calculate ${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}h}=\left(N_h/n_h\right)\left(1/\overline{w}\right)$ where $\overline{w}={\sum }_h{\sum }_i{w}_i\hspace{0.33em}\text{in}\hspace{0.33em}h/n={\sum }_h{N}_h/n=N/n$ is the average sample weight (Table 1). Then the adjusted weights ${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}h}$ are (N_h/n_h)(1/w) and ${\sum }_h{\sum }_i{\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}h}=n$. The adjusted weights for our example become ${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}\text{Oregon}\hspace{0.33em}\text{NABat}}=2.93$, ${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}\text{FWS}\hspace{0.33em}\text{NABat}}=0.73$ and ${\tilde{w}}_{i\hspace{0.33em}\text{in}\hspace{0.33em}\text{Legacy}}=0.03$.

Pseudo-likelihood Approach

An estimating equation approach, as proposed for generalized linear models, accounts for the potential discrepancy between the sample and census likelihood (Pfefferman & Sverchkov 2003; Kim & Skinner 2013; Brown & Olsen 2013). The census likelihood assumes all $N=(={\sum }_h{N}_h=2660)$ grid cells were surveyed. Let n be the actual number of sample units or grid cells (i = 1, · · · , n) surveyed $({\sum }_h{n}_h=n=91)$ out of the total number of sample units in the sample frame, K_i equal the number of revisits per site (in our case the number of detectors deployed on a night per sample unit i), and y_ik is a 1 if the species was detected on the k^th survey within the i^th sample unit. The I(D_i) is an indicator variable for whether sampling unit i had no detections for any detector (I(D_i) = 1, otherwise I(D_i) = 0). The census likelihood for an occupancy model assuming constant detection (p) and heterogeneity in occupancy (ψ_i) follows

$$L({\psi }_i,p|\text{y})=\prod _{i=1}^N\left({\psi }_i\left(\prod _{k=1}^{K_i}{p}^{y_{ik}}{(1-p)}^{1-y_{ik}}\right)+(1-{\psi }_i)I(D_i)\right),$$ (1)

where ψ_i = exp(Xβ) ∗ (1 + exp(Xβ))⁻¹ allows for occupancy-level covariates (X) and β are the parameters of interest that represent species-environment relationships for model-based inferences.

The sample likelihood is the product over n sample units, as opposed to N , and on the log-arithmic scale the equation is the sum of n log-likelihood contributions. A proposed estimator with an informative design is to adjust the log of the likelihood contribution from the i^th unit by multiplying it by its respective sample weight, w_i:

$$\log L(\psi ,p|\text{y},\text{w})=\sum _{i=1}^n{w}_i\ast log\left({\psi }_i\left(\prod _{k=1}^{K_i}{p}^{y_{ik}}{(1-p)}^{1-y_{ik}}\right)+(1-{\psi }_i)I(D_i)\right).$$ (2)

The formal derivation of this equation was presented as Equation 12.15 in Pfefferman & Sverchkov (2003) and is related to the Horvitz-Thompson estimator for the score equations (see Appendix S1). Note that if the survey design is a simple random sample then the sample weights are all equal (w_i = N/n) and the log-likelihood is the same as presented by MacKenzie et al. (2006). The maximum likelihood estimates are the solutions to the score equations— the set of first partial derivatives of the log-likelihood (Pawitan 2001). We used the adjusted weights (e.g., $\tilde{w}$ from Table 1) in the likelihood to achieve unbiased interval estimation (Equation 12.13 in Pfefferman & Sverchkov 2003). Otherwise the standard errors are too small because the negative second partial derivative of the log-likelihood evaluated at the maximum is as if all N sample units were surveyed and not a sample of size n. Solutions were found in R (R Core Team 2016) using the optim function for parameters on the logit-scale. We refer to this as the pseudo-maximum likelihood estimator (P-MLE). Standard errors were based on the square roots of diagonal elements from the inverse of the Hessian matrix output from optim. Then the 95% confidence interval (CI) is the point estimate plus or minus 1.96 times the associated standard error.

A suggested diagnostic for assessing whether a design is ignorable is to compare the P-MLE to MLE for a given fitted model (e.g., Bollen et al. 2016). We provide more mathematical details in Appendix S1 motivating the use of this diagnostic for testing whether a design is informative given a fitted model. We also discuss other visualization-based options in Appendix S1. To show an empirical example of this approach, we estimated detection probabilities and occupancy parameters using P-MLE and MLE (w_i = 1 for all i in Equation 2) for the combined dataset composed of the probability and non-probability selected sites in Oregon. Mean elevation and percent forest cover for each sample unit were included as occupancy-level co-variates for LANO, MYLU, and MYVO based on previous species distribution models for these species (Rodhouse et al. 2015), while detection was assumed constant. We provide our code for estimating single-season site-occupancy models using P-ML or ML in Data S1.

Simulation study

We demonstrate that using P-MLE for analyzing an unequal probability design arising from a master sample adjusts for potential design bias in occupancy and detection parameters as expected (Appendix S2). Here we focus on whether our conservative approach of assigning a sample weight of 1 to each legacy site is appropriate for a dataset composed of probability and non-probability selected units. To create a simulated finite population, we generated the latent occupancy state (Z_i) for every sample unit i = 1, · · · , 2660 as a Bernoulli(ψ_i) random variable with logit(ψ_i) = β₀ + β₁elevation_i + β₂forest_i and β₀ = 1.5, β₁ = 1, β₂ = 2. The forest and elevation (mean) covariates were the actual values available for the entire state of Oregon (2660 10-km x 10-km sample units). We simulated detection histories with K_i = 4 or 8 independent revisits for each site i, conditional on occupancy (Z_i = 1), as Bernoulli(p) random variables with detection probability (p) equal to 0.5 for all revisits.

Then each of 1000 simulated finite populations (N = 2660) were sampled following a hybrid sampling design similar to the Oregon example composed of probability selected sites (SRS) and non-probability sites (Legacy). A purposive sample of grid cells with the largest values of both elevation and forest (hence highest probability of occupancy from the generating model) were selected as legacy sites. Sampling intensities of 5%, 10%, 20% were used and for each sample size the proportion of legacy sites was altered (75%, 50%, or 25%) (Table 2). The adjusted weights calculated as described for the combined Oregon survey are shown in Table 2.

Table 2.

Hybrid designs with sites selected using a simple random sample (probability) and legacy (non-probability). Legacy sites contributed varying percentages to the total sample size. Legacy sites chosen based on different distances from the maximum point within euclidean space of elevation and % forest in Oregon, mimicking a very purposive sampling design that could be based on known bat occurrence patterns. In the results column, we denote an X for those combinations that produced similar results as those shown in Fig. 3, a for scenarios with computational issues, and a o for scenarios with larger uncertainty compared to the results shown in Fig. 3. Other scenarios can be investigated using Data S2.

Sampling Intensity (n)	Relative % Contribution		Adjusted Sample Weights		Results
	Probability	Legacy	Probability	Legacy	4 revisits	8 revisits
5% (139)	75%	25%	1.32	0.05	o	o
	50%	50%	1.96	0.05	∗	o
	25%	75%	3.82	0.05	∗	∗
10% (278)	75%	25%	1.30	0.10	X	X
	50%	50%	1.90	0.10	X	X
	25%	75%	3.71	0.10	∗	X
20% (555)	75%	25%	1.26	0.21	X	X
	50%	50%	1.79	0.21	X	X
	25%	75%	3.37	0.21	X	X

A total of 9 × 1000 simulated datasets resulted from sampling each simulated finite population under the hybrid design with different sample sizes and percent contributions from purposively selected legacy sites. For each simulated dataset, four different mean structures for ψ were assumed: (1) the data generating model with both elevation and percent forest explanatory variables (denoted, Elev.+For.); (2) a model with only percent forest (denoted, For.); (3) a model with only elevation (denoted, Elev.); and (4) an intercept only model assuming no heterogeneity in site-occupancy (denoted, Int.). Detection (p) was assumed constant for all models. The four models were estimated using P-MLE (Equation 2 with adjusted weights from Table 2) and MLE (the design is ignored, w_i = 1 for every sample unit i). The hybrid designs were likely non-ignorable for all fitted models, except perhaps when specifying the data generating model (again for empirical datasets this model is unknown).

For a given design D and fitted model (denoted M_k), variation in the parameter estimates ${\widehat{\beta }}_{D|M_k}$ across the simulated datasets was a combination of estimation error + sampling error. Estimation error is the discrepancy of model estimates based on one realization of data from their corresponding true values. In simulations, the observed variation among model estimates arises from fitting a given model to different realizations of data. Sampling error, on the other hand, is the discrepancy of estimated sample-based quantities from their corresponding value based on a finite population. The realization of data values for the finite population are considered fixed. If the entire population were surveyed (a census), there would be no sampling error. However, in our empirical bat data, even if the entire finite grid was censused, there is still observation error because of imperfect detection and process error related to specifying the species-environment relationships.

To isolate the impacts of sampling error for a given model (M_k), we compared estimates $({\widehat{\beta }}_{D|M_k})$ to fitting the same model but assuming a census was conducted (N = n = 2660), ${\widehat{\beta }}_{census|M_k}$ based on maximizing Equation 1. The average census values $({\widehat{\beta }}_{census|M_k})$ will differ from the data-generating values (β_truth|M_truth) due to fitting a different model (M_k) than the data-generating model (M_truth) for the species-environment relationships (essentially, model misspecification). In our study, the average census estimates varied among the fitted models because of our assumed data generating values and because elevation and percent forest were slightly correlated. Also, we compared the estimates for a given design and model $({\widehat{\beta }}_{D|M_k})$ to the data generating values, β_truth|M_truth . On average the estimates will differ from the data generating values depending on the design (D) used to select sample units and the assumed model (M_k) for the species-environment relationships, ideally we want this difference to be close to zero (or unbiased). For each sampling design and fitted model, average 95% Cis (averages of the upper and lower bounds) and average of the point estimates $({\widehat{\beta }}_{D|M_k})$ were calculated across all simulated datasets as a summary. We also examined two different coverage properties. Coverage is the proportion of 95% CIs that contained the corresponding census value ${\widehat{\beta }}_{census|M_k}$ assuming all grid cells were surveyed in the population or the parameter values used to generate the data, β_truth|M_truth . Our simulation code is available as Data S2 for others to explore their own parameter values and/or survey design specifications (number of revisits, sampling intensities, etc.).

Results

Empirical example of a combined analysis

We found that detection probability P-ML and ML estimates for LANO, MYLU, and MYVO were similar (Fig. 2). For LANO, however, the P-ML point estimates of the site-level occupancy parameters differed from the MLEs and also had reduced uncertainty in comparison (Fig. 2). The positive association of LANO occurrence with increasing elevation was only apparent when the sample weights were incorporated into parameter estimation. Estimates for MYVO were slightly different for the intercept and elevation occupancy coefficients, but the uncertainty was quite high for this species. On the other hand, MYLU P-MLE and MLEs were similar; resulting biological inferences would be effectively the same for either approach.

Fig. 2.

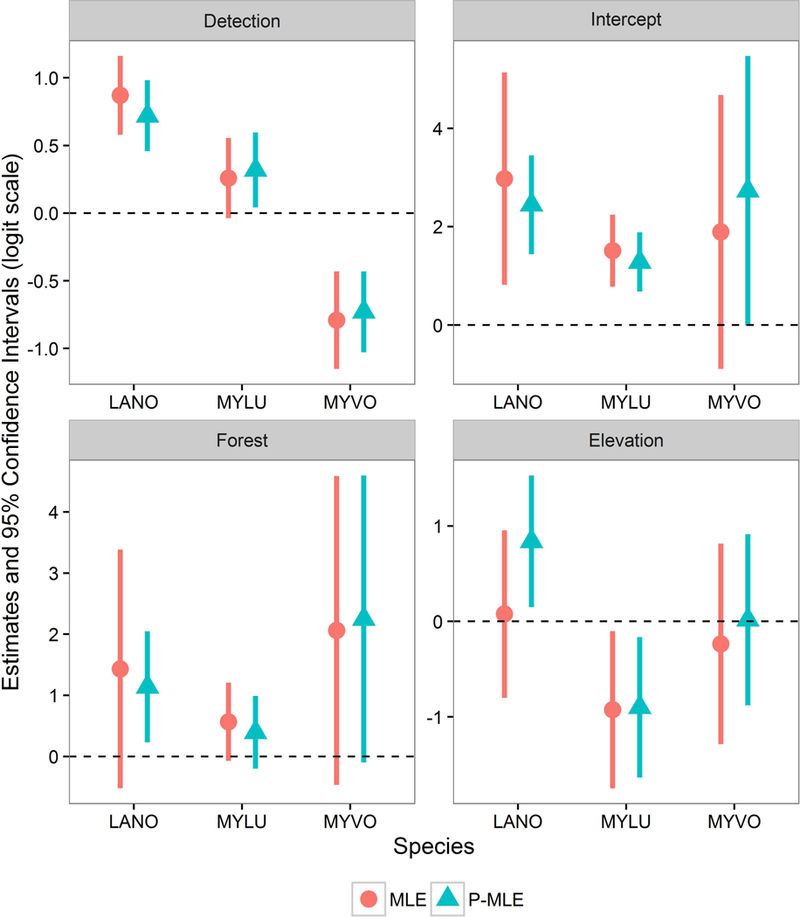
Single-species site-occupancy model fit with constant detection and occupancy covariates of percent forest cover and mean elevation for 3 species of bats, silver-haired bat (LANO; Lasionycteris noctivagans), little brown myotis (MYLU; Myotis lucifugus), and long-legged myotis (MYVO; Myotis volans), observed in 2016 acoustic surveys.

Simulation study

Consistent with the empirical results, detection estimates were similar for P-MLE and MLEs under all models and designs (results not shown). Coverage properties for detection probability (p) estimates were close to the desired 95% for all models and designs using either estimation method. Also, as expected for all fitted models and designs, confidence interval widths increased as sampling intensity decreased and number of revisits was reduced to four (Table 2 results columns denoted by o). However, as sampling intensity decreased to 5% or 10% and 4 revisits, occupancy parameter estimation issues arose with designs dominated by legacy sites or with 50% for the smallest sample size (Table 2 results columns denoted by ∗). Specifically, the standard errors were in f or did not exist after inverting the Hessian matrix. These patterns are likely caused by a combination of variable sample weights and small sample sizes (Table 2). In practice, if the Hessian is not invertible with an empirical analysis, bootstrap or importance sampling could be used to calculate the standard errors (Gill & King 2004).

A hybrid design (legacy and SRS) with 20% sampling intensity and 4 revisits or 10% sampling intensity and 8 revisits produced similar patterns as those based on 20% sampling intensity and 8 revisits (Table 2 denoted by X). Fitting the data generating model resulted in minimal bias for all occupancy parameters (Fig. 3, Elev. + For. first pair of line segments all panels). On the other hand, fitting the non-data generating models resulted in substantially biased MLEs for occupancy coefficient estimates (circles in Fig. 3 not overlapping line segments) that decreased as percentage of legacy sites in the complex survey design decreased (comparing across columns).

Fig. 3.

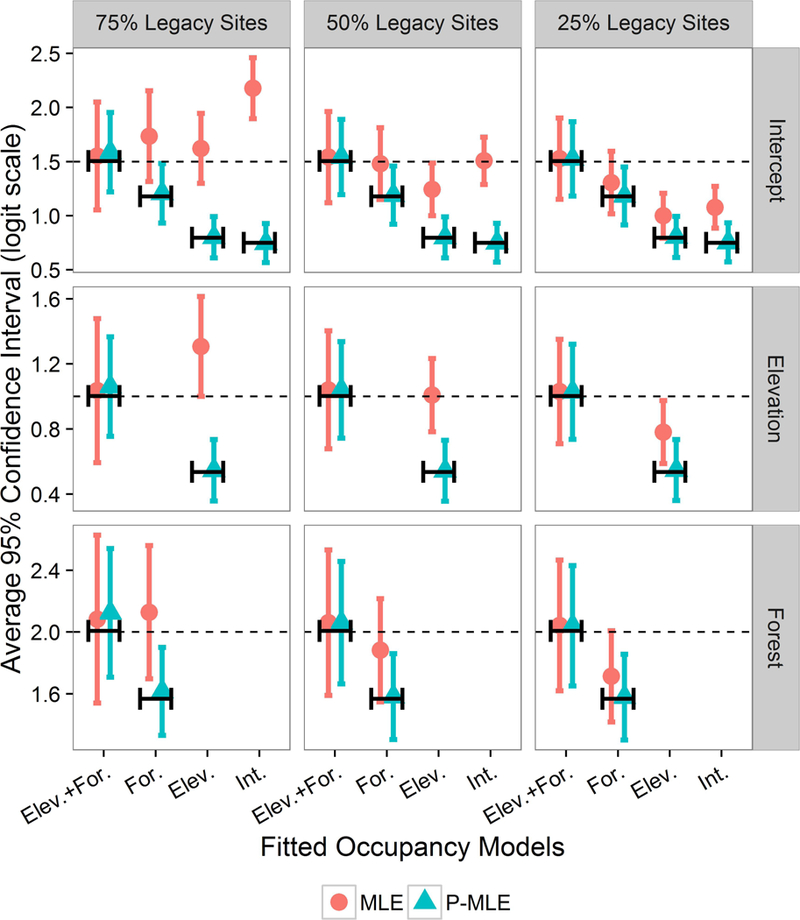
Four different fitted model occupancy parameter estimates under different hybrid design scenarios similar to Oregon example. Fitted models varied site-level covariate structures: data generating model with elevation and percent forest (Elev. + For); Forest cover only (For.); elevation only (Elev.); and constant occupancy (Int.). Each legacy scenario is composed of different percentages (75%, 50%, 25%) of non-probability or purposively selected legacy sites and randomly selected sites for a total sample size of 555 and 8 revisits. Occupancy estimation methods were the usual site-occupancy model with maximum likelihood (MLE) versus weighting the log-likelihood by the adjusted sample weights to account for the design (pseudo-maximum likelihood estimates, P-MLE). The dashed lines display data generating values and line segments show model estimates assuming a census was conducted.

The estimated proportion of area occupied (β₀, Fig. 3 top left panel) with 75% legacy sites was substantially over-estimated due to the fact we selected units with the highest probability of occurrence as legacy sites. For all occupancy parameters, the selection bias was substantially reduced when accounting for the design by incorporating sample weights in estimation (P-MLE, Fig. 3 triangles aligned with census values denoted by line segments). The selection bias decreased as the proportion of legacy sites was reduced (comparison of triangles and circles within a model across columns Fig. 3). However, including sample weights in estimation (P-MLE) does not alleviate model misspecification bias for non-data generating models. Coverage of the true parameter values was not consistent with the desired 95%. The P-ML approach only helped adjust the estimates $({\widehat{\beta }}_{D|M_k})$ towards the average value based on censusing every sample unit (average of ${\widehat{\beta }}_{census|M_k}$).

In general, comparing P-MLE to MLE as a diagnostic for assessing design ignorability given a fitted model lends support to the correct estimation procedure. Further, when the data generating model (Elev. + For.) was fit to data composed of probability and non-probability sites (hybrid designs) the P-MLE were generally the same as MLE (ignorable). However, all other fitted models displayed dramatic differences between MLE and P-MLE for all parameters except the detection probability. These differences were because the non-probability sites were selected because they had the highest probability of species occurrence.

Discussion

Understanding impacts of environmental change on species occurrence patterns across large landscapes that encompass many jurisdictions is increasingly important to contemporary ecology and conservation biology. Aggregating datasets is a way to increase sample size and spatial extent without overburdening any one project or program. Further, requirements for federally funded projects (“Open Access” Office of Science and Technology Policy-White House Memo on Feb. 22, 2013 and “Open Data” Office of Management and Budget-White House Memo on May 9, 2013) and many journals facilitate acquiring datasets from different projects and programs. However, a key statistical concern when analyzing combined datasets should be whether the mechanism used to select sites impacts statistical inferences about species-environment relationships and spatially explicit predictions. If the design is non-ignorable or informative, parameter estimates will be biased because the observed sample is not representative of the target population (Pfeffermann 1993; Winship & Radbill 1994; Kim & Skinner 2013). Our findings and suggestions are predicated on an assumed level of commonality among data contributors as, in our Oregon example (common target population, sample frame, and field protocol); otherwise, reliability of statistical inferences from more disparate survey designs is questionable, more broadly.

We demonstrated that if the probability design is self-weighting, site-level occupancy or detection parameter ML estimators were design unbiased (Appendix S2). With unequal probability sampling, the ML estimator for the intercept parameter was biased when the fitted model excluded the variable related to the design (i.e., elevation Appendix S2). Therefore, with unequal probability designs, if the goal of model-based inference is spatial predictions to unsurveyed locations, the model needs to account for the design by including design-related co-variates in the mean structure or by using the sample weights in the likelihood (P-MLE). However, using an unequal probability design did not affect the estimators for species-environment relationships (MLE and P-MLE were similar, Appendix S2). The designs with probability and non-probability sites resulted in substantially different P-ML and ML estimates for the non-data generating model site occupancy parameters. Therefore, with designs dominated by purposively selected sites, statistical inferences should be based on the P-ML estimators. All our results are conditional on a fitted model because the P-MLE only adjusts for the bias arising from the survey design (design-based bias) and not model misspecification as seen in our simulations and pointed out by Pfeffermann (2011).

In our empirical example, a comparison of P-MLE and MLE results for silver-haired bat (LANO), and possibly long-legged myotis (MYVO), would suggest the hybrid design constructed for 2016 surveys was not ignorable for some species. One viable solution would be to base inferences on P-MLE (Pfeffermann 2011). Alternatively, including additional explanatory variables that might be related to both the hybrid design and LANO or MYVO occurrence could be pursued. Constructing the best approximating model of the ecological process and the sample selection process by incorporating meaningful covariates is another way to account for a non-ignorable design. However, this tactic can be challenging with complex designs and the criticisms pointed out by Pfeffermann (2007) and mentioned in the introduction should be considered. Importantly, for any analysis, we suggest an investigation into whether the design is or becomes ignorable should be considered along with more traditional model assessment approaches (see Appendix S1).

The pseudo-maximum likelihood approach is quite general and can be used to account for non-ignorable survey designs using other specified likelihoods, not solely occupancy models (e.g., Pfeffermann 1993; Winship & Radbill 1994; Pfefferman & Sverchkov 2003; Pfeffermann 2007; Kim & Skinner 2013). For any specified likelihood, other problems for properly estimating species-environment associations can still result from the sampling design specifications. For instance, with the hybrid design scenarios with a high proportion of legacy or non-probability sites, we encountered estimation issues for standard errors with 5% or 10% sampling intensity and 4 revisits. These issues were likely a result of highly variable weights confounded by small sample sizes. Furthermore, small sample sizes within a stratum can also result in computational challenges when including strata indicator variables as fixed effects or partial pooling using random effects to account for the design. The best strategy, therefore, is to avoid sparse representation within certain strata and highly variable weights at the outset. Minimizing the percentage of non-probabilistically selected sample units, if possible, can also mitigate potential issues as well. Code available in Data S2 can be used to explore, and potentially prevent, these issues and to assess whether coverage of the parameter values of interest is achieved for given survey design scenarios with reasonable interval estimates (i.e., sample size calculations for estimating associations). Generally, our results suggest a certain degree of coordination is needed to guarantee the data contributed from outside the probabilistic design (so-called “found” or “legacy” data) is off-set by the probability sites and that representation of environmental gradients of interest are covered sufficiently.

An important consideration for national monitoring programs that propose a master sample as a way to share and coordinate effort within a common probabilistic design is whether sample weights should be included for model-based analyses of aggregated datasets (e.g., To-evs et al. 2011; Loeb et al. 2015; Larsen et al. 2008). If the defined geographic subsets are confounded with a site-level covariate that is related to species occurrence, the final combined design could be non-ignorable depending on the fitted model (see Appendix S2 for more details). These considerations underscore that thoughtful implementation of a master sample and properly tracking data contributors’ decisions to sub-setting are critical, otherwise realized sample weights in a combined design are not recoverable. Aggregating datasets logically shares effort among partners and potentially increases sample size and spatial extent for statistical inferences. However, in order to ensure robust and defensible recommendations for evidence-based conservation decision-making, as desired for NABat, program databases need to track the design information in addition to the data themselves.

Statistical analysts should consider the mechanism of how sample units were selected when interpreting their model-based conclusions. Our results suggest that for known probability sampling designs including variables that account for the design in the mean structure or using the P-MLE should produce design-unbiased inferences. For a design that has a combination of probability and non-probability samples, the P-MLE approach is a reasonable alternative to more complex modeling methods (e.g., Diggle et al. 2010) that jointly model the selection process governing inclusion of spatial units and the ecological processes of interest. We found that the spatial sampling design does not affect model-based estimates, if the data-generating model is specified and the independent variable space is represented in the dataset. The reality for empirical analyses is the data-generating model in unknown, so we develop our “best” approximating model or set of models to describe our system under study. Therefore, in practice, thinking carefully about the covariates becomes an increasingly important step during model building; specifically, which covariates to include, how the covariates are measured relative to the response (both spatial and temporal resolution), and now, whether the sampled locations represent the independent variable (covariate) space of the target population. Importantly, practitioners need to think critically about, and ideally explicitly assess, whether the sampling design is ignorable with any model-based analysis.