Enhancement of Long-Term External–Internal Correlation by Phase-Shift Detection and Correction Based on Concurrent External Bellows and Internal Navigator Signals

Abstract

Purpose

The purpose of this study was to enhance the correlation between external and internal respiratory motions by dynamically determining and correcting the patient-specific phase shift between external and internal respiratory waveforms acquired concurrently during respiratory-correlated 4-dimensional magnetic resonance imaging scans.

Methods and Materials

Internal-navigator and external-bellows waveforms were acquired simultaneously during 6- to 15-minute respiratory-correlated 4-dimensional magnetic resonance imaging scans in 10 healthy participants under an institutional review board–approved protocol. The navigator was placed at the right lung–diaphragm interface, and the bellows were placed ∼5 cm inferior to the sternum. Three segments of each respiratory waveform, at the beginning, middle, and end of a scan, were analyzed. Three phase-domain methods were employed to estimate the phase shift, including analytical signal analysis, phase-space oval fitting, and principal component analysis. A robust strategy for estimating the phase shift was realized by combining these methods in a weighted average and by eliminating outliers (>2 σ) caused by breathing irregularities. Whether phase-shift correction affects the external-internal correlation was evaluated. The cross-correlation between the 2 waveforms in the time domain provided an independent check of the correlation enhancement.

Results

Phase-shift correction significantly enhanced the external-internal correlation in all participants across the entire 6- to 15-minute scans. On average, the correlation increased from 0.45 ± 0.28 to 0.85 ± 0.15 for the combined method. The combined method exhibited a 99.5% success rate and revealed that the phase of the external waveform leads that of the internal waveform in all 10 participants by 57 ^o ± 17^o (1.6 ± 0.5 bins) on average. Seven participants exhibited highly reproducible phase shifts over time, evidenced by standard deviations (σ) < 4^o, whereas 8^o < σ < 12^o in the remaining 3 participants. Regardless, phase-shift correction significantly improved the correlation in all participants.

Conclusions

Correcting the phase shift estimated by the phase-domain methods provides a new approach for enhancing the correlation between external and internal respiratory motions. This strategy holds promise for improving the accuracy of respiratory-gated radiation therapy.

Introduction

Despite substantial progress made in the past 2 to 3 decades, including the advent of fluoroscopic motion-monitoring techniques employing implanted fiducial markers,1, 2, 3, 4, 5 respiratory-correlated 4-dimensional computed tomography (4DCT),6, 7, 8, 9 and, more recently, 4D magnetic resonance imaging (4DMRI),10, 11, 12, 13, 14 managing clinical motion remains one of the biggest challenges in using conventional linear accelerators to treat thoracic and upper abdominal cancers.15, 16, 17 Breathing irregularities are common in lung-cancer patients and degrade both the quality of 4DCT images and the fidelity of tumor delineation.18, 19, 20, 21 Because breathing irregularities also reduce the correlation between the motions of an external-surface surrogate and a mobile tumor, the position of the tumor cannot be reliably inferred from that of the surrogate during treatment delivery without radiographic verification.22, 23, 24 Three general approaches have been advanced to overcome this problem: (1) Updating a correlation-based model with frequent x-ray imaging presents a viable solution,2, 3, 4, 25, 26, 27, 28 but this approach entails the invasive implantation of radio-opaque fiducial markers. (2) Models that employ physical principles to predict respiratory motion should be insensitive to breathing irregularities29, 30, 31, 32 but require a better understanding and more thorough validation of patient-specific breathing patterns. (3) MR-guided radiation therapy33, 34 offers real-time 2D cine imaging but demands substantial investment, staff training, and maintenance resources.

Respiration-induced motions often exhibit nonlinear behaviors, including phase shifts between the motions of an external body surface and internal structures, such as lung or liver tumors. The phase shift can be substantial10, 15, 35 and has been advanced as the most critical irregularity for external-internal models.³⁶ Such a phase shift engenders ellipsoidal trajectories in phase space: This nonlinear relationship illuminates the cause for the low correlation between the two motion waveforms.¹ Because they arise from asynchronized muscle engagement and tissue elasticity, phase shifts are known to be patient specific and location dependent.13, 15, 32, 35, 36, 37, 38 In 4DCT and 4DMRI reconstruction, the phase shift between an external surrogate and an internal-organ motion is mostly ignored15, 16; in fact, a constant phase shift affects only the assignment of a respiratory bin but should not affect the 4D-image quality or the motion assessment. However, a variable phase shift may introduce additional artifacts because of a variable bin assignment. A better understanding and more thorough characterization of the nonlinear features of organ movement are thus essential for building a model that accurately predicts tumor motion.29, 30, 31 Such a model may find application in respiratory gating or in tracking tumors during the delivery of radiation therapy.

In this study we report the feasibility of determining and correcting patient-specific phase shifts to enhance the correlation between external and internal respiratory waveforms. Quantitative estimates of the phase shift were obtained using 3 individual methods, including phase-space oval fitting (POF), principal component analysis (PCA), and analytical signal analysis (ASA). A fourth method excluded outliers (>2 σ) from the individual methods and combined the remaining phase-shift estimates in a weighted average. This approach improved the phase-shift calculation's robustness to breathing irregularities. Maximizing the time-domain cross-correlation between the 2 motion waveforms provided an additional strategy to verify the results obtained by the phase-domain methods. The respiratory waveforms were acquired concurrently by an internal navigator and by external bellows during 4DMRI scans of 10 healthy participants under an institutional review board (IRB)–approved protocol.

Methods and Materials

Simultaneous external and internal waveforms acquired during 4DMRI

Respiratory-correlated 4DMRI scans that employed T2-weighted fast spin-echo sequences were acquired using a 3T MR scanner (Ingenia, Philips Healthcare, Amsterdam, Netherland) in 10 healthy participants under an IRB–approved protocol. During each scan, external-bellows (496 Hz) and internal-navigator (20 Hz) waveforms were acquired concurrently.¹³ The bellows were placed inferior to the sternum, and the navigator (3 × 3 × 6 cm³) was placed on the dome of the right diaphragm. The initial timestamps (in milliseconds) in the scanner and bellows log files were used to synchronize the 2 waveforms with the known frequencies. A 4DMRI scan lasted 6 to 15 minutes, during which 2D coronal slice images were acquired. The navigator signal was used to prospectively sort these slices into 10 respiratory bins using an amplitude-binning method.¹³

Three waveform segments (10-300 s) at the beginning, middle, and end of a scan were divided into 10- or 12.5-second windows that were used for phase-shift assessment. Multiple windows (12.5 seconds) were used in the middle and end segments (Table E1; available online at https://doi.org/10.1016/j.adro.2019.02.001), and each window overlapped with 7.5 seconds of the subsequent window. Employing instead a 7.5-second window confirmed that the phase-shift results were robust to changes in the length of the window. In this case, each window overlapped with only 2.5 seconds of the subsequent window.

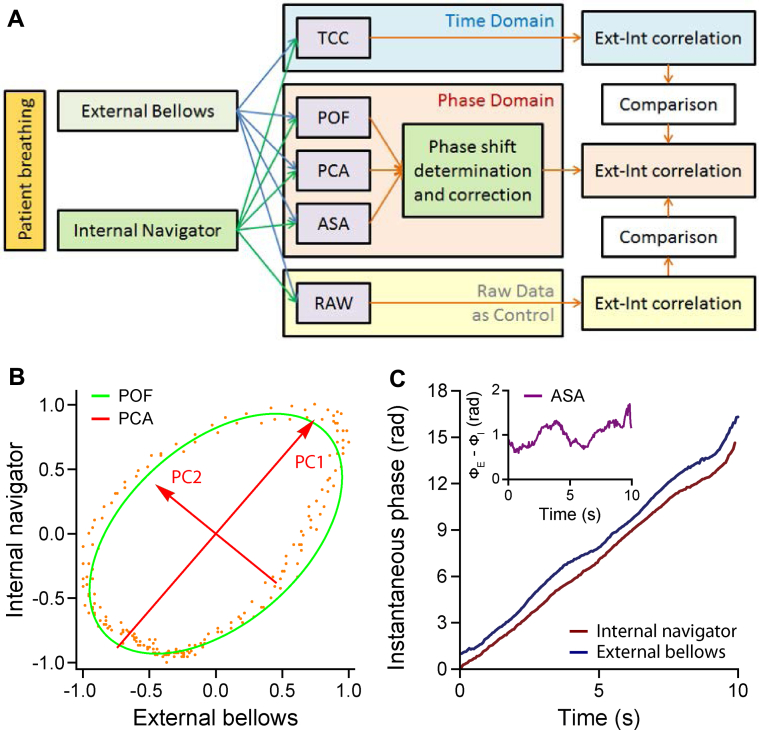
The navigator signal was continuous except at times when slice images were acquired. The bellows waveform was down-sampled to match the navigator's 20-Hz frame rate, and the amplitudes of both waveforms were normalized and centered. The occurrence of ellipsoidal trajectories in phase space (navigator vs bellows) confirmed the existence of a phase shift between the waveforms.¹ Estimates of the phase shift were obtained through POF, PCA, and ASA methods. After correcting the calculated phase shift, the resulting correlation between the 2 waveforms was compared with their original correlation and with the maximum value of their time-domain cross-correlation (TCC) (Fig. 1).

Fig. 1.

(A) Workflow for determining and correcting the phase shift to enhance the correlation between the internal and external waveforms. Three quantitative phase-domain methods were applied, including phase-space oval fitting (POF), principal component analysis (PCA), and analytical signal analysis (ASA). The correlation between the phase-shift–corrected external and internal waveforms was compared with the original correlation and to the waveforms' maximum time-domain cross-correlation (TCC). (B) Representative ellipse and principal components found for participant 2 through the POF and PCA methods, respectively. (C) Representative instantaneous phases of and the phase shift between (inset) the internal and external waveforms calculated for participant 2 using the ASA method. Abbreviations: Ext = external; Int = internal.

Phase-domain methods to assess the phase shift

Three phase-domain methods were implemented in Mathematica (version 10.1; Wolfram) and combined to yield a fourth robust and adaptive strategy for estimating the phase shift.

• (1)POF: The phase shift between the bellows x(t) and navigator y(t) waveforms was calculated from the best-fit oval in phase space (Fig. E1A; available online at https://doi.org/10.1016/j.adro.2019.02.001). In this space, an ellipse centered at (0,0) is described by

$$\frac{{\left(\mathit{x}\cos \mathit{\theta }+\mathit{y}\sin \mathit{\theta }\right)}^2}{{\mathit{a}}^2}+\frac{{\left(\mathit{y}\cos \mathit{\theta }-\mathit{x}\sin \mathit{\theta }\right)}^2}{{\mathit{b}}^2}=1\text{,}$$ (Eq. 1)

where a and b are the major and minor half-axis lengths and θ is the angle by which the major axis is tilted clockwise from the positive x-axis. For simplicity, we modeled the waveforms as 2 sinusoidal functions x(t) = r₁ cos (ω₁ t) and y(t) = r₂ cos (ω₂ t+ϕ) with phase shift ϕ and assuming ω₁ = ω₂ = ω. The phase shift is given by

$$\varphi ={\tan }^{-1}\left[\frac{\mathit{ab}\sec \mathit{\theta }}{\left({\mathit{a}}^2-{\mathit{b}}^2\right)\sin \mathit{\theta }}\right]$$ (Eq. 2)

The residual error (RE) in a phase-space ellipse's fit of the data points {x_j,y_j} is given by

$$\mathit{RE}=\frac{1}{\mathit{n}}\sum _{\mathit{j}=1}^{\mathit{n}}\underset{{\mathit{\alpha }}_{\mathit{j}}}{\min }\sqrt{{\left({\mathit{x}}_{\mathit{j}}-{\mathit{r}}_1\cos \left[{\mathit{\alpha }}_{\mathit{j}}\right]\right)}^2+{\left({\mathit{y}}_{\mathit{j}}-{\mathit{r}}_2\cos \left[{\mathit{\alpha }}_{\mathit{j}}+\varphi \right]\right)}^2}$$ (Eq. 3)

An explanation of how the sign of ϕ is determined and detailed deviations of Equations (Eq. 2), (Eq. 3) are provided in Appendix E1 (available online at https://doi.org/10.1016/j.adro.2019.02.001).

• (2)PCA: A 2 × n matrix A = (bellows: x (t), navigator: y (t)) was constructed from the 2 concurrent waveforms and the covariance matrix for this data set was formed by the multiplication AA^T/(n−1). The principal components, ${\overrightarrow{\mathit{p}}}_1$ and${\overrightarrow{\mathit{p}}}_2$, were given by the eigenvectors of the covariance matrix. The square roots of the eigenvalues, $\sqrt{{\mathit{\lambda }}_1}$ and$\sqrt{{\mathit{\lambda }}_2}$, represented the standard deviation in the data set in the directions of the principal component vectors. An ellipse was then constructed with major and minor axes pointing in the directions of ${\overrightarrow{\mathit{p}}}_1$ and ${\overrightarrow{\mathit{p}}}_2$ and with half lengths $\mathit{a}=\sqrt{{\mathit{\lambda }}_1}$ and $\mathit{b}=\sqrt{{\mathit{\lambda }}_2}$, respectively (Fig. E1A; available online at https://doi.org/10.1016/j.adro.2019.02.001). The tilt angle of the ellipse was given by $\mathit{\theta }={\tan }^{-1}\left[{\overrightarrow{\mathit{p}}}_{1,\mathit{y}}/{\overrightarrow{\mathit{p}}}_{1,\mathit{x}}\right]$ and the phase shift ϕ by Equation 2. See Appendix E2 (available online at https://doi.org/10.1016/j.adro.2019.02.001) for additional details.
• (3)ASA: An analytical representation of a real-valued function, called the function's analytical signal, can be constructed as follows:

$${\mathit{f}}_{\mathit{A}}\left(\mathit{t}\right)=\mathit{f}\left(\mathit{t}\right)+{\mathit{if}}_{\mathit{H}}\left(\mathit{t}\right)$$

where f(t) is the original function, f_H(t) is the Hilbert transform of f(t), and f_A(t) is the analytical signal of f(t). The discrete Fourier $\left(ℱ\right)$ and inverse Fourier $\left({ℱ}^{-\text{1}}\right)$ transforms were employed to calculate the Hilbert transforms for the discrete signals:

$${\mathit{f}}_{\mathit{H}}\left(\mathit{t}\right)={ℱ}^{-1}\left\{-\mathit{i}\mathrm{sign}\left(\mathit{\omega }\right)ℱ\left\{\mathit{f}\left(\mathit{t}\right)\right\}\left(\mathit{\omega }\right)\right\}\left(\mathit{t}\right)\text{;}\mathrm{sign}\left(\mathit{\omega }\right)=\{\begin{array}{c}1,\mathrm{if}\omega >1\\ 0,\mathrm{if}\omega =0\\ -1,\mathrm{if}\omega <1\end{array}$$

The instantaneous phase of a signal at time t_k, ϕ (t_k) is found from its analytical signal:

$$\mathit{\varphi }\left({\mathit{t}}_{\mathit{k}}\right)={\tan }^{-1}\left[\frac{\mathrm{Im}{\mathit{f}}_{\mathit{A}}\left({\mathit{t}}_{\mathit{k}}\right)}{\mathrm{Re}{\mathit{f}}_{\mathit{A}}\left({\mathit{t}}_{\mathit{k}}\right)}\right]={\tan }^{-1}\left[\frac{{\mathit{f}}_{\mathit{H}}\left({\mathit{t}}_{\mathit{k}}\right)}{\mathit{f}\left({\mathit{t}}_{\mathit{k}}\right)}\right]$$ (Eq. 4)

Then $\Delta \mathit{\varphi }\left({\mathit{t}}_{\mathit{k}}\right)={\mathit{\varphi }}_1\left({\mathit{t}}_{\mathit{k}}\right)-{\mathit{\varphi }}_2\left({\mathit{t}}_{\mathit{k}}\right)$ is the instantaneous phase shift between these 2 signals and averaging over a set of data points yields the mean phase shift $\varphi =\langle \Delta \mathit{\varphi }{\left({\mathit{t}}_{\mathit{k}}\right)\rangle }_{{\mathit{t}}_{\mathit{k}}}$ for the interval containing the time points t_k (Fig. E1B; available online at https://doi.org/10.1016/j.adro.2019.02.001).

A combined method to calculate a mean phase shift (MPS)

Breathing irregularities may cause the individual methods to yield unreliable results. More reliable estimates therefore can be obtained from a combined method that excludes individual-method outliers. A moving average was initialized by weighting the phase-shift estimates at time zero by the reciprocal of their RE. A larger RE value indicates that the phase-shift estimate in that time window is less reliable. For a given time window, the calculation therefore gives greater weight to the estimation methods that yield smaller RE values and thus more reliable phase-shift estimates. Because breathing irregularities affect the phase-shift estimation methods in different ways, this weighting strategy minimizes the idiosyncratic responses of the individual methods, yielding a more robust estimation of the phase shift.

At each successive time point, the phase shift was estimated by halving the weighted average of the phase shifts calculated by the individual methods at the current time point and adding the result to half of the previous moving average value. A moving standard deviation σ was calculated as the average standard deviation of the individual phase shifts found at all the previous time points. Numerical simulations of noisy sinusoids revealed a strong correlation between the RE and the true error in the phase-shift estimate (Fig. E1; available online at https://doi.org/10.1016/j.adro.2019.02.001). This analysis also informed the choice that RE = 0.2 would serve as the maximum tolerable threshold (Appendix E2; available online at https://doi.org/10.1016/j.adro.2019.02.001). An outlier was defined to be a phase shift estimated by an individual method whose value was more than 2σ away from the running average and whose RE for the associated phase-space ellipse exceeded 0.2.

TCC method

The cross-correlation in the time domain, TCC(τ_j), between the 2 signals was calculated as follows:

$$\text{T}\text{C}\text{C}\left({\mathit{\tau }}_{\mathit{j}}\right)=\frac{{\sum }_{\mathit{k}=1}^{\mathit{N}}{\mathit{s}}_{\mathit{I}}\left({\mathit{t}}_{\mathit{k}}+{\mathit{\tau }}_{\mathit{j}}\right){\mathit{s}}_{\mathit{E}}\left({\mathit{t}}_{\mathit{k}}\right)-{\sum }_{\mathit{k}=1}^{\mathit{N}}{\mathit{s}}_{\mathit{I}}\left({\mathit{t}}_{\mathit{k}}+{\mathit{\tau }}_{\mathit{j}}\right){\sum }_{\mathit{i}=1}^{\mathit{N}}{\mathit{s}}_{\mathit{E}}\left({\mathit{t}}_{\mathit{i}}\right)}{\sqrt{{{\sum }_{\mathit{k}=1}^{\mathit{N}}\left[{\mathit{s}}_{\mathit{I}}\left({\mathit{t}}_{\mathit{k}}+{\mathit{\tau }}_{\mathit{j}}\right)-{\sum }_{\mathit{i}=1}^{\mathit{N}}{\mathit{s}}_{\mathit{I}}\left({\mathit{t}}_{\mathit{i}}+{\mathit{\tau }}_{\mathit{j}}\right)\right]}^2}\sqrt{{{\sum }_{\mathit{k}=1}^{\mathit{N}}\left[{\mathit{s}}_{\mathit{E}}\left({\mathit{t}}_{\mathit{k}}\right)-{\sum }_{\mathit{i}=1}^{\mathit{N}}{\mathit{s}}_{\mathit{E}}\left({\mathit{t}}_{\mathit{i}}\right)\right]}^2}}$$ (Eq.5)

where the number of points N was a subset of that contained within the time window, s_I is the navigator signal, and s_E is the bellows signal. TCC(0) gives the original correlation between the external and internal waveforms. Multiplying the frequency of the bellows or navigator waveforms by the value of τ_j that maximizes TCC(τ_j) provides another estimate of the phase shift between the 2 signals. The frequency of the waveforms was found in the following 4 ways: the frequency at which the power spectrum of the (1) bellows or (2) navigator signals achieved their maximum value, and the average slope of the (3) bellows' or (4) navigator's instantaneous phase. The correlation coefficient between each pair of frequency estimates exceeded 0.9, indicating that any of the 4 estimates worked equally well at most time points. When a discrepancy existed between these estimates, the frequency that maximized the phase-shift–corrected correlation, described later, was chosen.

Diaphragm-motion phase shifts between navigator-triggered and bellows-rebinned 4DMRI

Following previously reported methods, 2 binning strategies were employed to produce 2 different 4DMRI images.¹³ Sorting the 2D slices into 10 respiratory bins based on the amplitude of the internal navigator generated the navigator-triggered 4DMRI image. The bellows-rebinned 4DMRI image was constructed by instead using the amplitude of the concurrently acquired external-bellows signal to sort the 2D slices into the 10 bins. Two diaphragm-motion trajectories were then obtained by manually tracking the position of the right diaphragm dome's apex in both 4DMRI images through the breathing cycle. The 2 trajectories are functions of phase-bin number. A cross-correlation analysis was performed to identify the phase shift that arose between the 2 different 4DMRI images for each participant.

1D phase-shift correction for improved external-internal correlation

To correct the phase shift estimated by the 1D methods within each time window, the navigator signal was shifted in time by an amount equal to the calculated phase shift divided by the waveform's frequency. The frequency of the waveform was estimated in 4 ways, as described in a previous section. At each time point, the frequency estimate was chosen to maximize the correlation between the waveforms after phase-shift correction. By comparing the correlation coefficient for the original waveforms with that of the phase-shift–corrected waveforms, we assessed whether correcting the phase shift enhanced the correlation between the internal and external signals.

Results

Patient-specific phase shifts

The calculated phase shifts spanned a broad range of 0.5 to 1.7 radians using the mean phase shift (MPS) method (Table 1). By excluding outliers and averaging the phase shifts obtained by the ASA, POF, and PCA methods, the MPS method yielded a smoother and more robust estimate (Fig. 2A, Fig. E2 [available online at https://doi.org/10.1016/j.adro.2019.02.001]). Because of their different assumptions and varied sensitivity to noise and breathing irregularities, each method yielded slightly different phase-shift estimates. However, these phase shifts were strongly correlated: Pearson's correlation coefficient r exceeded 0.8 for every pair of methods, except r = 0.77 for the maximum TCC and ASA methods. The mean phase shift, averaged across participants, was 0.99 ± 0.30 radians for the 12.5-second window length and 0.98 ± 0.31 radians for the 7.5-second window length. The phase shifts obtained by the 2 window lengths closely agreed for the vast majority of the time windows: the mean absolute difference—averaged across participants—was 0.07 ± 0.04 radians.

Table 1.

Phase shifts (mean ± standard deviation in radians) estimated in the phase, time, and image domains

Participant	ASA	POF	PCA	MPS	Max TCC	Image
1	0.65 ± 0.03	0.83 ± 0.04	0.65 ± 0.02	0.70 ± 0.02	0.68 ± 0.06	0.6
2	1.03 ± 0.10	1.03 ± 0.08	0.99 ± 0.05	1.02 ± 0.04	0.98 ± 0.07	1.0
3	0.52 ± 0.06	0.84 ± 0.12	0.59 ± 0.06	0.62 ± 0.05	0.60 ± 0.05	0.5
4	1.31 ± 0.22	1.47 ± 0.17	1.34 ± 0.19	1.37 ± 0.17	1.27 ± 0.19	-∗
5	0.49 ± 0.09	0.73 ± 0.14	0.59 ± 0.10	0.62 ± 0.05	0.48 ± 0.07	0.3
6	0.91 ± 0.20	1.05 ± 0.10	0.87 ± 0.11	0.97 ± 0.06	0.67 ± 0.17	0.8
7	1.05 ± 0.17	1.13 ± 0.06	1.08 ± 0.11	1.08 ± 0.07	0.97 ± 0.18	0.4
8	1.50 ± 0.32	1.54 ± 0.06	1.63 ± 0.10	1.56 ± 0.06	1.29 ± 0.42	1.6
9	0.84 ± 0.25	1.12 ± 0.15	0.97 ± 0.19	0.96 ± 0.20	0.86 ± 0.21	0.7
10	1.05 ± 0.15	1.11 ± 0.26	0.89 ± 0.19	1.01 ± 0.14	0.72 ± 0.13	1.0
Mean†	0.93 ± 0.33	1.08 ± 0.26	0.96 ± 0.33	0.99 ± 0.30	0.85 ± 0.27	0.77

Abbreviations: ASA = analytical signal analysis; PCA = principal component analysis; POF = phase-space oval fitting; MPS = mean phase shift; TCC = time-domain cross-correlation.

Results are shown for the 12.5-second window length.

^∗Severe breathing irregularities make the peak of the bellows waveform difficult to discern.

^†Averaged over all participants' mean phase shifts.

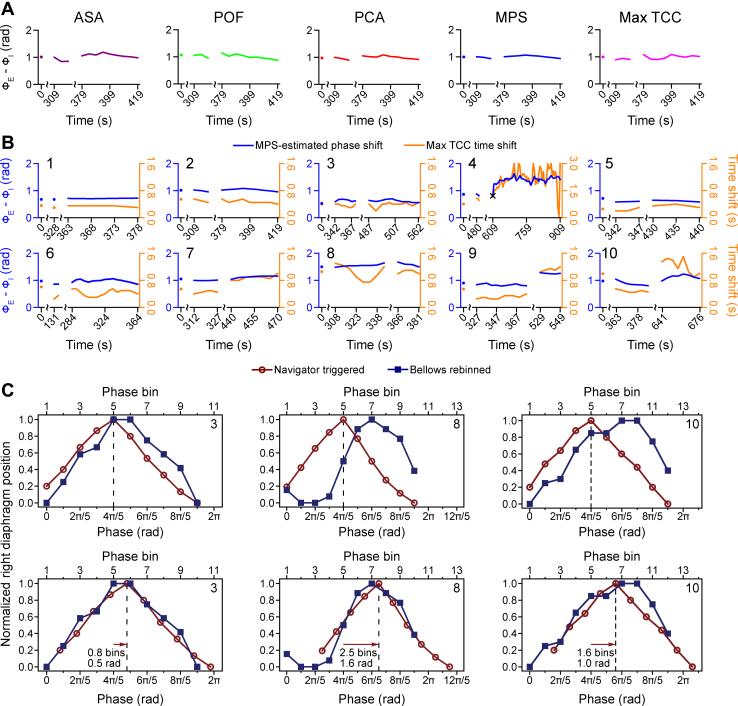
Fig. 2.

Participant-specific phase shifts determined by six methods. (A) Phase shift over time for participant 2 calculated every 5 seconds using the analytical signal analysis (ASA, purple), phase space oval-fitting (POF, red), principal component analysis (PCA, green), combined mean phase shift (MPS, blue), or maximum time-domain cross-correlation (Max TCC, magenta) method. Phase-shift curves for all ten participants are portrayed in Figure E2 (available online at https://doi.org/10.1016/j.adro.2019.02.001). (B) Phase shifts (blue) over time for 10 participants calculated using the combined method. The time shifts (orange) that maximize the time-domain cross-correlation are also shown. The × in the panel for participant 4 indicates the single time point across all participants at which the combined method failed. (C) Representative phase shifts estimated from measured diaphragm motions. Trajectories were obtained from navigator-triggered (dark-red circles) and bellows-rebinned (dark-blue squares) 4-dimensional magnetic resonance images before (upper panels) and after (lower panels) phase alignment for participants 3 (left), 8 (middle), and 10 (right). The dark-red arrows indicate the estimated phase shift. Except where indicated by scale breaks, consecutive data points occur at 5-second intervals and are joined via linear interpolation in panels A and B.

The external-bellows signal was found to lead the motion acquired by the internal navigator in the 10 participants by all 5 waveform methods (Table 1, Fig. 2). The analysis also revealed that an individual's phase shift could be relatively stable over several minutes (Fig. 2B, blue curves). Changes in the phase shift can occur, however, when a participant alters his or her breathing pattern. For example, asking participants 4 and 9 to take deep breaths near the end of the scans precipitated a nearly 0.5-radian change in their phase shifts. The time shift that maximizes the time-domain cross-correlation was found to be more variable than the estimated phase shift (Fig. 2B, orange curves). This variability arises from changes in the frequency of a participant's breathing, but apparently the 2 effects balance to yield a stable phase shift (Fig. E2; available online at https://doi.org/10.1016/j.adro.2019.02.001).

Phase shift determined from tracking points in 4DMRI images

The phase shift measured between the diaphragm trajectories based on navigator-triggered and bellows-rebinned respiratory-correlated 4DMRI images also revealed that the phase of the bellows waveform leads that of the navigator signal (Fig. 2C, Table 1). Because it collects into bins images at various times throughout the scan, this approach can estimate only an average phase shift. That close agreement between the 4D-imaging and 1D-waveform methods was found for 6 participants indicates that the phase shift was stable in time for these individuals. The discrepancy identified for the other 4 participants may stem from breathing irregularities and the fact that the 4D image and 1D signal were not acquired exactly at the same time—that is, the navigator waveforms were not recorded during image acquisition. The 4D-imaging method can accurately estimate the average phase shift only if the shapes of the navigator and bellows waveforms are similar and are stable in time. Pronounced irregularities in the bellows waveform acquired for participant 4 led to a relatively flat diaphragm-motion trajectory in the bellows-rebinned 4DMRI image. Because of these large uncertainties, the cross-correlation analysis yielded an unreliable phase-shift estimate in this participant (Table 1).

Enhanced motion correlation with phase-shift correction

An improved correlation between the internal-navigator and external-bellows signals was found for every participant after phase-shift correction. On average, the correlation was enhanced from 0.45 ± 0.28 to 0.85 ± 0.15 for the 12.5-second window length (to 0.88 ± 0.18 for the 7.5-second window length), and to more than 0.9 for 5 participants (Table 2, Fig. 3B). The improvement appeared to be systematic because an enhanced correlation was found in nearly every time window (Fig. E3; available online at https://doi.org/10.1016/j.adro.2019.02.001). Interestingly, an improved correlation was achieved even for the only time window in which all 3 phase-domain methods failed if the phase shift for the previous time window was used.

Table 2.

Correlation (mean ± standard deviation) before and after phase-shift correction

Participant	Original	ASA	POF	PCA	MPS	Max TCC
1	0.76 ± 0.03	0.95 ± 0.01	0.93 ± 0.02	0.95 ± 0.01	0.95 ± 0.01	0.95 ± 0.01
2	0.52 ± 0.07	0.93 ± 0.03	0.92 ± 0.03	0.93 ± 0.03	0.93 ± 0.03	0.91 ± 0.04
3	0.84 ± 0.03	0.97 ± 0.02	0.92 ± 0.04	0.97 ± 0.02	0.96 ± 0.02	0.97 ± 0.02
4	0.19 ± 0.16	0.75 ± 0.20	0.80 ± 0.17	0.80 ± 0.19	0.78 ± 0.21	0.93 ± 0.04
5	0.86 ± 0.03	0.93 ± 0.03	0.88 ± 0.05	0.92 ± 0.03	0.92 ± 0.03	0.95 ± 0.01
6	0.58 ± 0.10	0.86 ± 0.11	0.86 ± 0.09	0.88 ± 0.08	0.87 ± 0.08	0.85 ± 0.08
7	0.52 ± 0.09	0.91 ± 0.05	0.89 ± 0.07	0.91 ± 0.06	0.91 ± 0.06	0.92 ± 0.02
8	0.09 ± 0.08	0.69 ± 0.10	0.69 ± 0.10	0.69 ± 0.10	0.69 ± 0.10	0.74 ± 0.07
9	0.56 ± 0.14	0.86 ± 0.06	0.83 ± 0.07	0.85 ± 0.07	0.84 ± 0.06	0.85 ± 0.08
10	0.52 ± 0.18	0.75 ± 0.16	0.81 ± 0.11	0.85 ± 0.07	0.83 ± 0.09	0.85 ± 0.08
Mean∗	0.45 ± 0.28	0.83 ± 0.16	0.84 ± 0.14	0.85 ± 0.14	0.85 ± 0.15	0.90 ± 0.08

Abbreviations: ASA = analytical signal analysis; PCA = principal component analysis; POF = phase-space oval fitting; MPS = mean phase shift; TCC = time-domain cross-correlation.

Results are shown for the 12.5-second window length.

^∗Averaged over all 192 time windows.

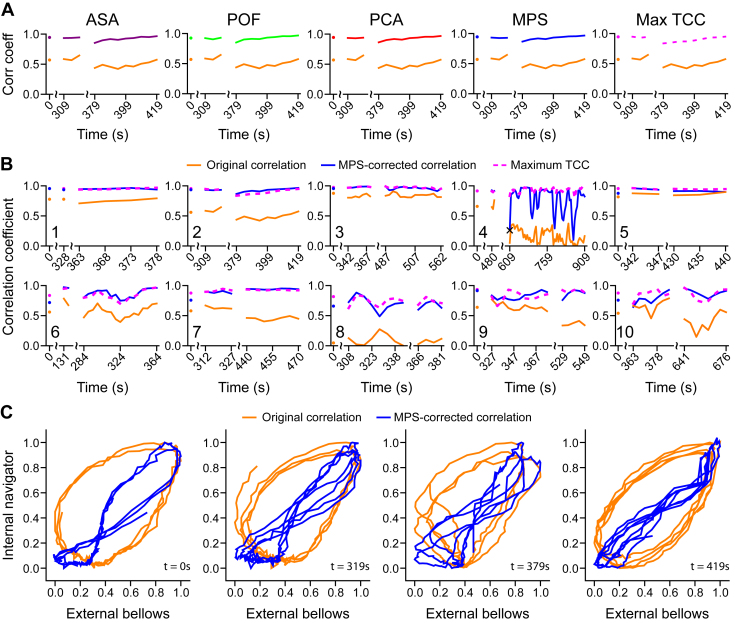
Fig. 3.

Correlation enhancement via phase-shift correction calculated every 5 seconds. (A) Correlation over time between the internal-navigator and external-bellows signals for participant 2 before (orange) and after phase-shift correction using the analytical signal analysis (ASA, purple), phase space oval-fitting (POF, red), principal component analysis (PCA, green), mean phase shift (MPS, blue), and maximum time-domain cross-correlation (Max TCC, dashed, magenta) methods. (B) Correlation enhancement over time for all participants using the MPS method (blue). The cross-correlation is also shown for comparison (dashed, magenta). (C) Phase-shift correction causes the phase-space oval (orange) to collapse (blue) for participant 2, providing a visual indication of the improved correlation. The enhanced correlation is stable (B2) despite breathing irregularities (C, Video E1; available online at https://doi.org/10.1016/j.adro.2019.02.001). Except where indicated by scale breaks, consecutive data points occur at 5-second intervals and are joined via linear interpolation.

The time-domain cross-correlation analysis provided comparable values to those obtained by correcting the phase shift (Table 2, Fig. 3B). The maximum TCC and MPS results are in close agreement (the final correlation coefficients differ by less than 0.1 for 87% of the time windows), except for participants 4 and 8, the individuals with the largest phase shifts (1.27 and 1.29 radians) and thus the lowest uncorrected correlations (r = 0.19 and 0.09). Although correcting their phase shifts effected the greatest relative correlation enhancement, the maximum TCC results suggest that further improvement may be possible for these participants. In 50% of the time windows, correcting the phase shift yields an enhanced correlation that slightly exceeds the maximum cross-correlation estimated by the max TCC method (Figs. 3B and E3 [available online at https://doi.org/10.1016/j.adro.2019.02.001]). This occurs because the max TCC method uses an effectively shorter time window (Eq. 5) than that employed by the phase-domain methods.

Correcting the phase shift causes the ellipsoidal phase-space trajectory to collapse into a more linear shape, which graphically illustrates the improved correlation (Fig. 3C, Video E1 [available online at https://doi.org/10.1016/j.adro.2019.02.001]). The phase-space representation also grants a view into breathing irregularities: Although the positions or orientations of the phase-space trajectories may vary considerably, the phase shift remains stable. The Mann-Whitney U test revealed that the difference between the original and phase-shift corrected correlations and that between the original correlation and the maximum TCC was statistically significant in all participants (Fig. 4A). The phase-shift estimation strategy is also robust: The combined method failed in only a single time window and the success rate exceeded 95% for each of the individual methods (Table E1 [available online at https://doi.org/10.1016/j.adro.2019.02.001], Fig. 4B).

Fig. 4.

(A) Correlation coefficient averaged across all time points before (orange) and after (blue) phase-shift correction, together with the average maximum time-domain cross-correlation (Max TCC) value (striped, magenta). Phase-shift correction yielded a statistically significant enhancement of the correlation in all participants (*P < .05, ***P < .005, Mann-Whitney U test). The error bars represent 1 standard deviation. (B) Robustness (99.5% success rate) of the combined phase-domain method compared with the individual methods. Abbreviations: ASA = analytical signal analysis; PCA = principal component analysis; POF = phase space oval fitting; MPS = mean phase shift.

Discussion

Based on clinical observations,1, 13, 29 it was reasonable to hypothesize that some patient-specific respiratory features, including the phase shift, may remain invariant over several minutes during a single imaging or treatment session. Correcting the persistent patient-specific phase shift was therefore expected to improve the correlation between the internal- and external-respiratory motions over that period.

Patient-specific phase shift in phase, time, and image domains

In total, 6 different methods (POF, PCA, ASA, MPS, maximum TCC, and image-based trajectory), drawn from the phase, time, and image domains, were employed to determine the patient-specific phase shift between concurrent external-bellows and internal-navigator waveforms. Unlike the maximum TCC method that operates in the time domain, assessing phase shifts in the phase domain does not require estimates of the breathing frequency. In the image domain, an averaged phase shift can be extracted retrospectively. The close agreement found for the correlation enhancement among these methods suggests an accurate assessment of the phase shift and accords with the proposition that the phase shift constitutes the primary cause of the originally weak correlation.

Phase shifts, which should depend on the nature of the participant's breathing pattern³⁰ and on the placement of the external bellows,38, 39 were identified in all 10 participants. The thoracoabdominal movements are initiated by the diaphragm or abdominal and intercostal muscles. These structures therefore bear on the breathing pattern, which refers to the ratio of thoracic to abdominal involvement during respiration. Even when placed inferior to the xiphoid of the sternum, the bellows may detect the motion of the inferior ribs, resulting in a complex motion pattern. This might explain the large phase shifts found for several participants, similar to previous reports.13, 15, 35, 38 Lastly, the MR navigator echo allows us to monitor respiratory motion for 6 to 15 minutes, a time frame that is similar to radiation-therapy treatments and much longer than the 30- to 60-second windows usually employed in fluoroscopic imaging.2, 40

Because the navigator signal is temporarily unavailable during image acquisition, the navigator signal, unlike the bellows waveform, is fragmented and incomplete: The navigator is active and able to collect data only when the MR scanner is waiting to populate an unfilled respiratory-amplitude bin with an image slice. Consequently, the number of time segments varies across participants. For participants who exhibit regular breathing patterns, the image-acquisition algorithm proceeds with few interruptions, and fewer time windows are obtained. Conversely, a greater number of time windows are obtained for participants—such as participant 4—who exhibit irregular breathing patterns as more time elapses before images slices have been acquired for each of the respiratory-amplitude bins. Nevertheless, time windows were obtained for every participant at the beginning, middle, and end of the MRI scan. This set of samples adequately determined that the phase shift remains stable over several minutes.

The patient-specific phase shift is stable and correctable

Two periodic waveforms with differing phases will consistently move in opposite directions at certain times during their cyclical motions. Such a phase shift was recognized as the most critical irregularity for external-internal models.³⁶ We found that the phase shift is stable in time and that the phase shift—not random irregularities—is the primary cause for the low correlation between the internal and external waveforms (0.45 ± 0.28). After phase-shift correction, the correlation was significantly improved in all participants (0.85 ± 0.16). This finding indicates the importance and feasibility of detecting and correcting a dynamic phase shift to establish a robust external-internal motion model for respiratory-gated radiation therapy.

Obtaining similar correlation enhancements through disparate methods provided solid cross verification that the phase shifts were accurately estimated. The time shift estimated by the max TCC method was more variable than the phase shift estimated by the MPS method, suggesting that the phase shift is a more fundamental property of an individual's breathing pattern. Although the performances of these methods are comparable, focusing on the phase shift, rather than on the more variable time shift, may allow algorithms that correct the shift between respiratory waveforms to update less frequently while steadily achieving an enhanced correlation.

Because the PCA method performed best out of the phase-domain methods (Fig. 4B) and produced results that were nearly identical to those produced by the MPS method (Table 2), it is possible to simplify the phase-shift estimation strategy to employ this single approach. However, the POF and ASA methods yielded greater correlation improvements than the PCA method in several time windows. By incorporating all 3 estimates, the MPS method is thus equipped to attain greater robustness than any individual method.

The temporal resolution of the phase-shift calculation

The temporal resolution of the phase-shift calculation is approximately equal to the length of the time window. The window length mediates a tradeoff between the degree of correlation enhancement and the variability of results across windows: The increasing amount of irregularity contained within longer time windows diminishes the degree by which the correlation between waveforms can be enhanced, but employing a longer window yields smoother phase-shift results. Clinically, the window lengths should encompass at least 1 breathing cycle. The similarity of the results obtained from the 12.5-second and 7.5-second window lengths suggests that either is a reasonable choice.

The methods track slow changes in the phase shift well but lag behind abrupt changes by the length of 1 time window. The close agreement between the phase shifts estimated by the phase-domain and time-domain methods together with the small number of sharp declines identified in the corrected correlation suggest, however, that rapid changes in the phase shift occur only rarely and that the temporal resolution of the combined method is adequate to track changes in the phase shift. To allow for adaptive motion correction, the phase-shift estimation should be checked periodically during a treatment; if the phase shift is found to change, then the new phase shift will replace the initial phase-shift estimate. The fact that the phase shift remains steady over 6 to 15 minutes for most participants suggests a simple solution to improve patient-motion management for respiratory-gated radiation therapy.

In the single time window that all 3 phase-space methods failed, the phase-space trajectory resembled 2 disparately oriented ovals that, together, could not be accurately represented by a single ellipse. After subdividing this time window into 2 parts that each contained only 1 of these ovals, the combined method succeeded in estimating phase shifts of approximately 1.45 radians, values that are similar to the phase shifts found for subsequent time windows. The sudden reorientation of the phase-space trajectory during this time window may reflect an abrupt change in the participant's breathing pattern or in the baseline position of the diaphragm or epigastrium. Although the phase shift seems unaffected, these changes can result in failure of the phase-shift estimation strategy. However, using the phase shift from the preceding time window substantially improves the correlation.

Estimating the breathing frequency

Accurate estimates of a participant's breathing frequency are needed to correct the phase shift. Because each 7.5-second or 12.5-second time window contains only 1 or 2 breathing cycles, reliable estimates were obtained by employing multiple frequency-estimation strategies; the best frequency estimates were obtained from a signal's Fourier transform in 70% of time windows and from the average slope of the analytical signal's argument in the remaining windows. These strategies closely agreed for the vast majority of time windows, indicating that any option provides a reasonable estimate of the breathing frequency most of the time. There were, however, 8 time windows in which the agreement was poor (Fig. E2; available online at https://doi.org/10.1016/j.adro.2019.02.001). The phase-domain methods are critical in these instances: The frequency estimate that maximizes the phase-shift–corrected correlation is used. The phase-domain methods thus allow the phase-shift correction algorithm to select the best frequency-estimation strategy for a given time window. Because the correlation coefficient is used to calculate the time shift, the maximum TCC method—when used alone—is unable to select the best frequency-estimation strategy and consequently is unable to identify the most accurate phase shift when discrepancies arise between the frequency-estimation strategies.

Clinical implication of a phase-corrected external surrogate

In this study of healthy participants, the internal-motion target was the diaphragm, which can serve only as an internal-motion surrogate for a lung or liver tumor. In a future patient study, we can explore the feasibility of placing the internal navigator on a sizable tumor to obtain a direct measurement of the phase shift between the motions of the tumor and bellows. Alternatively, we can employ the super-resolution, time-resolved 4DMRI in a patient study because it can measure a tumor's motion at a 2-Hz frame rate.¹⁴ To meet various clinical needs, the dynamic MR imaging data can be used to build either a simple phase-shift–corrected respiratory model or a sophisticated physics-based perturbation model that incorporates the movement of the entire torso's surface through optical imaging.41, 42

Using an external respiratory surrogate, clinical 4DCT and some 4DMRI are acquired, binned, and reconstructed.15, 16 If there is a near-constant phase shift between the external-surrogate and internal-organ motions, the apparent effect is a “bin shift” in the 4D reconstruction. However, if the phase shift varies substantially from time to time, then the bin assignment of an image may vary, resulting in additional binning-motion artifacts. On the other hand, if an internal surrogate—such as an MR navigator—can be used, then the correlation uncertainty is eliminated and the 4D image quality should consequently be better, as was reported previously.¹³

In addition, the correlation-enhancement analysis indicates that the phase shift was adequately corrected in 9 out of 10 participants. The data from 8 participants suggest that the phase-shift–correction algorithm boosts the correlation to beyond 0.83—even as high as 0.95 (Table 2)—in reasonable breathers (initial correlation > 0.5). Therefore, by using MR motion simulation and applying the phase-shift-estimation algorithms, patients can be categorized into 3 groups: (1) naturally high correlation, (2) enhanced high correlation, and (3) low correlation. Radiation-therapy planning and monitoring can thus be tailored to the patient's correlation group, bringing this modality one step closer to individualized treatment.

Recent reports suggest that patients' breathing irregularities may cause tumor underdosing when the internal tumor volume is used to plan the treatment.⁴⁰ Guidance for managing clinical motion is therefore urgently needed. Further study of the external-internal motion relationship and tumor-motion monitoring during treatment will thus be critical for improving the accuracy and outcomes of existing therapeutic strategies.

Conclusions

Significantly enhanced correlation between the movement of external and internal structures during free breathing has been achieved by correcting a patient-specific phase shift. Three phase-domain methods were developed to dynamically estimate the phase shift, and a more robust technique was realized by combining these individual methods. The value of the phase shift tends to be stable over 6 to 15 minutes, and possibly longer, suggesting that the phase shift can be determined and corrected immediately before treatment and periodically monitored for changes. Employing the phase-space technique to boost the external-internal motion correlation thus offers a promising strategy for guiding respiratory-gated radiation therapy.