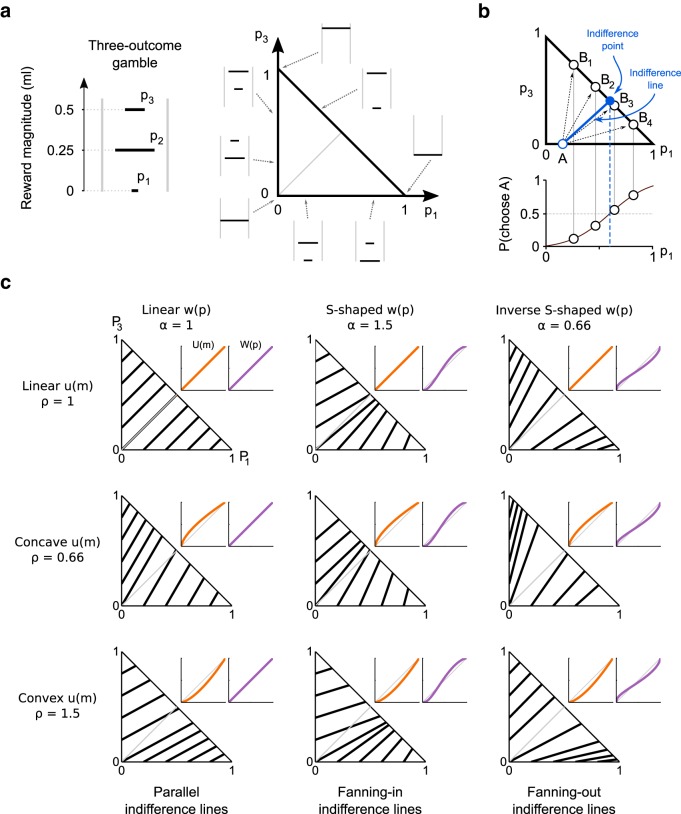
Figure 5.

Indifference lines in the Marschak–Machina triangle modeling different patterns of probability distortion. a, Representation of gambles in the Marschak–Machina triangle. Schematic representation of a three-outcome gamble (left): probabilistic combination (p₁, p₂, p₃) of three fixed magnitudes (m₁ = 0 ml, m₂ = 0.25 ml, m₃ = 0.50 ml), which can be represented in the Marschak–Machina triangle (right, with example gambles corresponding to points on the triangle edges). Gray line in triangle connects points with equal EV (0.25 ml). b, Procedure for the psychometric measurement of one indifference line. An indifference point (top, blue dot) in choices between a fixed gamble A and different gambles B_i (circles) was defined as the point on the triangle hypotenuse for which a softmax function fitted on the ratio of A over B_i choices equated 0.5 (bottom). An indifference line was then constructed by connecting such indifference point on the hypotenuse to the fixed gamble A (blue line). c, Theoretical indifference lines. Indifference lines predicted by cumulative prospect theory, for different underlying shapes of utility (u(m), power function) and probability distortion (w(p), Prelec-1 function). Each plot represents the indifference lines corresponding to a particular combination of u and w shapes, represented by orange and purple lines, respectively. The shape of the utility function (linear in the first row of plots, concave and convex in the other two rows) changes the global orientation of the indifference lines, without affecting their fanning direction. On the contrary, a change in probability distortion shape corresponds to a change in the fanning direction of indifference lines: a linear probability distortion (first column) produces parallel indifference lines, whereas S-shaped (second column) and inverse S-shaped (third column) probability distortions correspond to indifference lines fanning-in and fanning-out, respectively, regardless of the utility function shape.