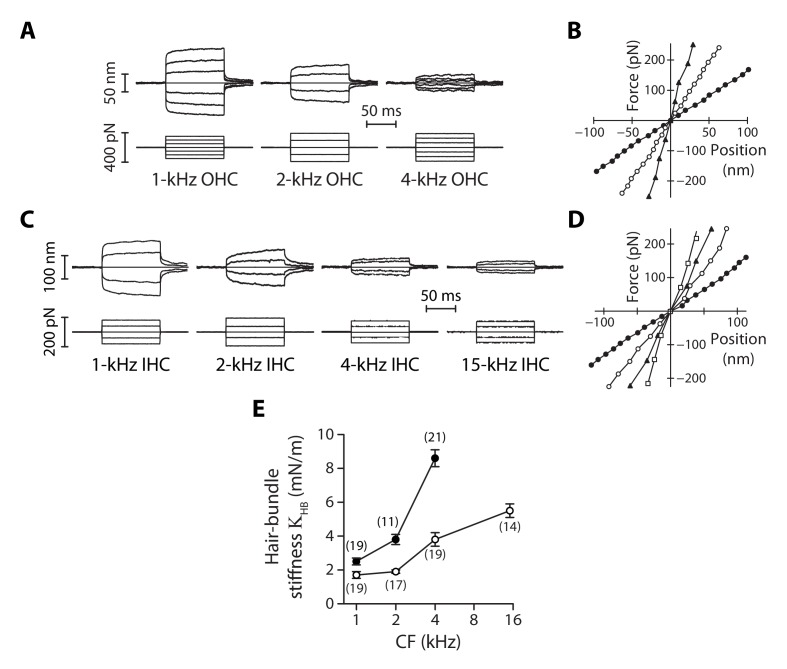
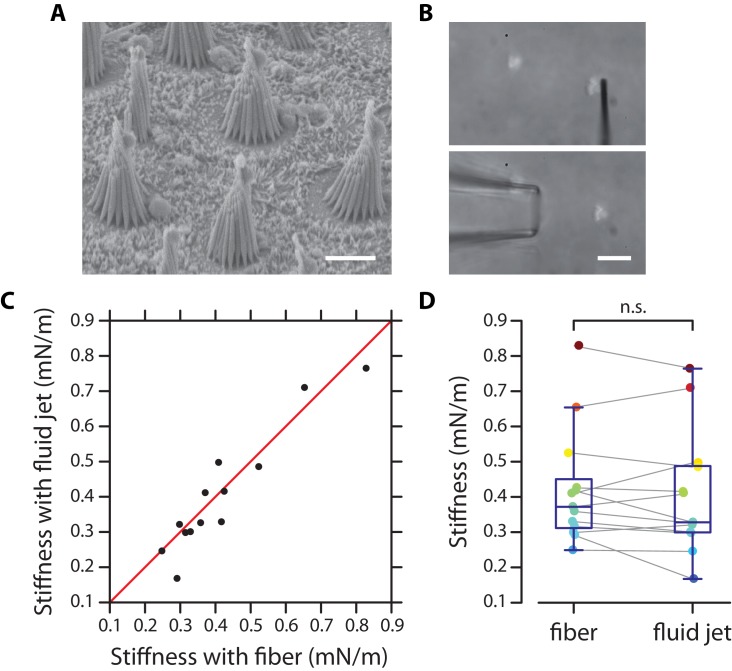
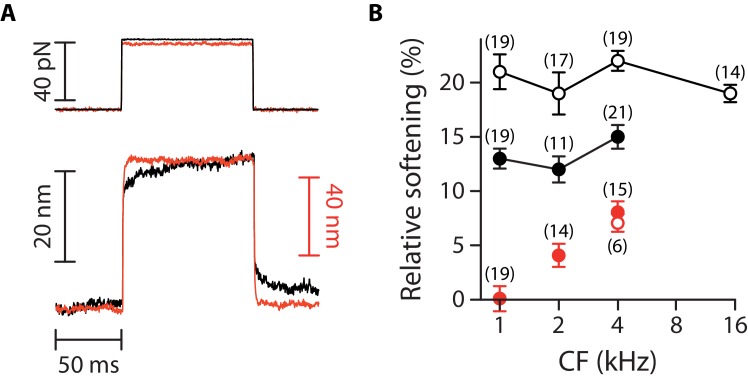
Figure 2. Stiffness gradients of the hair bundle.

(A) Hair-bundle movements (top) in response to a series of force steps (bottom) for outer hair cells (OHC) with characteristic frequencies of 1, 2, and 4 kHz (from left to right). (B) Force-displacement relations for the data shown in (A), with black disks, white disks and black triangles corresponding to characteristic frequencies of 1, 2, and 4 kHz, respectively. (C) Hair-bundle movements (top) in response to a series of force steps (bottom) for inner hair cells (IHC) with characteristic frequencies of 1, 2, 4, and 15 kHz. (D) Force-displacement relations for the data shown in (C), with black disks, white disks, black triangles, and white squares corresponding to characteristic frequencies of 1, 2, 4, and 15 kHz, respectively. (E) Stiffness (${\mathrm{{\rm K}}}_{\mathrm{H}\mathrm{B}}$) of a hair bundle under control conditions as a function of the characteristic frequency (CF) for inner (white disks) and outer (black disks) hair cells. Each data point in (E) is the mean ± standard error of the mean (SEM) with the number of cells indicated between brackets.

Figure 2—figure supplement 1. Velocity field of a fluid jet.

(A) Micrograph showing 200-nm beads entrained by a fluid jet; the beads were used as tracers for velocimetry. The dotted lines delimit the fluid cone coming out of the pipette; its half-aperture $\mathrm{\alpha }=$ 30° was in agreement with that measured with Coomassie blue (Figure 2—figure supplement 2), considering that the diameter of the fluid-jet pipette was here 10 μm. A scaled picture of an outer hair-cell bundle was inserted in the micrograph to illustrate how a hair bundle was positioned within the fluid jet. A movie was recorded with a high-speed camera (Photron Fastcam Mini UX50) at 5000 images/s. The position of the beads was automatically tracked in the $XY$ plane using the TrackMate plugin (Tinevez et al., 2017) of the image-processing software Image J (National Institute of Health, Bethesda, USA). (B) Longitudinal-velocity profile $v_X\left(x,y\right)$ along the transverse $Y$ axis, at several values of the distance $x$ from the pipette mouth along the $X$ axis. The data were well described by the function $v_X\left(x,y\right)=V_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(x\right)/{(1+{\left(y/A\left(x\right)\right)}^2)}^2$ (solid lines). The shaded area indicates the width of a hair bundle. We noticed that the half-aperture $\alpha$ of the fluid jet that we measured with Coomassie blue (Figure 2—figure supplement 2) or with the beads (A) was well approximated by ${\displaystyle \alpha \cong \overline{\alpha }={\tan }^{-1}\left(\left(A\left(x\right)-D_{\mathrm{F}\mathrm{J}}/2\right)/x\right)}$, where $D_{\mathrm{F}\mathrm{J}}$ is the diameter of the pipette; the oblique lines shown in the figure delimit the fluid jet and match the cone shown in (A). As a result, when a calibration fiber was placed perpendicular to the fluid jet (Figure 2—figure supplement 2B), the fiber experienced viscous drag over a typical length $L\left(x\right)\cong 2A\left(x\right)$. (C) The same velocity profiles as those shown in (B) are here overlapped; different symbols correspond to beads at different distances ${\displaystyle x}$ from the mouth of the fluid-jet pipette, according to the legend shown in (B). (D) Fluid velocity at $y=0$ as a function of the distance $x$. The data was well described by $v_X\left(x,0\right)=V_0/x$, with $V_0=$ 42 mm/s (solid line). (E) Fit parameters $V_{\mathrm{m}\mathrm{a}\mathrm{x}}\left(x\right)$ and $A\left(x\right)$ for the fits shown in (B and C) as solid lines, as well as the approximation for the fluid-jet half aperture ${\displaystyle \overline{\alpha }\left(x\right)}$.

Figure 2—figure supplement 2. Geometrical characteristics of a fluid jet.

(A) Visualization of a fluid jet using a solution containing a dye (Coomassie Brilliant Blue). To enhance contrast, a background image was recorded in the absence of the fluid-jet pipette and subtracted to the image of the fluid jet, resulting in the image shown here. The angle between the horizontal axis and the edge of the cone defines the half-aperture of the cone, noted $\mathrm{\alpha }$. Command voltage of −60 V. (B) Schematic representation of a calibration fiber intersecting a fluid jet over a length ${\displaystyle L=D_{\mathrm{F}\mathrm{J}}+2\mathit{x}\tan \alpha }$, in which ${\displaystyle D_{\mathrm{F}\mathrm{J}}}$ is the diameter of the pipette, $x$ is the distance from the pipette to the fibre and $\mathrm{\alpha }$ is the half-aperture of the fluid jet, as defined in (A). This length ${\displaystyle L}$ and the diameter ${\displaystyle D_{\mathrm{F}}}$ of the cylindrical fiber is used to calculate the effective hydrodynamic radius of the fiber (see Materials and methods in the main text). (C) Half-aperture $\mathrm{\alpha }$ as a function of the command voltage to the fluid-jet device, for pipette diameters ranging between 3–5 µm (light gray circles; n = 3), 5–7 µm (gray triangles; n = 5) and 7–9 µm (black squares; n = 3). Error bars correspond to mean values ± SEM. In practice, the maximal command voltage that we used to probe hair-bundle stiffness was 4 ± 0.3 V (mean ± SEM; n = 139). Over this range, the half-aperture of the fluid jet was nearly constant. We took a value of 22° for pipettes with a diameter of 3–5 µm and of 27° for pipettes with a diameter of 5–9µm.

Figure 2—figure supplement 3. Rise time and linearity of the fluid-jet stimulus.

(A) Deflection of a flexible fiber (bottom) in response to a series of command-voltage steps (top) applied to the fluid-jet device. (B) The time course of fiber deflection was well described by a single exponential (red line) with a time constant of 155 µs, corresponding to a rise time (5–95%) of 465 µs. This time constant was set by the relaxation time ${\displaystyle {\tau }_{\mathrm{F}}={\lambda }_{\mathrm{F}}/k_{\mathrm{F}}=}$ 160 µs of the fiber, in which k_F = 1.1 mN/m and λ_F = 173 nN·s/m were the stiffness and friction coefficient of the fiber, respectively. (C) Force on the fiber as a function of the command voltage to the fluid jet. The slope of the linear relation (linear fit in red) provided the calibration constant $C$, here $C=$ 42 pN/V. Same data as in (A and B).

Figure 2—figure supplement 4. Test of fluid-jet calibration in the frog’s sacculus.

(A) Electron micrograph of hair bundles from a sacculus of the frog (strain ‘Rivan92’ of Rana ridibunda). (B) Micrograph of a hair bundle ready to be stimulated by a flexible fiber (top) or by a fluid jet (bottom). (C) The stiffness estimated from fluid-jet stimulation is here plotted as a function of that estimated from fiber stimulation for a sample of 13 hair bundles. The red line has a slope unity. (D) The same data as that shown in (C) is represented here as box plots on top of the data points for each method of mechanical stimulation. Grey lines connect stiffness estimates for the same hair bundles. The mean values of both distributions, 0.40 ± 0.17 mN/m (mean ± SD; median: 0.33 mN/m) and 0.42 ± 0.16 mN/m (mean ± SD; median: 0.37 mN/m) for fluid-jet stimulation and fiber stimulation, respectively, are not statistically different (paired-sample t-test). Scale bars in (A–B) 5 µm.

Figure 2—figure supplement 5. Mechanical creep during a force step.

(A) Hair-bundle displacement (bottom) in response to a force step (top) before (black) and after (red) tip-link disruption, here for two different outer hair cells at the same cochlear location. With intact tip links (black), the hair bundles showed a mechanical creep corresponding to a motion in the direction of the applied force over the duration of the stimulus. Remarkably, the mechanical creep was abolished by tip-link disruption (red), suggesting that the creep was associated with mechanical adaptation (Hudspeth and Gillespie, 1994). (B) Relative softening $\left(K_1-K_2\right)/K_1$ associated with the mechanical creep for inner (circles) and outer (disks) hair cells before (black) and after (red) tip-link disruption. Here, ${\mathrm{{\rm K}}}_1$ and ${\mathrm{{\rm K}}}_2$ correspond to the hair-bundle stiffness measured 5–10 ms and 70–90 ms after the onset of the force step, respectively. To disrupt the tip links, the hair cells were here immersed for 15 min in a standard saline supplemented with 5-mM EDTA. The mechanical responses were then measured in standard saline. Error bars correspond to mean values ± SEM, with the number of cells indicated on the figure.