Abstract
The derivation of atomic polarizabilities for polarizable force field development has been a long standing problem. Atomic polarizabilities were often refined manually starting from tabulated values, rendering an automated assignment of parameters difficult and hampering reproducibility and transferability of the obtained values. To overcome this, we trained both a linear increment scheme and a multilayer perceptron neural network on a large number of high-quality quantum mechanical atomic polarizabilities and partial atomic charges, where only the type of each atom and its connectivity were used as input. The predicted atomic polarizabilities and charges had average errors of 0.023 Å3 and 0.019 e using the neural net, and 0.063 Å3 and 0.069 e using the simple increment scheme, respectively. As the algorithm relies only on the connectivities of the atoms within a molecule, thus omitting dependencies on the three-dimensional conformation, the approach naturally assigns like charges and polarizabilities to symmetrical groups. Accordingly, a convenient utility is presented for generating the partial atomic charges and atomic polarizabilities for organic molecules as needed in polarizable force field development.
Graphical Abstract
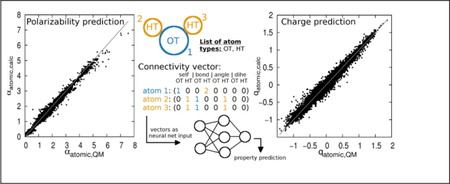
Large size quantum-mechanical calculations are utilized to predict partial charges and atomic polarizabilities to be used in force field development.
1. Introduction
Molecular dynamics (MD) simulation has been used for decades to explore chemical and biochemical problems, and greatly contributed to the current understanding of soft matter. Predominantly, additive (nonpolarizable) force fields have been used to describe the Hamiltonian of a system, disregarding the explicit treatment of electronic polarizability which is required to change the molecular dipole moments as the polarity of the environment varies. Consequently, the description of phenomena such as molecules passing through a membrane or the folding of proteins was limited. Progress has been made to overcome this limitation through the introduction of explicit induced polarization to force fields, where polarization has been treated on the basis of classical Drude oscillators,1–3 fluctuating charges4 or induced atomic dipoles.5,6 The addition of polarizability was shown to improve agreement with experiment for a number of systems, for example for helix formation7 or DNA-ion interactions.8–10 Polarizable force fields are furthermore important for systems with high Coulomb forces, such as ionic liquids, where the inclusion of polarizability led to better agreement to experiments of dielectric spectra, conductivities and time-dependent fluorescence.11–13
Within the classical Drude oscillator model,14 parameters for a range of biomolecules, small organic molecules and atomic ions are available (see Ref. 1 and references therein). However, the chemical space of small organic, drug-like molecules is vast, and the current parametrization strategy is very tedious and time demanding. 1 Towards overcoming this an automated procedure to obtain parameters was proposed for the AMOEBA polarizable force field, operating on induced dipoles. 15 In addition, the General Automated Atomic Model Parameterization (GAAMP)16 can refine previously obtained force field parameters for polarizable Drude force fields using quantum mechanical (QM) calculations as target data. However, due to the necessity to conduct multiple QM calculations for each molecule, these approaches are time consuming such that these tools do not yet represent a general force field.
In contrast, a number of general nonpolarizable force fields exist, such as the CHARMM general force field (CGenFF),17–19 the general Amber force field (GAFF),20 the OPLS all-atom force field (OPLS-AA)21,22 and the Merck molecular force field (MMFF).23–25 With these force fields and associated tools, it is possible to rapidly generate topologies and parameters for a large range of organic, drug-like compounds. Notably, CGenFF and MMFF involve algorithms that totally avoid the need to perform QM calculations during generation of the electrostatic parameters. For polarizable force fields to move into areas like drug discovery or the design of ionic liquids similar tools will be required. However, the development of such tools in the context of a general polarizable force field is challenging as it requires algorithms to predict the required electrostatic parameters, including partial atomic charges, atomic polarizabilities, anisotropic polarizabilies, Thole scale factors and lonepairs as well as bonded and van der Waals parameters.
Towards this goal we present a parameter estimation tool delivering ab-initio quality partial charges and atomic polarizabilities in a rapid fashion. The approach builds on approaches that exist for the prediction of partial charges17,26–28 through the calculation of atomic polarizabilities and partial atomic charges using QM-based methods to produce a large training set as required for optimization of rapid parameter estimation schemes. While QM calculation of atomic polarizabilities for neutral compounds has been known for some years,29–32 the description of charged species has been found only recently.33,34 This new approach allows for the rapid estimation of atomic polarizabilities that may be combined with known approaches for the determination of partial atomic charges. Taking advantage of this, in the present study we conducted QM calculations of atomic polarizabilities of 11500 molecules with a high model chemistry (MP2 with Sadlej’s polarizable PVTZ basis set35). Partial charges were obtained by two stage restricted electrostatic potential (RESP) fitting36,37 using the same model chemistry. The resulting atomic electrostatic parameters were then used to train both a linear increment scheme, as well as a neural network to predict polarizabilities and charges depending on the identity of an atom and that of its neighboring atoms. Furthermore, lone pairs and anisotropies were set up based on the atomic connectivities, consistent with the Drude-polarizable force field. Thus, we present a powerful prediction tool of electrostatic parameters to be used in Drude polarizable force fields. Importantly, this represents a significant step towards a Drude general force field (DGenFF) in analogy to the current additive CGenFF.
2. Computational Details
2.1. Atom-type based structure identifiers
To describe the identity of an atom and its surrounding structure, vectors containing the connectivity or distance information were calculated for each atom. Both approaches make use of the 157 CGenFF17 atom types, but process the relevant data differently.
The connectivity vectors hold information about the atom identity and neighboring atoms connected via no more than three edges. Each vector is a row vector of length 628 and contains only integer numbers. The first 157 values hold information about the atom identity, i.e. the value 1 in the column corresponding to the respective atom type and 0 in all other columns (often referred to as one-hot encoding). Bond information is stored in the second set of 157 columns, where the value in the column for type A is increased by 1 if the atom is bonded to an atom of type A (connected via one edge). The third and fourth set of 157 columns correspond to angles and dihedrals in analogy to the bond section (connections via two or three edges).
The distance vectors are row vectors of length 942 and also contain only integer numbers, where distance information was extracted from the optimized QM geometries (MP2/6–31+G(d)). Each atom type corresponds to six columns in the vector, depending on the distance of the atom to the point of interest. All possible distances are reduced to six bins, [0,0.5], [0.5,1.5], [1.5,2.5], [2.5,3.5], [3.5,4.5], [4.5,5.5] in units of Å. For each atom the distance vector arises by calculating the distances to all other atoms, and counting their occurrence with respect to distance and atom type. The atom type of the atom itself is also taken into account and added to the [0,0.5] bin. An example of the respective connectivity and distance vectors of a water molecule is given in Fig. 1.
Figure 1:
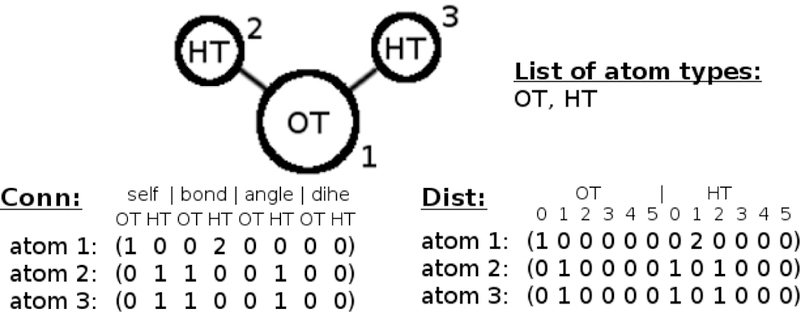
Exemplary connectivity (‘Conn’) and distance (‘Dist’) vectors of a water molecule, if the complete atom type list consists of only the two fictitious types ‘OT’ and ‘HT’. During this work, a list of 157 atom types was used, similar to CGenFF. The numbers above each row in the distance scheme correspond to the respective bins (i.e. 0 corresponds to the bin [0,0.5[, 1 to [0.5,1.5[ Å).
2.2. Training and test set
Atomic polarizabilities and partial charges of 189774 atoms in 11500 small molecules (containing no more than 30 atoms) were calculated via quantum mechanics using the program package Psi4.38 10000 molecules from the ZINC fragment-like database39 served as a training set for different algorithms predicting atomic polarizabilities and charges. The training set was selected to cover a broad range of functionalities, structure elements and atom types. To perform this the CGenFF program17 was run on all molecules from the ZINC database containing no more than 30 atoms to assign the atom types of about half a million molecules from which the corresponding connectivity structure vectors, Xi, were constructed as described above. Fig. 2 depicts how 10000 molecules were chosen from the database based on their atom types. First, all molecules with no more than ten atoms were chosen, and their connectivity vectors were summed up. Then, new molecules were chosen iteratively to increase the lowest values in the cumulative structure vector. In practice, molecules that contained a non-zero entry in the lowest value column of the cumulative vector were iteratively added to the training set.
Figure 2:
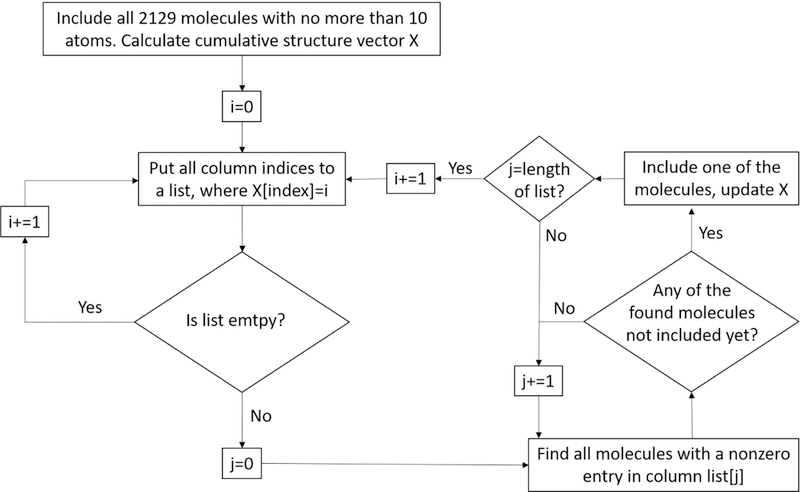
Algorithm used for selection of fragment molecules from ZINC with maximal coverage of chemical functional groups. All molecules with no more than 10 atoms were included in the training set. Then, molecules larger than 10, but smaller than 30 atoms were selected iteratively according to underrepresented structure elements. First, all structure elements which are not present (i = 0) were put into a list of length j, then one new molecule was selected per structure element in the list, if possible. Next, structure elements which occured only once (i = 1) were put into a list, and new molecules matching those structure elements added accordingly. Thus, in each iteration i was increased by 1, column indices where X[index] = i put to a list of length j, and molecules added. The algorithm was halted after 10000 molecules were chosen.
Additionally, 1500 molecules commonly used in molecular dynamics simulation served as an independent test set, and were used to estimate average errors of the polarizability and charge predictions. 430 molecules were taken from CGenFF17 (set A), 89 from the database of ring structures from Ref. 40 (set B), 395 from the database of Ref. 41 (set C) and 586 from the FreeSolv database42 containing water-soluble neutral molecules (set D).
2.3. Quantum mechanical calculation of partial charges and polarizabilities
The geometries of all molecules were optimized at a MP2/6–31+G(d) model chemistry. Partial charges at the optimized geometries were obtained by two stage restricted electrostatic potential (RESP) fitting36,37 at the MP2/Sadlej35 model chemistry. During the first stage, the electrostatic potential was fitted in the presence of a weak hyperbolic restraint towards zero, leading to small charges at buried sites (in contrast to conventional ESP fitting). During the second stage the partial charges were refitted to force equal charges on hydrogen atoms connected to the same carbon atom, with a stronger hyperbolic constraint towards zero. This charge redistribution only affects carbons attached to hydrogens, as well as the respective hydrogens, and does not change the assigned partial charges to polar moieties such as hydroxyl or carbonyl groups. The hyperbolic form of the penalty function is , with qj being the partial charge of atom j. The strength of the restraint is given by a and was set to 0.0005 au or 0.001 au for the weak and strong restraint respectively. The parameter b corresponds to the tightness of the hyperbola at values close to zero and was set to 0.1 au. The values were chosen according to Ref. 36. The electrostatic potential was calculated on four surfaces at 1.4, 1.6, 1.8 and 2.0 times the van-der-Waals radii. The grid density was set to 20 points per Å2.
In addition to the single point calculation for the RESP fitting, six single point energy calculations (MP2/Sadlej) at electric dipole fields of 0.0008 au in the positive and negative x, y and z direction were conducted and the resulting wave functions saved. The change in the electron distribution with an applied electric field gives rise to the atomic polarizabilities, using the post-processing scripts published in Ref. 32,33. In short, the components of the atomic polarizability tensor αi of an atom i can be computed as the first derivative of the atomic dipole moment μi with respect to the electric field F as
| (1) |
with a and b denoting the x, y and z directions. The origin independent atomic dipole moment μi of the non-overlapping atomic integration basin Ωi at the atomic site i at coordinates Ri is defined as
| (2) |
where i is bonded to Nb sites j. The bond charge qb(ij) is the contribution of the directed bond between i and j to the net partial charge of atom i. Rb(ij) denotes the coordinates of the bond charge (this can be set to (Ri + Rj)/2). The polarization of the electron cloud around the nucleus, μip, was obtained from the GDMA code of Misquitta and Stone,43,44 where multipoles of order 1 (dipoles) were calculated for each atomic site. The contribution of charge transfer to the dipole moment, μic, was obtained from the charges and coordinates of each atomic site, where the bond charges qb(ij) arise from the GDMA net atomic charges qi by solving the set of equations
| (3) |
| (4) |
| (5) |
2.4. Training of linear polarizability and charge increments
The training algorithm is based on a least-squares linear algebra solver. Using the atomic polarizabilities, charges and structure information of each atom in each molecule, a large set of linear equations is set up
| (6) |
| (7) |
where refers to the QM atomic polarizabilities, and to the QM partial charges. The matrix X is of size n x m and contains the structure vectors of all n atoms in the training set. Either the connectivity information can be used, where m is 628, or the distance information, where m equals 942. For either of the two approaches X contains information about the identity and surrounding of each atom in the database. The vectors and hold m polarizability and charge increments, respectively. The set of equations is solved for and . Using the connectivity matrix the general identity, bond, angle and dihedral increments are obtained, whereas using the distance matrix increments depending on the atom type and distance to the central atom are obtained, disregarding the connectivity. Both can be utilized to predict polarizabilities and charges of new molecules.
2.5. Machine learning approach to predict polarizabilities and charges
In addition to the linear model, the connectivity based structural vectors were also utilized as input vectors for machine learning. In preliminary investigations, gradient tree boosting45 and multilayer perceptron neural net46–48 approaches were applied and compared. Twenty percent of the training set examples were split off and used as a validation set in order to estimate the methods performance on data the algorithm was not trained on. After initial hyperparameter49 tuning, both methods yielded remarkably comparable mean absolute errors; however the neural net approach tended to produce lower magnitude outliers. Thus, the neural net approach was opted as the method of choice.
Development of the neural net model was performed as follows. The loss function50 was chosen as the mean square error (L2-norm) with no activation function46,47 in the output layer. Xavier uniform initialization51 was applied to the weights and biases. In order to elaborate reasonable boundaries, the hyperparameter space was initially explored manually. To prevent overfitting,46,52 L2-regularization as well as dropout were tested, with neither yielding a beneficial effect. Using the obtained boundary knowledge, grid search using 3-fold cross-validation53 was performed. The Adam optimizer54 was used with initial learning rates 5 ✻ 10−3, 10−3 and 5 ✻ 10−4. Values 0.9 and 0.999 were chosen for the first and second momentum, respectively, 10−8 as the numerical stability parameter. Hidden Layer sizes of 256, 512, 1024 and 2048 neurons as well as two consecutive and three consecutive 1024 neuron layers were tested. Early stopping on the validation set with a maximum of 100, 250 and 500 epochs as well as training up to the according full number of epochs was explored. The performance of tangens hyperbolicus, rectified linear unit (ReLU, also known as rectification nonlinearity)55 and exponential linear unit (ELU)56 activation functions was probed. Minibatch sizes of 256, 512 and 4096 were included in the grid search. Minimum maximum feature rescaling to the interval [0,1] was applied.
With respect to the mean absolute error as well as the maximum error across the training set, the following setup was chosen for production. Three consecutive 1024 neuron hidden layers were employed. The ReLU activation function was used. For each gradient step, shuffled minibatches of size 256 and 512 were chosen for charge and polarizability predictions, respectively. Training was performed for 250 epochs using a learning rate of 5 ✻ 10−4.
3. Results
Quantum mechanical atomic polarizabilities and RESP partial charges were calculated for all 11500 molecules (training set, and test sets A to D) using a high model chemistry: MP2/Sadlej. For each atom the connectivity and distance structure vectors were calculated, based on the CGenFF atom types of the atom itself and the neighboring atoms connected via no more than three edges (connectivity scheme) or up to a distance of 5.5 Å (distance scheme). Distances were calculated on the single, QM minimized geometry obtained for each molecule. The obtained information of the training set (10000 molecules) was fed to either a linear regression or a machine learning algorithm to relate the structure vectors to the QM polarizabilities and charges. Thus, the trained increment or neural net algorithm can be used to predict polarizabilities and charges without the necessity of conducting QM calculations. To test the performance of the different algorithms on molecules they were not trained on, the QM values of the four independent test sets were compared to the respective predictions. In the following, we describe the results obtained by the linear increment approach and the multilayer perceptron neural network in detail.
3.1. Linear increments
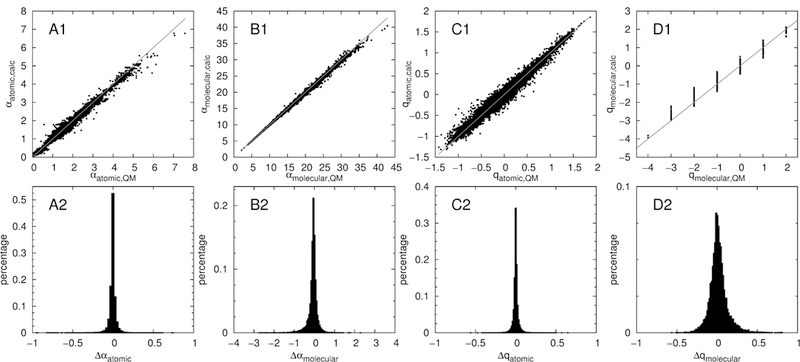
Linear, additive increments based on the connectivity information were obtained by solving Eq. (6) and (7) for all 166056 atoms in the training set containing 10000 molecules from the ZINC database. A R2 of 0.975 was obtained for the regression of polarizability values, and 0.919 for the corresponding partial charges. A comparison of the predicted values against the QM target data is shown in Fig. 3. Overall, the fit is very good, despite some outliers, which are discussed in the following. Polarizability predictions for molecules containing the atom types SG302, SG2D1, CG2D2O, CG2DC1 or CG2DC2 (gray dots in Fig. 3) were found to be problematic. The sulfur types correspond to thiolates and thiocarbonyls and show a wide variety of polarizabilities in QM. Large changes in polarizability were observed depending on the structure of the molecule, especially if the molecule can redistribute charge from the sulfur atom to the rest of the molecule through resonance. However, the increment scheme assigned only a narrow range of polarizabilities for the two sulfur types, which reflects a natural limitation of atom types and their inability to describe resonance effects. The carbon types correspond to conjugated double bonds. Large conjugated systems lead to large charge transfer contributions to the polarizability, which are underestimated by the prediction algorithm. The increment scheme takes into account structure information only up to three edges away from the atom of interest, and thus has no information about the actual length of a conjugated system. Since large polarizabilities caused by charge transfer are not desirable for the use in Drude force fields (where charge transfer is not possible), this error is of minor importance.
Figure 3:
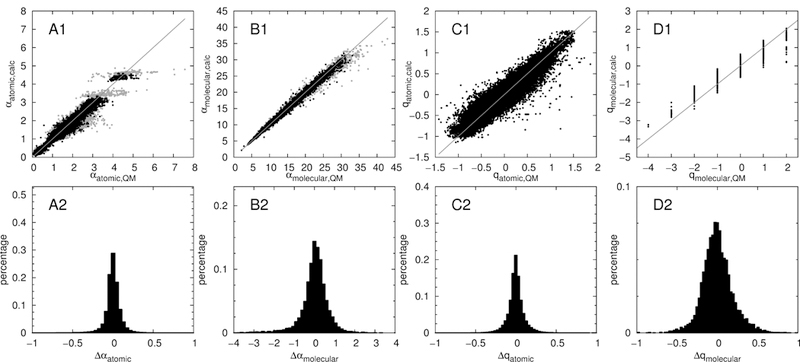
Comparison of connectivity increment scheme (IC conn) predicted atomic (A) and molecular (B) polarizabilities, as well as atomic (C) and molecular (D) charges to the respective QM values. Top: direct comparison to QM. Bottom: histogram of the respective deviations. Gray dots indicate atom types SG302, SG2D1, CG2D2O, CG2DC1 or CG2DC2
The charge increment predictions fit the QM charges well, except for carbon atoms next to highly charged moieties, e.g. bonded to two phosphates. Average atomic and molecular deviations for both the polarizabilities (Δα) and the partial charges (Δq) are listed in the first rows of Table 1 (labeled ‘IC conn.’). The average error of the predicted atomic polarizabilities is only 0.063 Å3 while for molecular polarizabilities the average error is 0.47 Å3. The low deviation of the predicted molecular polarizabilities from their QM counterpart is especially noteworthy, since the algorithm never trains on the overall molecular polarizabilities, but only on atomic polarizabilities. The deviations of the predicted charges are also quite low, 0.069 e for the directly predicted charges, 0.068 e after correction of the overall charge, and 0.14e for the summed up (uncorrected) charges.
Table 1:
Average errors in atomic () and molecular () polarizability, as well as atomic (), corrected atomic () and molecular () charges. ’IC conn.’ refers to the increment scheme based on connectivities, ’IC dist.’ to the increment scheme based on distance bins, and ’ML conn.’ to the neural net using the connectivity vectors as inputs.
| [Å3] | [Å3] | [e] | [e] | [e] | ||
|---|---|---|---|---|---|---|
| IC conn. | training set | 0.063 | 0.47 | 0.069 | 0.068 | 0.14 |
| set A | 0.051 | 0.44 | 0.061 | 0.060 | 0.11 | |
| set B | 0.053 | 0.40 | 0.051 | 0.051 | 0.09 | |
| set C | 0.036 | 0.28 | 0.049 | 0.049 | 0.07 | |
| set D | 0.043 | 0.36 | 0.053 | 0.053 | 0.09 | |
| IC dist. | training Set | 0.064 | 0.44 | 0.076 | 0.075 | 0.15 |
| set A | 0.051 | 0.36 | 0.068 | 0.067 | 0.14 | |
| set B | 0.054 | 0.33 | 0.060 | 0.059 | 0.13 | |
| set C | 0.042 | 0.23 | 0.065 | 0.064 | 0.14 | |
| set D | 0.046 | 0.31 | 0.064 | 0.065 | 0.18 | |
| ML conn. | training set | 0.023 | 0.15 | 0.019 | 0.019 | 0.08 |
| set A | 0.035 | 0.27 | 0.042 | 0.041 | 0.13 | |
| set B | 0.033 | 0.26 | 0.038 | 0.037 | 0.13 | |
| set C | 0.028 | 0.20 | 0.033 | 0.033 | 0.11 | |
| set D | 0.030 | 0.26 | 0.037 | 0.036 | 0.13 | |
Using the trained polarizability and charge increments, the electrostatic parameters of sets A to D were calculated and compared to QM, shown in Fig. 4 and Table 1. The deviations are very low, even lower than the deviations within the training set itself. The reason behind this peculiar behavior is the vast diversity of the molecules in the training set, where some uncommon structures are not well described. In contrast, sets A to D contain biologically relevant small molecules showing quite simple, common structures, which can be predicted very well using the increment scheme.
Figure 4:
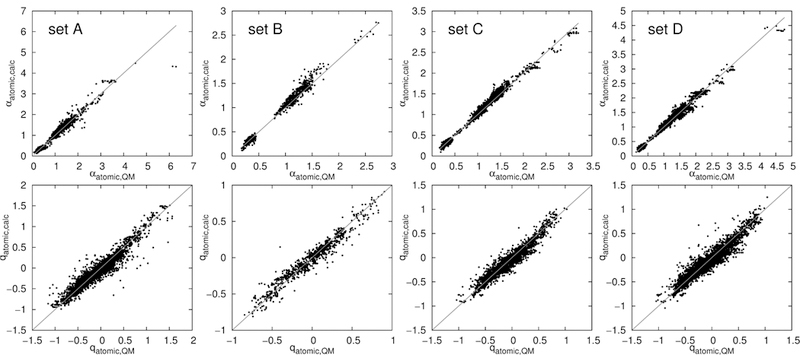
Predicted connectivity increment scheme (IC conn) atomic polarizabilities and charges of set A, B, C and D versus the QM values.
Table 1 also lists the average deviations of the predicted electrostatic parameters when trained on distance instead of connectivity data (rows labeled ‘IC dist.’). The obtained errors are nearly the same as in the connectivity increment algorithm, offering no general advantage, even despite the larger number of variables. Furthermore, the problematic atom types discussed above remain problematic, producing similar errors (data not shown). A R2 of 0.976 for polarizabilities, and 0.907 for partial charges was obtained. Thus, the description of the structure via distance is comparable, and for some cases even inferior, to a connectivity-based algorithm. Furthermore, as distance-based estimations are sensitive to the three-dimensional structure of the molecules, they are not appropriate for use in force fields since the electrostatic parameters cannot change as a function of conformation. Thus, the remainder of this study focuses only on structure identifiers via connectivities.
3.2. Multilayer perceptron neural net
Despite the somewhat surprising general accuracy of the linear polarizability and charge increment scheme for molecules with simple, common structures, the linear scheme fails to describe nonlinear effects. For example, the nitrogen in S(−)-CH=N-R increases the polarizability of sulfur by a specific value, (namely its angle increment), without taking into account that such a structure could redistribute charge from sulfur to nitrogen, thus lowering the polarizability of sulfur. This is due to the increment scheme not taking into account the nature of the bridging atom in the angle increments, such that it uses the same angle increment for each specific pair of atom types separated by two edges, without connecting the information encoded in the respective atom types any further. A neural network, in contrast, connects all the information contained in the input vector, and is thus capable of detecting interrelations of specific atom types connected via a specific number of bonds. Indeed, the trained neural net removes most of the outliers seen in the linear increment scheme and lowers the mean absolute deviations to the QM data substantially. In Fig. 5, the atomic and molecular polarizabilities and charges predicted from the neural net are plotted versus the respective QM values. Furthermore, histograms of the deviations are given. The algorithm is able to predict both polarizabilities and charges with mean absolute errors of 0.023 Å3 and 0.019 e respectively, thus outperforming the increment scheme. These mean absolute deviations to the QM training data are given in Table 1 (labeled ‘ML conn.’). The neural net also predicts the polarizabilities and charges of the test sets A to D well, although it was not trained on them. A plot of the predicted versus the QM polarizabilities and charges is shown in Fig. 6 for all four test sets. Deviations are listed in Table 1. Again, the deviations of the machine learning predictions to the QM values are lower than the respective deviations within the increment method. The neural net furthermore produces less outliers than the increment algorithm, as visible from Fig. 5 and Fig. 6. The atom types that were found to be problematic for the increment scheme are well described by the neural network. The multilayer perceptron neural net trained in this study is thus able to supply ab-initio quality atomic polarizabilities and partial charges for a wide variety of chemical compounds, without any severe outliers.
Figure 5:
Comparison of connectivity machine learning algorithm (ML Conn) predicted atomic (A) and molecular (B) polarizabilities, as well as atomic (C) and molecular (D) charges to the respective QM values. Top: direct comparison to QM. Bottom: histogram of the respective deviations.
Figure 6:
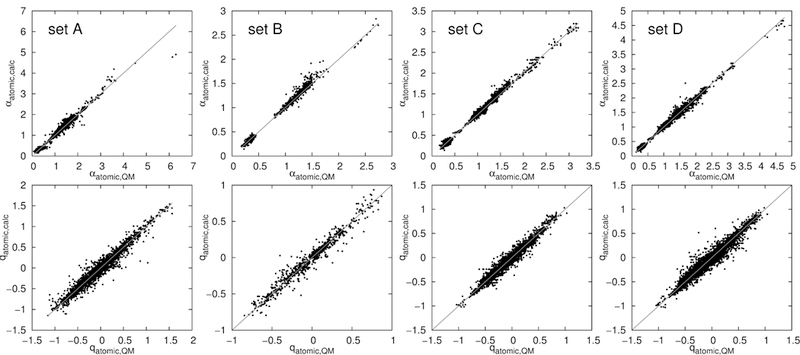
Connectivity machine learning algorithm (ML Conn) predicted atomic polarizabilities and charges of set A, B, C and D versus the QM values.
3.3. Prediction tool
To make the prediction algorithms available for a broader audience, a program was written in bash and python and can be downloaded from Ref. 57 or 58 free of charge together with instructions on how to use the script. It predicts atomic polarizabilities and partial charges via either the connectivity linear increment scheme or the neural net algorithm. As the predicted charges, q, typically do not add up to integers the prediction tool generates corrected charges (q’) that do. This is performed by distributing the net difference between the total charge summed over q with the expected integer charge over all atoms. For example if a 10 atom molecule has a net charge of 0.1 instead of 0, 0.01 will be subtracted from each partial charge, yielding q’. Furthermore, lonepair and anisotropy information is generated in analogy to the Drude Force Field. The program takes CGenFF combined topology and parameter files (str) as input, which can be generated from mol2 files using the CGenFF Program17 or online using the PARAMCHEM server. 18,19,59
4. Discussion
In the following we discuss the strengths and weaknesses of the employed algorithms, limitations, and potential improvements.
The linear increment scheme is able to predict atomic polarizabilities and charges well for most molecules, but fails to capture nonlinear effects, such as charge redistribution via resonance. It is nevertheless a simple and convenient scheme to quickly estimate polarizabilities and charges with low average errors, and can be used for molecules with simple, common structure elements, or whenever high precision is not necessary.
For molecules with more uncommon structures, or if more precise electrostatic parameters are needed we recommend to use the machine learning algorithm instead. It predicts accurate atomic polarizabilities and charges for all molecules in the training set, and performs well for the four test sets which contain molecules often used in MD simulations. Since the predicted electrostatic parameters are intended to serve as the basis for a general polarizable force field valid for a wide range of small molecules, generality and transferability of the parameters are essential. Too high precision, which is usually connected to high specificy at the cost of generality (overfitting), may therefore be counterproductive. However, the obtained magnitude of average error, namely errors in the second decimal for both polarizability and partial charges, are remarkably low, and should suffice for most applications. If more specific parameters for a molecule possessing very uncommon structure elements are needed, regular QM calculations should be conducted and the electrostatic parameters optimized following the published protocols. It is also for this reason that more neuron layers were not added to construct a deeper neural net as this may hamper the generality of the obtained parameters due to overfitting. Thus, we do not recommend increasing the size of the neural net without further increasing the training set.
A larger training set will furthermore reduce the dependence of the predicted parameters on the geometry. The prediction itself does not rely on the atomic coordinates of a molecule, but the QM data the models are trained on depends on conformation and geometry. While the atomic polarizabilities are largely independent of the three-dimensional structure of a molecule, the partial charges change to some extent.60,61 To prevent the trained model to indirectly rely on geometry due to the conformation dependence of the input vector, a sufficient size of the training set is indispensable. Thus, an atom with a specific structure vectors occurs in multiple molecules with different geometries. Since the training set already consists of about 166.000 atoms in 10.000 molecules, the presented predicted electrostatic parameters should be largely independent of geometry.
Last but not least, a general limitation of the presented method to predict polarizabilities and charges based on CGenFF atom types and connectivities lies in the atom types: If a molecule contains an atom that cannot be described within the CGenFF framework, the corresponding structure vector cannot be set up. In this case the user will again need to resort to QM calculations combined with the known parametrization strategies.
5. Conclusion
We have shown that breaking down the structure of a molecule into simple atomic fingerprints relying only on CGenFF atom types produces atomic structure vectors suitable for predicting atomic polarizabilities and partial atomic charges. Each atomic fingerprint holds the atom types of the corresponding atom and the respective connected atoms, here up to three edges. The structure vectors were used to train both a linear increment scheme (linear regression), as well as a machine learning algorithm (multilayer perceptron neural network). The increment scheme, where the properties of an atom are defined based on increments depending on the atom type of the atom itself and of the connected atoms, performs quite well, despite its simplicity. Low average errors of 0.063 Å3 for atomic polarizabilities and 0.069 e for partial charges prove that both polarizability and charge can be described quite well by additive contributions based on the local structure. However, the increment scheme suffers from outliers, which are low in number, but severe (errors up to 2 Å3). Poor predictions were in general observed whenever CGenFF atom types cannot account for resonance effects, or specific pairs of atom types influence each other in a specific way. Such nonlinear effects could be described by training a neural network on the QM atomic polarizabilities and charges, using the same structure vectors as used in the increment scheme as input. Thus, the outliers could be reduced to nearly zero, and the average errors lowered to 0.023 Å3 and 0.019 e, respectively. This is remarkable, since the input of both increment system and neural network are the same, and basically suffer from the same problems, i.e. where atom type and local connectivity cannot describe an atom sufficiently. Thus, using either the more elaborate neural net algorithm, or even the simple increment scheme, we can predict high-level ab-initio electrostatic properties by supplying only the connectivities of a molecule. In fact, training of the linear increment scheme based on geometry instead of connectivity via inclusion of the atom-atom distances did not lead to improved polarizability or charge predictions. Since the prediction routine is independent of the conformation of a molecule, the geometry does not need to be known, which decreases the workload of electrostatics parametrization of a new molecule considerably. Due to the large training set where each structure element occurs in multiple molecules in different conformations the predicted parameters do not depend largely on geometry, and are both general and transferable between different molecules. Both algorithms (linear increments, and neural net) are available free of charge, and come with a complete program processing the structure of a molecule, setting up the atomic structure vectors, and feeding them through the requested algorithm. Thus, an important step towards the automated setup of polarizable force fields within the Drude framework was accomplished.
Acknowledgement
The authors would like to thank Philipp Honegger for helpful discussions on the setup of neural networks. E.H. is recipient of a DOC Fellowship of the Austrian Academy of Sciences at the Institute of Computational Biological Chemistry. M.F. acknowledges funding from the Austrian Science Fund (P 31024). A.D.M. acknowledges support from the NIH (GM072558, GM070855 and GM051501).
Footnotes
Conflicts of interest
ADM Jr. is cofounder and CSO of SilcsBio LLC.
References
- (1).Lemkul JA; Huang J; Roux B; MacKerell AD Jr. An Empirical Polarizable Force Field Based on the Classical Drude Oscillator Model: Development History and Recent Applications. Chem. Rev 2016, 116, 4983–5013. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (2).Lamoureux G; MacKerell AD; Roux B A Simple Polarizable Model of Water Based on Classical Drude Oscillators. J. Chem. Phys 2003, 119, 5185–5197. [Google Scholar]
- (3).Lamoureux G; Roux B Modeling Induced Polarization with Classical Drude Oscillators: Theory and Molecular Dynamics Simulation Algorithm. J. Chem. Phys 2003, 119, 3025–3039. [Google Scholar]
- (4).Bauer BA; Patel S Recent Applications and Developments of Charge Equilibration Force Fields for Modeling Dynamical Charges in Classical Molecular Dynamics Simulation. Theor. Chem. Acc 2012, 131, 1153. [Google Scholar]
- (5).Wang ZX; Zhang W; Wu C; Lei HX; Cieplak P; Duan Y Strike a Balance: Optimization of Backbone Torsion Parameters of AMBER Polarizable Force Field for Simulations of Proteins and Peptides. J. Comput. Chem 2006, 27, 781–790. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (6).Wang J; Cieplak P; Li J; Wang J; Cai Q; Hsieh M-J; Lei H; Luo R; Duan Y Development of Polarizable Models for Molecular Mechanical Calculations: 2. Induced Dipole Models Significantly Improve Accuracy of Intermolecular Interaction Energies. J. Phys. Chem. B 2011, 115, 3100–3111. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (7).Huang J; MacKerell AD Jr. Induction of Peptide Bond Dipoles Drives Cooperative Helix Formation in the (AAQAA)3 Peptide. Biophys. J 2014, 107, 991–997. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (8).Savelyev A; MacKerell AD Jr. Differential Impact of the Monovalent Ions Li+, Na+, K+ and Rb+ on DNA Conformational Properties. J. Phys. Chem. Lett 2015, 6, 212–216. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (9).Savelyev A; MacKerell AD Jr. Competition among Li+, Na+, K+ and Rb+ Monovalent Ions for DNA in Molecular Dynamics Simulations Using the Additive CHARMM36 and Drude Polarizable Force Fields. J. Phys. Chem. B 2015, 119, 4428–4440. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (10).Savelyev A; MacKerell AD Jr. Differential Deformability of the DNA Minor Groove and Altered BI/BII Backbone Conformational Equilibrium by the Monovalent Ions Li+, Na+, K+ and Rb+ Via Water-Mediated Hydrogen Bonding. J. Chem. Theory Comput 2015, 11, 4473–4495. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (11).Heid E; Docampo-Alvarez B; Varela LM; Prosenz K; Steinhauser O; Schroder C Langevin Behavior of the Dielectric Decrement in Ionic Liquid Water Mixtures. Phys. Chem. Chem. Phys 2018, 20, 15106–15117. [DOI] [PubMed] [Google Scholar]
- (12).Schröder C; Sonnleitner T; Buchner R; Steinhauser O The Influence of Polarizabilty on the Dielectric Spectrum of the Ionic Liquid 1-Ethyl-3-methylimidazolium triflate. Phys. Chem. Chem. Phys 2011, 13, 12240–12248. [DOI] [PubMed] [Google Scholar]
- (13).Heid E; Schröder C Solvation Dynamics in Polar Solvents and Imidazolium Ionic Liquids: Failure of Linear Response Approximations. Phys. Chem. Chem. Phys 2018, 20, 5246–5255. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (14).Drude P; Millikan RA; Mann RC The Theory of Optics; Longmans, Green, and Co: New York, 1902. [Google Scholar]
- (15).Wu JC; Chattree G; Ren P Automation of AMOEBA Polarizable Force Field Parametrization for Small Molecules. Theor. Chem. Acc 2012, 131, 1138. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (16).Huang L; Roux B Automated Force Field Parametrization for Nonpolarizable and Polarizable Atomic Models Based on Ab Initio Target Data. J. Chem. Theory Comput 2013, 9, 3543–3556. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (17).Vanommeslaeghe K; Hatcher E; Acharya C; Kundu S; Zhong S; Shim J; Darian E; Guvench O; Lopes P; Vorobyov I; MacKerell AD Jr. CHARMM General Force Field: A Force field for Drug-Like Molecules Compatible with the CHARMM All-Atom Additive Biological Force Field. J. Comput. Chem 2010, 31, 671–690. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (18).Vanommeslaeghe K; MacKerell AD Jr. Automation of the CHARMM General Force Field (CGenFF) I: Bond Perception and Atom Typing. J. Chem. Inf. Model 2012, 52, 3144–3154. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (19).Vanommeslaeghe K; Raman EP; MacKerell AD Jr. Automation of the CHARMM General Force Field (CGenFF) II: Assignment of Bonded Parameters and Partial Atomic Charges. J. Chem. Inf. Model 2012, 52, 3155–3168. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (20).Wang J; Wolf RM; Caldwell JW; Kollman PA; Case DA Development and Testing of a General Amber Force Field. J. Comput. Chem 2004, 25, 1157–1174. [DOI] [PubMed] [Google Scholar]
- (21).Jorgensen WL; Maxwell DS; Tirado-Rives J Developement and Testing of the OPLS All-Atom Force Field on Conformational Energetics and Properties of Organic Liquids. J. Am. Chem. Soc 1996, 118, 11225–11236. [Google Scholar]
- (22).Jorgensen WL; Tirado-Rives J Potential Energy Functions for Atomic-level Simulations of Water and Organic and Biomolecular Systems. Prot. Natl. Acad. Sci. USA 2005, 102, 6665–6670. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (23).Halgren TA Merck Molecular Forcie Field. I. Basis, Form, Scope, Parametrization, and Performance of MMFF94. J. Comput. Chem 1996, 17, 490–519. [Google Scholar]
- (24).Halgren TA Merck Molecular Forcie Field. II. MMFF94 Van der Waals and Electrostatic Parameters for Intermolecular Interactions. J. Comput. Chem 1996, 17, 520–552. [Google Scholar]
- (25).Halgren TA Merck Molecular Forcie Field III. Molecular Geometries and Electrostatic Parameters for Intermolecular Interactions. J. Comput. Chem 1996, 17, 553–586. [Google Scholar]
- (26).Bleiziffer P; Schaller K; Riniker S Machine Learning of Partial Charges Derived from High-Quality Quantum-Mechanical Calculations. J. Chem. Inf. Model 2018, 58, 579–590. [DOI] [PubMed] [Google Scholar]
- (27).Rai BK; Bakken GA Fast and Accurate Generation of Ab Initio Quality Atomic Charges using Nonparametric Statistical Regression. J. Comput. Chem 2013, 34, 1661–1671. [DOI] [PubMed] [Google Scholar]
- (28).Ivanov MV; Talipov MR; Timerghazin QK Genetic Algorithm Optimization of Point Charges in Force Field Development: Challenges and Insights. J. Phys. Chem. A 2015, 119, 1422–1434. [DOI] [PubMed] [Google Scholar]
- (29).Keith TA In The Quantum Theory of Atoms in Molecules: From Solid State to DNA and Drug Design; Matta CF, Boyd RJ, Eds.; Wiley-VCH Verlag GmbH & Co; KGaA, 2007; pp 61–94. [Google Scholar]
- (30).Krawczuk-Pantula A; Pérez D; Stadnicka K; Macchi P Distributed Atomic Polarizabilities from Electron Density. 1. Motivations and Theory. Trans. Am. Crystallogr. Assoc 2011, 42, 1–25. [Google Scholar]
- (31).Krawczuk A; Pérez D; Macchi P PolaBer: A Program to Calculate and Visualize Distributed Atomic Polarizabilities Based on Electron Density Partitioning. J. Appl. Crystallogr 2014, 47, 1452–1458. [Google Scholar]
- (32).Heid E; Hunt P; Schröder C Evaluating Excited State Atomic Polarizabilities of Chromophores. Phys. Chem. Chem. Phys 2018, 20, 8554–8563. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (33).Heid E; Szabadi A; Schroder C Quantum Mechanical Determination of Atomic Polarizabilities of Ionic Liquids. Phys. Chem. Chem. Phys 2018, 20, 10992–10996. [DOI] [PubMed] [Google Scholar]
- (34).Heid E; Heindl M; Dienstl P; Schröder C Additive polarizabilities of Halides in Ionic Liquids and Organic Solvents. J. Chem. Phys 2018, 149, 044302. [DOI] [PubMed] [Google Scholar]
- (35).Sadlej AJ Medium-Size Polarized Basis Sets for High-Level-Correlated Calculations of Molecular Electric Properties. Theor. Chim. Acta 1991, 79, 123. [Google Scholar]
- (36).Bayly CI; Cieplak P; Cornell W; Kollman PA A Well-Behaved Electrostatic Potential Based Method using Charge Restraints for Deriving Atomic Charges: The RESP model. J. Phys. Chem 1993, 97, 10269–10280. [Google Scholar]
- (37).Alenaizan’s restricted electrostatic potential (RESP) plugin to Psi4. https://github.com/cdsgroup/resp (accessed September 10, 2018).
- (38).Parrish RM; Burns LA; Smith DGA; Simmonett AC; DePrince AE; Hohenstein EG; Bozkaya U; Sokolov AY; Di Remigio R; Richard RM; Gonthier JF; James AM; McAlexander HR; Kumar A; Saitow M; Wang X; Pritchard BP; Verma P; Schaefer HF; Patkowski K; King RA; Valeev EF; Evangelista FA; Turney JM; Crawford TD; Sherrill CD Psi4 1.1: An Open- Source Electronic Structure Program Emphasizing Automation, Advanced Libraries, and Interoperability. J. Chem. Theory Comput 2017, 13, 3185–3197. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (39).Carr RA; Congreve M; Murray CW; Rees DC Fragment-Based Lead Discovery: Leads by Design. Drug Discovery Today 2005, 10, 987–992. [DOI] [PubMed] [Google Scholar]
- (40).Taylor RD; MacCoss M; Lawson ADG Rings in Drugs: Miniperspective. J. Med. Chem 2014, 57, 5845–5859. [DOI] [PubMed] [Google Scholar]
- (41).Boulanger E; Huang L; Rupakheti C; MacKerell AD; Roux B Optimized Lennard-Jones Parameters for Druglike Small Molecules. J. Chem. Theory Comput 2018, 14, 3121–3131. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (42).Mobley DL; Guthrie JP FreeSolv: A Database of Experimental and Calculated Hydration Free Energies, with Input Files. J. Comput.-Aided Mol. Des 2014, 28, 711–720. [DOI] [PMC free article] [PubMed] [Google Scholar]
- (43).Stone AJ Distributed Multipole Analysis: Stability of Large Basis Sets. J. Chem. Theory Comput 2005, 1, 1128–1132. [DOI] [PubMed] [Google Scholar]
- (44).Misquitta AJ; Stone AJ Distributed Polarizabilities Obtained using a Constrained Density-Fitting Algorithm. J. Chem. Phys 2006, 124, 024111. [DOI] [PubMed] [Google Scholar]
- (45).Friedman JH Greedy Function Approximation: A Gradient Boosting Machine. Ann. Statist 2001, 29, 1189–1232. [Google Scholar]
- (46).Schmidhuber J Deep Learning in Neural Networks: An Overview. Neural Networks 2015, 61, 85–117. [DOI] [PubMed] [Google Scholar]
- (47).Rosenblatt F The Perceptron: A Probabilistic Model for Information Storage and Organization in The Brain. Psychological Review 1958, 65–386. [DOI] [PubMed]
- (48).Rumelhart DE; Hinton GE; Williams RJ Learning Representations by Back-Propagating Errors. Nature 1986, 323, 533–536. [Google Scholar]
- (49).Hutter F; Hoos H; Leyton-Brown K An Efficient Approach for Assessing Hyperparameter Importance. In ICML’14 Proceedings of the 31st International Conference on Machine Learning, Beijing, China, June 21–26, 2014; Xing EP, Jebara T, Eds.; PMLR, 2014; pp 754–762. [Google Scholar]
- (50).Wald A Statistical Decision Functions. Ann. Math. Statist 1949, 20, 165–205. [Google Scholar]
- (51).Glorot X; Bengio Y Understanding the Difficulty of Training Deep Feedforward Neural Networks. In Proceedings of the Thirteenth International Conference on Artificial Intelligence and Statistics, Sardinia, Italy, May 13–15, 2010; Teh YW, Titterington M, Eds.; PMLR, 2010; pp 249–256. [Google Scholar]
- (52).Burnham KP; Anderson DR Model Selection and Multimodel Inference: A Practical Information-Theoretic Approach, 2nd ed.; Springer-Verlag: New York, 2002. [Google Scholar]
- (53).Geisser S Predictive Inference; CRC Press: New York, 1993. [Google Scholar]
- (54).Kingma DP; Ba J Adam: A Method for Stochastic Optimization arXiv:1412.6980 arXiv.org cs, 2014; https://arxiv.org/abs/1412.6980 (accessed October 10, 2018).
- (55).Hahnloser RHR; Sarpeshkar R; Mahowald MA; Douglas RJ; Seung HS Digital Selection and Analogue Amplification Coexist in a Cortex-Inspired Silicon Circuit. Nature 2000, 405, 947–951. [DOI] [PubMed] [Google Scholar]
- (56).Clevert D-A; Unterthiner T; Hochreiter S Fast and Accurate Deep Network Learning by Exponential Linear Units (ELUs) arXiv:1511.07289 arXiv.org cs, 2015; https://arxiv.org/abs/1511.07289 (accessed October 10, 2018).
- (57).Department of Computational Biological Chemistry. http://www.mdy.univie.ac.at/python-stuff/predict_pol_charge_1.0.tar.gz (accessed December 1, 2018).
- (58).MacKerell Lab. http://mackerell.umaryland.edu/ (accessed December 1, 2018).
- (59).CGenFF. https://cgenff.umaryland.edu/ (accessed December 1, 2018).
- (60).Koch U; Stone AJ Conformational Dependence of the Molecular Charge Distribution and its Influence on Intermolecular Interactions. J. Chem. Soc., Faraday Trans 1996. , 92, 1701–1708. [Google Scholar]
- (61).Söderhjelm P; Kongsted J; Ryde U Conformational Dependence of Isotropic Polarizabilities. J. Chem. Theory Comput 2011, 7, 1404–1414. [DOI] [PubMed] [Google Scholar]


