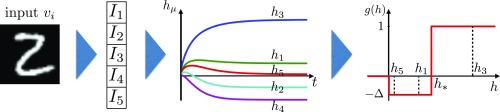
Fig. 2.

The pipeline of the training algorithm. Inputs $v_i$ are converted to a set of input currents $I_{\mu }$. These currents define the dynamics [8] that lead to the steady-state activations of the hidden units. These activations are used to update the synapses using the learning rule [3]. The learning activation function changes the sign at $h_{*}$, which separates the Hebbian and anti-Hebbian learning regimes. The second term in the plasticity rule [3], which is the product of the input current $I_{\mu }$ and the weight $W_{\mu i}$, corresponds to another path from the data to the synapse update. This path is not shown here and does not go through Eq. 8.