A Comparison of Three Fiber Tract Delineation Methods and Their Impact on White Matter Analysis

Abstract

Diffusion magnetic resonance imaging (dMRI) is an important method for studying white matter connectivity in the brain in vivo in both healthy and clinical populations. Improvements in dMRI tractography algorithms, which reconstruct macroscopic three-dimensional white matter fiber pathways, have allowed for methodological advances in the study of white matter; however, insufficient attention has been paid to comparing post-tractography methods that extract white matter fiber tracts of interest from whole-brain tractography. Here we conduct a comparison of three representative and conceptually distinct approaches to fiber tract delineation: 1) a manual multiple region of interest-based approach, 2) an atlas-based approach, and 3) a groupwise fiber clustering approach, by employing methods that exemplify these approaches to delineate the arcuate fasciculus, the middle longitudinal fasciculus, and the uncinate fasciculus in 10 healthy male subjects. We enable qualitative comparisons across methods, conduct quantitative evaluations of tract volume, tract length, mean fractional anisotropy, true positive and true negative rates, and report measures of intra-method and inter-method agreement. We discuss methodological similarities and differences between the three approaches and the major advantages and drawbacks of each, and review research and clinical contexts for which each method may be most apposite. Emphasis is given to the means by which different white matter fiber tract delineation approaches may systematically produce variable results, despite utilizing the same input tractography and reliance on similar anatomical knowledge.

1. Introduction

Diffusion magnetic resonance imaging (dMRI) is one of the most important methods for studying the connectivity and integrity of white matter pathways in the brain. Diffusion images are commonly analyzed using tractography, a method that reconstructs three-dimensional white matter fiber pathways in vivo based on water diffusion orientation information at each image voxel (Jones et al., 1999; Lazar et al., 2003; Malcolm et al., 2010; Mori et al., 1999). Tractography is widely used to investigate potential white matter pathology in psychiatric disorders (e.g., see review by Kubicki et al., 2007), cognitive disorders (e.g., Chua et al., 2008), nervous system disorders (e.g., Horsfield and Jones, 2002), mild traumatic brain injury (e.g., Shenton et al., 2012), and aging (e.g., Sullivan and Pfefferbaum, 2006), as well as in analyses that aim to uncover white matter trajectories and characterize the architecture of brain connectivity in healthy and diseased individuals (Catani et al., 2002; Essayed et al., 2017; Gong et al., 2009; Jolles et al., 2016; Makris et al., 2013a, 2013b, 2009, 2007, 2005, 2002; Rojkova et al., 2016; Sherbondy et al., 2005; Wakana et al., 2004).

Recent emphasis on improving dMRI tractography algorithms has allowed for significant methodological advances in the study of white matter fiber tracts, namely, the capacity to handle branching or crossing fibers, and the ability to reconstruct tracts in areas of low signal (Behrens et al., 2003; Malcolm et al., 2010; Parker et al., 2003; Tournier J-Donald et al., 2012). To date, a fair amount of work has been dedicated to comparing different tractography algorithms (Behrens et al., 2007; Bürgel et al., 2009; Fillard et al., 2011; Jones, 2008; Khalsa et al., 2014; Tensaouti et al., 2011) and to assessing or validating tractography against post-mortem tract tracing (Dauguet et al., 2007; Donahue et al., 2016; Dyrby et al., 2007; Knösche et al., 2015; Seehaus et al., 2013), diffusion phantoms (Fillard et al., 2011; Fritzsche et al., 2010; Poupon et al., 2008; Pullens et al., 2010), and simulated ground truth bundles (Maier-Hein et al., 2017). After tractography algorithms generate potential macroscopic fiber pathways, or “streamlines”, however, anatomical and functional interpretation of the tractography results remains ambiguous until streamlines are grouped into distinctive white matter bundles based either on the morphology of known white matter tracts, or on an understanding of the brain structures the streamlines connect. Nevertheless, insufficient attention has been paid to directly comparing tractography post-processing methods that facilitate white matter bundle delineation and extraction, despite the fact that different methodologies may produce inconsistent or discrepant output. A more comprehensive understanding of potential methodological differences is needed in order to enable (or prevent) appropriate (or inappropriate) comparisons of results across studies, and in order to better appreciate the relative advantages and limitations of diverse methods.

Tractography streamlines can be generated from whole brain diffusion data, i.e. “whole-brain tractography”, by simultaneously placing seed points throughout all voxels in the brain. Subsequently, white matter tracts of interest can be identified and extracted from the whole-brain tractography. Three methods are commonly employed to accomplish this: 1) manually placing regions of interest (ROIs) around the “stems” (the most compact portions) of fiber bundles (Catani et al., 2002; Catani and Thiebaut de Schotten, 2008a; Conturo et al., 1999; Mori et al., 2002; Sherbondy et al., 2005; Wakana et al., 2007); 2) selecting tractography streamlines based on the atlas-defined gray matter or white matter regions they penetrate or terminate in (Hua et al., 2008; Lawes et al., 2008; Suarez et al., 2012; Wassermann et al., 2016; Yendiki et al., 2011; Zhang et al., 2010); and 3) grouping streamlines into clusters based on fiber similarity properties (Brun et al., 2004; Ding et al., 2003; Garyfallidis et al., 2012; Guevara et al., 2012; O’Donnell and Westin, 2007).

Manual ROI methods (see 1 above) involve identifying and drawing inclusionary and exclusionary ROIs on Fractional Anisotropy (FA) or color-by-orientation Diffusion Tensor Image (DTI) maps, and selecting only the streamlines that pass through inclusionary ROIs. White matter fiber pathways are typically organized into three portions, a compact, homogenous bundle, called the “stem”, an area of fiber divergence, the “spray”, and a widespread peripheral area with fiber terminations, referred to as the “extreme periphery” (Makris et al., 1997). Manual methods traditionally involve the placement of ROIs around tract stems, with ROI placement being guided by methodologies established in the literature, or by a neuroanatomist who is an expert in white matter anatomy. Manual ROI methods are considered the gold standard for white matter delineation given their subject-specific nature, their reliance on expert neuroanatomical knowledge, and their potential for high inter-rater and intra-rater reliability with regards to ROI placement, ROI volume, tract streamline number, and tract measures such as FA (Catani and Thiebaut de Schotten, 2008a; Malykhin et al., 2008; Wakana et al., 2007). Nonetheless, proper placement of ROIs, essential for accuracy, reliability and reproducibility, necessitates that the experimenter has neuroanatomical knowledge and is precise with ROI placements, and that the ROI methodology being utilized is robust. Manual methods additionally have inherent shortcomings in that they are very time-intensive, and they can only be utilized to delineate previously identified white matter pathways with known, uncomplicated trajectories (Zhang et al., 2010).

To address issues of time, labor, and ease of reproducibility, automated approaches to white matter tract delineation have been developed. Atlas-based methods (see 2 above) are automated approaches that require anatomical atlases and diffusion images or DTIs to be co-registered prior to tract extraction. White matter tract extraction then follows a set of instructions, which dictates which atlas-defined gray and/or white matter ROIs each fiber tract should (and should not) pass through. Atlas-based methods allow for the extraction of a large number of white matter tracts in an efficient and reproducible manner, using protocols that are transparent to users and that minimize experimenter bias and the need for anatomical knowledge. Furthermore, in addition to being utilized to study well known white matter tracts, these methods are perhaps best suited for exploratory analyses. However, high quality output using these methods is contingent upon accurate registration of the atlas in use to each subject’s data, and tract definitions are constrained to ROIs that are included in the atlas (e.g., atlases from Desikan et al., 2006; Fischl et al., 2002; Mori et al., 2011; Oishi et al., 2009; Varentsova et al., 2014).

Fiber clustering approaches (see 3 above) are alternate automated methods for white matter analysis, wherein whole-brain tractography is grouped into a number of “fiber clusters” in a data-driven manner. Specifically, fiber clustering methods group streamlines that follow similar anatomical pathways into distinctive clusters, and groupwise clustering methods additionally identify and extract homologous clusters from all subjects (O’Donnell and Westin, 2007). This data-driven method could be considered initially anatomically unbiased, as no a priori anatomical information is input into the clustering algorithm. Subsequent to clustering, however, individual clusters can be visualized and identified as part of larger white matter tracts, though this often requires advanced neuroanatomical knowledge. Groupwise clustering methods may prove most beneficial for reliably identifying anatomically similar portions of white matter across subjects (O’Donnell et al., 2013); however, they may also reduce the ability to examine between-subject variability in tract shape and architecture. Furthermore, groupwise methods require co-registration of subjects’ whole brain tractography to the same three-dimensional space, which introduces the potential for registration errors that can affect cluster classification.

Validation of automated white matter delineation methods typically entails demonstrating that a given method produces similar results to those obtained from a manual ROI method, as these are presumed to be the most specific and anatomically accurate methods available. Typically, a kappa value (k) is calculated to measure inter-method agreement between an automated and a manual ROI method, with a k > .60 indicating “substantial” agreement between methods, and a k > .80 indicating “almost perfect” agreement (Landis and Koch, 1977). Previous comparisons of manual and atlas-based white matter delineation methods have generally reported substantial agreement, with kappa values averaging around .75, and ranging from .65 to .95 (Wassermann et al., 2016; Zhang et al., 2010, 2008). Similar kappa values have also been found for comparisons of fiber clustering results to manual methods (Voineskos et al., 2009). It is not entirely evident, however, how fiber clustering and atlas-based methods may compare (although see Guevara et al., 2012; Yoo et al., 2015), or what analyses that extend beyond kappa values will reveal. The ways in which manual ROI-based, atlas-based, and groupwise fiber clustering methods differentially impact results obtained from the same dataset has yet to be extensively investigated.

The goal of the present study is to conduct a head to head comparison of three distinct post-processing methods used for white matter tract extraction that exemplify three major conceptual approaches to tract delineation. These methods are separately applied to the same data, thus ensuring that preprocessing and tractography generation steps are equivalent across methods. This is the first study, to the best of our knowledge, to comprehensively compare examples from a manual ROI-based, a cortical atlas-based, and a data-driven approach. We utilize three methods that represent these approaches—Manual Multiple-ROI Labeling (guided by Catani and Thiebaut de Schotten (2008a)), The White Matter Query Language (Wassermann et al., 2016), and Data-Driven Groupwise Fiber Clustering (O’Donnell and Westin, 2007)—to extract three widely studied, functionally significant, and anatomically distinctive white matter tracts, namely: the arcuate fasciculus (a large, arcing fiber bundle), the middle longitudinal fasciculus (a long, straight, horizontal fiber bundle), and the uncinate fasciculus (a hook-shaped fiber bundle with a compact stem). We examine each method’s influence on tract shape, tract volume, tract length, fractional anisotropy and anatomical connectivity, enable visualization of areas within each tract where the three methods are predominantly convergent and divergent, and compute Jaccard Coefficients and Intraclass Correlation Coefficients, standard methods employed to evaluate inter-method spatial overlap and inter-method reliability, respectively. We additionally report intra-method sensitivity, a measure of the extent to which each method correctly identifies fibers that do belong to a given tract (i.e. true positives), and intra-method specificity, a measure of how often each method correctly identifies white matter regions that are not part of a given tract (i.e. true negatives). Methodological similarities and differences across the three approaches are discussed, and the clinical and research contexts for which each approach may be most apposite are reviewed.

2. Methods

2.1. Image Acquisition and Preprocessing

Magnetic Resonance (MR) Images from 10 healthy, right-handed male subjects (mean age: 22.29 years, standard deviation: 1.68) were included in the analysis. Images were acquired as part of the larger Boston Center for Intervention Development and Applied Research (CIDAR) study (www.bostoncidar.org). Inclusion and exclusion criteria are described in Lee et al. (2013). Images were obtained on a 3-Tesla whole body MRI Echo speed system General Electric scanner (GE Medical Systems, Milwaukee) at the Brigham and Women’s Hospital, Boston, MA. Diffusion images were acquired using an echo planar image sequence with the following parameters: TR/TE=17000 ms/78 ms; 51 gradient directions with b=900 s/mm² and 8 additional b=0 images. Each volume consisted of 85 axial slices of 1.7 mm thickness, and had an acquisition matrix of 144×144 in a field of view of 240×240 mm², and a voxel dimension of 1.7×1.67×1.67 mm. T1-weighted and T2-weighted images were acquired with the following parameters: 176 slices, TR/TE= 7.4 ms/3 ms, TI = 600, 10° flip angle, acquisition matrix of 256 × 256, field of view of 256×256 mm², and a voxel dimension of 1×1×1 mm.

Images were visually examined to ensure high quality prior to preprocessing. Preprocessing steps for the diffusion data included motion and eddy current correction using an affine registration algorithm in FSL (http://www.fmrib.ox.ac.uk/fsl), followed by EPI geometric distortion correction using an in-house script and advanced normalization tools’ (ANTS) symmetric diffeomorphic mapping (Avants et al., 2008) to warp the diffusion image along the phase encoding direction to an undistorted T2-weighted image (https://github.com/pnlbwh/pnlutil). Diffusion tensor images were estimated from the diffusion data in 3D Slicer Version 4.5 (https://www.slicer.org) via the SlicerDMRI project (http://dmri.slicer.org) (Norton et al., 2017) using a weighted-least-squares estimation. Whole-brain two-tensor tractography was computed using a multi-fiber tracking algorithm that utilizes an Unscented Kalman Filter (UKF) (described in (Malcolm et al., 2010)), with a free water correction applied (Baumgartner et al., 2012). This multi-tensor UKF tractography algorithm recursively estimates tensor model parameters (e.g. eigenvalues and eigenvectors) and local fiber orientation along each point in a streamline based on the previous point, allowing the algorithm to perform well in the presence of noise and uncertainty (Fillard et al., 2011; Malcolm et al., 2010, 2009) as well as in the presence of crossing fibers (Baumgartner et al., 2012; Fillard et al., 2011).

T1-weighted images were processed with FreeSurfer (Fischl, 2012), a publicly available software package (http://www.martinos.org/freesurfer), in order to parcellate brain gray and white matter into distinct anatomical regions. FreeSurfer’s gray and white matter parcellation is based on Fischl et al.’s (2004, 2002) automated neuroanatomical structure segmentation. FreeSurfer anatomical labelmaps were registered to diffusion space using ANTS by performing a rigid registration of the T1 to the T2, followed by a non-linear registration of the T2 to a diffusion b=0 volume, and applying a composite transformation to the FreeSurfer labelmap.

2.2. White Matter Tract Delineation Methods

Three tractography post-processing white matter tract (fiber tract) delineation methods were applied to data from the 10 subjects. The arcuate fasciculus (AF), the middle longitudinal fasciculus (MdLF) and the uncinate fasciculus (UF) were extracted from the whole-brain two-tensor tractography using the following methods: 1) Manual Multiple-ROI Labeling (Manual), in which ROIs are drawn around the stems of fiber bundles, 2) the White Matter Query Language (WMQL), a fully automated method that defines white matter tracts based on their endpoints in anatomically parcellated gray and white matter, and 3) Data-Driven Groupwise Fiber Clustering (Clustering), a semi-automated method that groups streamlines from whole-brain tractography into groups of fibers (“fiber clusters”) based on fiber similarity properties.

2.2.1. Manual Multiple-ROI Labeling (Manual)

White matter ROIs were identified and drawn manually on color-by-orientation (directionally encoded color) DTI maps using 3D Slicer. Inclusion and exclusion ROIs were drawn for the AF, the MdLF, and the UF. ROI placement was based on current anatomical knowledge of tract trajectories. Color-by-orientation DTI maps follow an RGB (red-green-blue) scheme (Makris et al., 1997) to indicate the major eigenvector direction, which aligns with the direction of major white matter tracts (Beaulieu, 2002) (red: left-right, green: anterior-posterior, blue: dorsal-ventral). Anatomical ROI definitions for the AF and the UF were derived from the procedures specified by Catani and Thiebaut de Schotten (2008a). ROI definitions for the MdLF were based on criteria described in Makris et al. (2013), as this tract is not included in Catani and Thiebaut de Schotten (2008a). Streamlines identified using the whole-brain two-tensor tracking algorithm that penetrated the manually defined inclusion ROIs (and did not penetrate exclusion ROIs) were assigned to the white matter tract associated with those ROIs.

The AF is an arcing fiber bundle that connects the inferior frontal gyrus to the middle temporal gyrus, the posterior portion of the superior temporal gyrus, and portions of the lateral temporo-occipital transition regions (Catani et al., 2005; Makris et al., 2005). The stem of the AF was delineated with 2 inclusion ROIs drawn in the axial plane, and 2 exclusion ROIs drawn in coronal and sagittal planes (Figure 1A).

Figure 1.

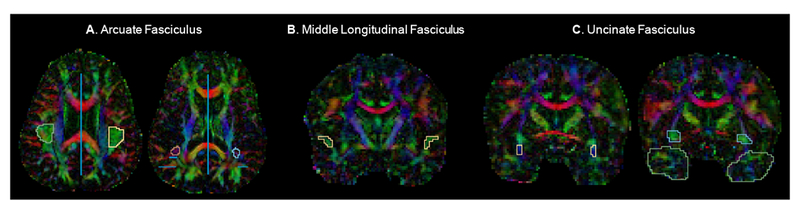
Example regions of interest (ROIs) drawn for manual delineation of the A. arcuate fasciculus (AF), B. middle longitudinal fasciculus (MdLF), and C. uncinate fasciculus (UF) displayed on diffusion tensor color maps. The 2 circular inclusion ROIs can be seen for the right and left AF. Blue lines represent AF exclusion ROIs. One of four inclusion ROIs can be seen for both the right and left MdLF. All 3 inclusion ROIs can be seen for both the right and left UF. Exclusion ROIs are not visible in these slices for the MdLF and the UF.

The MdLF is a long, horizontally-oriented fiber bundle beginning in the temporal pole that runs within the superior temporal gyrus and bifUrcates caudally to connect to the angular gyrus (Makris and Pandya, 2009) and the superior parietal lobule (Makris et al., 2013; Wang et al., 2013). The stem of the MdLF was identified with 4 inclusion ROIs and 2 exclusion ROIs drawn in the coronal plane (Figure 1B).

The UF is a hook-shaped fiber bundle that connects the anterior temporal lobe and the frontal lobe, where it spans medial and lateral regions, extending into orbital regions and the middle and inferior frontal gyri (Makris et al., 1997). The stem of the UF was delineated using 3 inclusion ROIs and 2 exclusion ROIs drawn in the coronal plane (Figure 1C).

Intra-rater reliability was calculated for the extraction of white matter tracts using the Manual Multiple-ROI Labeling method via a two-way random Intraclass Correlation analysis with measures of absolute agreement. Intra-rater reliability was excellent for tract volume (AF: ICC= 0.92, MdLF: ICC= 0.81, UF: ICC= 0.94) and FA (AF: ICC= 0.99, MdLF: ICC= 0.90, UF: ICC= 0.99).

2.2.2. White Matter Query Language (WMQL)

WMQL (Wassermann et al., 2016) is an automated fiber tract delineation method in which white matter tracts are defined, from a theoretical standpoint, by the regions of brain gray matter they are understood to connect. White matter tracts are delineated in WMQL by identifying streamlines that connect specified ROIs in the FreeSurfer atlas, namely, FreeSurfer ROIs that are included in a given tract’s anatomical “definition”. Tract definitions in WMQL are written as queries (created by expert anatomist NM), which inform the software which streamlines to extract from whole-brain tractography. Table 1 contains the WMQL query definitions used to extract the AF, the MdLF and the UF. The queries are an updated version of those originally presented in Wassermann et al. (2016); updates reflect improvements following query testing and modification by NM and colleagues. It should be noted that the anatomical regions specified in the queries in Table 1 include both the corresponding cortical region and the adjacent white matter region. For example, “temporalpole.side” includes both the FreeSurfer region “ctx-*h-temporalpole” and the region “wm-*h-temporalpole”.

Table 1. White Matter Query Language Tract Definitions.

White Matter Tract	WMQL Query Definition
Arcuate Fasciculus	AF.side = ((inferior_frontal_gyrus.side or middle_frontal_gyrus.side or precentral.side) and (superiortemporal.side or middletemporal.side) not in hemisphere.opposite, not in medial_of(supramarginal.side), not in ilf.side, not in ioff.side, not in ex.side, not in mdlf.side, not in mdlf_probable_sections.side, not in temporalpole.side, not in frontalpole.side, not in subcortical.side, not in rostralmiddlefrontal.side, not in lateralorbitofrontal.side, not in parstriangularis.side, not in superfrontal.side, not in parsopercularis.side)
Middle Longitudinal Fasciculus	MdLF.side = only((temporalpole.side or superiortemporal.side) and (inferiorparietal.side or superiorparietal.side or supramarginal.side or precuneus.side or (UnsegmentedWhiteMatter.side and superiorparietal.side) or (UnsegmentedWhiteMatter.side and inferiorparietal.side)))
Uncinate Fasciculus	UF.side = ((orbitofrontalgyrus.side or inferior_frontal_gyrus.side) and endpoints_in(temporalpole.side) and insula.side) not in occipital.side, not in parietal.side, not in cingular.side, not in posterior_of(putamen.side), not in hemisphere.opposite)

2.2.3. Data-Driven Groupwise Fiber Clustering (Clustering)

Spectral fiber clustering was implemented using the freely available pipeline first described in O’Donnell and Westin (2007) (https://github.com/SlicerDMRI/whitematteranalysis). First, a groupwise entropy-based registration was performed in order to register whole-brain tractography from each of the 10 subjects into a common space (referred to as group space) (O’Donnell et al., 2012). A high-dimensional, study-specific, multi-subject clustering atlas was then generated by grouping subsets of fibers from all 10 subjects into 800 distinct clusters. Clusters were created based on fiber distance, fiber shape, and cluster commonality across hemispheres and across subjects, following the method described in O’Donnell and Westin (2007). Four iterations of group outlier detection were performed during the generation of the multi-subject clustering atlas, by iteratively clustering and identifying outlier fibers that had a low probability (more than 2 standard deviations away from cluster mean probability) of belonging to a given cluster. The multi-subject clustering atlas was then used to group tractography from each individual subject into 800 homologous white matter clusters; only streamlines with a fiber length of greater than 50 mm were clustered. Finally, subject-specific outlier removal was performed to remove potentially aberrant fibers from subject clusters, again with a threshold of 2 standard deviations.

All 800 clusters were visually examined for each of the 10 subjects in order to determine candidate clusters for the AF, the MdLF, and the UF. Clusters with fibers that were primarily part of a given tract in at least 70% of subjects were included in the finalized tract. Decisions were guided by an anatomical expert (NM). The AF was best characterized by a subset of 15 clusters in all subjects, the MdLF by 9 clusters, and the UF by 8 clusters. Tracts were extracted and registered from group space back to subject space using an inverse transform.

2.3. Qualitative Comparisons of Intra- and Inter-Method Overlap: Method-Specific Tract Overlay Maps and Tract Heatmap Generation

2.3.1. Method-Specific Tract Overlay Maps for Intra-Method Overlap

To allow for a qualitative comparison of the three methods, method-specific tract overlay maps were generated, for each method, to visually represent the extent of tract overlap across subjects. To generate the method-specific tract overlay maps, the 90 subject-specific fiber tracts were converted into binary subject-specific tract masks by assigning a label value of 1 to all voxels that contained tract streamlines. The resultant subject-specific tract masks were registered to the MNI152 T1-weighted standard brain, to allow for overlap quantification. A series of registration steps was carried out with ANTS, as follows: a nonlinear transformation from subject diffusion space to subject T2 space, a rigid transformation from subject T2 space to subject T1 space, a nonlinear transformation from subject T1 space to the MNI152 T1 template. Following registration, binary method-specific tract overlay maps with an inclusion threshold of 50% of subjects were created. Specifically, for each method/tract, voxels that were labeled as “1” in at least 50% of subjects were assigned a value of 1, and voxels that were labeled as “1” in less than 50% of subjects were assigned a value of 0. The resulting method-specific tract overlay maps thereby display the degree of intra-method tract overlap. The 50% inclusion threshold was chosen in order to identify voxels that had streamlines in a majority of subjects (and thus represented a consistent anatomical tract feature), while still conserving a level of between-method variability in overlap. Volume rendering was performed on the binary method-specific tract overlay maps to generate 3D models for visualization.

2.3.2. Heatmaps for Inter-Method Overlap

The binary method-specific tract overlay maps generated for each method for the AF, the MdLF and the UF were overlaid on the MNI152 template to produce heatmaps that display spatial agreement across the three methods. Heatmaps were used to enable visualization of tracts areas where the three methods have high and low degrees of overlap.

2.4. Quantitative Comparisons

The following measures were used to quantitatively evaluate similarities and differences across the three methods: a) Volumes of the Method-Specific Tract Overlay Maps (see 2.3.1); b) Intraclass Correlation Coefficients; c) Normalized Tract Volume; d) Tract Length; e) FA; f) The Jaccard Coefficient; g) Simultaneous Truth and Performance Level Estimation (STAPLE) Algorithm sensitivity and specificity (Warfield et al., 2004).

2.4.1. The Jaccard Coefficient (JC)

The JC is a similarity measure that evaluates the degree of agreement between two datasets. It is defined as the size of the intersection over the size of the union, JC = |X ∩ Y|/|X ∪ Y|, where X and Y are two sets of voxels obtained from binary subject-specific tract masks produced by methods “X” and “Y”. A JC was computed for each method pair (i.e., Manual and WMQL, Manual and Clustering, and Clustering and WMQL) by computing the JC for each method pair for each subject, and taking the average across subjects. Additionally, a JC was computed to measure agreement among the three methods, JC = (|X ∩ Y ∩ Z|/|X ∪ Y ∪ Z|), by computing subject-specific JCs and taking the average across all ten subjects. In the three method JC, the numerator represents the number of voxels labeled as 1 in subject-specific tract masks in all three methods, and the denominator represents the total number of voxels labeled as 1 in any of the three methods.

2.4.2. The Simultaneous Truth and Performance Level Estimation Algorithm

The STAPLE algorithm (Warfield et al., 2004) utilizes information from segmentations produced by multiple methods in order to estimate an optimal combination of the segmentations based on common agreement across inputs. Each input segmentation is assigned a weight depending on its estimated performance level. The probabilistic optimal segmentation and method-specific performance levels are estimated iteratively via an Expectation-Maximization (EM) algorithm. Performance level measures for each method with respect to estimated common agreement are expressed in terms of sensitivity (“p”) and specificity (“q”), which, here, were calculated for each tract generated by each method. The sensitivity measure (p) referenced throughout this paper represents the “true positive rate”, and is equal to the percentage of voxels that are correctly identified as being part of a tract, and the specificity measure (q) described here represents the “true negative rate” and reflects the percentage of voxels that are correctly identified as not being part of a tract. These measures will be affected by both between and within method variability; methods that are internally consistent and that have greater spatial overlap with the other methods under consideration will generally have better performance (higher p and q) than methods that are internally variable or that have lower spatial agreement with other methods.

2.5. Streamline Endpoint Analysis

To compare tract anatomical connectivity across methods, a streamline endpoint analysis was conducted using FreeSurfer anatomical labelmaps registered to diffusion images. For each region in the FreeSurfer atlas, the percentage of a given tract’s streamlines with endpoints in that region was computed. Percentages for each region were averaged over all subjects for each method and tract, and regions containing at least 5% of AF, MdLF or UF streamline endpoints were identified.

2.6. Statistical Analyses

Statistical analyses were conducted with SPSS Version 23. Mean and standard deviations for tract volume, tract length, and FA were obtained. Separate ANOVAs were conducted to compare mean tract volume, mean tract length, and mean FA values for the AF, the MdLF and the UF (1 ANOVA for each measure and each tract). Tract volume and FA were entered as the dependent variables, and ‘hemisphere’ and ‘method’ as the independent variables. If a significant main effect of ‘method’ was found, post-hoc Bonferroni-corrected t-tests were conducted.

3. Results

3.1. Qualitative Comparisons

3.1.2. Method-Specific Tract Overlay Maps: Intra-Method Overlap

Method-specific tract overlay maps were generated for the right and left AF, MdLF, and UF, to evaluate the degree of tract overlap within each of the three methods. Figure 3 displays the 3D volume renderings of these maps. Groupwise Fiber Clustering (Clustering) maps are displayed in green, Manual Multiple-ROI Labeling (Manual) maps in blue, and White Matter Query Language (WMQL) maps in red. The 3D volume models reveal tracts of similar shape and size across methods, however several differences should be noted. Across the AF models, each method generates a distinct anatomical feature not seen in the other two methods. For Clustering, it takes the form of a posterior projection off of the dorsal portion of the tract’s arch. For the Manual method, the AF extends further anteriorly towards the frontal pole. For WMQL, the AF includes fibers connecting the dorsal and ventral portions of the tract. Across the MDLF models, Clustering generates a tract with a larger stem and spray, and across the UF models, WMQL generates a tract with a smaller stem and spray.

Figure 3.

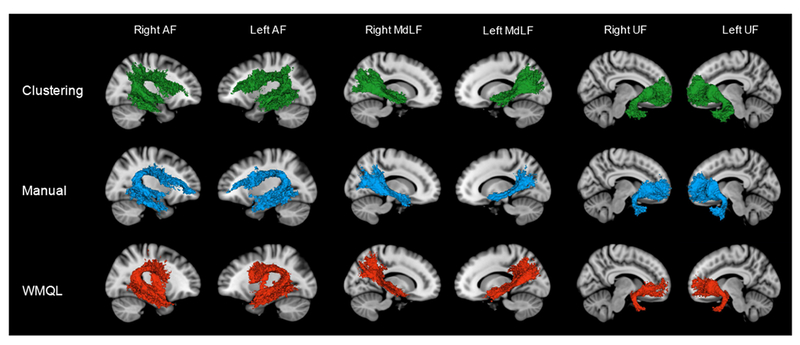
3D Models of the method-specific tract overlay maps generated by Data-Driven Groupwise Fiber Clustering (green), Manual Multiple-ROI Labeling (blue) and the White Matter Query Language (red). Method-specific tract overlay maps were obtained by overlaying binarized tract masks from all 10 subjects in MNI152 space and labeling voxels that were present in at least 50% of subjects, thus capturing the degree of intra-method tract overlap.

3.1.3. Heatmaps: Inter-Method Overlap

To evaluate the degree to which the three methods overlap spatially when delineating the AF, the MdLF and the UF, heatmaps were created for each tract (Figure 4).

Figure 4.

Representative axial, coronal, and sagittal views of tract stem and tract spray regions of the AF, the MdLF, and the UF are shown. Binarized method-specific tract overlay maps generated for each method and tract were overlaid on the MNI152 T1 template to produce heatmaps that display spatial agreement across the three methods. Red areas depict voxels where streamlines were present from all three methods. Orange areas depict voxels where streamlines were present from two out of three methods. Yellow areas depict voxels where streamlines were present from one method only.

3.2. Quantitative Comparisons

3.2.1. Method-Specific Tract Overlay Map Volumes

Volumes of the method-specific tract overlay maps (displayed in Figure 3) are provided in Table 2. Volumes are largest for the tracts produced by Clustering. Manual volumes are larger than WMQL volumes for the AF and the UF, but smaller for the MdLF.

Table 2. Volumes of the Method-Specific Tract Overlap Maps.

Tract overlay maps (displayed in Figure 3) were obtained by overlaying binarized tract masks from all 10 subjects in MNI152 space and labeling voxels that were present in at least 50% of subjects. This table displays the volume of the region with greater than 50% intra-method overlap.

White Matter Tract	Method	Volume (mm^3)
	Clustering	40,850
Arcuate Fasciculus	Manual	29,996
	WMQL	24,179
Middle Longitudinal Fasciculus	Clustering	19,770
	Manual	10,341
	WMQL	17,715
	Clustering	27,600
Uncinate Fasciculus	Manual	21,231
	WMQL	9,455

3.2.2. Intraclass Correlation Analysis

Inter-method reliability was evaluated with an ICC analysis. Two-way mixed ICCs with measures of absolute agreement were calculated for each fiber tract, based on tract volume. The degree of consistency among the three methods was highest for the UF (ICC=0.727, Cronbach’s alpha=0.863), followed by the AF (ICC=0.616, Cronbach’s alpha=0.743) and the MdLF (ICC=0.348, Cronbach’s alpha=0.505), representing excellent (UF and AF) and fair (MdLF) agreement.

3.2.3. Tract Volume, Tract Length, and Fractional Anisotropy

Tract Volume, Tract Length, and FA values (Table 3) were compared between methods. Volume and length measurements were largely variable across methods, with no apparent pattern across methods or tracts. FA values were consistent across methods for the AF; differences were within .01. FA values were slightly more variable for the MdLF and the UF, with Clustering exhibiting the highest FA, followed by Manual, and then WMQL.

Table 3. Tract-Derived Measures.

Mean (S.D.) normalized tract volume (absolute tract volume divided by total intracranial volume), tract length, and fractional anisotropy measures obtained from individual subject white matter tracts.

White Matter Tract	Method	Normalized Tract Volume	Tract Length	FA
Arcuate Fasciculus	Clustering	.069 (.008)	95.6 (6.0)	0.615 (0.02)
	Manual	.063 (.012)	98.5 (10.8)	0.625 (0.02)
	WMQL	.056 (.011)	100.5 (6.3)	0.616 (0.02)
Middle Longitudinal Fasciculus	Clustering	.040 (.004)	93.6 (5.2)	0.624 (0.02)
	Manual	.050 (.007)	83.1 (9.4)	0.596 (0.03)
	WMQL	.043 (.007)	65.9 (10.1)	0.590 (0.03)
Uncinate Fasciculus	Clustering	.041 (.005)	100.8 (4.7)	0.614 (0.03)
	Manual	.039 (.007)	87.3 (9.7)	0.585 (0.03)
	WMQL	.033 (.008)	84.1 (9.2)	0.566 (0.03)

ANOVAs were conducted for each fiber tract (AF, MdLF, UF) and measure (tract volume, tract length, and FA). The analysis of tract volume showed a significant main effect of method for all three fiber tracts (AF: F_(2,57)=8.646, p=.001; MdLF: F_(2,57)=14.304, p<0.001; UF: F_(2,57)=7.776, p=.001). Post-hoc analyses revealed differences between Clustering and WMQL for the AF (p < .0001), between Clustering and Manual (p < .0001) and WMQL and Manual (p= .001) for the MDLF, and between Clustering and WMQL (p= .001) and WMQL and Manual (p=.013) for the UF (see Figure 5A). The analysis of tract length showed a significant main effect of method for the MdLF (F_(2,57)=53.815, p<0.001) and the UF (F(₂,₅₇)=23.527, p<0.001). Tract length was longer for Clustering than for Manual (p<0.001) and WMQL (p<0.001) in both tracts (Figure 5B). Likewise, the analysis of FA revealed a significant main effect of method for the MdLF (F(_2,57)=10.218, p<0.001) and the UF (F(_2,57)=15.282, p<0.001) only, and not for the AF (F(_2,57)=1.091, p=0.343). For both the MdLF and the UF, Clustering exhibited significantly greater FA than Manual (MDLF: p=002, UF: p=004) and WMQL (p<0.001 for MDLF and UF) (Figure 5C).

Figure 5.

Mean tract volume, tract length, and fractional anisotropy measures across methods.

* indicates significance

3.2.4. Jaccard Coefficients (JC)

Table 4 illustrates the degree of spatial overlap between methods, based on the JC. Overlap across all three methods was highest for the UF (JC=0.307), followed by the AF (JC=0.286) and the MdLF (JC=0.163) (Table 4). For the two-method comparisons, JCs were highest for Clustering and Manual, followed by Clustering and WMQL, and lowest for WMQL and Manual.

Table 4. Jaccard Coefficients.

Mean (S.D.) across- and between-method Jaccard Coefficients. JC= Jaccard Coefficient

White Matter Tract	3 Method JC	Clustering + Manual JC	Clustering + WMQL JC	Manual + WMQL JC
Arcuate Fasciculus	0.286 (0.070)	0.514 (0.078)	0.418 (0.075)	0.401 (0.082)
Middle Longitudinal Fasciculus	0.163 (0.036)	0.321 (0.061)	0.366 (0.066)	0.294 (0.047)
Uncinate Fasciculus	0.307 (0.067)	0.632 (0.076)	0.355 (0.068)	0.429 (0.079)
		Mean = 0.489	Mean = 0.379	Mean = 0.374

3.2.5. Sensitivity and Specificity Measures

Table 5 displays STAPLE sensitivity and specificity values for the three tract delineation methods. Sensitivity was highest for the Clustering method (mean=.860), followed by the Manual method (mean=.766) and WMQL (mean=.612). Sensitivity values (p) measure how often each method correctly identifies fibers that should belong to a given tract (true positives). Specificity (q) was high for all three tracts and methods (q > 0.99). Specificity values measure how often each method correctly identifies brain regions that should not be considered part of a given tract (true negatives).

Table 5. STAPLE Performance Level Measures.

Sensitivity and specificity values for each method computed by the STAPLE algorithm.

Method	Sensitivity (p)	Specificity (q)
Clustering	.860 (.102)	.998 (.0007)
Manual	.766 (.166)	.999 (.0005)
WMQL	.612 (.126)	.999 (.0008)

3.3. Streamline Endpoint Analysis

To compare anatomical connectivity across methods, a streamline endpoint analysis was conducted. Table 6 presents anatomical regions containing at least 5% of a given tract’s streamline endpoints by tract and method.

Table 6. Tract-Specific Anatomical Connectivity Across Methods.

An analysis of streamline endpoints based on FreeSurfer atlas regions. Regions displayed contained endpoints from at least 5% of a given white matter tract’s streamlines.

White Matter Tract	Method	Cortical FreeSurfer Regions with >= 5% of Streamline Endpoints	White Matter FreeSurfer Regions with >= 5% of Streamline Endpoints
Arcuate Fasciculus	Clustering	precentral gyrus +++ middle temporal gyrus +++ inferior temporal gyrus++ supramarginal gyrus	middle temporal wm +++ supramarginal wm
	Manual	precentral gyrus+++ middle temporal gyrus+++ inferior temporal gyrus++	middle temporal wm +++ inferior temporal wm
	WMQL	precentral gyrus+++ superior temporal gyrus middle temporal gyrus +++	precentral wm middle temporal wm +++
Middle Longitudinal Fasciculus	Clustering	superior temporal gyrus +++ superior parietal lobule ++ inferior parietal lobule +++	superior temporal wm +++ inferior parietal wm
	Manual	superior temporal gyrus +++ inferior parietal +++	superior temporal wm +++
	WMQL	superior temporal gyrus +++ superior parietal lobule ++ inferior parietal lobule +++supramarginal gyrus	superior temporal wm +++ superior parietal wm supramarginal wm
Uncinate Fasciculus	Clustering	superior frontal gyrus rostral middle frontal gyrus middle temporal gyrus ++ inferior temporal gyrus temporal pole gyrus +++
	Manual	middle temporal gyrus++ temporal pole gyrus +++	lateral orbitofrontal wm ++
	WMQL	temporal pole gyrus +++	lateral orbitofrontal wm ++ temporal pole wm

⁺⁺⁺Region appears in all three methods

⁺⁺Region appears in two methods

4. Discussion

This head to head comparison of three conceptually distinct approaches to white matter tract delineation—a manual multiple ROI-based approach, an atlas-based and a groupwise fiber clustering approach—corroborates that different approaches can extract similar white matter tracts from whole brain tractography. Differences between approaches in tract volume and length, FA, and intra-method tract overlap were, however, observed, as were incongruities in tract architecture and anatomical connectivity. Though some inter-method differences arise in an unsystematic manner, most observed dissimilarities occur systematically and can be explained by underlying differences in delineation strategy and methodology. Additionally, spatial agreement and metric consistency across approaches appear to be, to an extent, contingent upon the architecture of the tract of interest.

The qualitative output (Figures 2 and 3) substantiates that white matter tracts generated by the three methods are comparable in overall architecture, however differences in size, exemplified best by the MdLF and the UF, and alterations in tract anatomy, as seen with the AF, do occur. Heatmaps (Figure 4) depicting the degree of spatial overlap across methods for each tract illustrate that inter-method agreement is high in the stem of white matter tracts, though agreement decreases, and topological variability increases, at the spray and extreme periphery of tracts. Spatial agreement as measured by the Jaccard Coefficient was greatest between Manual and Clustering methods, most likely because the Manual method identifies fibers passing through the stems of white matter tracts, which tend to have a consistent shape, and Clustering is largely shape-based. Moreover, both of these methods are white matter-centric, i.e., based largely on white matter architecture. WMQL, on the other hand, is a gray matter-centric approach that depends primarily on an individual’s cortical architecture.

Figure 2.

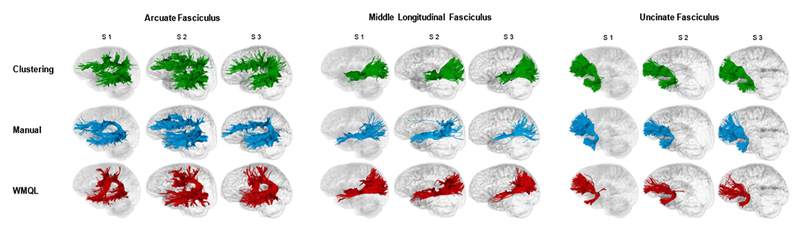
Individual subjects’ white matter tracts displayed with streamline tube visualization in three representative subjects. Data-Driven Groupwise Fiber Clustering tracts are displayed in green, Manual Multiple-ROI Labeling tracts in blue, and White Matter Query Language tracts in red.

S1= Subject 1, S2= Subject 2, S3= Subject 3.

Results from the STAPLE algorithm, a more advanced approach to investigating spatial correspondence across methods, suggest that all three methods were adept at excluding tractography streamlines that almost certainly do not belong to a given tract (true negatives). Clustering had the highest STAPLE sensitivity (true positive) value, signifying that it has high internal consistency, and that it most reliably identified streamline-containing voxels that were included in the output generated by the other two methods. The fact that tracts generated by Clustering encompass the majority of streamlines included in Manual and WMQL tracts, as well as additional streamlines, likely arises because in the Clustering method, streamlines are not constrained to passing through or ending in specific ROIs. Accordingly, the Clustering method will extract streamlines that get excluded from the other methods, for example streamlines on tract peripheries that do not pass through the stem (which may be excluded from the Manual method), streamlines that pass through or end in anatomically “incorrect” regions due to either misregistration or to the tract definition (which may be excluded from WMQL), or shorter streamlines that do not span all ROIs (which may be excluded from both methods). The absence of precise inclusion/exclusion criteria in Clustering can, however, lead to output that is overinclusive: streamlines not strictly considered to belong to a tract of interest (based on the accepted understanding of the tract’s anatomical location and the brain regions it connects) may be included in clustering methods if the streamlines share a similar shape with, and are located proximally to, the tract of interest (e.g. consider fibers of the inferior longitudinal fasciculus and the inferior fronto-occipital fasciculus).

The lower STAPLE sensitivity value for WMQL is driven by a combination of lower spatial agreement with the other methods (corroborated by the Jaccard Coefficient results) and greater tract variability across subjects. This greater inter-subject variability in tract location and shape is expected for a primarily gray matter-centric approach when compared to approaches that are white matter-centric, as gray matter architecture (especially cortical architecture) is more highly variable across individuals, whereas core white matter morphology is generally more consistent. It must additionally be noted that STAPLE metrics are entirely dependent on the tract segmentations input into the algorithm, and therefore output measures are biased to the most consistent spatial representation of a tract, which is not necessarily the most anatomically accurate one.

A more relevant question therefore may be, do the different methods extract white matter tracts with the same anatomical connectivity profiles? Results from the streamline endpoint analysis (Table 6) reveal that connectivity is variable across the methods, with Clustering being more anatomically expansive than the other two methods. Again, this may point to either (or more likely, to both) an overinclusiveness for tracts produced with Clustering, or to the use of inclusionary ROIs that are too restrictive by the other two methods. This analysis emphasizes the importance of understanding which regions of the brain a tract of interest connects, as this has direct implications for anatomical, functional, and clinical interpretation of diffusion MRI tractography results, as well as for the replicability of different studies analyzing the same white matter tract.

White matter tracts are most frequently extracted for the purpose of studying quantitative tract-specific measures, for example structural or scalar measures. Here it is apparent that connectivity variability co-occurs with considerable between-method variability in measures of tract volume and tract length. Significant differences in these measures were pervasive, with no definitive emergent pattern. FA tended to be marginally more reliable across the three methods, with no significant differences arising between FA values derived from Manual and WMQL tracts. Tracts produced by Clustering, however, tended to have significantly higher FA values, potentially due to outlier removal steps that remove irregularly shaped or cluster-inconsistent streamlines (which are most likely to occur on tract peripheries), and due to Clustering’s ability to consistently extract all streamlines that comprise the core of white matter bundles (i.e., streamlines with high FA).

These results demonstrate the various ways in which the choice of white matter delineation method used can affect the tract that is produced and the measures that are derived from it, even when the same input tractography is used. Reciprocally, choices pertaining to which white matter tract to study and which tractography method to employ can also affect the performance of these white matter delineation approaches.

4.1. Impact of white matter tract architecture, image resolution and tractography method on white matter delineation

In this study, spatial and volumetric congruence across methods, assessed by Jaccard Coefficients and Intraclass Correlation Coefficients respectively, were greatest for the UF, followed by the AF, and then the MdLF. Agreement among distinctive white matter delineation methods thereby appears to be influenced by tract shape. Methods may thus more consistently define white matter tracts with unique shapes for which true positive streamlines are more readily distinguished from surrounding linear streamlines—for example the UF, the AF, the cingulum bundle and the fornix—than white matter tracts with long, straight, and radiating or bifurcating fibers—for example the MdLF and the inferior longitudinal fasciculus, the inferior fronto-occipital fasciculus and the corticospinal tract.

Studying tracts with highly variable shape versus variable anatomical connectivity across subjects will also affect individual methods differently. Whereas groupwise fiber clustering methods will potentially perform more poorly when tracts are inconsistently shaped across subjects, especially if larger clusters are used, the accuracy of atlas-based methods will be more affected by diversity in anatomical connectivity as tract definitions may need to be overly inclusive to extract appropriate streamlines from all subjects, or else, to avoid false positives, overly restrictive. Due to their subject specific nature and reliance on identifying bundle cores, manual ROI-based methods should not be affected by such inter-subject variability.

Changes in image acquisition and tractography method will also affect white matter delineation and extraction. Acquiring diffusion images with better spatial resolution and more gradient directions should, in theory, improve the output of all tract delineation methods via improvements in tractography performance. Generating whole-brain tractography with less noise and fewer errors should, for example, increase between-subject consistency, which will improve the implementation of groupwise fiber clustering algorithms. Improved image spatial resolution will also allow for more accurate and specific manual ROI placements, as well as for the tracing of much smaller white matter tracts. Atlas-based methods may derive the greatest benefit from improvements in image quality as in addition to better input tractography, this will allow for enhanced anatomical parcellation accuracy, for parcellations with smaller segmentation regions, and for better atlas to image registration. Additionally, because some atlas-based approaches are conditional on identifying streamlines with endpoints in gray matter ROIs, they are susceptible to failures of tractography to trace streamlines into regions of gray matter. While this concern is largely mitigated by the use of lenient stopping criteria that allow for tracing into gray matter (e.g., minimum FA of 0.15 and GFA of 0.1 (Truong et al., 2014)) and a tractography algorithm that performs well in areas of low anisotropy and high uncertainty, acquisition improvements that allow for greater accuracy at the gray-white boundary will be important for gray matter-centric methods.

The present study cannot provide direct evidence as to how the application of different tractography methodologies would affect results. We postulate however that the use of single rather than multi-tensor tractography would be equally disadvantageous to the three approaches utilized here. Correspondingly, the use of high angular resolution diffusion-weighted imaging (Tuch et al., 2002) based tractography, which has been shown to perform similarly to the algorithm we employed (Baumgartner et al., 2012; Fillard et al., 2011), would most likely yield results from which the same general trends with regards to spatial overlap, tract volume, FA, connectivity, and intra-method consistency would be observed. There are additionally white matter delineation approaches that are not streamline-based, such as probabilistic tractography methods that generate probability heat maps of fiber tract connectivity pathways between brain regions (Behrens et al., 2003; Jbabdi et al., 2007; Parker and Alexander, 2005; Parker et al., 2003), as well as tract segmentation methods that generate 3-dimensional geometric models of white matter structures (Jonasson et al., 2007; Nazem-Zadeh et al., 2011; Rousson et al., 2004; Zhukov, Leonid et al., 2003). Though outside the scope of this study, future studies should resolve whether white matter tract derived measures systematically differ across streamline-based, probabilistic, and segmentation approaches.

Given the non-trivial differences that can arise between conceptually distinct white matter delineation approaches, we offer some suggestions as to how to select an appropriate approach to employ, based on how the strengths and weaknesses of the approach relate to different scientific and clinical contexts.

4.2. Manual Region of Interest-Based Approaches

Past research has demonstrated that manually imposing two or more anatomically specific constraints on tractography input can greatly enhance the precision of white matter tract output (Catani et al., 2002; Huang et al., 2004). This subject-specific approach eliminates the need for registrations, data smoothing, and other data normalization steps that can introduce errors, and the precise drawing of ROIs on a case to case basis ensures that the streamlines being extracted belong to the white matter tract of interest. Consequently, these methods are regarded as the most anatomically accurate, and are used as a basis of comparison during new method validation. In the present study, results (tract volume, tract length, FA, STAPLE sensitivity) derived from the Manual method were generally intermediate between the other two methods, thus manual multiple-ROI methods do appear to serve as a reliable basis for comparison. Nonetheless, these methods have limitations. First, the more conservative use of ROIs in this method can result in false negatives. And second, they require considerable anatomical knowledge and a substantial amount of time, and the placement of ROIs drawn by experimenters can introduce errors or biases. However, a potential alternative to the conventional drawing of manual ROIs is to instead manually place seeds along a white matter tract of interest in order to generate seed-based tractography (e.g. Nazem-Zadeh et al., 2012); this is thought to reduce the time investment and is less dependent on the operator’s anatomical knowledge.

Given the elevated potential for anatomical precision, manual multiple-ROI methods are most apposite for subject-specific analyses (Lazar et al., 2006) and pre-surgical planning (Berman, 2009; Chen et al., 2009; Golby et al., 2011; Pujol et al., 2015; Spena et al., 2010; Yogarajah et al., 2009), wherein delineating an exact representation of a tract is critical. Manual methods should also be utilized in studies involving individuals with deformed or atrophied brains (e.g., Rijken et al., 2015) in which anatomical atlases will not correctly register with diffusion images, and tractography fibers will not be consistently organized across subjects. Studies that include a smaller number of participants and aim to analyze a select number of white matter tracts may consider employing a manual multiple-ROI approach when feasible, particularly those interested in examining stem (core) white matter fibers and their corresponding anatomical features (e.g., tract volume, fiber length, or fiber dispersion (Sotiropoulos et al., 2012)). Previous studies have successfully utilized manual methods to identify abnormalities in white matter tracts in patient populations, for example in the AF in schizophrenia patients experiencing positive symptoms (Psomiades et al., 2016; Seitz et al., 2016), and in the cingulum bundle in individuals with bipolar disorder (Wang et al., 2008). Robust structure-function relationships have also been discovered for white matter tracts extracted with manual methods, for instance, the role of the AF in language-related functions (Maffei et al., 2015).

4.3. Groupwise Fiber Clustering Approaches

Groupwise fiber clustering methods enable the identification and analysis of homologous white matter structures across subjects. Three findings from the present study support that groupwise clustering approaches do extract the most consistent white matter tracts across subjects. First, Clustering consistently produced method-specific tract overlay maps with the greatest volumes (Table 2), signifying the most extensive overlap of tracts across different subjects. Although this may partially result from the fact that the majority of individual tracts produced by Clustering had greater volumes, this finding held for the MdLF, wherein individual Clustering tracts were smallest. Second, Clustering had the highest STAPLE sensitivity value, indicating high within-method spatial consistency. And third, the standard deviations for tract volume, tract length, and FA were lowest for Clustering.

Because groupwise fiber clustering approaches are initially entirely data driven, they avoid a priori anatomical constraints and operator-dependent ROI selection (Voineskos et al., 2009). As seen here, this allows for the inclusion of fibers that ROI-based methods may miss, decreasing the rate of false negatives, but potentially leading to overinclusive results as well. Similar to the lack of ROI use, the use of outlier removal (Guevara et al., 2011; O’Donnell et al., 2016) has both benefits and potential disadvantages. Removing streamlines with low resemblance to nearby clusters (i.e., streamlines that are irregularly shaped, unusual, or uncommon) from the final clustered output reduces the presence of false positives and tractography-associated noise. However, stringent outlier removal may additionally eliminate true positive fibers that deviate from the normal tract trajectory. In other words, seemingly abnormal streamlines may be real, and more aesthetically pleasing tracts may not always be the most anatomically accurate.

Overall, groupwise fiber clustering approaches have the potential to generate very clean bundles, and they facilitate comparisons of relatively uniformly delineated tracts across subjects. Yet, they may limit the ability to identify subtle group differences in structural connectivity. These approaches may therefore be more apposite for studies aiming to minimize variability in tract architecture and volume in order to compare dMRI-derived scalar measures from tracts that are defined consistently across subjects or populations. Groupwise fiber clustering also offers an advanced and unique approach to systematically classifying the entirety of whole-brain tractography, which can be used in whole-brain analyses aimed at studying global white matter features. For example, (Zhang et al., 2017) were able to predict whether an individual had Autism Spectrum Disorder with 78% accuracy by extracting FA and mean diffusivity features from 800 fiber clusters generated from whole-brain tractography.

4.4. Gray and White Matter Atlas-Based Approaches

Atlas-based methods facilitate the extraction of a large number of white matter tracts with clear anatomical connectivity interpretations. The public availability of these methods reduces the need for researchers to have robust neuroanatomical knowledge, thereby increasing the accessibility of performing tract-based dMRI research. Furthermore, the same atlas and tract definitions can be utilized across different studies, increasing reproducibility and the feasibility of comparing results across datasets and across study populations.

Advantageously, automated atlas-based ROI selection eliminates experimenter bias in the drawing of ROIs, yet the ROIs that can be used are limited to those that exist in the atlas. Given that most atlases have relatively large ROIs (e.g. encompassing an entire gyrus), extracting smaller, more anatomically-localized tracts is not feasible unless additional manual segmentations are performed. Large ROIs can furthermore lead to an increased rate of false positives (seen in the present study, for example, between dorsal and ventral portions of the AF). This susceptibility to false positives is further compounded by the possibility of atlas-to- subject misregistrations, which can introduce spurious fibers or variability in tract output. Nevertheless, these methods often make it easy to modify tract extraction instructions when needed (e.g., by changing or constructing new queries in WMQL) so as to produce high quality output, and enhanced registrations can be achieved with the correct combination of registration method (rigid, affine and/or nonlinear) and MR image type (T1-weighted or diffusion images, FA maps and/or DTIs), or by using an anatomical atlas composed of multiple reference anatomies (Suarez et al., 2012).

Atlas-based methods may be generally favorable for the extraction of a large number of white matter tracts from large N datasets, as well as for conducting exploratory connectivity studies, given the ability to create new atlas-based tract extraction instructions. The WMQL method, for example, has been utilized to reveal cortico-striatal degeneration in 191 individuals with prodromal Huntington’s Disease (Shaffer et al., 2017), and to identify tract-based alterations that maximally discriminated individuals with 22q11.2 deletion syndrome from control subjects (Tylee et al., 2017). These methods may furthermore be beneficial for conducting multi-modal analyses that aim to relate dMRI structural connectivity findings to structural, functional, or positron emission tomography MRI findings, as the same anatomical atlas can be utilized across different imaging modalities to localize and relate findings.

5. Conclusions

This comparison of three representative post-tractography white matter tract delineation methods demonstrates that although distinct approaches are able to identify and extract relatively consistent forms of white matter tracts, important differences in tract architecture, connectivity, volume, and mean scalar measures can arise, even when methods rely on the same input tractography and neuroanatomical knowledge. The level of agreement between methods will be influenced by both the specific methodologies being employed, and by the white matter tracts being studied. Careful consideration should therefore be given to decisions regarding which white matter delineation approach to utilize in both research and clinical settings. The future of white matter tract delineation should likely involve methodologies that combine multiple approaches, for example methods that apply multiple manual ROI segmentations to generate multi-reference template atlases (Suarez et al., 2012), or methods that combine initial fiber clustering with subsequent atlas-based white matter classification (Ros et al., 2013; Wassermann et al., 2010; Xu et al., 2013).

Given the present findings, additional future work should be undertaken to investigate the impact that varied white matter delineation approaches have on detecting differences in diffusion measures between groups in typical case-control studies. Elucidating how different approaches ultimately affect the detection of significant results is crucial to study replication and for understanding “case”-associated abnormalities.

6. Limitations

One limitation of this study is that three representative methods were used to exemplify, in turn, a manual multiple ROI-based, an atlas-based, and a groupwise fiber clustering approach, yet not all implementations of these three major approaches will be identical. Nonetheless, methods that can be classified methodologically to one of these three conceptual categories will likely be comparable to the representative methods used in this report. A second limitation arises from the lack of a validated ground truth with regard to white matter fiber tract anatomy. Because the true anatomy of white matter can only be confirmed ex-vivo and post-mortem, we cannot unequivocally determine which method best approximated the true anatomical properties of the white matter tracts under study. Lastly, this analysis was performed using data from 10 healthy participants, thus results may differ in studies of patient populations, especially when pathology interferes with tract anatomy.

Abbreviations:

(ANTS)

Advanced Normalization Tools

(AF)

Arcuate Fasciculus

(dMRI)

Diffusion Magnetic Resonance Imaging

(DTI)

Diffusion Tensor Image

(TE)

Echo Time

(FA)

Fractional Anisotropy

(ICC)

Intraclass Correlation Coefficient

(TI)

Inversion Time

(JC)

Jaccard Coefficient

(MR)

Magnetic Resonance

(MdLF)

Middle Longitudinal Fasciculus

(ROI)

Region of Interest

(ROIs)

Regions of Interest

(TR)

Repetition Time

(STAPLE)

Simultaneous Truth and Performance Level Estimation

(S.D.)

Standard Deviation

(UF)

Uncinate Fasciculus

(UKF)

Unscented Kalman Filter

(WMQL)

White Matter Query Language