Genomic kinship construction to enhance genetic analyses in the human connectome project data

Abstract

Imaging genetic analyses quantify genetic control over quantitative measurements of brain structure and function using coefficients of relationship (CR) that code the degree of shared genetics between subjects. CR can be inferred through self‐reported relatedness or calculated empirically using genome‐wide SNP scans. We hypothesized that empirical CR provides a more accurate assessment of shared genetics than self‐reported relatedness. We tested this in 1,046 participants of the Human Connectome Project (HCP) (480 M/566 F) recruited from the Missouri twin registry. We calculated the heritability for 17 quantitative traits drawn from four categories (brain diffusion and structure, cognition, and body physiology) documented by the HCP. We compared the heritability and genetic correlation estimates calculated using self‐reported and empirical CR methods Kinship‐based INference for GWAS (KING) and weighted allelic correlation (WAC). The polygenetic nature of traits was assessed by calculating the empirical CR from chromosomal SNP sets. The heritability estimates based on whole‐genome empirical CR were higher but remained significantly correlated (r ∼0.9) with those obtained using self‐reported values. Population stratification in the HCP sample has likely influenced the empirical CR calculations and biased heritability estimates. Heritability values calculated using empirical CR for chromosomal SNP sets were significantly correlated with the chromosomal length (r 0.7) suggesting a polygenic nature for these traits. The chromosomal heritability patterns were correlated among traits from the same knowledge domains; among traits with significant genetic correlations; and among traits sharing biological processes, without being genetically related. The pedigree structures generated in our analyses are available online as a web‐based calculator (http://www.solar-eclipse-genetics.org/HCP).

1. INTRODUCTION

International collaborations and biobanks, such as the Human Connectome Project (HCP), are collecting large multimodal datasets to identify genetic and environmental factors that underlie normal and illness‐related variances in the brain and body (Glasser et al., 2013; Van Essen et al., 2013). Genetic analyses use coefficients of relationship (CR) to characterize the degree of shared genetic variance among study participants and partition the phenotypic variance into genetic and environmental sources. Traditionally, CR is approximated based on self‐reported relationships. For example, a pair of individuals may identify themselves as parent and child, siblings, or as cousins. This method requires knowing all relationships among study participants. Self‐reported relatedness values can be inaccurate (e.g., mistaken zygosity in the case of same‐sex twins or mistaken paternity) and this can bias genetic analyses. Alternatively, CR can be measured empirically from high‐throughput genome‐wide single nucleotide polymorphism (SNP) scans (Ramstetter et al., 2017; Toro et al., 2014; Wood et al., 2014; Yang et al., 2010). We hypothesized that empirical CR provides more accurate estimates of shared genetic variance (heritability) than zygosity‐corrected self‐reported values. We tested this hypothesis using the quantitative brain and body measurements collected by the HCP collaboration.

Heritability analyses that model mixed effects divide the phenotypic variance into additive genetic and environmental components in order to quantify the degree of genetic variance. This mixed effect model uses an NxN pedigree matrix of CR (where N is the sample size). Self‐reported CR are calculated as the length of the shortest ancestral path (kindship) between two individuals. Each kinship type is a fixed number that codes the expected degree of shared genomic variance for a kinship type: 1 for the self and a monozygotic twin; ½ for parents, full siblings and dizygotic twins; ¼ for grandparents or half‐siblings; 1/8 for cousins; and 0 for unrelated individuals. However, no two relatives share a fixed number of the genome‐wide genetic polymorphisms (Visscher et al., 2006, 2007), and conversely, seemingly unrelated individuals may share a significant proportion of genetic variance.

CR values can also be inferred empirically by quantifying the similarity in the whole‐genome or chromosomal SNP sets among the study participants. The complex traits used in this analysis are expected to have a highly polygenic architecture, with genetic factors residing on all chromosomes. Traits may share chromosomal heritability patterns due to pleiotropy (directly shared genetic variance) and/or due to similarity in the chromosomal distribution of genes that regulate similar functions. For instance, genetic analyses of hypertension, arterial stiffening and cerebral white matter integrity converged on a 1q24 region that harbors a constellation of genes that code for the cell adhesion protein (SELP, SELL, and SELE) and the coagulation factor V (F5) (Kochunov et al., 2009, 2012; Mitchell et al., 1996; Turner et al., 2005).

We used four empirical CR methods with different normalization approaches. The Kinship‐based INference for Genome wide association study (KING) method was developed to approximate self‐reported CR values. It is frequently used to verify self‐reported relationships in family samples (Manichaikul et al., 2010). In our study, KING was used to verify zygosity for same‐gendered twins. A second method, the Weighted Allelic Correlation (WAC) approach, was developed to study the “missing heritability” of complex phenotypes. The WAC approach produces CR values that are weighted by minor allelic frequency (MAF) using a parameter, α, which is assigned values of 1, −1, or 0 (Speed, Cai, UCLEB Consortium, Johnson, Nejentsev, & Balding, 2017a; Speed, Hemani, Johnson Michael, & Balding David, 2012). A weighting of α = 1 calculates CR by up‐weighting on common variants, whereas a weighting of α = −1 up‐weights CR on the low MAF variants. CR values independent of MAF are calculated using α = 0.

We hypothesized that empirical CR will provide a more accurate assessment of shared genetic variance than the self‐reported values. To test our hypothesis, we chose 17 quantitative traits from four knowledge domains ascertained by HCP: diffusion and structural brain imaging measures, neurocognitive assessments, and physical health. We selected traits based on the expectation of significant heritability and the potential for shared genetic variance across the knowledge domains. Five diffusion traits were analyzed using standard Diffusion Tensor Imaging (DTI) and advanced White Matter Tract Integrity (WMTI) models (Fieremans, Jensen, & Helpern, 2011; Jelescu et al., 2014) to assess the microstructure of cerebral white matter (WM). Structural brain integrity measurements included average gray matter (GM) thickness and regional gray and white matter volumes. We chose four neuropsychological traits consisting of two working memory and two processing speed measurements. In previous research, these traits have shown high heritability and significant genetic correlation with measures of brain integrity (Glahn et al., 2013; Kochunov et al., 2015, 2016). We also considered body mass index (BMI) and systolic and diastolic blood pressures based on research linking body adiposity to cerebral integrity (Kochunov, Glahn, Lancaster, et al., 2011b; Ryan et al., 2017; Spieker et al., 2015).

We tested two hypotheses: (1) Empirical CR derived from whole genome genotyping will provide more accurate heritability measurements than self‐reported CR; and (2) Empirical CR derived from the chromosomal sets of SNPs can be used to probe the polygenic nature of quantitative traits (Visscher et al., 2006, 2007). We show that heritability analyses produce higher estimates of additive genetic variance using empirical rather than self‐reported CR. The chromosomal heritability patterns suggest genes that influence phenotypes with related biological functions may have similar chromosomal distribution patterns of alleles. Our analyses can be extended to other phenotypes using pedigrees we uploaded at http://nitrc.org and the heritability calculator for self‐reported and empirical pedigrees at http://solar-eclipse-genetics.org/HCP.

2. METHODS

2.1. Subjects

Heritability and genetic correlation analyses were performed on data from 1,046 (480/566 M/F) participants in the Human Connectome Project (HCP) for whom scans and data were released (http://humanconnectome.org) after passing the HCP quality control and assurance standards (Marcus et al., 2013). Details of this release are available in the HCP reference manual. The participants in the HCP study were recruited from the Missouri Family and Twin Registry of individuals born in Missouri (Van Essen et al., 2013). All HCP participants were deliberately selected as belonging to young adult sibships of average size 3–4 that include MZ or DZ twin pairs and siblings. Participants ranged in age from 22 to 36 years (average age = 28.7 ± 3.68 years). This age range was chosen because it corresponds to the period when neurodevelopment is largely complete and the onset of neurodegeneration has not yet occurred. The full set of inclusion and exclusion criteria is detailed elsewhere (Van Essen et al., 2013). In short, the HCP subjects are healthy individuals free from major psychiatric or neurological illnesses. They are drawn from ongoing longitudinal studies (Edens, Glowinski, Pergadia, Lessov‐Schlaggar, & Bucholz, 2010; Sartor et al., 2010), where they received extensive previous assessments including history of drug use and emotional and behavioral problems. All subjects provided written informed consent on forms approved by the Institutional Review Board of Washington University in St. Louis.

2.2. Genotyping

The genotyping data for 1,141 subjects were released by HCP and available through the dbGAP repository (https://www.ncbi.nlm.nih.gov/projects/gap/cgi-bin/study.cgi?study_id=phs001364.v1.p1). Briefly, all subjects were genotyped using the Illumina Multi‐Ethnic Global Array (MEGA) SNP‐array that included chip‐specific content from PsychChip and ImmunoChip and provides extended coverage of European, East Asian, and South Asian populations. We used 1,580,642 genotyped SNPs that satisfied the quality control conditions: excluding SNPs with MAF <1%, genotype call rate <95%, and Hardy–Weinberg equilibrium <1 × 10⁻⁶. The genotype data were converted to PLINK file format.

2.3. Quantification of the degree of relationship

SOLAR‐Eclipse uses coefficients of relationship (r _i,j) (equal to twice the coefficients of kinship) to code the probability that two alleles from individuals i and j are identical by descent. The coefficient of relationship is a function of identity by descent sharing statistics, r _i,j = π_1i,j/2 + π_2i,j, where, π_1i,j and π_2i,j are the probabilities that two individuals share one and two alleles through a common ancestry.

Self‐reported coefficients of relationship between individuals i and j are calculated as r _i,j = 1/2ⁿ where n is the length of the ancestral path that connects them. Common n values include n = 1 for parents, full siblings, and dizogotic twins; n = 2 for grandparents, half‐siblings; n = 3 for cousins; and increasing n values for more distance relatives. Unrelated individuals assumed to share no ancestral variance and are coded with CR = 0. The self‐reported CR coefficients may be subject to mistaken zygosity for same sex twins. Therefore, we used zygocity corrected self‐reported CR values to verify twin zygosity using the Robust‐KING empirical CR method.

Empirical r _i,j were calculated using the methods implemented in SOLAR‐Eclipse software (http://www.solar-eclipse-genetics.org). The empirical_pedigree function takes the allelic data stored in a PLINK file as an input and produces a pedigree file. All empirical methods infer r _i,j based on the average identity by state statistics while weighting the result by sample‐level allele frequency at each SNP. We calculated four empirical pedigrees using two methods: robust Kingship based INference for Genome‐wide studies (robust‐KING) (Manichaikul et al., 2010) and weighted allelic correlation (WAC) (Hayes, Visscher, & Goddard, 2009).

2.3.1. Robust‐KING

The robust KING method was developed for fast r _i,j calculations in familial samples. The method is described in details in the original publication (Manichaikul et al., 2010). Briefly, the coefficients of relatedness are calculated using Equation (1).

$$r_{i,j}=1-\frac{N_{\mathit{Aa}}^i+N_{\mathit{Aa}}^j}{2N_{\mathit{Aa}}^i}+\frac{N_{\mathit{Aa},\mathit{Aa}}-2N_{\mathit{AA},\mathit{aa}}}{N_{\mathit{Aa}}^i}$$ (1)

where, $N_{\mathit{Aa}}^{i,j}$ is the total number of heterozygotes for the ith and jth individuals, and N _Aa,Aa and N _AA,aa are the total number of SNPs at which both individuals of the pair are hetero‐ and homozygous. The KING method is computationally efficient because the N coefficients are computed using binary logic operations (AND and OR).

2.3.2. Weighted allelic correlation

The weighted allelic correlation (WAC) approach (Hayes et al., 2009) calculates the coefficient of relationship using the correlation coefficient among the allelic scores and weighting it by the minor allele frequency factor: p(1 − p)^α using Equation (2).

$$r_{i,j}=\frac{1}{N}\sum _{n=1}^N\left(G_{i,n}-2p_n\right)\left(G_{j,n}-2p_n\right){\left(p_n\left(1-p_n\right)\right)}^{\alpha }$$ (2)

where, G _i,n and G _j,n are the allelic scores (0, 1, or 2) for the nth SNP for the ith and jth individuals, p _n is the minor allele frequency (MAF) for the SNP calculated for the sample, and N is the total number of SNPs. The parameter α determines the weightings of the coefficient of relationship proportional to MAF (α > 0), irrespective of MAF (α = 0), and inversely proportional to MAF (α < 0). We calculated the pedigree matrix for three common settings α = 1, 0, and −1. The setting of 1 up‐weights CR on the similarity in common alleles; the setting of −1 up‐weights CR on similarity in rare alleles; and a setting of 0 calculates CR independent of allelic frequency.

2.4. Quantitative traits

We selected traits from four domains: diffusion, structure, neuropsychology and physiology (Table 1). The traits within each domain were chosen based on the expected correlation among the traits within and across the domains. Diffusion weighted imaging (DWI) traits were calculated using standard diffusion tensor imaging (DTI) and White Matter Tract Integrity (WMTI) models. All other traits were obtained from the public section of the HCP database (db.http://humanconnectome.org). The structural traits included whole‐brain average gray mater (GM) thickness, whole‐brain and cortical GM volume, and whole brain white matter (WM) volume computed from FreeSurfer 5.3 analyses of high resolution (0.7 mm isotropic) T1w and T2w scans. Four neuropsychological traits were chosen to be sensitive to cognitive processing speed and working memory. Working memory performance was assessed using accuracy scores on the list sorting (Accuracy working memory) and dimensional change card sort (Card Sorting) tasks. Processing speed was assessed using the Pattern Completion Processing Speed from the NIH Toolbox (http://www.nihtoolbox.org) (Carlozzi, Tulsky, Kail, & Beaumont, 2013) and reaction time (Barch et al., 2014). Physiological traits included body mass index (BMI) and systolic and diastolic blood pressure (BPSys, BPDias) (Table 1).

Table 1.

Heritability values (±standard error) for quantitative traits from four knowledge domains ascertained by HCP calculated using self‐reported and empirical coefficients of relationship

Traits	Trait description	Heritability (h2) estimates
Diffusion domain		Self‐reported	KING	WAC α = 1	WAC α = 0	WAC α = −1
AWF	Axonal water fractions calculated using WMTI model	0.91 ± 0.02 (p < 10−26)	0.91 ± 0.01 (p < 10−26)	0.93 ± 0.01 (p < 10−26)	0.94 ± 0.01 (p < 10−26)	0.96 ± 0.01 (p < 10−26)
DKI‐FA	Fractional anisotropy of water diffusion (FA) calculated using white matter tract integrity (WMTI) model (fits diffusion and kurtosis tensor)	0.85 ± 0.02 (p < 10−26)	0.86 ± 0.02 (p < 10−26)	0.89 ± 0.02 (p < 10−26)	0.92 ± 0.01 (p < 10−26)	0.93 ± 0.02 (p < 10−26)
DTI‐FA	Fractional anisotropy of water diffusion (FA) calculated using diffusion tensor model (fits diffusion tensor only)	0.86 ± 0.02 (p < 10−26)	0.85 ± 0.02 (p < 10−26)	0.88 ± 0.02 (p < 10−26)	0.91 ± 0.02 (p < 10−26)	0.94 ± 0.02 (p < 10−26)
KA	Kurtosis anisotropy calculated from the WMTI model	0.86 ± 0.02 (p < 10−26)	0.87 ± 0.02 (p < 10−26)	0.90 ± 0.02 (p < 10−26)	0.91 ± 0.01 (p < 10−26)	0.94 ± 0.02 (p < 10−26)
TORT	Tortuosity of the extra cellular space calculated using WMTI model	0.79 ± 0.02 (p < 10−26)	0.77 ± 0.03 (p < 10−26)	0.82 ± 0.03 (p < 10−26)	0.85 ± 0.02(p < 10−26)	0.90 ± 0.03 (p < 10−26)
Structural imaging domain
GM thickness	Average thickness of cortical gray matter (GM) ribbon	0.80 ± 0.02 (p < 10−26)	0.80 ± 0.03 (p < 10−26)	0.83 ± 0.02 (p < 10−26)	0.85 ± 0.02 (p < 10−26)	0.88 ± 0.02 (p < 10−26)
Cortical GM volumes	Volume of cortical GM	0.93 ± 0.01 (p < 10−26)	0.97 ± 0.02 (p < 10−26)	0.96 ± 0.03 (p < 10−26)	0.99 ± 0.01 (p < 10−26)	0.99 ± 0.02 (p < 10−26)
GM volume	Volume of cerebral GM	0.93 ± 0.01 (p < 10−26)	0.98 ± 0.02 (p < 10−26)	0.99 ± 0.01 (p < 10−26)	0.99 ± 0.01 (p < 10−26)	0.99 ± 0.01 (p < 10−26)
WM volume	Volume of cerebral WM	0.94 ± 0.01 (p < 10−26)	0.95 ± 0.01 (p < 10−26)	0.95 ± 0.01 (p < 10−26)	0.96 ± 0.01 (p < 10−26)	0.94 ± 0.01 (p < 10−26)
Body physiology domain
BMI	Body mass index	0.72 ± 0.04 (p = 10−26)	0.73 ± 0.04 (p < 10−26)	0.76 ± 0.04 (p < 10−26)	0.78 ± 0.03 (p < 10−26)	0.82 ± 0.01 (p < 10−26)
BP sys	Systolic blood pressure	0.40 ± 0.05 (p = 10−12)	0.40 ± 0.05 (p = 10−13)	0.45 ± 0.06 (p = 10−14)	0.48 ± 0.06 (p = 10−15)	0.56 ± 0.06 (p = 10−16)
BP Dias	Diastolic blood pressure	0.46 ± 0.05 (p = 10−16)	0.50 ± 0.05 (p = 10−17)	0.56 ± 0.05 (p = 10−18)	0.59 ± 0.05 (p = 10−18)	0.65 ± 0.06 (p = 10−19)
Neurocognitive domain
Accuracy‐WM	Accuracy scores on the list sorting working memory task	0.53 ± 0.04 (p < 10−26)	0.51 ± 0.04 (p < 10−26)	0.49 ± 0.00 (p < 10−26)	0.57 ± 0.05 (p < 10−26)	0.65 ± 0.05 (p < 10−26)
Reaction time	Reaction time measured in the attention task	0.41 ± 0.06 (p = 10−12)	0.40 ± 0.06 (p = 10−11)	0.43 ± 0.06 (p = 10−13)	0.47 ± 0.06 (p = 10−14)	0.60 ± 0.06 (p = 10−15)
Processing speed	Pattern completion processing speed scores	0.38 ± 0.06 (p = 10−11)	0.35 ± 0.06 (p = 10−10)	0.39 ± 0.06 (p = 10−14)	0.42 ± 0.06 (p = 10−15)	0.51 ± 0.07 (p = 10−16)
Picture sequence	Scores on the picture sequence working memory task	0.50 ± 0.05 (p = 10−21)	0.52 ± 0.04 (p < 10−26)	0.55 ± 0.05 (p < 10−26)	0.58 ± 0.05 (p < 10−26)	0.65 ± 0.05 (p < 10−26)
Card sorting	Scores of the dimensional change card sort task	0.40 ± 0.06 (p = 10−12)	0.45 ± 0.05 (p = 10−15)	0.49 ± 0.06 (p = 10−16)	0.53 ± 0.05 (p = 10−17)	0.64 ± 0.05 (p = 10−19)

2.4.1. Diffusion data collection and preprocessing

Diffusion data was collected at Washington University St. Louis using a customized Siemens Magnetom Connectome 3 Tesla scanner with a 100 mT/m maximum gradient strength and a 32‐channel head coil. Details on the scanner, image acquisition and reconstruction are provided elsewhere (Ugurbil et al., 2013) and found online at https://www.humanconnectome.org/study/hcp-young-adult/document/1200-subjects-data-release). Briefly, diffusion data were collected using a single‐shot, single refocusing spin‐echo, echo‐planar imaging sequence with 1.25 mm isotropic spatial resolution (TE/TR = 89.5/5,520 ms, FOV = 210 × 180 mm). Three gradient tables of 90 diffusion‐weighted directions and six b = 0 images each, were collected with right‐to‐left and left‐to‐right phase encoding polarities for each of the three diffusion weightings (b = 1,000, 2,000, and 3,000 s/mm²). The total imaging time for collection of diffusion data was approximately 1 hr.

Diffusion data were preprocessed using a modified HCP Diffusion pipeline (Glasser et al., 2013; Sotiropoulos et al., 2013). The pipeline first corrected for thermal noise by applying the Marchenko–Pastur Principle Component Analysis (MPPCA) (Veraart, Fieremans, Jelescu, Knoll, & Novikov, 2016a; Veraart, Fieremans, & Novikov, 2016b; Veraart, Novikov, et al., 2016c), and was followed by the normalization of b0 image intensity across runs. Corrections for Gibbs ringing (Kellner, Dhital, Kiselev, & Reisert, 2016) and Rician bias (Gudbjartsson & Patz 1995) were applied as well as corrections for EPI susceptibility and eddy‐current‐induced distortions, gradient‐nonlinearities, and subject motion. Lastly, a brain mask was applied.

2.4.2. Diffusion data modeling

Diffusion data were analyzed using two approaches: a standard diffusion tensor fitting and an advanced White Matter Tract Integrity model. Standard DTI‐Fractional anisotropy (FA) values were obtained by fitting the diffusion tensor model (first two terms in Equation (3)) using the FSL‐FDT toolkit (Behrens et al., 2003). WMTI is an extension of DTI that uses a model‐independent diffusion kurtosis signal representation and the kurtosis term to account for non‐Gaussian behavior of the diffusion signal (Equation (3)) (Jensen & Helpern 2010; Jensen, Helpern, Ramani, Lu, & Kaczynski, 2005; Lu, Jensen, Ramani, & Helpern 2006). WMTI derives both the diffusion and kurtosis tensors using the second‐order expansion of the multi b‐shell diffusion‐weighted signal decay as a function of the b‐value:

$$\ln S\left(b,\mathit{g}\right)\mathbf{=}\ln S\left(0\right)-b\sum _{i,j=1}^3{g}_i{g}_j{D}_{\mathit{ij}}+\frac{b^2}{6}{\left(\sum _{i=1}^3\frac{D_{\mathit{ii}}}{3}\right)}^2\sum _{i,j,k,l=1}^3{g}_i{g}_j{g}_k{g}_l{W}_{\mathit{\text{ijkl}}}+O\left(b^3\right)$$ (3)

where, g _i is the ith component of gradient direction g and S(0) is the nondiffusion‐weighted signal intensity. D _ij is the ijth element of the fully symmetric diffusion tensor D, characterized by six independent elements and W _ijkl denotes an element of the diffusion kurtosis tensor W, which is fully parameterized by 15 independent elements. During the WMTI fit, multivariate regression was used to estimate the eigenvalues for the diffusion (L_1,2,3) and kurtosis (K_1,2,3) tensors. The three eigenvalues for the diffusion tensor were converted to axial (L_║), radial, (L_⊥), and DKI‐FA. Similarly, the three eigenvalues of the kurtosis tensor were converted to axial (K_║), radial, (K_⊥), and kurtosis anisotropy (KA) values (Poot, den Dekker, Achten, Verhoye, & Sijbers, 2010). WMTI calculates two additional parameters: axonal water fractions (AWF) and tortuosity of the extra‐axonal space (TORT), Equations (4) and (5)

$$\mathrm{AWF}=\frac{K_{\max }}{K_{\max }+3}$$ (4)

$$\text{TORT}=\frac{D_{e,\Vert }}{D_{e,\perp }}$$ (5)

AWF is hypothesized to constitute the fraction of diffusion signal that originates from intra‐axonal water. K _max is the maximum kurtosis along all directions, and D _e,║ and D _e,⊥ are the apparent axial and radial diffusivities of the extra‐axonal space (Ades‐Aron et al., 2018; Jelescu et al., 2014).

Whole‐brain average diffusion parameters were obtained using the ENIGMA‐DTI protocol (https://www.nitrc.org/projects/enigma_dti) (Jahanshad et al., 2013). Briefly, DTI‐FA images were nonlinearly registered to the ENIGMA‐DTI target brain using FSL's FNIRT (Jahanshad et al., 2013). This target was created as a “minimal deformation target” based on images from the participating studies as previously described (Jahanshad et al., 2013). The data was processed using FSL's tract‐based spatial statistics (TBSS; http://fsl.fmrib.ox.ac.uk/fsl/fslwiki/TBSS) analytic method (Smith et al., 2006) that was modified to project individual FA values onto the hand‐segmented ENIGMA‐DTI skeleton mask. The DTI‐FA projection maps were used to project DKI‐FA, KA, AWF, and TORT maps onto the skeleton to ensure that all values corresponded to the same voxels. The whole‐brain average traits were calculated by averaging values across the skeleton.

2.5. Heritability and genetic correlation: Analysis of additive genetic variance and covariance

Heritability (h ²) is the proportion of the total phenotypic variance (σ _P ²) that can be explained by the genetic effects of genes (σ _g ²), Equation (6).

$$h^2={\sigma }_g^2/{\sigma }_P^2.$$ (6)

SOLAR‐Eclipse's heritability calculations are accelerated using the Fast Permutation Heritability Inference (FPHI) approach (polygenic –fphi command). It uses a single step estimation to produce an asymptotically unbiased estimate (Ganjgahi et al., 2015). The FPHI provides a significant (10³) computational acceleration relative to the standard iterative maximum likelihood estimation in SOLAR‐Eclipse.

We used a bivariate genetic analysis to calculate the magnitude and significance of the genetic correlation coefficient (ρ _G). ρ _G corresponds to the proportion of variability that results from shared additive genetic effects. The overall phenotypic correlation (ρ _P) between two traits (represented by A and B in Equation (7)) is equal to ρ _G and the residual correlation (ρ _E) that represents shared environmental effects.

$${\rho }_P=\sqrt{h_A^2}\sqrt{h_B^2}\cdot {\rho }_G+\sqrt{1-h_A^2}\sqrt{1-h_B^2}\cdot {\rho }_E$$ (7)

where, h² _A and h² _B denote the heritability for each of the traits. If ρ _G is significantly different from zero, then a significant proportion of the variance in two traits results from the shared genetic factors (Almasy, Dyer, & Blangero, 1997). All genetic analyses were conducted with age, sex, age*sex, age², and age² * sex included as covariates.

2.6. Chromosomal heritability estimates

We partitioned the genotyping data into individual chromosomes to examine the distribution of empirical heritability across the genome. We estimated the coefficients of relationship using SNPs from each autosomal chromosome (22 in total) and used pedigree matrices constructed from these coefficients to estimate the empirical heritability. We excluded sex chromosomes due to gender differences.

3. RESULTS

3.1. Empirical versus self‐reported coefficients of relationship

The scatter plots of the empirical and self‐reported coefficients of relationship (off‐diagonal elements) are shown in Figure 1. The KING approach faithfully approximated the average coefficients of relationship: 0.99 ± 0.001 for identical twins (zygosity‐corrected self‐reported coefficient = 1.0); 0.50 ± 0.02 for fraternal twins/siblings (zygosity‐corrected self‐reported coefficient = 0.5); and 0.25 ± 0.04 for half‐siblings (self‐reported coefficient = 0.25). The KING coefficients showed a slight negative bias (−0.05 ± 0.05) for the unrelated individuals (self‐reported coefficient = 0). The correlation between KING and self‐reported coefficients was positive and significant r ² = 0.95 (p < 10⁻¹⁰).

Figure 1.

Scatter plot of coefficients of relationship (CR) obtained using empirical approaches versus self‐reported values (off‐diagonal elements only). The linear fit between empirical and self‐reported parameter was characterized by intercept (a), slope (b) and the correlation coefficient squared (r ²)

The relationship coefficients calculated by WAC, under the three different situations, were lower than the self‐reported values. For identical twins, the coefficients of relationship were 0.79 ± 0.05, 0.70 ± 0.09, and 0.65 ± 0.20 for α = 1, 0, and −1, respectively. For fraternal twins/siblings the coefficients were 0.48 ± 0.06, 0.43 ± 0.08, and 0.40 ± 0.10 for α = 1, 0, and −1. For half‐siblings, these coefficients were 0.31 ± 0.05, 0.31 ± 0.09, and 0.26 ± 0.10 for α = 1, 0, and −1. The coefficients for unrelated individuals had a zero bias with standard deviation of 0.05, 0.05, and 0.06 for α = 1, 0, and −1.

The highest correlation between empirical and self‐reported relationships were observed for WAC α = 1 (r ² = 0.98, p < 10⁻¹⁰), followed by α = 0 (r ² = 0.97, p < 10⁻¹⁰). The lowest was observed for WAC α = −1 (r ² = 0.74, p < 10⁻¹⁰).

3.2. Heritability

Heritability estimates calculated using self‐reported and empirical coefficients are shown in Table 1 and Figure 2. Heritability estimates using the empirical relationship, as a group, were significantly higher than those derived from self‐reported relationships (anova p = .001). The average heritability for all traits was h ² = 0.71 ± 0.22, 0.73 ± 0.23, 0.75 ± 0.22, 0.77 ± 0.21, and 0.81 ± 0.17 for self‐reported, KING, and WAC α = 1, 0, and −1, respectively (Figure 2).

Figure 2.

Scatter plot of heritability values calculated using empirical relationship (CR) versus these obtained from self‐reported CR, including linear fit lines, equations, and correlation coefficients

When compared with self‐reported coefficients, WAC α = −1 showed a significant 15% increase in heritability estimates (p = 10⁻⁸). The KING approach also provided heritability estimates that were 1.5% higher than those obtained using the self‐reported coefficients (p = .04). The pattern of heritability values was consistent for all approaches (r ² > 0.98) with similar standard errors (Figure 2).

3.3. Genetic correlation

Genetic correlation results for the phenotypic (ρ _P), genetic (ρ _G), and environmental (ρ _E) correlation coefficients are shown for the zygosity‐corrected self‐reported coefficients in Figure 3. The genetic correlation results for all four empirical approaches were similar to self‐reported pedigree results (r ² > 0.95) and therefore not shown. We observed significant correlation patterns for within‐domain correlations. Notable observations include significant correlations for FA values calculated using DTI and WMTI (ρ_P = 0.89, ρ_G = 0.91, ρ_E = 0.89, all p < 10⁻⁶) and strong correlations between DTI‐FA and KA (ρ_P = 0.82, ρ_G = 0.89, and ρ_E = 0.57).

Figure 3.

The phenotypic (ρ _p), left, genetic (ρ _G), center, and environmental (ρ _E), right, correlation coefficients calculated among the quantitative traits [Color figure can be viewed at http://wileyonlinelibrary.com]

3.4. Chromosomal heritability estimates

Heritability estimates using coefficients of relationship calculated for each of the 22 chromosomes using the WAC approach are shown in Figure 4. The heritability values were highest for WAC α = −1 (p < .01). The average heritability values for all 17 traits were significantly correlated with the chromosomal length (r = 0.76, 0.70, and 0.55, p < .01 for α = 1, 0, and −1) (Figure 4, bottom graph).

Figure 4.

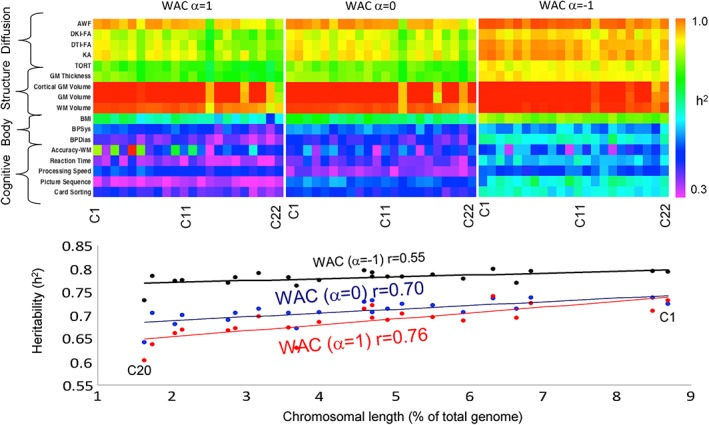
Heritability estimates (top panel) calculated for chromosomal SNPs showed significant dependence on the length of the chromosome [Color figure can be viewed at http://wileyonlinelibrary.com]

Partial correlation analysis was used to calculate bivariate correlations for 22 chromosomal heritability values among the 17 traits, while correcting for the chromosomal length (Figure 5). This analysis tested the similarities in variances that are explained by the genetic variability encoded by each of the chromosomes. The patterns produced by this analysis were significantly correlated for off diagonal elements among the three α weighting values (all r > 0.80, all p < 10⁻⁵). The pattern of chromosomal correlation values was not correlated with phenotypic, genetic, or environmental correlation patterns (all r < 0.10, all p > .3). They replicated significant within‐domain correlations (Figure 5). They also showed that some traits with hypothetically overlapping biological function, such as white matter volume and diffusion domain measurements, had a significant similarity in the chromosomal heritability patterns in the absence of significant phenotypic or genetic correlations between them (Figure 5). Heritability estimates for the chromosomal pedigrees were not available for the KING approach due to numerical failures of chromosomal heritability estimates.

Figure 5.

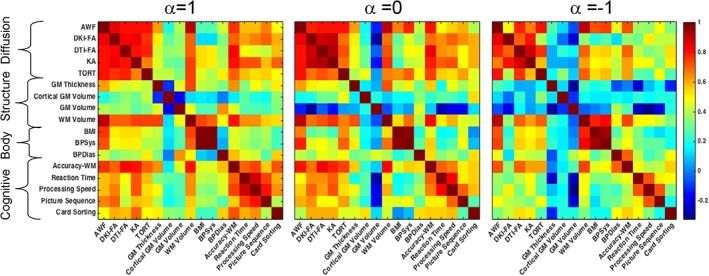
The partial correlation coefficients calculated for chromosomal weighted allelic correlation (WAC) heritability patterns while correcting for chromosomal length. The partial correlation maps show significant within and across domains similarity in heritability patterns for traits that encode measurements with overlapping biology such as the white matter volume (WM) and the diffusion domain measurements [Color figure can be viewed at http://wileyonlinelibrary.com]

4. DISCUSSION

The empirical coefficients of relationship (CR) derived from high‐density genome scans may improve heritability estimates in the complex phenotypes collected by the Human Connectome Project (HCP). We used four empirical CR approaches and 17 quantitative traits selected from the four knowledge domains collected by the HCP. We observed that heritability values calculated using empirical CR values were highly correlated with heritability estimates obtained using self‐reported CR. The weighted allelic correlation (WAC) approach that up‐weighted CR coefficients based on sharing of low MAF alleles (α = −1) produced higher heritability estimates. This may suggest that the variance in complex neuroimaging, neuropsychological and body health traits is influenced by low MAF alleles or that the low frequency variants may provide more informative CR. However, post‐hoc analyses showed that the WAC α = −1 approach was more sensitive to the ancestral/ethnic differences in this mixed sample which may have biased heritability estimates. Heritability estimates obtained using chromosomal CR were correlated with the length of the chromosome (r > 0.5), suggesting the highly polygenetic inheritance mechanism expected for complex traits. The patterns of chromosomal heritability estimates for the HCP traits suggested that genes that influence phenotypes with closely related biological functions, such as brain volume and axonal geometry, might have a similar chromosomal distribution of alleles. The heritability calculator for self‐reported and empirical pedigrees is available online (http://solar-eclipse-genetics.org/HCP) and the pedigrees are shared via http://nitrc.org.

Inferring relatedness in family samples, such as HCP, is an essential component of imaging genetic analyses. We compared the relatedness estimates for four empirical CR approaches and found them to be highly correlated with the self‐reported CR values (r = 0.86–0.99). The Kinship‐based INference for Gwas (KING) approach was developed to approximate self‐reported CR in family samples. This method faithfully matched the self‐reported CR values in relatives but showed a negative bias (average CR = −0.05) for unrelated individuals (expected CR = 0). In other studies, this approach was 92–99% accurate in estimating relatedness in first‐ to third‐degree relatives, but likewise showed a negative bias (underestimating relatedness) in more distant relatives, due to deviations from the Hardy–Weinberg approximation (Ramstetter et al., 2017; Visscher et al., 2007).

Here, we used empirical CR methods that were developed for performing SNP‐based heritability analyses in unrelated samples and implemented in LDAK(Speed, Cai, UCLEB Consortium, Johnson, Nejentsev, & Balding 2017b) and GCTA (Visscher et al., 2006, 2007). SNP‐based heritability analyses are usually performed in unrelated individuals where relatives (CR > 0.025) are routinely removed. The rational for removing related individuals from the samples of mainly unrelated individuals was to prevent potential biases due to shared environment and instead focus on the variance explained by common genetic variants. The empirical CR pedigree estimates the genetic relatedness among a set of individuals and is appropriate for both unrelated and related individuals (Zaitlen et al., 2013). The SNP‐heritability analysis in a related sample changes the inference to favor the estimated total additive genetic variance (from both common and rare sources). The use of related individuals leads to a more statistically powerful inference of total additive genetic variance as demonstrated in this study, where the empirical heritability estimates were similar or higher than these obtained using self‐reported values.

CR calculated using the weighted allelic correlation (WAC) method showed lower correlation with self‐reported values when the weighting emphasis shifted from alleles with common to lower MAF (r = 0.99, 0.98, and 0.86 for α = 1, 0, and −1). All WAC approaches showed zero bias for unrelated subjects (average CR = 0.00). The CR values calculated using the WAC approach were sensitive to the ethnicity of the HCP sample. Post‐hoc analyses were performed to investigate the break in distribution in CR coefficients that was most apparent for the α = −1 setting (Figure 1). The variance in the WAC α = −1 CR values for monozygotic twins was significantly affected (adjusted r = 0.80) by the variance captured by the distance in four genetic clusters calculated using the multidimensional scaling analysis. This dependence was lower but significant for both WAC α = 0 and 1 (adjusted r ² = 0.70 and 0.57, respectively). In all instances, genetic cluster 1 scores showed the greatest explained variance in CR and were significant for all three α settings. Multidimensional scaling scores for clusters 2 and 3 were significant for α = −1, while cluster 3 scores were significant for α = 0. Multidimensional scaling analysis captures the “genetic distance” between subjects and is sensitive to population stratification in ethnically diverse samples such as the HCP. The variance in multidimensional scaling scores was not significantly correlated with the traits and repeating heritability analyses with the scores included as covariates produced no difference in outcome.

Empirical CR approaches produced higher heritability values than these obtained using self‐reported CR. The KING method produced an approximately 1.5% improvement over zygosity‐corrected self‐reported data. Higher h ² values were seen with increased weighting on the low MAF (0.5% < MAF < 10%) SNPs with the highest heritability estimates for the WAC α = −1 method. This may suggests that the phenotypic variance in complex traits may be linked to lower rather than higher MAF variants (Speed et al., 2017a). It may also suggest that ethnic differences in the sample may bias the heritability estimates produced using the empirical CR calculated WAC approach. We observed a high (r > 0.90) correlation between measurements of the shared genetic and environmental variance among the traits. The partitioning of shared phenotypic variance is the function of joint heritability. The heritability values were highly correlated between empirical and self‐reported approaches and therefore the results of the genetic correlation analyses were similar for all methods.

We observed significant genetic correlation among the traits within each of the domains. All the traits within the diffusion domain were highly inter‐correlated for both genetic and environmental estimates. This included high genetic (ρ _G = 0.81, p < 10⁻¹⁰) correlation between fractional anisotropy (FA) calculated using DTI and WMTI, despite the differences in the underlying models. Likewise, all structural volumetric measurements showed high genetic correlations (all ρ _G > 0.70, all p < 10⁻³). However, cortical GM thickness showed only modest genetic correlation with cortical GM and WM volumes (ρ _G = 0.31 and 0.20, p < .001), replicating previous observations (Winkler et al., 2010). BMI showed the expected shared genetic variance with both systolic (ρ _G = 0.60, p < 10⁻⁹) and diastolic (ρ _G = 0.48, p < 10⁻⁷) blood pressure (Figure 3). Significant genetic correlation was observed between the scores of working memory tests (Accuracy and Picture Sequencing ρ _G = 0.62, p < 10⁻¹⁰; Accuracy and Card Sorting ρ _G = 0.63, p < 10⁻¹⁰) and processing speed and reaction time (ρ _G = −0.62, p < 10⁻¹⁰) despite the differences in the measurement procedure: that is, computer test versus fMRI experiment (Figure 3). The genetic correlations between traits from different domains were sparse. We replicated a significant correlation between FA and Processing speed (ρ _G = 0.44 and 0.34, p < 10⁻⁶ for FA measured using DTI and WMTI approaches) and FA and reaction time (ρ _G = −0.27 and −0.22, p < .01) (Kochunov et al., 2010, 2015). Likewise, we replicated a significant negative correlation between BMI and KA (ρ _G = −0.22, p = .0001) (Ryan et al., 2017). We also observed previously reported significant genetic correlation between DTI‐FA and WMTI‐KA values (ρ _G = 0.21 and 0.22, p < .0001) (Kochunov, Glahn, Nichols, et al., 2011a).

Heritability analyses were repeated using CR calculated for each autosomal chromosome. The highest average h ² values were again observed for the WAC α = −1 method. There was a positive correlation between the length of the chromosome and the h ² values derived from its CR matrix. The correlation with chromosomal length was numerically higher for an α weighting that emphasized similarity on common alleles (r = 0.76 vs. 0.55 for α = 1 and −1, respectively), but this difference was not significant (p > .1). There were strong similarities in the patterns of per‐chromosome h² values for some traits (Figure 5). The chromosomal h² correlation matrix was visually similar but uncorrelated with the patterns of genetic and environmental correlations. Traits with significant genetic correlation showed strong correlation with chromosomal h² values. Traits from overlapping biological functions had highly correlated chromosomal heritability patterns even in the absence of genetic or environmental correlation. For instance, the axonal water fraction (AWF) and WM volumes showed a significant (r = 0.92, p < 10⁻⁸) correlation between chromosomal heritability patterns in the absence of significant genetic or environmental correlations (ρ _G = 0.08, p = .08; ρ _E = 0.03, p = .7). The processing speed and reaction times showed heritability patterns that overlapped with cognitive, diffusion and structural traits, yet there was no overlap with the heritability patterns for BMI or blood pressure. Overall, the chromosomal data indicates that the genetic architecture of complex quantitative traits is reflected by similarity for low MAF SNPs, where the density of the loci may also vary across chromosomes.

5. LIMITATIONS

Empirical CR methods have biological limitations. All four of the empirical methods we evaluated produced negative CR. The negative CR reflect violations of Hardy–Weinberg equilibrium such as ancestral differences in linkage disequilibrium structures, overlapping generations and deviations from the assumption on the constancy of genotype frequencies in a population (Visscher et al., 2007). We retained negative CR in the analysis because selecting a threshold for empirical CR may bias the likelihood calculations (Visscher et al., 2007). Empirical CR values may vary by both the calculation method and the genotyping approach and this may alter heritability results. We show that heritability and genetic correlation patterns had a high (r > 0.9) correlation regardless of the CR approach, which suggests the high overall reproducibility of these analyses.

Empirical CR should be used with caution in ethnically diverse samples due to their sensitivity to population stratification along the ethnic background. We observed that CR calculated using the WAC approaches were sensitive to the ethnicity‐related genetic distance among HCP subjects. HCP is a multiethnic sample and genetic distance among the subjects calculated using a multidimensional scaling approach explained significant variance in the CR. The association was the highest for the WAC α = −1 approach that up‐weighted CR estimates on the low minor allele frequency variants. This has likely biased the pedigree matrix and led to higher heritability values by incorporating ethnicity‐specific genetic distance in the calculation of additive genetic variances.

Empirical CR methods also have methodological limitations. The empirical CR matrix is more densely populated than the self‐reported matrix thus increasing (by a factor of 10–20) the computational time for the classical maximum likelihood methods. The computation time remained the same for FPHI while producing an accurate approximation of h ² values (within 1–3%). Another methodological limitation was convergence issues in chromosomal CR values produced by the KING approach which prevented the use of these values in the analyses. This convergence issue was observed during the inversion of the chromosomal CR matrix in both the classical ML and FPHI methods.

6. CONCLUSIONS

We compared heritability calculations based on empirically measured genetic variance among participants in HCP and observed them to be significantly higher than those calculated using self‐reported CR. The highest h ² values were observed for the CR method that weighted on the sharing of low‐MAF alleles. However, the population stratification caused by ethnic differences among subjects has likely biased this approach and produced higher heritability estimates. Nonetheless, the heritability values were highly correlated between empirical and self‐reported CR. The genetic correlation pattern mirrored the pattern of shared phenotypic variance and was similar across all CR methods. Empirical CR values can be calculated for whole‐genome or individual chromosomes. Further research may focus on heritability estimates calculated for specific SNP sets such as these selected for protein coding genes and regulatory regions. The heritability values for HCP traits can now be computed using self‐reported and empirical pedigrees online at http://www.solar-eclipse-genetics.org/HCP

Kochunov P, Donohue B, Mitchell BD, et al. Genomic kinship construction to enhance genetic analyses in the human connectome project data. Hum Brain Mapp. 2019;40:1677–1688. 10.1002/hbm.24479