Physical determinants of the self-replication of protein fibrils

Abstract

The ability of biological molecules to replicate themselves, achieved with the aid of a complex cellular machinery, is the foundation of life. However, a range of aberrant processes involve the self-replication of pathological protein structures without any additional factors. A dramatic example is the autocatalytic replication of pathological protein aggregates, including amyloid fibrils and prions, involved in neurodegenerative disorders. Here, we use computer simulations to identify the necessary requirements for the self-replication of fibrillar assemblies of proteins. We establish that a key physical determinant for this process is the affinity of proteins for the surfaces of fibrils. We find that self-replication can only take place in a very narrow regime of inter-protein interactions, implying a high level of sensitivity to system parameters and experimental conditions. We then compare our theoretical predictions with kinetic and biosensor measurements of fibrils formed from the Aβ peptide associated with Alzheimer’s disease. Our results show a quantitative connection between the kinetics of self-replication and the surface coverage of fibrils by monomeric proteins. These findings reveal the fundamental physical requirements for the formation of supra-molecular structures able to replicate themselves, and shed light on mechanisms in play in the proliferation of protein aggregates in nature.

The molecular machinery of life is largely generated through the assembly of proteins into functional complexes. A particularly common form of protein selfassembly is that leading to linear filaments. These structures are widely used in nature, for instance as the basis of the cytoskeleton. Once formed, the vast majority of functional protein assemblies typically fulfil their biological function but do not directly catalyse the formation of further “daughter” complexes. However, certain protein structures possess the intriguing ability to promote their own replication. This phenomenon first came to prominence in the context of prions, where specific supra-molecular protein assemblies were observed to be able to effectively multiply once taken up into a variety of organisms, ranging from humans to yeast [1–3]. Such propensity to self-replicate has emerged as a more general feature of pathological protein self-assembly, observed in the context of sickle cell anemia [4, 5] as well as for amyloid fibrils implicated in medical disorders [6–8], such as Alzheimer’s disease (Aβ peptide) [9, 10], type II diabetes (islet amyloid peptide, IAPP) [11–13], and Parkinson’s disease (α-synudein) [14, 15]. Strikingly, all of these structures are able to catalyse the formation of their own copies under certain conditions. The initial fibrils are produced spontaneously from solution through primary nucleation, followed by proliferation via heterogeneous, fibril-dependent, secondary nucleation [12]. In this type of self-replication the information about the protein conformation is transferred to the replicas, but they are not necessarily exactly identical to the parent aggregates. Spontaneous fibril formation is inherently slow, while fibril self-replication is usually many orders of magnitude faster [10]; yet a detailed microscopic understanding of either processes is currently lacking. Autocatalytic replication intrinsically introduces positive feedback into the self-assembly process that renders it challenging to control once assembly has started. As such, most functional protein complexes and fibrils do not have self-replicating properties. This finding therefore motivates the question about the fundamental ingredients necessary for fibril self-replication to occur, or indeed to be avoided.

Here, we develop a minimal computer model that is able to capture both spontaneous fibril formation in solution, and fibril-self replication. We study the necessary conditions required for self-replication to dominate over spontaneous formation, and find that strong bounds on inter-protein interactions exist for efficient self-replication that result in the high sensitivity of self-replication to environmental conditions. Indeed, it has been reported experimentally that the existence of secondary nucleation in α-synuclein, insulin, and Aβ peptide strongly depends on pH [14, 16, 17], while secondary nucleation in Aβ also varies dramatically with salt concentration [18]. The emergence of a narrow regime that supports self-replication sheds light on why it is relatively a rare property of protein self-assembly in vivo, and possibly provides a physical criterion to distinguish functional from pathological assembly. Moreover, these results suggest that even pathological self-assembly, in principle, can be suppressed by moderate changes to the system to move it from the narrow parameter space supporting self-replication. Our results further infer that the secondary nucleus has to be energetically different from the primary one, pointing to two distinctive pathways.

Taking the aggregation of the Alzheimer’s Aβ peptide into amyloid fibrils as a model for experimental comparison, in combination with kinetic and biosensing experiments, we show that the major characteristics of secondary nucleation can be explained by the adsorption of monomeric peptides onto the surface of fibrils, and the level of surface coverage. We then demonstrate, in simulations and in experiments, that self-replication can be modulated by controlling the fibril surface coverage. Through the powerful combination of coarse-grained simulations and physical measurements, our results offer microscopic insights into the mechanism of the autocatalytic replication of protein fibrils.

Computer model

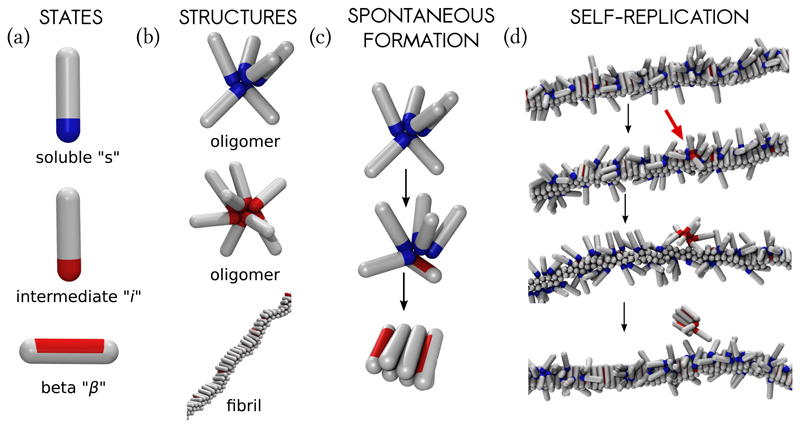
As the basis for our model we take the aggregation of peptides and proteins into amyloid fibrils, which have a common structure enriched in β-sheet content. A minimal model that reproduces homogeneous fibril nucleation allows an amyloidogenic protein to exist in two states: a soluble state (denoted “s”) that can form finite oligomers, and a higher free-energy state that can form the β-sheet enriched fibrils (denoted “β”) [19, 20]. Simply considering the interaction of soluble proteins with the surface of existing fibrils captures the binding of monomers to the fibrils, but does not lower the free energy barrier for nucleation, thus does not result in catalysis. To achieve a self-replication rate that is significantly faster than spontaneous formation, the structure and energy of the involved species necessarily have to differ from those observed in the absence of fibrils (Supplementary Section SI.C). The self-replication cycle in the Aβ system has been shown to predominately generate small prefibrillar oligomers, whose structures differ from that of the mature fibrils (Methods, [10, 21]). Although an ensemble of such intermediate structures could exist in reality, here we consider the simplest possible case: we include one additional, intermediate (“i”), conformation, which can take place on the fibril surface. This conformation is in-between the soluble and the β-state, and its selfinteraction is stronger than its interaction with the fibril, which leads to detachment of oligomers from the parent fibril, as observed in experiments.

Amyloidogenic protein in our model are represented as hard spherocylinders with attractive patches (Fig. 1). The attractive interactions account for generic features of inter-protein interactions, such as hydrophobic interactions, hydrogen bonding, and screened electrostatic interactions. The soluble state of the protein is modelled as a spherocylinder with an attractive tip (Fig. 1a), whose self-attraction is given by the parameter ϵ_ss. Such particles are able to make finite oligomers (Fig. 1b) [20]. The attractive tip can also adsorb onto the outer surface of the fibril, with interaction strength ϵ_sf (Supplementary Fig. S1). The intermediate conformation i is modelled with the same potential as the soluble state, but possesses a stronger self-association parameter ϵ_ii and a vanishing adsorption onto the fibril (Supplementary Fig. S1). The fibril forming, β-sheet prone, configuration is a hard spherocylinder with an attractive side-patch (Fig. 1a). The β-prone proteins pack parallel to one another with the maximal interaction strength ϵ_ββ, leading to fibril-like aggregates (Fig. 1b). We performed dynamic Monte Carlo (MC) simulations, allowing for the interconversion between the three protein conformations with a small probability at every MC step. The s → i → β conversion is thermodynamically unfavourable, reflecting the loss of the conformational entropy [22]. Further details are given in the Methods Section.

Fig. 1. The coarse-grained model and the nucleation processes in the system.

(a) The protein is allowed to exist in three conformations. From top to bottom: soluble state (“s”), intermediate conformation (“i”), and the β-sheet prone state (“β”), (b) Aggregated proteins. From top to bottom: oligomer made of soluble proteins, oligomer made of proteins in the intermediate state, and the fibril made of proteins in the β-sheet prone state, (c) Primary nucleation takes place in two steps. Soluble peptides form finite oligomers (top), which can convert into a nucleus of β-sheets (bottom), that continues growing, (d) Fibril self-replication (secondary nucleation). From top to bottom: Soluble protein monomers adsorb onto the surface of the preformed fibril, locally forming oligomers. Once peptides within an oligomer convert into the intermediate conformation (depicted with red attractive tips, accentuated with the red arrow), they become more prone to self-aggregation, which in turn leads to oligomer detachment. Finally, the detached oligomer converts into a nucleus of β-sheets, and continues growing. Snapshots were taken at ϵ_ss = 4kT, ϵ_sf = 8kT, and c = 50μM.

Spontaneous formation versus self-replication

The first question we address involves the identification of those conditions that lead to secondary nucleation being dramatically dominant over spontaneous, primary, nucleation. We have performed a series of computer experiments, in which a capped preformed fibril (incapable of further growth) was inserted into a solution of monomeric proteins, and nucleation processes were monitored. Primary nucleation takes place in two steps, whereby protein oligomers first form in solution, and then convert into β-sheet nuclei, which continue growing by monomer addition (Fig. 1c) [20, 23]. In the secondary nucleation process, proteins first adsorb onto the surface of the fibril, forming local clusters that keep growing and shrinking while still being attached to the fibril surface, as depicted in Fig. 1d. Once the oligomer of a critical size is formed, the proteins within change their conformation into the intermediate form. The oligomer then detaches into the solution, converts into the β-sheet protofibril, and grows further by monomer addition (Fig. 1d).

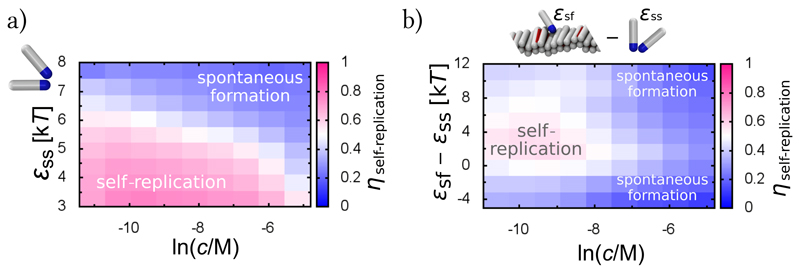
To investigate possible scenarios for different aggregating proteins, under various solution conditions, we measured the rates of primary and secondary nucleation at different protein concentrations and inter-protein interactions. From these measurements we calculated the fraction of self-replication events in the system for a given set of external conditions (Supplementary Sections SI.A and SI.B), Fig. 2a. Clearly, self-replication dominates over spontaneous fibril formation at low protein concentrations and low inter-protein interactions. Indeed, proteins are typically below their critical micelle concentration at physiological conditions, which corresponds to the regime of low inter-protein interactions and low protein concentrations, where self-replication can dominate.

Fig. 2. Conditions supporting fibril self-replication.

(a) The fraction of self-replication events, η_{self-replication}, in the total number of nucleation events, as a function of the peptide concentration c and the interaction between soluble peptides ϵ_ss. Peptide-fibril interaction is kept constant at ϵ_sf = 8kT. (b) Fraction of self-replication events as a function of the peptide concentration c and the difference between the peptide-fibril interaction and the peptide self-interaction (ϵ_sf − ϵ_ss), exhibiting a narrow regime where self-replication can be a dominant mechanism of formation. Data collected at ϵ_ss = 5kT.

The reason for the dramatic dominance of self-replication in this regime is two-fold. The first contribution arises from the aided collocation of proteins on the one-dimensional surface of the fibril. This contribution is particularly important at low protein concentrations, where the probability of proteins meeting in solution and forming oligomers is very low. The second contribution lies in the decreased barrier for the secondary nuclei formation on the fibril surface, via the intermediate state (Supplementary Section SI.C). Essentially, for self-replication to dominate, the secondary nucleus has to be different from the primary one.

Strong environmental bounds for self-replication

Modulating environmental conditions and introducing protein mutations not only changes the properties of proteins interacting in solution, but also the strength of the adsorption of proteins onto the surface of fibrils, given by ϵ_sf in our simulations. We find that changing the protein-fibril affinity only by a few kT, the fraction of self-replication events changes non-monotonically, exhibiting a distinct region of optimal self-replication, Fig. 2b. This result is in agreement with the high sensitivity of fibril self-replication to solution composition, and can explain why it is to date observed only in few systems. Comparably, in a recent simulation, secondary nucleation of Lennard-Jones particles at a crystalline surface, when exposed to mechanical agitation, was reported to take place only in the regime of intermediate supersaturation [24].

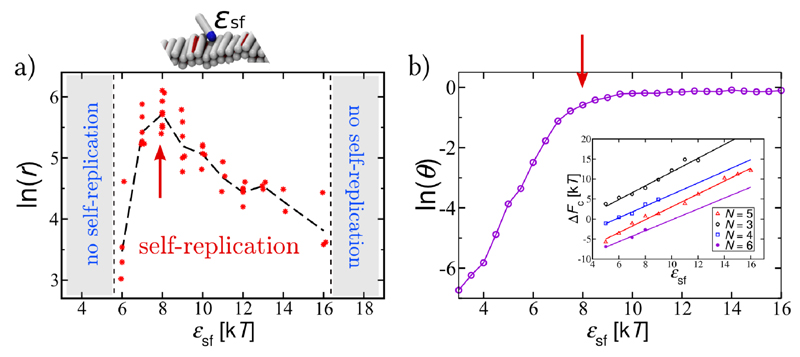
Fig. 3a. analyses this effect in depth, at constant protein concentration. At low protein-fibril interaction strengths, proteins cover only a small fraction of the fibril surface, and the protein adsorption and oligomer formation on the fibril surface determine the reaction rate. Fig. 3b depicts the Langmuir-type isotherm for the fibril surface coverage, θ, as a function of ϵ_sf (Supplementary Section SI.D), indicating that the increase in the surface coverage follows the increase in the rate of self-replication in Fig. 3a. At high ϵ_sf, the fibril is substantially covered by proteins, however, the oligomer detachment becomes unfavourable. Nucleation will happen only after the oligomer has reached a certain size, N*, when the energy gain due to the stronger inter-protein interactions after the conformational change overcomes the loss in the protein-fibril adsorption energy. Stronger binding to the surface hence requires larger oligomers in order to overcome the loss in the favourable adsorption energy. For very large oligomers, due to the geometric constraints, this requirement cannot be satisfied. Therefore, the conformational change will become unfavourable as the binding to the surface increases further (inset in Fig. 3b, Supplementary Section SI.E). In reality, in the regime of high adsorption, proteins are likely to distribute themselves evenly on fibrils in order to increase their contact area with the surface, and could form multiple layers, additionally hampering secondary nucleation. The narrow region of inter-protein interactions supporting self-replication is therefore the outcome of the balance between sufficient fibril coverage, and unhindered conformational change.

Fig. 3. Strong bounds for self-replication.

(a) Dependence of the rate of self-replication, r, on the peptide-fibril affinity, ϵ_sf. (b) Coverage of the surface of the preformed fibril (θ) as a function of ϵ_sf. Red arrows in (a) and (b) point to the area of the fastest self-replication, when the fibril is well covered with monomers. Inset: the free energy cost (ΔF_c) for the conversion of an oligomer of size N from the “s” conformation, that is attached onto the fibril, into the “i” conformation that detaches from the fibril surface. ΔF_c increases with the increase in the peptide-fibril affinity. All data are collected at ϵ_ss = 4kT and c = 0.15mM.

Kinetics of self-replication and comparison with experimental measurements

Our model makes a range of predictions that can be directly experimentally tested. Here, we seek to relate our simulations to kinetic measurements of self-replication of Aβ40 amyloid fibrils, one of the two major isoforms of the Aβ peptide associated with Alzheimer’s disease. Kinetic experiments usually determine the dependence of the reaction rate on monomer concentration, r ∼ c^γ, where the scaling exponent γ is the reaction order. It reflects the monomer dependence of the dominant aggregation processes, and is typically believed to be determined by the number of molecules reacting in the rate-limiting step, therefore carrying information about the reaction mechanism.

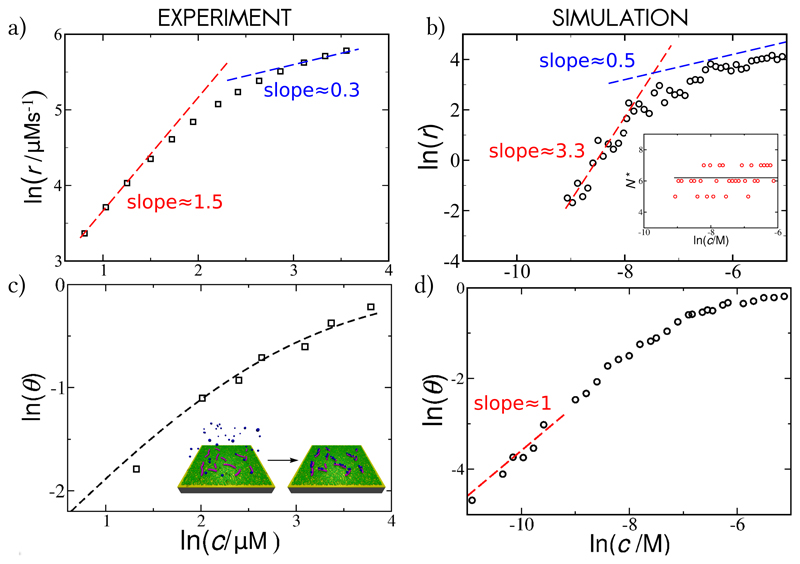
Fig. 4a depicts double logarithmic plot of the rate of secondary nucleation for the Aβ40 system, versus the initial monomer concentration, where the slope corresponds to the scaling exponent. Curiously, the scaling exponent is highly dependent on the concentration of the monomeric peptide in solution, suggesting a possible change in the nucleation mechanism over the concentration range [25]. Fig. 4b shows the same quantities, collected in simulations, at a moderate peptide-fibril affinity. The reaction order varies with the protein concentration, with a high value at low monomer concentrations (γ ≈ 3.3), and low value at high monomer concentrations (γ ≈ 0.5), as with the Aβ40 experimental data.

Fig. 4. Kinetics of fibril self-replication.

(a) Experimental results: The rate of secondary nucleation for the Aβ40 system versus the initial concentration of soluble monomers, from Ref. [25]. (b) Simulation results: The rate of secondary nucleation of fibrils with a moderate affinity for soluble monomers (ϵ_sf = 6kT) as a function of the concentration of the monomeric proteins in solution. Inset: the average critical oligomer size stays constant over the entire concentration range; the solid line plots the linear fit over the concentration range, (c) Experimental results: Fraction of the peptides bound to the surface of Aβ40 fibrils, θ, under the same conditions as the kinetic experiments in (a), versus the concentration of the monomers. The dashed line is the fit to the Langmuir isotherm with K⁻¹ = 15μM. Inset: schematic representation of the adsorption of monomeric peptides (coloured in blue) to the surface of fibrils (coloured in magenta), measured via SPR. (d) Simulation results: Surface coverage θ versus the concentration of free monomers at ϵ_sf = 6kT. Inter-peptide interaction is kept constant at ϵ_ss = 4kT for all simulation data.

Due to our microscopic modelling we are able to pinpoint the processes underlying the switch in kinetic behaviour. Fig. 4d shows that the change in the reaction order follows the trend in the change of fibril coverage. Hence, the non-linear increase in surface coverage, due to surface saturation, appears to be the cause of the continuous decrease in reaction order. It is beneficial to establish what controls the absolute value of the apparent reaction order (see Methods and Supplementary Section SI.F for details). We find that the rate of self-replication follows the surface saturation as ln(r) ∼ N*ln(Kc/(1 + Kc)), where K is the monomer-surface binding constant (K ∼ ϵ_sf) and N* is the size of the nucleating oligomer (found to be constant over the concentration range in our simulations, inset in Fig. 4b). The reaction order then continuously changes between γ → N*, at infinite dilution, and γ → 0 at full saturation. Since nucleation is possible within a finite time only when the surface coverage is non-negligible, observable values of γ will be necessarily smaller than N*.

Experimental verification of surface saturation

To test experimentally the prediction that the change in the apparent reaction order is governed by the change in the surface coverage, and not by a change in the nucleation mechanism, we designed a series of surface plasmon resonance (SPR) biosensing experiments that allow direct measurement of the binding of monomeric peptide molecules to the surface of amyloid fibrils, under the same conditions as the kinetic experiments. This enabled us to obtain the Langmuir absorption isotherm of Aβ40 peptides onto their own fibrils (Fig. 4c and Supplementary Fig. S6). Indeed, the surface saturation takes place in the micromolar regime (with an equilibrium binding constant of K⁻¹ = 15μM), which is exactly the regime where the change in the apparent reaction order takes place in aggregation experiments (Fig. 4a). Furthermore, this value of K is of the same order of magnitude as the value obtained from the kinetic fit to the experimental aggregation data (Methods and Supplementary Section SII), and therefore strongly supports the hypothesis that the change in exponent is due to surface saturation.

Surface saturation controls the apparent reaction order

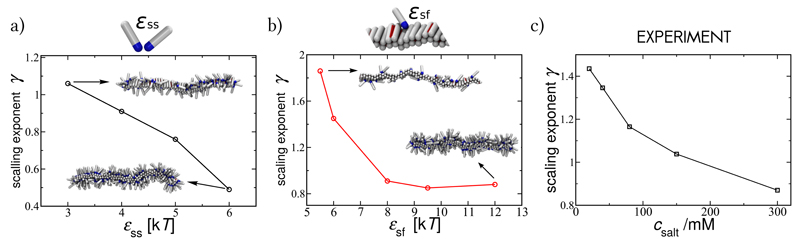
Finally, we show that by controlling the surface coverage via varying the strength of the inter-protein interactions, at constant monomer concentration, one can further modulate the kinetics of fibril self-replication. At constant protein concentration, the surface coverage is determined by the magnitude of protein-fibril affinity and inter-protein interactions. It is likely that both of these interaction strengths will be affected when altering experimental conditions, due to their similar physical origins. We observe that the surface coverage increases when both of these interactions are strengthened in simulations, resulting in a weaker dependence of self-replication on monomer concentration. The average scaling exponent γ from the simulations, as a function of ϵ_ss and ϵ_sf, is shown in Fig. 5a and Fig. 5b. We compare this behaviour to the aggregation of the Aβ42 at a range of NaCl salt concentrations [18], Fig. 5c. In the context of our physical model, two isoforms of Aβ peptide, Aβ40 and Aβ42, share mechanistic similarities. An increase in ionic strength shields the electrostatic interactions and leads to an increased attraction between the negatively charged Aβ42 monomers and fibrils, as well as the monomers to each other. Hence a variation of ionic strength offers an experimental way to vary in a controlled way the value of ϵ_ss and ϵ_sf. Indeed, the trend in the behaviour of the scaling exponents for the aggregation of Aβ42 with increasing salt concentration agrees well with that found in our simulations. Therefore the large effect of ionic strength on the aggregation behaviour is in agreement with a variation of the adsorption of peptides onto their fibrils, offering a direct way to influence the self-replication process in a controlled manner.

Fig. 5. The apparent reaction order is controlled by the surface saturation.

Simulation results: (a) Scaling exponent for the kinetics of fibril self-replication, averaged over the range of concentrations (20μM ≤ c ≤ 1mM), as a function of the interpeptide interaction between soluble monomers at constant peptide-fibril affinity ϵ_sf = 8kT, and (b) as a function of the peptide-fibril affinity at constant inter-peptide affinity ϵ_ss = 4kT. An increase in ϵ_ss and ϵ_sf increases the surface coverage, as shown by the representative snapshots in insets, taken at a monomer concentration c = 0.15mM. Experimental results: (c) The average scaling exponent for self-replication of Aβ42 fibrils at a range of NaCl concentrations, whose increase is expected to increase both ϵ_ss and ϵ_sf from Ref. [18].

Discussion and conclusions

By developing a minimal model of protein self-replication, we have identified its dominant physical determinant to be the adsorption of monomeric proteins onto the surface of protein fibrils. Strong limits on interprotein interactions are found for efficient self-replication, originating from the fact that changes in the interaction strength have opposing effects on the two parts of the nucleation mechanism: oligomer formation and oligomer detachment. A narrow region of “ideal” interaction values supporting self-replication (Fig. 2b) results in its high specificity and sensitivity to environmental conditions.

An additional conformational change taking place on the fibril surface is a minimal requirement for the catalysis and detachment of oligomers from the parent fibril, which, in the context of many amyloid diseases, is a crucial step in the proliferation of pathological species [26–28]. The conformational change is at the origin of the formation of amyloid fibrils; the aggregating protein necessarily undergoes a change from the soluble form into the characteristic β-hairpin conformation. Models which attempt to achieve self-replication in (nearly) minimal colloidal systems, require an external dynamical change to permit detachment of the replicas from the parents [29, 30]. Amyloidogenic proteins naturally possess this dynamic characteristic.

A direct practical contribution from our analysis is the ability to relate the reaction order measured in experiments to the underlying microscopic mechanism. We have found that the changes in the reaction order can be related to the change in the fibril surface coverage byproteins, which we have confirmed by directly measuring the binding isotherm of monomers to the fibril surface. The characteristic concentration-dependence of the reaction order, observed in experiments, is consistent with a scheme where the rate-limiting step takes place on the surface, further confirming that primary and secondary nucleation are indeed different processes. Whether the change in the apparent reaction order will be experimentally measured will depend on the concentration range that can be explored, as the experiments might be limited to a concentration range where it appears locally constant. By measuring the fibril coverage and the apparent kinetic reaction order separately, the information about the critical size of oligomers produced via secondary nucleation becomes directly accessible, for any protein system which exhibits this behaviour.

As a proof of principle, we have shown that by varying in a controlled manner the fibril surface coverage, by modulating the inter-protein interactions with ionic strength, one can control the kinetics of fibril self-replication. Hence the adsorption of monomeric proteins onto the surface of protein fibrils may pose a central target in limiting the proliferation of protein aggregates in a disease context.

Methods

The coarse-grained model and the choice of parameters

We use the model developed in Ref. [20], extended to capture secondary nucleation. In spirit, this model is similar to the multistate Potts model of Zhang and Muthukumar [31], and the recent model of Ilie, Otter and Brils [32]. Recently, more rigorous schemes have been developed to map coarse-grained inter-peptide interactions onto patchy-colloids for the purpose of studying protein aggregation by Ruff et al. [33, 34].

In our model each spherocylinder is σ = 2nm wide and L = 4σ = 8nm long. The hard core repulsion forbids for any distance between any two spherocylinders to be smaller than σ. The interaction between two peptides in the soluble “s” form is implemented as:

$$V_{ss}\left(r\right)=\{\begin{array}{ll}-{ϵ}_{ss}{\left(\frac{\sigma }{r}\right)}^6\hfill & \text{if}r\le 1.5\sigma \hfill \\ 0\hfill & \text{if}r>1.5\sigma \hfill \end{array}$$ (1)

where r is the distance between the centers of the attractive tips located at the spherocylinders’ ends. An attractive patch is added only at one spherocylinder pole to ensure formation of finite aggregates like those observed in experiments. This potential drives the formation of micellar-like oligomers, where tips of participating peptides are in contact in the oligomer center (Fig. 1B). The parameter ϵ_ss controls the strength of the non-specific interactions between the soluble peptides. Using atomistic simulations we estimated ϵ_ss to be relatively small, on the order of 5kT [20]. To explore the influence of different solution conditions, we varied it between 3kT and 8kT, as indicated in the text.

The interaction between two peptides in the intermediate conformation “i”, and between the soluble and the intermediate conformation is implemented using the same potential as in Eq. (1), with ϵ_ss → ϵ_ii and ϵ_ss → ϵ_si, respectively. The intermediate state is designed to be between the soluble and the β-sheet forming state, corresponding to a conformation with more β-content than the soluble state, but not yet a fully folded β-hairpin. Hence, the relative strength of interactions was always preserved, with ϵ_ss < ϵ_si < ϵ_ii. Their values were chosen such that nucleation is achieved within a reasonable computer time (see Supplementary Fig. S2), while preserving their relative strength; ϵ_ii is kept constant at ϵ_ii = 16kT, and ϵ_si is kept constant at ϵ_si = 8kT. Throughout the article k denotes the Boltzmann’s constant and T is the temperature.

The attractive side-patch of the β-sheet forming configuration is L_p = 0.6L long and spans an angle of 180°. If two patches face each other their interaction is:

$$V_{\beta \beta }\left(r\right)=\{\begin{array}{ll}-{ϵ}_{\beta \beta }{\mathit{\text{cos}}}^2\left(\varphi \right)-{ϵ}_{\beta \beta }\left(\frac{\sigma }{r}\right)\hfill & \text{if}d\le 1.5\sigma \hfill \\ 0\hfill & \text{if}d>1.5\sigma \hfill \end{array}$$ (2)

where ϕ is the angle between the axes of the particles, d is the shortest distance between the axes of the patches, and r is distance between the centers of the patches. The first term controls that peptides in the β-forms pack parallel to each other, mimicking the hydrogen-bond interactions between β-sheets, while the second term ensures compactness of the fibrils [22, 35, 36]. To drive the formation fo thermodynamically stable fibrils, ϵ_ββ has to be the strongest of all the interactions in the system. In this study we choose ϵ_ββ = 60kT [37, 38]. General aggregation of patchy-spherocylinders has been studied in details in our previous work [39].

The cross-interaction between the soluble and the β-sheet-forming configuration is designed as:

$$V_{s\beta }\left(d\right)=\{\begin{array}{ll}-{ϵ}_{s\beta }\hfill & \text{if}d<1.5\sigma \hfill \\ 0\hfill & \text{if}d>1.5\sigma \hfill \end{array}$$ (3)

where d is the shortest distance between the centre of the attractive tip and the axis of the β-patch, and ϵ_sβ = ϵ_ss + 1kT. The i-β interaction is described in the same way, with ϵ_sβ → ϵ_iβ, and ϵ_iβ = ϵ_ii + 1kT.

Peptide adsorption onto the preformed fibril is given by:

$$V_{sf}\left(d\right)=\{\begin{array}{ll}-{ϵ}_{sf}{\left(\frac{\sigma }{d}\right)}^6\hfill & \text{if}r\le 1.5\sigma \hfill \\ 0\hfill & \text{if}r>1.5\sigma \hfill \end{array}$$ (4)

where d is the shortest distance between the centre of the attractive tip of the soluble peptide and the body of the β-peptide (there is no other angular dependence). Adsorption of the intermediate “i” conformation onto the fibril is described in the same way (Eq. (4)), with ϵ_sf → ϵ_if, and ϵ_if = 1kT. The β-peptide interacts with the preformed fibril only via volume exclusion. The model parameters are summarized in Supplementary Figure S1.

MC Scheme

MC simulations were performed with small translational and rotational moves, to approach the realistic dynamics of the system. The interconversion between the three states was carried out with a small probability P = 0.0002, which mimics the slow conversion of the soluble peptide into fibril-forming β-sheet prone configuration. Every conversion from the soluble to the β-state is penalized with a change in the excess chemical potential of magnitude Δμ = 20kT, and the s → i and the i → β with 0.5Δμ (Fig. 1a). These values are chosen to reflect the fact that amyloidogenic proteins with small-to mid-β-propensity, such as Aβ, are typically not found in the β-sheet prone conformation in solution [40, 41].

Simulations were performed in a periodic cubic box in a grand-canonical ensemble, where the chemical potential of non-adsorbed soluble peptides was kept constant. This scheme was chosen to avoid the depletion of monomers from the solution due to the adsorption onto the surface of the preformed fibril. For this purpose, we do not distinguish between the monomeric soluble species, and the soluble species that are part of an oligomer in solution. The number of soluble peptides in the beginning of each simulation was set to ∼ 600, and the box size was adjusted to match the targeted peptide concentration. Soluble peptides are added or removed from anywhere in the simulation box, according to the grand-canonical scheme [42], excluding the r = 5σ region around the capped preformed fibril. All simulations were performed with the same size of the preformed fibril, which consists of N = 92 β-peptides and is unable to grow further. We were monitoring only the first generation of replicas, and have allowed the soluble peptides to adsorb only onto the preformed fibril, and not onto its replicas.

Kinetics of self-replication

In bulk experimental systems, the overall kinetics are determined by the processes of spontaneous nucleation in solution, elongation and self-replication, that all alter the fibril population. To compare bulk kinetic measurements to the modelling of nucleation on a single, growth-incompetent fibril used in simulations, it is necessary to dissect the macroscopic behaviour into its constituent processes. This can be achieved by developing a theoretical kinetic model and global fitting to the experimental kinetic data. We have adapted a theoretical kinetic model for the aggregation of Aβ40 [25] to include the Langmuir-like adsorption of peptides onto the growing fibril, and fit it to bulk experimental kinetic data to obtain the rate of secondary nucleation at various peptide concentrations. The details of the kinetic model as well as the global fits used to obtain this rate of secondary nucleation are shown in the Supplementary Section SII and Fig. S4.

Experimental exploration of intermediate oligomers in self-replication of Aβ42

If the oligomers generated through secondary nucleation were of the same structure as the fibrils, their concentration, [O], could be estimated from the known rate parameters for the fibrillar growth as $\left[O\right]=\frac{k_2{m}_{\text{tot}}^{n_2}}{2^{n_2}{+}^1{k}_{+}},$ where k₂ is the rate constant for secondary nucleation, k₊ is the fibril elongation rate constant and m_tot is the total protein concentration [43]. Using the values for the rate constants extracted from kinetic measurements of Aβ42 aggregation (k₂ ≈ 10⁴ M⁻²s⁻¹, k₊ ≈ 3 × 10⁶ M⁻¹s⁻¹ and m_tot = 5μM) [10], we find this concentration to be [O] ≈ 0.01 pM. This value is at least 5 orders of magnitude smaller than the experimentally measured concentration of oligomers in the same system (nanomolar range [10]), indicating that the structure of oligomers generated via such secondary pathway is necessarily different from that of the fibrils.

Scaling of the rate of self-replication with surface coverage

We recall that the conformational change, and subsequent fibril nucleation, is favourable only for oligomers above a certain critical size N*. The free energy of formation of such an oligomer on a finite surface scales as ΔF(N*) ∼ −N*ln(Kc/(1 + Kc)) where K is the monomer-surface binding constant (K ∼ ϵ_sf) and c is the free monomer concentration (Supplementary Section SI.G). Since the rate of the process depends exponentially on the negative magnitude of the free energy change for the critical oligomer formation, we obtain:

$$\text{ln}\left(r\right)\sim -\text{Δ}F\left(N^{*}\right)\sim N^{*}\text{ln}\left(Kc/\left(1+Kc\right)\right).$$ (5)

Supplementary Fig. S3 shows the free energy for oligomer formation on the fibril surface, ΔF(N), measured from the size-distribution of oligomers on the fibril in our simulations (Supplementary Section SI.F). As predicted, it decreases with increasing peptide concentration, reaching a plateau at high concentrations. An arrow in the Supplementary Fig. S3 marks the lowest concentration range at which we observe nucleation (−9 < ln(c) < −8). The slope at that point (≈ 0.6), multiplied by the average critical oligomer size (N* ≈ 6, inset in Fig. 4b), should give us the expected apparent reaction order in the kinetic plot γ ≈ 3.6. The measured reaction order at the same concentration range in Fig. 4b is γ ≈ 3.3, which agrees well with the predicted value within the error of our scaling theory and measurements.

SPR Experiments

Aβ40 amyloid fibrils were attached to the surface of an SPR biosensor and exposed to a solution containing monomeric Aβ40. In this case, monomers simulta neously attach both to the fibril ends and to their surfaces. However, due to their very different kinetics and thermodynamics, the two processes can readily be distinguished (Supplementary Section SIII). The elongation of fibrils will lead to a linear increase in mass, while the rate of attachment of peptide to the surface of fibrils is expected to decrease exponentially with time as the available binding sites become occupied. Conversely, upon washing the fibrils, the surface-bound peptide molecules are expected to show an exponential detachment behaviour, at high rates due to their relatively low binding free energy, while the rate of loss from the fibril ends by monomer dissociation is expected to be linear and very slow due to the high thermodynamic stability of the β-sheet rich fibrils [44]. By following the kinetic data of monomer detachment, we can distinguish the fast exponential from the slow linear dissociation (Supplementary Fig. S5), and obtain the amplitude of the exponential signal resulting from attachment to the surface of the fibrils, at various concentrations of the free monomers.