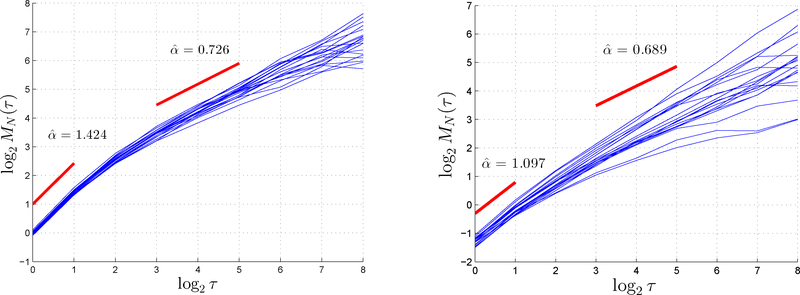
Figure 1: Bias and inconsistency over small scales τ vs vanishing bias and consistency as τ → ∞.

In general, taking the double limit τ,N → ∞ (see (8)) is necessary. Over fixed (“small”) lag values τ, TAMSD-based estimation is biased and, for most anomalous diffusion models other than fBm, inconsistent. As mathematically characterized by expansion (17), estimation bias is fundamentally a consequence of the fact that 〈log ·〉 ≠ log〈·〉 and of the presence of the small scale factor O(τ^−δ), whereas, in turn, inconsistency generally appears as a consequence of this same factor. The left and right plots show, respectively, 20 independent ifOU paths (length 2¹¹, α = 0.6) and 20 particle paths (length 1800) from P. aeruginosa biofilm after COS2-NO treatment at concentration level 8 mg ml⁻¹. The first and second red lines in each plot indicate, respectively, the fitted slope over small (τ = 1, 2) and large (τ = 8, 32) lag values. Based on the former lag values, A = 1.42 and 1.10 (evidence of superdiffusivity) for simulated and experimental data, respectively, whereas, by contrast, A = 0.70 and 0.69 (evidence of subdiffusivity) based on the latter. This illustrates the fact that bias and inconsistency vanish when τ (and N) becomes large.