Quintet-triplet mixing determines the fate of the multiexciton state produced by singlet fission in a terrylenediimide dimer at room temperature

Significance

Singlet fission is a process in which one of two adjacent organic molecules absorbs a single photon, resulting in rapid formation of one triplet state on each of the molecules. Theory predicts that if the two triplet states can separate and then generate two electron–hole pairs, the efficiency of a solar cell employing this material could rise from an upper limit of about 33 to 45%. Electron spin dynamics of the two triplet states can produce singlet, triplet, or quintet states having zero, two, or four unpaired electrons, respectively. We have discovered that triplet–quintet-state mixing at room temperature can open a pathway that annihilates triplet states, potentially diminishing the performance of solar cells using singlet fission.

Abstract

Singlet fission (SF) is a photophysical process in which one of two adjacent organic molecules absorbs a single photon, resulting in rapid formation of a correlated triplet pair (T₁T₁) state whose spin dynamics influence the successful generation of uncorrelated triplets (T₁). Femtosecond transient visible and near-infrared absorption spectroscopy of a linear terrylene-3,4:11,12-bis(dicarboximide) dimer (TDI₂), in which the two TDI molecules are directly linked at one of their imide positions, reveals ultrafast formation of the (T₁T₁) state. The spin dynamics of the (T₁T₁) state and the processes leading to uncoupled triplets (T₁) were studied at room temperature for TDI₂ aligned in 4-cyano-4′-pentylbiphenyl (5CB), a nematic liquid crystal. Time-resolved electron paramagnetic resonance spectroscopy shows that the (T₁T₁) state has mixed ⁵(T₁T₁) and ³(T₁T₁) character at room temperature. This mixing is magnetic field dependent, resulting in a maximum triplet yield at ∼200 mT. The accessibility of the ³(T₁T₁) state opens a pathway for triplet–triplet annihilation that produces a single uncorrelated T₁ state. The presence of the ⁵(T₁T₁) state at room temperature and its relationship with the ¹(T₁T₁) and ³(T₁T₁) states emphasize that understanding the relationship among different (T₁T₁) spin states is critical for ensuring high-yield T₁ formation from singlet fission.

Singlet fission (SF) is a spin-allowed photophysical process involving two organic molecules in which a photogenerated singlet exciton (S₁) can spontaneously down-convert to give two lower-energy triplet excitons (T₁) (1). SF is thought to occur via one of two general mechanisms: (i) direct coupling or (ii) mediation by charge-transfer (CT) states. In the former mechanism, SF occurs via a concerted two-electron process in which the initial S₁S₀ state is directly coupled to the correlated triplet pair ¹(T₁T₁) multiexciton state. The latter one involves a CT state that couples the S₁S₀ to the ¹(T₁T₁) state and occurs through two consecutive one-electron processes (1, 2). Interest in SF has risen because it offers the possibility to surpass the efficiency limit of single-junction solar cells beyond the Shockley–Queisser limit of 33% to nearly 45% (1, 3). Additionally, the (T₁T₁) states generated by SF are potential sources of four entangled spins for applications in quantum information science. Current studies on SF have focused on elucidating the mechanism and determining the nature of the intermediate electronic state with recent efforts focused on understanding the spin dynamics of the (T₁T₁) state and the processes leading to long-lived uncoupled triplet excitons (4–9).

Given that SF is inherently a multispin process, it is important to consider the spin quantum mechanics involved. The spin Hamiltonian of the (T₁T₁) state can be simply described by the sum of two single-particle Hamiltonians. Considering only the coupling of the spin angular momenta of the two triplets, nine eigenstates can be obtained from the Hamiltonian where one of the eigenstates is a singlet, three are triplets, and five are quintet states. Fine-structure interactions that couple these states lead to states with impure spin multiplicities, which results in mixing of the ¹(T₁T₁) and ⁵(T₁T₁) states. Application of an external magnetic field leads to redistribution of singlet character within the (T₁T₁) manifold, changing the number of eigenstates with singlet character. In the weak coupling regime, at zero field, three of the nine (T₁T₁) states have singlet character whereas at high fields, only two have singlet character (10). This redistribution of singlet character at different applied magnetic fields affects the relationship among the nine (T₁T₁) sublevels, making magnetic resonance techniques viable methods for understanding the (T₁T₁) state.

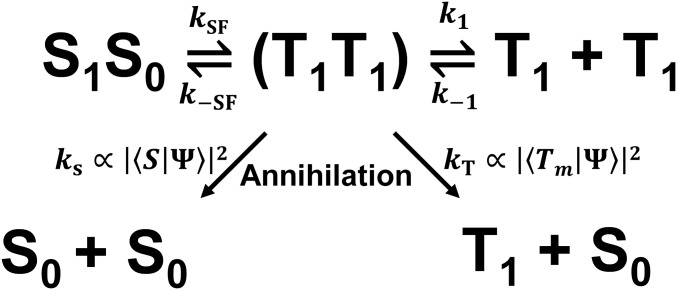
The precise spin character of the (T₁T₁) state greatly influences its evolution over time. The kinetic model shown in Fig. 1, which is adapted from the work of Merrifield et al. (10) on triplet fusion in organic crystals, describes the time evolution of the (T₁T₁) state. The triplets comprising the (T₁T₁) state can react in several ways: they can annihilate either through the singlet or triplet channels or can dissociate into two free triplets through diffusion or structural changes that lead to spin dephasing. If the energetics are satisfied [E(S₁) ∼ 2E(T₁)], the triplets can also annihilate to form S₀ + S₁, which can be detected by delayed fluorescence. The fraction of the (T₁T₁) population that can annihilate through a specific channel is proportional to the amount of singlet or triplet character in the (T₁T₁) wavefunction. These annihilation pathways are especially relevant in covalent dimers for which dissociation into two free triplets is limited by their restriction to two interacting sites, unlike in molecular crystals. Recent studies on polyacenes have shown that the ¹(T₁T₁) state produced initially via SF can acquire quintet, ⁵(T₁T₁), character before spin decoherence occurs, leading to two noninteracting triplet states or mutual annihilation (4–9). Most studies on SF quintets are conducted at low temperatures due to rapid dephasing and challenges associated with observing these states in solution. However, recently, SF quintets have been observed in dilute pentacene films at room temperature. Although quintet formation has been observed in polyacene systems, the decay mechanism of the different SF-generated (T₁T₁) spin states, especially the ³(T₁T₁) state, has not been well studied. Understanding these decay mechanisms is essential as they play a significant role in determining the overall T₁ yield derived from SF.

Fig. 1.

Kinetic model describing the time evolution of the (T₁T₁) state. <S| is the singlet ¹(T₁T₁) state vector, <T_m| are the three ³(T₁T₁) state vectors, and |Ψ> is the total spin wavefunction. The relative yields of the two annihilation pathways are determined by the singlet and triplet character of the wavefunction |Ψ>. k_SF, k_-SF, k₁, and k_-1 correspond to singlet fission, (T₁T₁) geminate fusion to S₁ + S₀, triplet dissociation, and bimolecular triplet–triplet fusion, respectively.

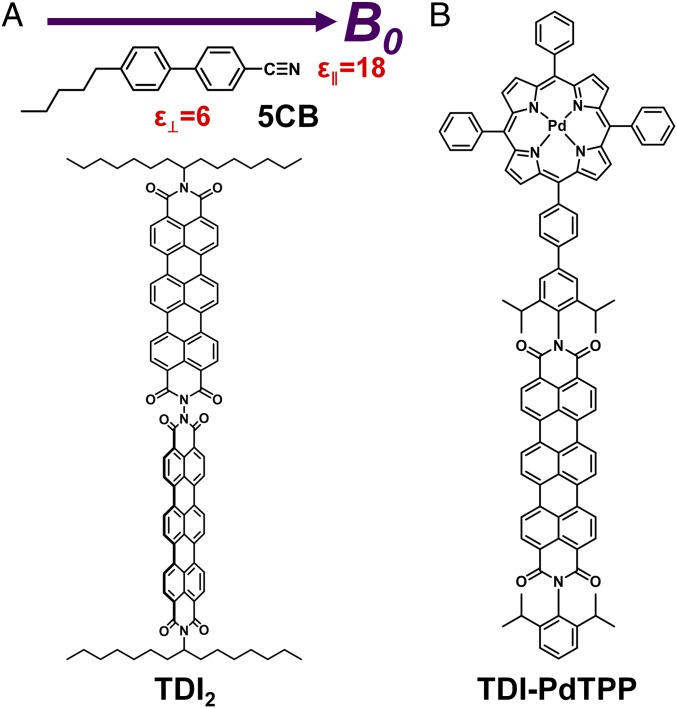
In this article, we discuss the spin evolution of the (T₁T₁) state in a covalently linked terrylene-3,4:11,12-bis(dicarboximide) (TDI) dimer (TDI₂) in which the two TDI molecules are attached directly at their imide positions (Fig. 2). TDI fulfills the energetic requirement for exoergic SF [E(S₁) = 1.83 eV and E(T₁) ≤ 0.77 eV] (11) and has been a target of SF studies due to its high stability, easy synthetic modification, and strong visible absorption (12). Previously, SF has been observed in TDI covalent dimers (11, 12) and films (13). Attachment at the imide position provides sufficient electronic coupling for SF to kinetically outcompete other excited-state processes; however, the orbital nodes at the imide positions lead to small enough coupling between the TDI units such that spin evolution of the (T₁T₁) state can occur before dephasing, ultimately resulting in long-lived triplets. Here, we investigate the (T₁T₁) dynamics of TDI₂ in 4-cyano-4′-pentylbiphenyl (5CB), a room-temperature nematic liquid crystal, which was chosen as the solvent because (i) application of a magnetic field aligns the 5CB director along the field, which, in turn, aligns the dimer relative to the field, and (ii) the viscosity of 5CB inhibits significant dimer motion, which is necessary to observe quintet and triplet states by time-resolved electron paramagnetic resonance (TREPR) spectroscopy. Using complementary transient visible and near-IR absorption and TREPR spectroscopies, we observe the formation of the ⁵(T₁T₁) state, its spin evolution, and subsequent triplet-pair annihilation through the triplet channel to uncorrelated triplets (Fig. 1). The uncorrelated triplet yield is magnetic field dependent, with a maximum triplet yield at ∼200 mT due to mixing of the ⁵(T₁T₁) and ³(T₁T₁) states.

Fig. 2.

(A) Structure and orientation of TDI₂ relative to the magnetic field (B₀) and the director (L) of 5CB and (B) structure of the TDI-PdTPP dyad.

Results and Discussion

Synthesis and Steady-State Characterization.

TDI₂ was synthesized via stepwise condensation of 4-bromo-1,8-naphthalic anhydride and hydrazine, followed by two Suzuki couplings with N-(8-pentadecyl)-9-(4,4,5,5-tetramethyl-1,3,2-dioxaborolan-2-yl)-perylene-3,4-dicarboximide and ring-closing of the terrylene cores under basic conditions (SI Appendix, Fig. S2A). In the absorption spectra of TDI₂, the relative intensities of the 0–0 and 0–1 vibronic bands centered at 672 and 615 nm, respectively, are similar to that of monomeric TDI (SI Appendix, Fig. S3A). The similar vibronic structure suggests that electronic coupling between the two TDI subunits is relatively weak, which is expected since the nodes of the TDI frontier orbitals bisect the two nitrogen atoms at the imide positions. According to density functional theory (DFT) calculations, the two TDI subunits of the dimer are positioned perpendicular to one another, which improves its solubility (SI Appendix, Table S3). We also synthesized a covalently linked TDI-palladium meso-tetraphenylporphyrin dyad (TDI-PdTPP) in which PdTPP acts as a triplet sensitizer to generate ^3*TDI as a spectroscopic standard. The dyad was synthesized by coupling N-(4-bromo-2,6-diisopropylphenyl)-N′-(2,6-diisopropylphenyl)-terrylene-3,4:11,12-tetracarboxdiimide to 5,10,15-triphenyl-20-[4-(4,4,5,5-tetramethyl-[1,3,2]dioxaborolan-2-yl)-phenyl]-porphyrin, followed by metallation with PdCl₂ (SI Appendix, Fig. S2B). Palladium was chosen as the metal center to promote heavy-atom–induced spin-orbit intersystem crossing (ISC). The absorption spectrum of TDI-PdTPP exhibits a Soret band centered at 418 nm, Q bands at 524 and 555 nm, and TDI shows 0–0 and 0–1 vibronic bands at 653 and 600 nm, respectively (SI Appendix, Fig. S3B).

Femtosecond Transient Absorption Spectroscopy.

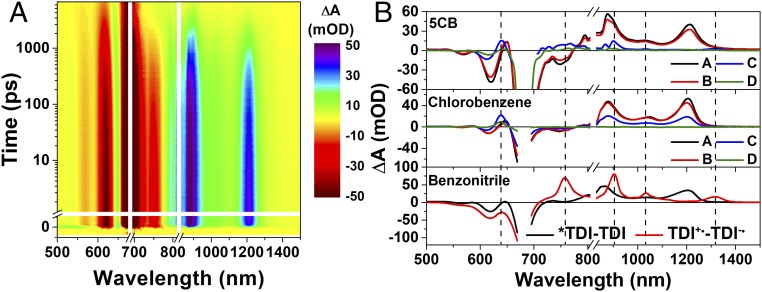
Femtosecond transient absorption (fsTA) spectra of TDI₂ were collected in 5CB in a static magnetic field B₀ = 345 mT to align the liquid crystal director $\overrightarrow{\mathit{L}}$ along $\overrightarrow{\mathit{B}}$ matching the conditions employed for the TREPR measurements (Fig. 3). Upon photoexcitation of TDI₂ at 685 nm, we observe strong ground-state bleach (GSB) features at 620 and 682 nm, stimulated emission (SE) at 748 nm, and S_n ← S₁ excited-state absorption (ESA) features at 876, 1,031, and 1,211 nm, along with a feature with a maximum at 649 nm (SI Appendix, Fig. S4). Based on our earlier work (11), the 649-nm feature is assigned to the T_n ← T₁ ESA of the (T₁T₁) state. Immediate formation of this feature suggests that SF occurs within the ∼200-fs instrument response function (IRF) of the experiment. The decay of the S_n ← S₁ near-infrared (NIR) bands and SE is also accompanied by growth of a much lower amplitude set of features at 767, 900, 1,031, 1,201, and 1,308 nm. The feature at 767 nm results from TDI^+•, while the other four features are assigned to TDI^−• (11). There is also an apparent blue-shift of the feature at 649 to 642 nm over the course of ∼8 ns. Similar dynamics are observed at B₀ = 0 mT (SI Appendix, Fig. S5).

Fig. 3.

(A) Contour plot of the fsTA data of TDI₂ in 5CB collected at 345 mT, λ_ex = 685 nm. Data near 685 and 820 nm are omitted due to pump scatter and residual light used to generate the white-light probe pulse, respectively. (B) Evolution-associated spectra of TDI₂ in 5CB (345 mT), chlorobenzene (345 mT), and benzonitrile (0 mT). The dashed vertical lines in the spectra are located at prominent triplet, TDI^+•, and TDI^-• features.

Evolution-associated spectra (EAS) were generated by fitting the dataset to a sequential four-state (A → B → C → D) model. The EAS of state A include features belonging to both the singlet and (T₁T₁) states. We assign state A to a mixed state that has both S₁S₀ and ¹(T₁T₁) character; such mixed multiexciton character has been observed in other TDI dimers and is a result of weak vibronic coupling (14). We assign singlet-spin character to the (T₁T₁) state A because the initial (T₁T₁) state needs to have an overall singlet spin to allow for SF. The EAS of state B is similar to that of state A; however, the ratio of the NIR singlet and visible (T₁T₁) features changes, suggesting that the composition of the mixed state evolves over time. State B decays at k = (1.8 ± 0.1 ns)⁻¹ to form a small amount of state C, which has observable TDI^+• and TDI^−• features in the NIR region. State C eventually decays at k = (3.0 ± 0.4 ns)⁻¹ to form state D, which has little or no CT character and lives beyond the 8-ns window of this experiment. This model does not include the k_SF component discussed in Fig. 1 because SF occurs within the ∼200-fs IRF. Thus, this four-state model only monitors the electronic character of the (T₁T₁) multiexciton state; the different states have different contributions of S₁S₀ and (T₁T₁) character with state D having exclusively (T₁T₁) character.

The observed dynamics can be explained by considering the anisotropic dielectric constant of aligned 5CB (ε_⊥ = 6 and ε_‖ = 18). The dimer’s behavior in aligned 5CB is most similar to that in nonpolar chlorobenzene (ε_‖ = 5.6), suggesting that TDI₂ is primarily aligned along the short axis of the liquid crystal. In chlorobenzene, TDI₂ forms a mixed state with both S₁S₀ and ¹(T₁T₁) character immediately upon photoexcitation and the states evolve similarly to those observed in 5CB (SI Appendix, Figs. S6 and S7). Notably, in both 5CB and chlorobenzene, we observe a blue-shift of the maximum of the triplet feature from ∼649 to 640 nm over the 8-ns experimental window. We assign this shift to the evolution of the ¹(T₁T₁) state, which is discussed in detail below.

Observation of the low-amplitude but sharp features characteristic of TDI^+• and TDI^−• features in 5CB suggests that some of the TDI₂ may be undergoing symmetry-breaking charge separation (SB-CS). These features were not observed in chlorobenzene, which suggests an environmental influence specific to 5CB. The size of the aligned 5CB domains varies depending on the strength of the applied magnetic field (15–17). At B₀ = 345 mT, a small fraction of 5CB remains unaligned, which generates, on average, a more polar environment than that of the aligned domains. For comparison, in benzonitrile (ε = 26, comparable to ε of 5CB), TDI₂ undergoes SB-CS [k_CS = (84 ± 5 ps)⁻¹] and recombination to the ground state [k_CR = (449 ± 6 ps)⁻¹] with no evidence of triplet formation (SI Appendix, Fig. S8).

The room-temperature nanosecond transient absorption (nsTA) spectra of TDI₂ obtained at B₀ = 345 mT in aligned 5CB are shown in Fig. 4A. The formation of the (T₁T₁) state occurs within the IRF, as indicated by the fsTA data. The triplet ESA spectrum decays biexponentially with rate constants of (18 ± 5 ns)⁻¹ and (93 ± 9 μs)⁻¹; the initial decay is also accompanied by a spectral shift. Similar dynamics are observed at B₀ = 0 mT (SI Appendix, Fig. S9).

Fig. 4.

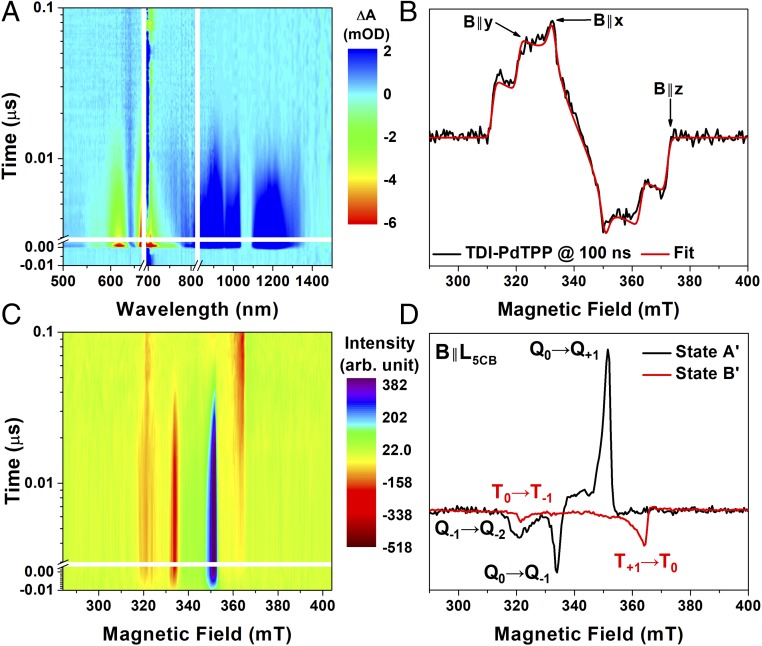
(A) Contour plot of the nsTA data of TDI₂ in 5CB collected at 345 mT, λ_ex = 685 nm. Data near 685 nm are omitted due to pump scatter. (B) TDI triplet-state EPR spectrum of TDI-PdTPP in butyronitrile at 105 K, λ_ex = 660 nm. (C) Contour plot of the TREPR spectra (X band) of TDI₂ in 5CB collected at room temperature, λ_ex = 660 nm, and (D) its corresponding EAS obtained using procedures discussed in the text. The dominant absorptive and emissive transitions have been assigned where Q_m and T_m refer to the ⁵(T₁T₁), m_s = m and T₁, m_s = m sublevels, respectively.

Assigning the TDI Triplet Electron Paramagnetic Resonance Spectrum.

Knowledge of the expected zero-field splitting (ZFS) parameters, D and E/D, for TDI is necessary for proper assignment of the spectral features in the electron paramagnetic resonance (EPR) spectrum following singlet fission in TDI₂. To determine these values, we synthesized a dyad, TDI-PdTPP, in which PdTPP is used to sensitize the formation of ^3*TDI, which was confirmed by transient absorption spectroscopy (SI Appendix, Fig. S10). Photoexcitation of TDI-PdTPP in toluene at 655 nm results in TDI GSB features at 600 and 658 nm, TDI NIR S_n ← S₁ ESA at 893, 1,066, and 1,225 nm, and SE at 733 nm. The TDI singlet undergoes rapid energy transfer to PdTPP to form ^1*PdTPP followed by heavy-atom–induced spin-orbit ISC to give ^3*PdTPP, and subsequent energy transfer back to TDI to yield ^3*TDI. Formation of ^3*TDI is corroborated by the appearance of a feature at ∼618 nm that corresponds to the T_n ← T₁ transition of ^3*TDI. In the nsTA data, all of the singlet ESA features eventually disappear, leaving only long-lived TDI triplet after ∼20 ns. The EPR spectrum of TDI-PdTPP (butyronitrile, 105 K) at 100 ns following photoexcitation at 660 nm and its corresponding fit are shown in Fig. 4B. The triplet EPR spectrum was fit with ZFS parameters, |D| = 848 MHz and E/D = 0.133, and the a-a-a-e-e-e spin-polarization pattern (where a = enhanced absorption and e = emission, low to high magnetic field) was generated as a result of preferential population of the $|{\text{T}}_{\text{z}}\rangle$ zero-field spin state (SI Appendix, Fig. S11 and Table S1) (18).

Spin Evolution of the (T₁T₁) State.

The TREPR spectra of TDI₂ (Fig. 4C) provide information about the spin character of the (T₁T₁) state as it decays. The TDI₂ TREPR spectra were fit with an A′ → B′ → ground model to generate the EAS shown in Fig. 4D (SI Appendix, Fig. S12). Formation of the (T₁T₁) state (state A′) occurs within the 17-ns IRF and decays to a T₁ lineshape (state B′) at k = (21 ns)⁻¹; this is consistent with the initial triplet decay rate observed in the nsTA data [(18 ± 5 ns)⁻¹]. The T₁ state decays at k = (890 ns)⁻¹, which is the lower limit for the T₁-state lifetime due to the absence of explicit spin relaxation in the evolution-associated model. The (T₁T₁) EPR spectrum is composed of three dominant transitions: emissive and absorptive peaks at 334 and 351 mT, which originate from the m_s = 0 level of the ⁵(T₁T₁) state, and a broad emissive feature at 320 mT that arises from the m_s = −1 level of the ⁵(T₁T₁) state (Fig. 4D). The fully emissive EAS of state B′ was fit as a spin-polarized triplet with |D| = 861 MHz and E/D = 0.133 where the high-field eigenstates are spin polarized with preferential population of the T₊₁ state followed by the T₀ state. The unusual spin polarization of the triplet T₊₁ state is likely due to enhanced mixing between the ³(T₁T₁), m_s = +1 and the ⁵(T₁T₁), m_s = −1 eigenstates (vide infra). In agreement with the fsTA, the triplet spectrum shows partial ordering with alignment of the short molecular axis along the director of 5CB. The EAS of state A′ was fit with the following coupled triplet-pair spin Hamiltonian (4, 19):

$$\widehat{\mathbf{\mathscr{H}}}={\displaystyle \sum _{\mathit{i}=\mathit{a},\mathit{b}}}\left(g{\mu }_B\mathit{B}\cdot {\widehat{\mathit{S}}}_i+{\widehat{\mathit{S}}}_i\cdot \mathit{D}\cdot {\widehat{\mathit{S}}}_i\right)+\mathit{J}{\widehat{\mathit{S}}}_{\mathit{a}}\cdot {\widehat{\mathit{S}}}_{\mathit{b}}\mathrm{,}$$ [1]

where ${\mu }_B$ is the Bohr magneton; B is the magnetic field vector; g is the electron g value; D is the ZFS tensor; J the triplet–triplet interaction tensor where J > 0 results in E(⁵(T₁T₁)) > E(³(T₁T₁)) > E(¹(T₁T₁)); and S_i are the spin operators of the individual triplets. Unlike in the original Merrifield model (10), we include J in our analysis because its magnitude and sign strongly influence the level-crossing mechanism (20). The ZFS tensor was fixed to the value obtained from fitting state B′, |D| = 861 MHz and E/D = 0.133, which is comparable to the ZFS parameters obtained for TDI-PdTPP. The fit was performed using a method similar to that described in Tayebjee et al. (4) (SI Appendix, Table S2). Briefly, the intensity of each transition is proportional to the degree of singlet character in each numerically calculated eigenstate.

Formation of T₁ from the (T₁T₁) state is corroborated by the nsTA spectra collected in chlorobenzene in which the (T₁T₁) and T₁ spectra are distinguishable. According to the EAS (SI Appendix, Figs. S13 and S14), which were generated by fitting to a sequential four-state (A″ → B″ → C″ → D″ → ground) model, the decay of the (T₁T₁) state (state C″) is accompanied by a 9-nm blue-shift to 628 nm of the triplet ESA and the growth of a shoulder at 652 nm. The final EAS (state D″) matches the anthracene-sensitized triplet spectra of TDI₂ in chlorobenzene (SI Appendix, Fig. S15) and thus confirms T₁ formation.

The dynamics observed in TDI₂ by TREPR and nsTA can be explained by the decay pathways of the (T₁T₁) state described in Fig. 1. The initial singlet character of the (T₁T₁) state generated by SF allows for population of not only ¹(T₁T₁), but also the ⁵(T₁T₁), m_s = 0 and ⁵(T₁T₁), m_s = −1 sublevels, which leads to the following pathways: (i) A majority of the (T₁T₁) state population has singlet character that decays nonradiatively through annihilation via the singlet channel to the ground state (k_S); (ii) Some of the (T₁T₁) population competitively annihilates through the triplet channel (k_T), which results in a single long-lived triplet on TDI₂. We observe competitive annihilation because some of the (T₁T₁) population develops both ³(T₁T₁) and ⁵(T₁T₁) character. Annihilation from the ³(T₁T₁), m_s = +1 state results in preferential population of the T₊₁ state due to conservation of angular momentum, thus explaining the completely emissive triplet spectrum; (iii) Lastly, a small population of the (T₁T₁) state dissociates to form two free triplets (k₁), accounting for some of the long-lived triplet observed in TDI₂. This dissociation occurs through small changes in geometry, which is possible in a room-temperature liquid crystal environment. We do not consider geminate fusion to S₀ + S₁ (k_−SF) in this system since this process is endoergic and not thermally accessible due to the ∼0.3-eV difference between E(S₁) and 2E(T₁) in TDI, unlike in less endoergic systems such as tetracene (21), rubrene (22), and 1,6-diphenyl-1,3,5-hexatriene (23) in which triplet fusion is observed through delayed fluorescence. The lack of delayed fluorescence is corroborated by time-resolved fluorescence (TRF) spectroscopy on TDI₂ (SI Appendix, Fig. S16). The plateau at zero by the end of the 20-ns experimental window in the TRF kinetics is consistent with the SE and singlet ESA features in the fsTA. We also rule out annihilation of the (T₁T₁) state to yield the Q₁ + S₀ state because this process is strongly endoergic according to DFT calculations in which the energy of the quintet state localized on a single chromophore is 3.87 eV, which is ∼2 eV greater than the S₁ energy (SI Appendix, Fig. S20 and Table S4).

Magnetic-Field Effects on the Triplet Yield.

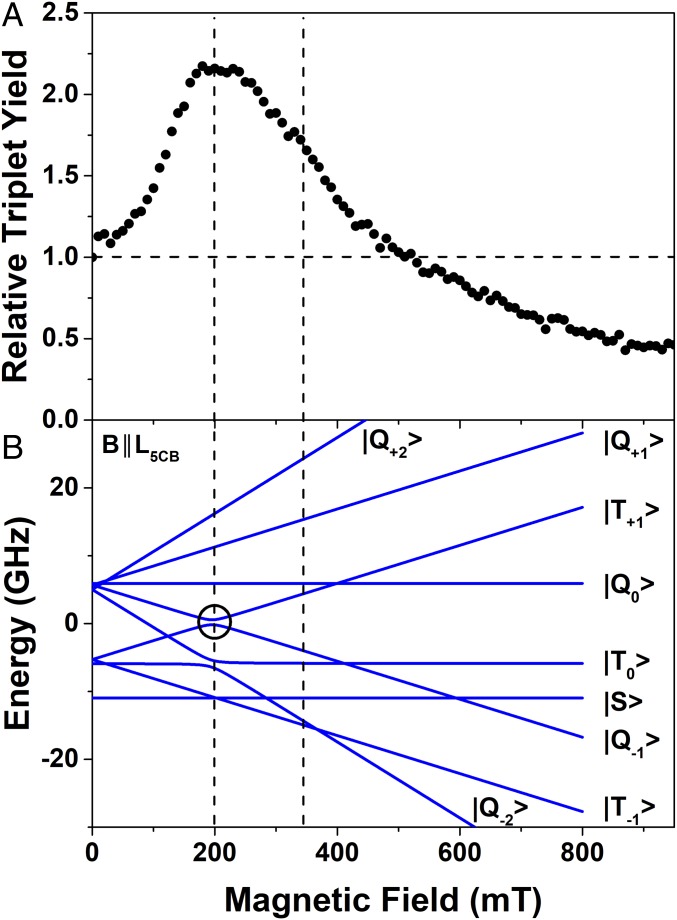
Previous studies on SF chromophores have observed magnetic-field effects (MFEs) on both fluorescence (20–22, 24–27) and device performance (28). The shape of the MFE curve depends on the level-crossing mechanism of the (T₁T₁) pairs and thus provides valuable information on how to tune the mixing of the various (T₁T₁) states. MFE studies on fluorescence often rely on the presence of geminate fusion of (T₁T₁) pairs to S₀ + S₁ as it influences both the delayed fluorescence kinetics and the steady-state fluorescence spectra. Since geminate fusion of the (T₁T₁) pair is not energetically favorable in TDI₂, we gained further insight into the evolution of the (T₁T₁) state by monitoring the terminal triplet yield as a function of magnetic field. Fig. 5A shows the triplet yield, normalized to the yield at 0 mT, of TDI₂ in chlorobenzene at room temperature at 2 μs following photoexcitation. With increasing magnetic field, the triplet yield nearly doubles, reaching a maximum at 200 mT, which is followed by a decrease and eventual plateau at a decreased yield as the field approaches 1 T. This maximum is consistent with the small J = 5.33 GHz (190 mT) of TDI₂, which was obtained from fitting the TREPR data. As shown in Fig. 5B, the 200-mT maximum coincides with the avoided crossing between the ³(T₁T₁), m_s = +1 and ⁵(T₁T₁), m_s = −1 and the ³(T₁T₁), m_s = 0 and ⁵(T₁T₁), m_s = −2 levels. The (T₁T₁) state achieves the maximum amount of ³(T₁T₁) character at the former avoided crossing because the ⁵(T₁T₁), m_s = −1 sublevel is populated upon SF, thereby maximizing the triplet yield through annihilation via the triplet channel. These results were corroborated by high-field TREPR measurements at Q band (33.6 GHz), where the ⁵(T₁T₁), m_s = −1 state no longer mixes with the ¹(T₁T₁) and is therefore no longer populated, resulting in the loss of the ⁵(T₁T₁), m_s = −1 → ⁵(T₁T₁), m_s = −2 transition in the TREPR spectrum (SI Appendix, Fig. S17). The triplet yield was below our detection threshold, which suggests that the ⁵(T₁T₁), m_s = −1 sublevel plays a major role in triplet formation.

Fig. 5.

(A) Triplet yield relative to that at 0 mT of TDI₂ in chlorobenzene as a function of magnetic field. Spectra were averaged from 620 to 640 nm and integrated from 2 to 20 μs. (B) Energy level diagram depicting the relationship of the singlet (|S>), triplet (|T>), and quintet (|Q>) spin states of (T₁T₁) as a function of magnetic field; the diagram was generated for TDI₂ oriented in 5CB. The dashed vertical lines are located at 200 and 345 mT. The avoided crossing between the ³(T₁T₁), m_s = +1 and ⁵(T₁T₁), m_s = −1 levels (see circled region) results in maximum ³(T₁T₁) character in TDI₂.

The boost in triplet yield is not due to increased (T₁T₁) formation because there are no significant differences in the early time dynamics of TDI₂ at 0 and 345 mT (SI Appendix, Figs. S6 and S7). We also monitored the MFE on the rate of (T₁T₁) decay, which is an effective rate (k_eff = k_S + k_T + k₁) that accounts for singlet-channel annihilation (k_S), triplet-channel annihilation (k_T), and dissociation (k₁) (SI Appendix, Fig. S18). k_eff is minimized when the triplet character of the (T₁T₁) state is maximized and consequently the singlet character is minimized. There is an observable effect because k_S becomes smaller relative to k_T and k₁ because k_S is proportional to the amount of singlet character in the wavefunction. Lastly, we monitored the MFE on the singlet character using the SE and ESA features (SI Appendix, Fig. S19). These MFEs have similar shapes to that of the triplet yield because of the inverse relationship between singlet and triplet character but the relative effect is minor (<10%) compared with that on the triplet yield. There is also no significant change in the respective decay kinetics as a function of magnetic field.

We can approximate the branching ratios between dissociation from the (T₁T₁) state and competitive annihilation via the triplet channel from the MFE on triplet yield. At zero field, almost all triplet formation can be accounted for by triplet dissociation because there is little ³(T₁T₁)–⁵(T₁T₁) mixing, resulting in branching ratios of 100 and 0%, respectively. If the additional triplet yield observed is due to annihilation through the triplet channel, then the resulting branching ratios at 200 mT are ∼23 and ∼77%, respectively. This magnetic field dependence suggests that weak magnetic fields applied to future devices that utilize SF triplets may be able to tune their performance.

We observe the ⁵(T₁T₁) state of TDI₂ at room temperature because the viscosity of 5CB aligned by the magnetic field limits averaging of the anisotropic magnetic interactions that is typical in isotropic liquid solvents. Mixing of the ³(T₁T₁) and ⁵(T₁T₁) states has not been observed in previous SF dimers that form quintets. The small J value of TDI₂, compared with that of pentacene dimers (20–30 GHz), allows for observation of this mixing at conventional EPR magnetic fields. The magnitude of J is small due to the weak wavefunction overlap dictated by the nodal structure of rylenediimides (29), in which both the highest occupied molecular orbital and lowest unoccupied molecular orbital have nodal planes that bisect their two nitrogen atoms. The spin mixing in TDI₂ allows (T₁T₁) annihilation through the triplet channel (k_T) to become a competitive pathway for independent triplet formation that is not available to systems with larger J values. Thus, when designing SF dimers, one should consider the magnitude of J for the system as it influences the availability of competing pathways.

Although (T₁T₁) annihilation pathways have been a concern for covalent dimers and oligomers undergoing SF (30), the triplet channel for (T₁T₁) annihilation is also relevant to noncovalent SF systems. In the solid state, free triplets generated by SF can undergo triplet fusion to reform the (T₁T₁) state with a one-in-three probability of having an overall triplet spin. Thus, one-third of the triplets that undergo triplet fusion can potentially annihilate through the triplet channel, diminishing the overall T₁ yield. This loss channel has serious consequences for future SF devices, which will rely on high triplet yields to enhance efficiencies. The triplet-channel annihilation pathway is also important to consider in up-conversion systems that depend on efficient triplet–triplet annihilation to excited-state singlets. Similar to potential SF devices, annihilation through the triplet channel is an undesired pathway as it diminishes the total amount of triplets that can annihilate to form the targeted excited-state singlets.

Conclusions

A weakly coupled TDI dimer is shown to undergo ultrafast SF to generate (T₁T₁) states with mixed electronic and spin character. The rigidity of TDI₂ combined with its alignment in the nematic liquid crystal 5CB allows for observation of the ⁵(T₁T₁) state at room temperature. The ⁵(T₁T₁) and ³(T₁T₁) states of TDI₂ mix, resulting in competitive annihilation via the triplet channel to form long-lived uncorrelated triplets. The mixing and thus triplet-channel annihilation is magnetic field dependent, emphasizing the importance of the (T₁T₁)-state spin multiplicity. Thus, formation of a pure ⁵(T₁T₁) state is essential to producing a high yield of a pair of uncorrelated triplets because it affords protection from both singlet- and triplet-channel annihilation pathways. Overall, we demonstrate that the spin dynamics among the ^1,3,5(T₁T₁) states greatly influence the outcome of SF.

Materials and Methods

Material Synthesis.

TDI₂ and TDI-PdTPP were synthesized as described in the SI Appendix by modifying literature procedures (31, 32).

Steady-State and Transient Optical Spectroscopy.

Absorption spectra were collected on a Shimadzu 1800 spectrophotometer. The experimental fsTA and nsTA setup has been previously described (11). Pump pulses at 655, 670, and 685 nm were generated by using the output of a laboratory-built collinear optical parametric amplifier to excite solution samples.

MFE Measurements.

Magnetic field-dependent TA spectra were acquired using the Ultrafast Systems Helios/EOS spectrometer described above modified to route the signal probe through a C-frame dipole electromagnet (model 3480; GMW Inc.). Following interaction with the sample at the center of the field, the probe was directed back into the Helios/EOS spectrometer using specific mirrors and lenses based on the specific probe source, as dictated by the spectral and temporal range being investigated (SI Appendix, Fig. S1). The field strength was monitored at the pole face with a Hall probe and controlled through active feedback between the Gaussmeter (model 475 DSP; Lakeshore Cryotronics, Inc.) and the 1-kW bipolar power supply (BOP-36–28MG; Kepco Inc.). For static fields, the field was set manually and the TA experiments were performed as described above. For field-swept MFE experiments, the field was automatically stepped in 10-mT increments; TA spectra were acquired with 100 logarithmically spaced time points, randomly sampled over the specified time range for 3 minutes per field point.

EPR Spectroscopy.

X-band (∼9.6 GHz) measurements were made using a Bruker Elexsys E680-X/W EPR spectrometer outfitted with a split-ring resonator (ER4118X-MS3). Samples were photoexcited with 7-ns, 2-mJ pulses generated by an optical parametric oscillator (Spectra-Physics Basi-scan), pumped with the output of a frequency-tripled neodymium-doped yttrium aluminum garnet laser (Spectra-Physics Quanta-Ray Lab 170). TREPR spectra were collected following photoexcitation; the kinetic traces of the transient magnetization were acquired in quadrature under continuous wave irradiation (5 mW). Q-band measurements were collected on a homebuilt instrument utilizing a custom-designed Microwave Bridge from Millitech Inc. and equipped with a Bruker EN 5107D2 resonator.

Steady-State and TRF Spectroscopy.

Steady-state fluorescence spectra were collected on a Horiba Nanolog fluorimeter. TRF data were collected with a Hamamatsu C4334 Streakscope streak camera system using a 20-ns window with an IRF of ∼350 ps (FWHM). Excitation pulses (600 nm at 1 nJ per pulse) were generated with a commercial direct-diode-pumped 100-kHz amplified femtosecond laser (Spirit 1040; Spectra-Physics) whose 1,040-nm fundamental beam pumped a noncollinear optical parametric amplifier (Spirit-NOPA; Spectra-Physics).

Computational Details.

Using QChem (version 5.0), optimized ground- and excited-state geometry calculations were performed using DFT and TD-DFT at the Perdew–Burke–Ernzerhof (PBE) PBE0/6-31G* level. Computations were completed on a simplified TDI₂ with CH₃ groups replacing the C₁₅H₃₁ groups at the imides and N,N-dimethyl TDI. Full structures of all calculations are provided in the SI Appendix.