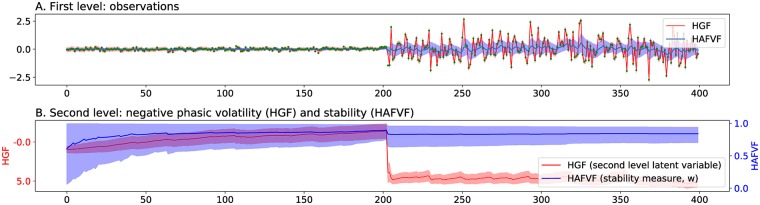
Fig 1. Fitting of HGF model on dataset with changing variance.
Two signals with a low (0.1) and high (1) variance were successively simulated for 200 trials each. A two-level HGF and the HAFVF were fitted to this simple dataset. A. The HGF considered the lower variance component as a “tonic” factor whereas all the additional variance of the second part of the signal was assigned to the “phasic” (time-varying) volatility component. This corresponded to a high second-level activation during the second phase of the experiment (B.) reflecting a low estimate of signal stability. The corresponding Maximum a Posteriori (MAP) estimate of the HAFVF had a much better variance estimate for both the first and second part of the experiment (A.), and, in contrast to the HGF, the stability measure (B.) decreased only at the time of the change of contingency. Shaded areas represent the 95% (approximate) posterior confidence interval of the mean. Green dots represent the value of the observations.