Colloidal Model for the Prediction of the Extraction of Rare Earths Assisted by the Acidic Extractant

Abstract

We propose the statistical thermodynamic model for the prediction of the liquid–liquid extraction efficiency in the case of rare-earth metal cations using the common bis(2-ethyl-hexyl)phosphoric acid (HDEHP) extractant. In this soft matter-based approach, the solutes are modeled as colloids. The leading terms in free-energy representation account for: the complexation, the formation of a highly curved extractant film, lateral interactions between the different extractant head groups in the film, configurational entropy of ions and water molecules, the dimerization, and the acidity of the HDEHP extractant. We provided a full framework for the multicomponent study of extraction systems. By taking into account these different contributions, we are able to establish the relation between the extraction and general complexation at any pH in the system. This further allowed us to rationalize the well-defined optimum in the extraction engineering design. Calculations show that there are multiple extraction regimes even in the case of lanthanide/acid system only. Each of these regimes is controlled by the formation of different species in the solvent phase, ranging from multiple metal cation-filled aggregates (at the low acid concentrations in the aqueous phase), to the pure acid-filled aggregates (at the high acid concentrations in the aqueous phase). These results are contrary to a long-standing opinion that liquid–liquid extraction can be modeled with only a few species. Therefore, a traditional multiple equilibria approach is abandoned in favor of polydisperse spherical aggregate formations, which are in dynamic equilibrium.

Introduction

An increasing usage of rare earth elements (REEs) in new technologies and clean energy production demands the urgent need to improve the current methods for separation from ores and for recycling from used parts and scraps.¹⁻³ The most widely used method in REEs recovery on an industrial scale is liquid–liquid extraction, where the organic phase (the solvent) containing a particular extractant molecule is mixed with an aqueous solution containing target cations (the feed). Beside in hydrometallurgy, liquid–liquid extraction is used to separate minor actinides from REEs in used nuclear fuels.⁴⁻⁹

One of the most commonly used extractants is bis(2-ethyl-hexyl) phosphoric acid, that is, HDEHP.^2,9−11 HDEHP is a part of a class of ion-exchange extractants, as they dissociate upon binding of the target cation. This extractant is often referred under other names such as D2EHPA, DEHPA, or P204, depending on the field of application. HDEHP and acidic extractant systems in general were intensively studied from both experimental and theoretical aspects. The experimental studies include speciation of both phases at equilibrium, scattering techniques, kinetic studies, recent X-ray methods of the liquid–liquid interfaces, and numerous other attempts to clarify the aggregation phenomena.^6,12−21

A little less abundant, but still substantial, is the amount of the literature on theoretical considerations of liquid–liquid extraction using acidic extractants. Studies range from quantum chemistry calculations and molecular dynamics (MD) simulations to macroscopic models based on chemical equilibria. Quantum chemistry calculations are very accurate in determining the composition and associated energy of the first sphere of electron donor atoms around the extracted multivalent cation.²²⁻²⁴ The calculations are often coupled with extended X-ray absorption fine structure measurements to estimate the coordination numbers of the cation in the core of the aggregate.^25,26 Nevertheless, quantum chemistry calculations are limited to a small number of atoms. Therefore, there is no possibility to study the influence of the organic solvent, the length of the extractant chains, and the branching of chains on the overall extraction efficiency.²⁶ MD simulations are convenient and very accurate when studying the solvent and extractant effects.^23,27,28 Moreover, for larger calculation boxes used, it is possible also to obtain a proper structure and organization of the solvent phase and to quantify the supramolecular interactions between the aggregates.²⁹⁻³¹ Still, calculations are possible for limited compositions of the system and reduced variety of modeled species (e.g., the common MD problem with the modeling of the proton transfer).³² Moreover, it is very difficult and computationally expensive to go from the structure of the organic phase to the prediction of the extraction process needed for chemical engineering. For the prediction of extraction, far more practical are macroscopic models based on the chemical equilibrium.^33,34 The advantage of this kind of modeling is the fact that extraction isotherms are obtained. Therefore, a potential of scale-up to chemical engineering arises. Modeling based on chemical equilibria so far has been focused on establishing all possible equilibria and then fitting the constants around the working point.¹² Intrinsically, this way has to work, but it is more a fitting than a real prediction. Furthermore, any perturbation of the system in terms of concentrations of ions and extractants often leads to poor predictions. Consequently, it is not possible to generalize the method and to use the obtained constants for the prediction of extraction of a similar system. The water co-extraction and the organic solvent influence, as well as the length and branching of the extractant chains, are neglected.^9,35 Traditionally, the extraction (i.e., the transfer of ions between two phases) was identified as (or attributed to) the energy of a similar complex between a multivalent cation and electron donor atoms representing the extractant head groups.^36,37 Note that such considerations are only able to provide a qualitative description of the extraction trends, but they fail completely in quantitative assessment.³⁸

To fill the gap between more accurate quantum chemistry calculations and MD simulations at one end and modeling based on chemical equilibria at the other, we developed a simple statistical thermodynamic model coupled with the concepts of colloid self-assembly. This simplified picture of the extraction system allowed us, at the thermodynamic limit, to calculate the actual efficiency of extraction while still keeping the molecular aspect of all constituents involved. Our methodology is based on the evaluation of the free energy of a particular reverse micelle (the aggregate) in an organic solvent.³⁹ The free energy is then a sum of different contributions known from basic and colloid chemistry. This approach (opposite to establishing equilibrium constants) enables us to complete the mass action law (MAL) and paves the road for the determination of every thermodynamic property of the system. This work on acidic, that is, ion-exchange, extractants represents the extension and therefore a generalization of our methodology that was first derived for the case of nonionic extractants.³⁹ Additional phenomena, such as the dimerization and the dissociation of acidic extractants, have been taken into account.

Liquid–liquid extraction involves always a concentrated solution of salts and one complex fluid, most often the solvent phase. In the 1960s, the multiple equilibrium model was developed for any self-assembling system producing aggregates when concentrated.⁴⁰ The difficulty with this model is that it has no practical predictive power because each aggregate of a particular composition is associated to at least one parameter. As the aggregates differ by the aggregation numbers, water content, and the number of extracted cations, large matrices of adjusted constants are generated. Therefore, its practical use is diminished. For extractants, the association can be replaced by an explicit form of free energy; however, this requires the knowledge of quantities such as preferential solvation that are difficult to determine with the precision.⁴¹ However, it is clear that the fluid instabilities and phase separations observed can only be understood if all the aggregates present are considered as species in dynamic equilibrium.⁴² Approximating all aggregates as spheres allows the explicit calculation of all energy terms. The calculations show that the simple stoichiometry has to be abandoned and replaced by the distribution of aggregate sizes. A simplest map refers to the number of water molecules in the polar core and number of complexing agents.⁴³ The ienaic approach lies in between these two extremes. It decomposes the free energy associated to the ion transfer between nearest neighbor interactions (the supramolecular complexation) from all the other terms.⁴⁴ The predictive power of this decomposition has been illustrated successfully in three cases with a focus on the simple case of one uncharged complexing extractant without any synergy.^38,45,46 An explicit parametric study has shown in the case of uncharged extractant that this ienaic approach is able to link quantitatively the observed free energy of transfer controlling the yield of the process to the complexation free energy that is determined in supramolecular chemistry.³⁹ This ienaic approach, evaluating the various relevant interactions is extended here to the common case of acidic extractants. We use as model the well-documented case of HDEHP, a commonly used anionic extractant that has branched chains. Note that HDEHP is in the category type-II B in the classification of organized molecular systems that is currently organized in 17 categories depending on the different behaviors versus pH and water co-extraction for which no predictive theory currently exists.¹²

The overall idea is to bridge the chemical engineering with the models used in fundamental science research. Within this work, we will present a detailed derivation of our model which we will then compare with the experimental data to validate it. It will be shown how the model captures some of the very specific properties of systems employing acidic extractants. At the very end, we will propose a preliminary study concept for chemical engineering to assist a more accurate extraction formulation design. Our model is applicable to both hydrometallurgy and nuclear industry. Note that in hydrometallurgy saponified HDEHP can be used. This case can also be studied within our general framework; the only difference is to add an additional cation in the system, that is, the activity of water and ions changes. To address to a broader audience, we have chosen a well-studied system: the dodecane solvent with dissolved HDEHP in contact with aqueous solution of Eu(NO₃)₃ and HNO₃.

Theory

HDHEP Extraction of Lanthanides—Model

The model system is made of two phases in contact, namely the aqueous phase and the organic phase i.e., the solvent. The aqueous phase can contain multiple ionic species, whereas the solvent phase at equilibrium is made of dispersed monomers, dimers of the extractant, and the self-assembled reverse micelles (i.e., aggregates). The extractant considered within this study is bis(ethylhexyl) phosphoric acid (HDEHP). We have neglected the hydrophilicity of the extractant, as we will be dealing with a system of concentrated aqueous solutions of trivalent cations.^31,47 All aggregates are assumed to be spherical on average, but they differ in sizes.^48,49 In this article, we will focus on the practical system of an aqueous phase containing HNO₃ and Eu(NO₃)₃, whereas the solvent phase is dodecane with dissolved HDHEP extractant (Figure 1). The model is valid for any hydrometallurgical or industrial process as long as spherical aggregates are experimentally observed in the region of the phase diagram. We consider the following set of chemical reactions

1

2

3

4

5

where H2O, Eu3+, H+, NO3–, , , 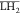and are respectively the symbols for water, the europium cation, the proton, the nitrate anion, the monomeric form of the extractant, the dimeric form of the extractant, and the aggregate of the particular composition. NH2O, NEu3+, NH+, NNO3−, NLH, NL–, and NLH,R are respectively the stoichiometric numbers of extracted water molecules, europium cations, hydrogen ions (protons), nitrate anions, monomeric extractant (the aggregation number), dissociated extractant molecules in the aggregated form, and undissociated extractant in the aggregated form. The species present in the solvent are denoted by overlined symbols.

Figure 1.

Schematic representation of the extraction process. Various types of aggregates are present in the solvent, and their probability at equilibrium is determined by the composition of their cores. Considering the surfactant nature of the extractant, the interface is at least partially covered by the extractant molecules (not shown here). The zoomed region shows the core of the aggregate with the europium cation, the nitrate anion, and the extractant head groups, i.e., phosphate groups.

Free Energy of the Aggregate

Note that the stoichiometry of the released proton is the same as that of the dissociated extractant, N_L^–, as it originates from it. N_LH,R is a residue or the difference between the aggregation number and the dissociated extractant that forms a complex with the metal cation (N_LH,R = N_LH – N_L^–). To preserve the generality of the model, every composition of the aggregate is allowed as long as the electroneutrality of the aggregate is respected. Therefore, together, all equations represent a system of mutually competing chemical reactions. Note that the first reaction (eq 1) represents a dimerization of extractant molecules in the solvent and is included in MAL to adjust the concentration of the monomeric extractant.

Before writing the above chemical reactions in terms of chemical potentials, we need to define and calculate the standard chemical potential of an aggregate of a particular composition. The standard chemical potential of the aggregate 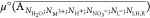(shortly μ_Agg,x^°) is defined as the Helmholtz free energy F_Agg,x of a single aggregate at infinite dilution in a particular organic solvent

6

F_Agg,x can be written as

7

where F_extr. film is the free energy associated with the layer (or a highly curved film) of extractant molecules.³⁸F_core is the free energy of the core of the aggregate and is defined as

8

In eq 8, F_droplet is the free energy of a droplet of aqueous electrolyte solution, F_complex is a term which describes the interactions between the extracted solutes and extractant head groups, and F_correction is the correction of statistics for the small number of particles. F_core will be derived and discussed later in the section. F_extr. film can be written as

9

where F_chain represents the free energy of extractant chains because of the steric effects and is repulsive by nature, and F_exc. head is defined as the excess free energy of mixing two distinguishable head groups into a two-dimensional (2D) plane.⁵⁰

F_chain has a form of a harmonic approximation and can be written as^27,51

10

where N_LH is again the aggregation number, κ* represents the generalized bending constant per molecule in the extractant film, p is the packing parameter of the extractant molecule, and p₀ is the intrinsic spontaneous packing parameter for a certain type of extractant in a given solvent. In the case of aggregates containing dissociated and undissociated extractants, where each one is characterized by its corresponding p₀, we define an effective spontaneous packing parameter as

11

where p_0,L^– is the spontaneous packing parameter of the dissociated extractant.⁵²Equation 11 is based on a mean-field approximation. Equation 11 is plugged into Equation 10. If we assume that the length of the extractant chains in the film is constant upon the change of the composition of the core of the aggregate, we can write p in an explicit form as⁴³

12

where l_chain is the average length of extractant chain in the given solvent and the radius of the core R_core is

13

with V_core being the volume of the core of the aggregate. V_core is a function of stoichiometric numbers and molar volumes of the species present in the core and can be written as

14

where N_Cat,i is the number of cations in the core. V_m,Cat,i, V_m,NO3^–, V_m,H2O, V_m,LH,R, and V_m,L^– are respectively the partial molar volumes of cations, nitrate anions, water, protonated, and deprotonated extractant head groups.

The second term in eq 9 takes into account the enthalpic part of the free energy of mixing of two types of polar head groups (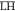 and ) in a monolayer. This excess energy term is derived from the regular solution theory where we considered the 2D array of sites which serve as a representation of the film of polar head groups (i.e. water–oil interface in the aggregates). We have

15

where χ_LH,L^– is the exchange parameter, k_B is the Boltzmann constant, and T is thermodynamic temperature.⁵⁰

With F_extr. film defined, the next step is to calculate F_core.

F_core is already defined as the sum of three contributions, namely the energy of a droplet of aqueous solution F_droplet, the correction of statistics for the case of a small number of particles F_correction, and the complexation energy F_complex (eq 8).

F_droplet is considered as an equivalent system in the bulk. It follows that ions and water molecules inside the core of the aggregate have the same standard state defined as the ones in the aqueous phase in contact. In the case of the liquids, where the PV term is negligible, we can equalize F_droplet ≃ G_droplet. G_droplet can be written as

16

where and μ_j^org are respectively the chemical potentials of water molecules and ions present in the core of the aggregate. Both aqueous solutions inside the core of the aggregate and in the reservoir are considered as ideal. Therefore, we obtain

17

and

18

where μ_j^°, , m_j, m_j^°, x_j, and 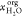are respectively the standard chemical potentials of ions and water in the core of the aggregate, the molal concentration of ions in the core, the molal concentration of ions at the standard state, and the mole fraction of ions and water in the core. Eq 18 is the consequence of eq 17 when Gibbs–Duhem relation is used.

F_complex is the energy term which describes the interaction between the complexed ion and the extractant head groups. In our formulation, it is taken into account as a primitive general description of the complex between the cation and electron donor atoms, which is sometimes referred as a basis of the extraction.³⁶F_complex is a quantity, independent of the accessible volume of the monolayer of the extractant head groups. It reads

19

where N_complex is the number of microstates associated with the binding of the cation to the 2D array of sites, N_Cat,i is again the number of particular cations i in the core, N_bond,i is the number of sites required to bind a particular cation to the array of sites, and E_0,Cat,i is the internal complexation energy parameter and represents the energy contribution for each bond created between the cation and the extractant head groups, that is, sites. Therefore, we assumed the additive nature of the internal energy part of the complexation free energy. N_bond,i for any type of cation ranges from 1 to the charge number of the cation. A general formula for N_complex can be derived from basic combinatorics. We approximate a spherical film of extractant molecules as a 2D array of sites. The surface site is deprotonated only if a metal cation binds to it. Sites that bind the cation are mutually indistinguishable but are distinguishable from the empty sites (no cations bound) and the one that binds the extracted acid. The acid can take up only one site, and it does not deprotonate it. We have the general formula

20

where the factor 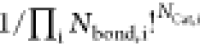accounts for the intra-indistinguishability of sites binding a particle. Note that 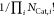is omitted from the calculation as the factor is already intrinsically included within the calculation of F_droplet (eq 16). It can be noticed that the number of microstates associated with the binding of the cation to 2D array of sites, N_complex, differs from the number of microstates associated mixing of the two distinguishable sites in the plane by a factor 1/N_L^–!. –k_BT ln(1/N_L^–!) factor is therefore added to the expression for the standard chemical potential of the aggregate.

The last term in the calculation of the free energy of the core of the aggregate is F_correction. In fact, to calculate F_droplet, we have used Stirling’s approximation, which is only accurate for a large number of particles. In our case, the number of particles is often less than 10. Therefore, we impose a correction factor because of the statistics. F_correction is defined as a correction for using Stirling’s approximation and can be computed as

21

where index j accounts for all the ions present in the core (see the aggregate core partition function in the Supporting Information). After applying the natural logarithm rules and sorting all the terms, we end up with the following expression

22

where index j again goes over all the ions present in the core of the aggregate.

This concludes the calculation of the standard chemical potential of the aggregate of a particular composition. The full expression is presented in the Supporting Information.

Calculation of Equilibrium Aggregate Concentrations

This part deals with the calculation of the equilibrium aggregate concentrations for a system of competition reactions written in the beginning of the section (recall eqs 2–5). The chemical potentials of the species involved in the chemical reaction described can be written as

23

24

25

and

26

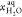where μ_Agg,x, μ_LH, μ_LH^°, c_Agg,x, c_LH, and c° are respectively the chemical potentials, the standard chemical potentials, and the equilibrium molar concentrations and the molar concentrations at standard state of the aggregates and the extractant in the solvent. μ_j, μ_j^°, , x_j, and are respectively the chemical potential of ions, the molal concentration of ions, the chemical potential of water, and the mole fractions of ions and water in the aqueous phase. The chemical potentials of water and ions in the solvent phase have been described in eqs 17 and 18. To complete the calculation, we need to write the chemical reactions (eqs 2–5) in terms of the chemical potentials of all the species involved. We will show the calculation for the case presented by eq 5.

27

which is equal to

28

At this point, it is convenient to define

29

where μ_Agg,x^°″ is the reduced standard chemical potential of the aggregate, obtained by subtracting the chemical potentials of ions and water confined in the aggregate’s core from μ_Agg,x. μ_Agg,x^°″ still contains all other terms, namely the chain, the complexation, the terms for the correction of statistics for small number of particles, the excess internal energy of the mixed protonated/deprotonated extractant film, and the factor quantifying the difference between the number of N_complex and the number of microstates associated with the arrangement of two distinguishable sites in the 2D array. μ_L^– is the chemical potential of the dissociated extractant (or head groups) and is defined as

30

where 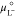and a_L^– are respectively the standard chemical potential and the activity of the dissociated extractant head groups L^–. After inserting eq 29 into eq 28, all the standard chemical potentials of ions and water, except the one of the proton released to the aqueous phase during the chemical reaction, cancel out.

At this point, we can write the aggregation number N_LH as the sum of the dissociated extractant with the bound metal cation and the residual undissociated ones (that can form a complex with the acid or simply constitute a second sphere of the metal cation). If we substitute N_LH with N_L^– + N_LH,R (recall MAL from the beginning of the article) and collect the standard chemical potentials multiplied by N_L^–, we obtain

31

We can identify the term as N_L^– times the standard Gibbs energy of the extractant head group dissociation reaction Δ_rG_a^°, which can be written as

32

where K_a^° is the effective dissociation constant.

By combining eqs 31 and 32, we recover

33

where pH is defined as

34

Note that we have discarded the term k_BT ln a_L^– from the calculation (the term is present in eq 31, whereas it is not present in eq 33). In fact, it can be shown that the term is already intrinsically included within the definition of the complexation energy F_complex (eq 19). In the Supporting Information, we have provided a small phenomenological argument to support this claim.

Now, we multiply eq 33 with β (where β is defined as 1/k_BT) and apply the exponential function to the whole expression. We obtain

35

where B_Agg,x is defined as

36

with

37

In this representation, the calculations are preformed so that each possible aggregate is an element in a matrix, with the element being the concentration at equilibrium c_Agg,x, characterized by eq 35. The dimensionality of the matrix is defined by N_LH, N_H2O, and ∑_iN_Cat,i. The only restraint in the calculation is the condition of the electroneutrality of the aggregate in the organic solvent. Therefore, the stoichiometric numbers of all the charged species in the aggregate core multiplied by their corresponding charge number sum up to 0. We have

38

where z_j and z_L^– are respectively the charge numbers of the ions and dissociated extractant head groups present in the core of the aggregate.

We have established a full framework to calculate the thermodynamic properties of extraction systems by calculating the competition between different aggregates. The calculations are preformed in a Semi-Grand canonical ensemble.⁵³ The flowchart of the developed program is presented in the Supporting Information (Figure S13).

Results and Discussion

Input and the Model Parameters

It was described in the previous section that the derived model requires a certain set of measurable quantities and adjusted parameters to perform calculations. To assemble the core of the aggregate (eq 14), we need partial molar volumes of all species present.⁵⁴ In the case of Eu³⁺, as well as in the case of many trivalent cations, the partial molar volume is close to −40 cm³ mol^–1. This value is the consequence of the electrostriction phenomenon.⁵⁵ In the case of very high ion concentrations, or in confined media, this property is not valid. Therefore, because of the loss of electrostriction in the core of the aggregate, we neglect the Eu³⁺ contribution. The partial molar volumes of the HDEHP polar head groups are considered similar to the partial molar volumes of the phosphoric acid species. The partial molar volume of the protonated form LH is set equal to the molar volume of H₃PO₄, whereas L^–1 is equal to the molar volume of H₂PO₄^–1.^54,56 To calculate the packing parameter of the particular aggregate (eq 12), we need the average length of the HDEHP chains in the film, l_chain. The value used for calculations is l_chain = 4.3 Å and was determined by the combination of small angle X-ray scattering and small angle neutron scattering measurements on the system identical to our study: dodecane solvent containing HDEHP is in contact with the aqueous phase containing Eu(NO₃)₃ and HNO₃.⁴⁹ Besides experimentally, l_chain can also be assessed theoretically by MD simulations in an explicit solvent.²⁷ In the Theory section, by solving the general form of MAL, the derivation yielded the term which represents the effective dissociation constant pK_a^°. For calculations, we used the value pK_a = 2.79, obtained from the literature.^47,57 Note also that various sources report different pK_a^° values.^58,59

To account for the dimerization of HDEHP in the solvent (eq 1), we used log K_D = 4.43, with K_D being the dimerization constant.⁶⁰ This value corresponds to the system of HDEHP dissolved in pure dodecane with no aqueous phase in contact. Only this value should be used because whenever there is a water phase in contact, there is certain aggregation which creates an error upon the determination of log K_D.^22,23 Moreover, the reported values of log K_D show a strong dependence on both the composition of the aqueous phase and the type of the organic solvent.^57,61

With the measured quantities described, we turn our intention to the adjusted parameters of the model. The physics and the influence of each of the parameter on the properties of the extraction systems have been already described and discussed individually in the section Theory. A detailed description of the influences can be also found in our previous publication.³⁹

Here, we will present the procedure of adjusting the model parameters. We compared our model with an experimental study which dealt with an identical system as ours. HDEHP is dissolved in the analytical grade dodecane, and the aqueous phase is made of, respectively, pure water, nitric acid, and europium nitrate in nitric acid.^62,63

Note that we performed fitting under constraints to reduce the number of possible sets of parameters that reproduce the experimental data. Constraints are such that, besides the extraction isotherms, we ought to recover experimentally observed critical aggregate concentration (CAC) of particular system in the study and that realistic aggregate compositions are obtained. Also, it is important that the prediction of extraction is invariant to the upper value of aggregation number and water content used in the calculations.³⁹ Moreover, it is crucial to start the fitting from the simplest system of pure water extraction only and then to consider more complex systems containing HNO₃ and Eu(NO₃)₃, respectively.

In this sense, first, we fitted the model to the system of pure water in contact with the solvent containing HDEHP, as can be seen from Figure 2a. To recover the experimental value, we needed to adjust the HDEHP standard chemical potential to μ_LH^° = 12.8 kJ mol^–1, the generalized bending constant to κ* = 14 k_BT, and the spontaneous packing parameter to p₀ = 2.6 of the extractant exposed to pure water. Note that the minimum aggregation number was set to 4. Then, we considered the system of nitric acid, m(HNO₃)_aq,eq = 1 mol kg^–1, in contact with the solvent phase, as presented in Figure 2b. By using the already obtained parameters, we can deduce the complexation energy of the acid, E_0,HNO3. We obtained E_0,HNO3 = 4.2 k_BT, which is the order of magnitude of the typical hydrogen bond. Using the same κ* and p₀ for the HNO₃ system is based on the argument that additional binding of the acid to the extractant head group does not impose any severe structural change to the extractant film (the phosphate group does not dissociate). μ_LH is by definition the free energy of a single HDEHP molecule in a given solvent at infinite dilution. Therefore, μ_LH^° is a constant for any multiphase system.

Figure 2.

Concentrations of solutes in an organic solvent as a function of the initial extractant concentration, c_LH,initial. The solvent phase in contact with (a) pure water, (b) HNO₃ aqueous solution, m(HNO₃)_aq,eq = 1 mol kg^–1, (c) Eu(NO₃)₃, HNO₃ aqueous solution, m(HNO₃)_aq,eq = 1 mol kg^–1 and m(Eu³⁺)_aq,eq = 0.032 mol kg^–1.

For the case of Eu(NO₃)₃ extraction, we have a dissociation of the extractant followed by complexation of the cation. In this case, there is a change in p₀, and we need to fit it accordingly.⁶⁴ When Eu³⁺ is bound to the extractant, p₀ = 3.5. It can be concluded that the HDEHP chains take up a larger volume (the chains are more spread) when there is a trivalent cation present inside the core, compared to the case of aggregates filled with acids only. The effective spontaneous packing parameter, p_0,eff, is calculated assuming a mean-field approximation for a mixture of LH and L^– in the extractant film. As before, we also deduce E_0,Eu³⁺ = 20.4 k_BT per bond. Note that upon the dissociation of the head groups, we create new types of sites in the extractant film. As was written in the section Theory, the creation of distinguishable sites has associated free-energy contribution, F_exc. head (eq 15). We have accounted for this phenomenon by generalizing a regular solution theory on a 2D film. With the entropic part of the associated free energy already being included within the F_complex (recall eqs 19 and 20), we needed to adjust the enthalpic contribution of F_exc. head, which is described by χ_LH,L^–. Within the fitting procedure, we obtained χ_LH,L^– = 0.5k_BT which points to the fact that there is a repulsive force between the dissociated and undissociated extractant head groups. This contribution, along with the energy associated with the dense packing of the extractant chains F_chain, works in the opposite direction compared to the complexation, thus quenching the extraction of solutes. The minimum aggregation number for the case of Eu³⁺ was 6. Such an aggregation number is often reported in the literature (6 monomers or 3 dimers).^6,31 This monodispersity in terms of aggregation number is contrary to the case of nonionic extractants where polydispersity is severe in both the aggregation number and the water content.^28,65 The difference is due to the stronger interaction between the dissociated extractant groups and the trivalent cations in the case of acidic extractants.

To derive eqs S7 and S1 in the Supporting Information, we needed to ignore any influence of the composition of the polar core of the aggregate on the lateral interactions between extractant head groups (see the partition function of the core of the aggregate in the Supporting Information). The only interaction potential is given as the complexation energy and accounts for the interactions of head groups and complexed multivalent cation or the acid. This is a severe simplification. Consequently, it was mandatory to study the influence of χ_LH,L^– on the actual efficiency of extraction.

Therefore, in Figure 3 we plotted the negative value of the natural logarithm of the Eu³⁺ distribution coefficient −ln D_Eu³⁺ (the scale is not prone to large variation) as a function of E_0,Eu³⁺ and χ_LH,L^– used for calculations. The distribution coefficient is defined in the Supporting Information. The white region on the graph depicts the experimental values of the Eu³⁺ extraction. It can be seen that the choice of χ_LH,L^– on the extraction data is rather small and is easily compensated by E_0,Eu³⁺, that is, i.e. a dominant factor in the free-energy representation. We can choose χ_LH,L^– from a positive (repulsive character) to negative (attractive character) value, whereas E_0,Eu³⁺ per bond still stays globally the same. This counterintuitive result is convenient because it enables us to omit χ_LH,L^– from the model, thus simplifying the fitting procedure.

Figure 3.

Negative value of the natural logarithm of the Eu³⁺ distribution coefficient, −ln D_Eu³⁺, as a function of the Eu³⁺ complexation energy parameter per bond, E_0,Eu³⁺, and the exchange parameter, χ_LH,L^–, used in the calculations. The white region depicts the experimental data.

For all subsequent calculations (the subject of the following section), we used the described set of parameters at T = 298.15 K. With the input and the parameters of the model derived and discussed, we turn our attention to the calculation of the specific properties of the HDEHP extraction systems such as speciation of the extractant, aggregation regimes, the transfer of different solutes between phases, the apparent stoichiometry, and so forth.⁶⁶

Speciation of the Solvent Phase

We start by analyzing the results presented in Figure 2a–c, where the concentration of the extracted solutes in the solvent phase is plotted as a function of the initial extractant concentration, c_LH,initial. When comparing the results from Figure 2a,b, it can be noticed that upon the addition of HNO₃ to the system, the extraction of water slightly increases. H₂O is mandatory to stabilize the core of the aggregate by the dilution effect, that is, co-extracted water solubilizes the extracted acid by creating a small water pool. Figure 2c shows a slight decrease in H₂O and HNO₃ extraction because now there is a stronger competition reaction of Eu³⁺ extraction present in the system. The model predicts a lower H₂O uptake when multivalent cations are present in the system. This is also demonstrated in Figure S1 in the Supporting Information. In the case of the Eu³⁺ extraction, there are only few water molecules present in the core of the aggregate, whereas HNO₃-occupied cores can contain from two to seven water molecules. The water extraction and its influence on the stabilization of the aggregate core are often reported in the literature.^{20,24,25,67,68}

We used the model to study the speciation of the HDEHP extractant in the solvent as a function of c_LH,initial. In Figure 4, we have plotted respectively the concentrations of monomers, dimers, and the aggregated extractant as a function of c_LH,initial. In our study, we distinguish dimerization from aggregation. Aggregation is the self-assembly of the species into reverse micelles filled with extracted solutes from the aqueous phase. The presented results correspond to the experimental system on which we based our fitting procedure. In the case of m(HNO₃)_aq,eq = 1 mol kg^–1 and m(Eu³⁺)_aq,eq = 0.032 mol kg^–1, we can see that monomeric HDEHP is globally small. This is a consequence of the strong tendency of HDEHP (and most acidic extractants) toward dimerization and aggregation.^6,69 To create monomers, there is a penalty in energy for exposing the polar head groups toward the oil medium. Note that before the experimentally observed CAC, which is reported to be 0.21 mol dm^–3, the concentration of the aggregated HDEHP is moderate. After CAC, there is a pronounced increase in the concentration of the aggregated extractant. This behavior was already reported based on an experimental study.¹³ The speciation of HDEHP through the whole region of c_LH,initial is provided as a log–log graph presented in Figure S2 in the Supporting Information.

Figure 4.

Speciation of the extractant in the solvent as a function of the initial extractant concentration, c_LH,initial. The solvent phase is in contact with m(HNO₃)_aq,eq = 1 mol kg^–1 and m(Eu³⁺)_aq,eq = 0.032 mol kg^–1. Enlarged region at low c_LH,initial is presented in the inset.

Still, describing speciation in a system just around working point (m(HNO₃)_aq,eq = 1 mol kg^–1 and m(Eu³⁺)_aq,eq = 0.032 mol kg^–1) does not provide any new and meaningful insight. The complexity of the extraction systems demands the study of speciation in terms of m(HNO₃)_aq,eq, m(Eu³⁺)_eq,aq, and c_LH,initial. Figure 5a–d shows the aggregated, the dimerized, and the monomeric HDEHP as a function of both c_LH,initial and m(HNO₃)_aq,eq, for m(Eu³⁺)_eq,aq = 0.032 mol kg^–1. The results show a complex aggregation landscape with a few distinct regimes. It can be seen that at low m(HNO₃)_aq,eq and high c_LH,initial, the aggregated extractant form is dominant, whereas both monomeric and dimerized forms are negligible (bottom right corner in Figure 5a–d).

Figure 5.

Speciation of the extractant in the solvent as a function of HNO₃ concentration m(HNO₃)_aq,eq in the aqueous phase and the initial extractant concentration c_LH,monomer in the solvent: (a) aggregated extractant, (b) dimerized, (c) monomeric, (d) equivalent to (c), but the scale is adjusted so that differences in c_LH,monomer can be clearly seen. The europium concentration used for the calculation is m(Eu³⁺)_eq,aq = 0.032 mol kg^–1, and c_LH,initial = 0.6 mol dm^–3.

Eu³⁺-induced aggregation at low m(HNO₃)_aq,eq, which is characterized by a higher aggregation number, leads to the total extractant consumption, that is, the extractant saturation.

A local maximum of the dimerized and monomeric extractant concentrations (or a local minimum in terms of the aggregated HDEHP) occurs around m(HNO₃)_aq,eq = 1.5 mol kg^–1 and it corresponds to quenched Eu³⁺ extraction. There is a slight pure HNO₃ extraction but insufficient to induce the aggregation. For higher m(HNO₃)_aq,eq, the aggregation is again favored and is now controlled by the pure HNO₃ extraction (see Figure S3 in the Supporting Information).

We have also studied aggregation as a function of m(HNO₃)_aq,eq and m(Eu³⁺)_eq,aq for a fixed c_LH,initial = 0.6 mol dm^–3, and the results are presented in Figure S4 in the Supporting Information. It is worth to mention that the aggregation is favored for high m(Eu³⁺)_eq,aq and low m(HNO₃)_aq,eq, whereas an increase in the dimerized HDEHP concentration occurs for higher m(HNO₃)_aq,eq values.

Predicting the Extraction

In this section, we will validate our model by comparing its predictions with the literature. Furthermore, we will investigate the influence of m(HNO₃)_aq,eq and m(Eu³⁺)_eq,aq on the overall extraction efficiency. Also, we will deal with the long-standing discussion of the apparent stoichiometry of the extraction processes and provide new insights for desirable formulations for chemical engineering.

Figure 6 shows the dependence of D_Eu³⁺ on the acid concentration in the aqueous phase, m(HNO₃)_aq,eq. The calculations for various c_LH,initial are presented. Globally, our results are in agreement with the literature.^36,70,71 At low m(HNO₃)_aq,eq the extraction is high, whereas it decreases upon an increase of m(HNO₃)_aq,eq. Within our model, this property is reflected in the −N_L^– ln(10)(pK_a^° – pH) energy term (eq 36). It clearly shows that the difference between the effective pK_a and the ambient pH (in the reservoir) governs the extraction efficiency as one of the leading terms in the free-energy approach.

Figure 6.

Eu³⁺ distribution coefficient, D_Eu³⁺, as a function of HNO₃ concentration in the aqueous phase. Results for the various initial extractant concentrations, c_LH,initial, are presented. The solvent phase is in contact with m(Eu³⁺)_aq,eq = 0.05 mol kg^–1.

When changing c_LH,initial from lower values up to 0.6 mol dm^–3, there is an increase of D_Eu³⁺. This happens because of the fact that higher extractant concentrations in the system can take up higher cation loading. Upon examination of the isotherms, we can see that there is still a pronounced Eu³⁺ extraction in the case of c_LH,initial = 0.15 mol dm^–3. Recall that the experimentally observed CAC is around 0.21 mol dm^–3. It practically means that even below the aggregation threshold, if the acid concentration is sufficiently low, acidic extractants will still extract cations (as reported experimentally⁷²). The phenomenon of extraction below CAC is contrary to the case of nonionic extractants (e.g., amides, malonamides, or diglycolamides).⁷³⁻⁷⁵ For nonionic extractants, the extraction efficiency is strongly dependent on CAC.³⁹

We have studied the dependence of the extracted Eu³⁺ concentration in the solvent on m(Eu³⁺)_aq,eq at c_LH,initial = 0.6 mol dm^–3. Results are presented in Figure 7 for multiple m(Eu³⁺)_aq,eq. We can see that the obtained curves have the shape of Langmuir isotherms with asymptotic behavior at high m(Eu³⁺)_aq,eq. Lower m(HNO₃)_aq,eq again favors higher extraction (pale green lines). Our calculations also show that the acid concentration (or pH) has a stronger influence on the efficiency of extraction compared to the cation concentration in the aqueous phase. This can be seen as a moderate increase in c(Eu³⁺)_org,eq with increasing m(Eu³⁺)_aq,eq, whereas differences in m(HNO₃)_aq,eq impose large differences in c(Eu³⁺)_org,eq.

Figure 7.

Eu³⁺ concentration in the solvent as a function of europium concentration in the aqueous phase, m(Eu³⁺)_aq,eq. Results for various m(HNO₃)_aq,eq and c_LH,initial = 0.6 mol dm^–3 are presented.

The results from both Figures 6 and 7 can be shown in the free-energy representation. Instead of plotting the concentrations of cations in the solvent, we have plotted the negative value of the natural logarithm of the distribution coefficient, −ln D_Eu³⁺, as a function of m(HNO₃)_aq,eq and m(Eu³⁺)_aq,eq, respectively. The value −ln D_Eu³⁺ is historically referred as the apparent energy of transfer. The results are presented in Figures S5 and S6 in the Supporting Information. Figure S5 (analogue of Figure 6) shows that an increase in m(HNO₃)_aq,eq increases the apparent energy of transfer. To lower the apparent energy of transfer (i.e., to boost the extraction of the cation), there must be a compensation in terms of an increase of either c_LH,initial or m(Eu³⁺)_aq,eq in the system. Figure S5 (analogue of Figure 7) shows again the unfavorable influence of the acid by increasing the apparent energy. Note that the curves are divergent, as D_Eu³⁺ diverges at a very low m(Eu³⁺)_aq,eq. A steep decrease in the apparent energy of transfer clearly demonstrates a loss of reversibility of extraction formulations (thus making it undesirable for chemical engineering) at low m(HNO₃)_aq,eq and m(Eu³⁺)_aq,eq and high c_LH,initial.

A so-called slope method is usually employed to study the apparent stoichiometry of extraction. The method is valid if only one equilibrium is considered (no variation of aggregation number, unless it is very dilute), if the activity coefficients of the species are constant, and if the logarithm of the distribution coefficient of the target cation is plotted as a logarithm of free monomers at equilibrium. If the three conditions are fulfilled, the slope corresponds to the apparent stoichiometry, that is,. to the stoichiometric ratio of the average aggregation number and target cation.¹²

Our model is set in a way that it takes into account the dimerization of the extractant and aggregates are formed from monomers. In this case, the slope method should be equal to 6. Indeed, if we plot the logarithm of the europium distribution coefficient log D_Eu³⁺ as a function of the logarithm of free monomers log(c_LH,monomer/c°), the calculated slope is 6 (see Figure S8 in the Supporting Information). The result is consistent with the calculations of aggregate probabilities where polydispersity in terms of water content and monodispersity in terms of aggregation numbers were observed. Furthermore, one may also study the extraction system in terms of dimers forming the aggregate. In this case, the slope should be equal to 3. This was also the result of our calculations for the plotted log D_Eu³⁺ as a function of the logarithm of the dimerized extractant concentration log(c_LH,dimerized/c°) (see Figure S8 in the Supporting Information). In terms of experiments, it is difficult to measure the dimerized and monomeric equilibrium extractant concentrations, but the sum of the two can be measured. In that sense, we can plot log D_Eu³⁺ as a function of the sum of the amount of monomeric and dimerized extractants at equilibrium, log(c_{LH,equilibrium}/c°) with c_{LH,equilibrium} = c_LH,monomer + 2c_LH,dimerized. The results show different slopes depending on log(c_{LH,equilibrium}/c°). The initial slope is now 4, and it corresponds to the average of the slopes for monomeric and dimerized extractants. In the case that log(c_LH,initial/c°) is plotted, then the differences in the apparent stoichiometry regimes are even more pronounced and more difficult to interpret (see Figure S8 in the Supporting Information). Moreover, the situation is especially bad when a part of HDEHP (or any hydrophilic extractant) is involved in the equilibrium with HNO₃ and H₂O.³⁹ To treat these complicated situations, one needs a proper speciation of the organic phase for any experimental condition (Figures 5 and S4). Our model can help get a correct apparent stoichiometry in case of nonionic extractants, as well as ion-exchangers.

Overview of the Extraction and Desirable Formulations

It was hinted in Figure 5 and emphasized through Figures 6–8 that there is a diversity of regimes in the HDEHP extraction system. Like in the previous section, we made a more complete study of the extraction by calculating the concentrations of all extracted solutes in the solvent phase and CAC as a function of both m(HNO₃)_aq,eq and m(Eu³⁺)_aq,eq for c_LH,initial = 0.6 mol dm^–3. Figure 9a–c shows the extraction maps of Eu³⁺, HNO₃, and H₂O, whereas Figure 9d shows a map of CAC. It is important to emphasize that we provided our definition of CAC because of the fact that experimental techniques provide large errors upon determination.⁴⁹ We have defined CAC as a concentration after which aggregation is in a linear regime. The method we used to calculate CAC is provided in the Supporting Information (Figure S11). Defining CAC in organic solvents can be arbitrary, but once defined, it should be used as a reference when comparing deviations from it (comparable to the standard state in general thermodynamics).

Figure 8.

Decimal logarithm of Eu³⁺ distribution coefficient as a function of the sum of the amount of monomeric and dimerized extractants at equilibrium, log(c_{LH,equilibrium}/c°); c_{LH,equilibrium} = c_LH,monomer + 2c_LH,dimerized. The results for various m(HNO₃)_aq,eq and m(Eu³⁺)_aq,eq = 0.01 mol kg^–1 are presented.

Figure 9.

Concentrations of the extracted solutes (a–c) and CAC (d) in the solvent phase as a function m(Eu³⁺)_aq,eq and m(HNO₃)_aq,eq. Results are presented for the case of c_LH,initial = 0.6 mol dm^–3. The inset in (a) shows an enlarged region of the pronounced Eu³⁺ extraction.

Figure 9a–d shows a complex extraction and aggregation landscape of the HDEHP system.

It can be seen in Figure 9a that a high Eu³⁺ extraction corresponds to m(HNO₃)_aq,eq lower than 1.5 mol kg^–1. A higher m(HNO₃)_aq,eq completely blocks Eu³⁺ extraction. The blocking HNO₃ effect can be partially compensated with the increase of m(Eu³⁺)_aq,eq, as can be seen by the broadening of the Eu³⁺ extraction region (a pale blue color). This is the first major difference that is hard to detect by plotting a series of 2D graphs. By increasing the chemical potential of Eu³⁺, we can increase the working range in terms of m(HNO₃)_aq,eq. The calculations also predict that a high Eu³⁺ extraction region is accompanied by less H₂O uptake and HNO₃ extraction (blue region in Figure 9b,c). Yet, when m(HNO₃)_aq,eq is sufficiently high (after 1.5 mol kg^–1), the acid extraction takes hold. Consequently, the water uptake increases. Practically, it means that the extractant is consumed not to extract the target cation but is spent on the pure acid extraction. This case obviously represents an undesired industrial formulation. In the case when both m(HNO₃)_aq,eq and m(Eu³⁺)_aq,eq are high (right upper corners of the extraction maps), HNO₃ extraction is even more pronounced. At these conditions, we have saturated the aqueous phase with salts. Therefore, chemical equilibrium is shifted toward relaxation in terms of HNO₃ transfer to the solvent (as Eu³⁺ extraction is impossible because of high m(HNO₃)_aq,eq). The water uptake (Figure 9c) follows the same trend to stabilize the core of the aggregates with multiple HNO₃ present inside. It is worth emphasizing that the water content around the working point (m(HNO₃)_aq,eq ≈ 1 mol kg^–1, m(Eu³⁺)_aq,eq ≈ 0.05 mol kg^–1) stays globally constant up to a moderate m(HNO₃)_aq,eq level. Upon an additional increase of m(HNO₃)_aq,eq, an abrupt water co-extraction occurs. This is demonstrated in Figure S10 in the Supporting Information. It must be emphasized that our model overestimates H₂O and HNO₃ extraction, but the order of magnitude is correct. This is a consequence of the fact that we neglected activity correction in the aqueous phase, which means that within the model, these issues can be easily solved. Also, Eu³⁺ extraction at very low m(HNO₃)_aq,eq shows an abrupt increase. We have traced the issue down to the error of the V_core calculation where we have neglected the partial molar volume of Eu³⁺. By doing so, we diminished the energy penalty, F_chain, upon swelling the aggregate core. This can also be solved by taking the tabulated values of molar volumes of mixed salts at finite concentration. With the drawbacks of the model emphasized, we must add that around the working point of the industrial processes, the model shows remarkable prediction power and the results are in agreement with the experimental data (as was seen from the previous section). These drawbacks appear only at the borderlines of the phase diagram, where we cannot even apply the model of the spherical micelles.

When it comes to the design of a desired reversible formulation, knowledge of the aggregation behavior is crucial because it affects the other properties important for industrial applications such as viscosity.

In that sense, we have studied the CAC dependence of the composition of the system (Figure 9d). Note that this graph is complementary to the graphs in Figure S4 in the Supporting Information. While inspecting Figure 9d, it can be seen that the aggregation (regions of lower CAC) is controlled by two different competition reactions, that is, Eu³⁺ extraction at low m(HNO₃)_aq,eq and pure HNO₃ extraction at high m(HNO₃)_aq,eq. Around the working point, the CAC landscape has a shape of a hill, with the slopes descending toward the Eu³⁺ and HNO₃ extraction regions. “The CAC hill” (i.e., the minimum of the aggregation) corresponds to the case of poor Eu³⁺ extraction because of the presence of HNO₃, but the HNO₃ concentration itself is not high enough to induce the aggregation by the pure acid extraction. This region of high CAC is manageable and therefore appropriate in the industry as it should correspond to the formulation of a moderate viscosity. The last thing to note here is that at high m(Eu³⁺)_aq,eq and low m(HNO₃)_aq,eq CAC is of the order of magnitude on a millimolar scale (the blue region in Figure 9d). This means that we have saturated completely the extractant and we are in the danger of the third phase formation. A question also arises here: with this being a thermodynamically strongly favored extraction, how effective will be the stripping in the next stage of the cation recovery? Indeed, it was this issue that induced the development of the less efficient HDEHP extractant analogues.²

Our model predicts that the design of the most appropriate extraction formulation would correspond to the region between m(HNO₃)_aq,eq ≈ 0.5 and 1 mol kg^–1 and m(Eu³⁺)_aq,eq ≈ 0.1 and 0.2 mol kg^–1. Such formulations would have a reversible extraction character, while exhibiting moderate viscosity and no danger to the third phase formation, that is, around half of the extractant is in the form of dimers and not in a fully aggregated form.

Complexation Energy and Formulation Design

In the previous section, we have discussed the efficiency of extraction and aggregation with respect to the concentrations of all constituents. Yet, we did not comment on the choice of the extractant molecule itself.

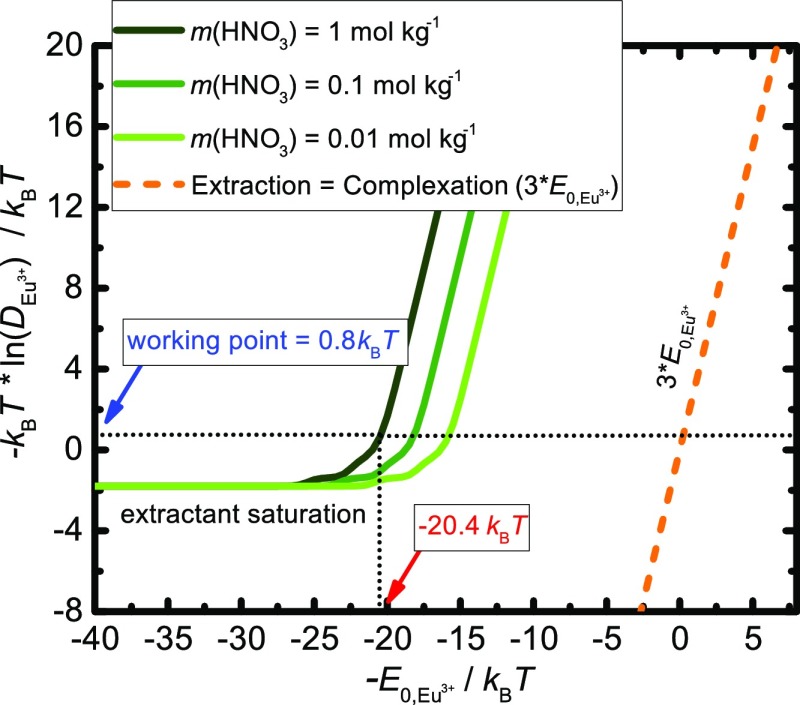
Within the model, the interaction between the extracted cation and the particular extractant molecule is described by the adjusted parameter E_0,Eu³⁺. It reflects the affinity of the extractant molecule toward the target cation. Therefore, every cation/extractant molecule pair has its associated E_0,Eu³⁺. If we set E_0,Eu³⁺ as a continuous variable, then we can artificially represent different types of the possible extractants for the design of the extraction formulation. Figure 10 shows the negative value of the natural logarithm of the Eu³⁺ distribution coefficient, −ln D_Eu³⁺, as a function of the negative value of the complexation parameter per cation/extractant bond, −E_0,Eu³⁺, for three different m(HNO₃)_aq,eq, at m(Eu³⁺)_aq,eq = 0.05 mol kg^–1 and c_LH,initial = 0.6 mol dm^–3. The negative values of E_0,Eu³⁺ are taken for the purpose of visually easier understanding of the context. As we wrote in the previous section, −ln D_Eu³⁺ is historically referred to as the apparent energy of transfer of the cation between two phases. The results show two distinct regimes for any concentration of m(HNO₃)_aq,eq. At low −E_0,Eu³⁺ (which represents a highly favorable interaction between the extractant and the cation), the apparent energy of transfer is constant. This regime corresponds to the complete saturation of the extractant, that is, the saturation threshold. It shows that practically we do not need to use a stronger complexing agent (the extractant) to improve the efficiency of extraction. The limit of extraction is given by m(Eu³⁺)_aq,eq to c_LH,initial ratio.³⁹ For higher −E_0,Eu³⁺ values (the lower affinity of the extractant to cation), the apparent energy of transfer increases, which means that these types of extractants will be less efficient for the extraction formulation design. Now if we change m(HNO₃)_aq,eq in the system, the results show that the saturation threshold will occur at lower −E_0,Eu³⁺ for higher m(HNO₃)_aq,eq in the aqueous phase (the lower pH). By decreasing m(HNO₃)_aq,eq, the saturation threshold occurs at higher −E_0,Eu³⁺. These results are the consequence of the pK_a° – pH term which gives a distinct functionality of the extraction isotherms. Note that the weak extraction regimes of all three curves are equidistant after the saturation threshold (the curves are separated by the factor −N_L^– ln(10)(pK_a^° – pH)). A strong influence of m(HNO₃)_aq,eq on the apparent energy of transfer gives chemical engineering more liberty in the design of the extraction formulation. If the goal is to extract the same amount of Eu³⁺ like around the working point, one can use a less efficient extractant (characterized by higher −E_0,Eu³⁺ values) at a higher pH in the aqueous phase.

Figure 10.

Apparent energy of Eu³⁺ transfer as a function of the negative value of the complexation energy parameter per bond, −E_0,Eu³⁺. The negative values of E_0,Eu³⁺ are taken for the purpose of visually easier reading of the saturation limit. Results for various m(HNO₃)_aq,eq are presented at m(Eu³⁺)_aq,eq = 0.05 mol kg^–1 and c_LH,initial = 0.6 mol dm^–3. The dashed orange line represents the assumption that the apparent energy of transfer is equal to the total complexation energy in the aggregate.

We have emphasized throughout the article that the system in study shows a complexity of extraction regimes. Therefore, we calculated complementary maps of the apparent energy of transfer as a function of m(Eu³⁺)_aq,eq and −E_0,Eu³⁺ for three m(HNO₃)_aq,eq. The results are presented in Figure 11a–c. The white dashed region on the maps depicts the extraction efficiency of the working point. The low −E_0,Eu³⁺ and m(Eu³⁺)_aq,eq region corresponds to the extractant saturation threshold, as can be seen as a dark blue plateau for any m(HNO₃)_aq,eq. After the working point region, a steep increase in the apparent energy of transfer occurs (as was demonstrated also in Figure 10). The results again show that m(HNO₃)_aq,eq has a pronounced effect on the choice of −E_0,Eu³⁺ to achieve the extraction efficiency of the working point. By decreasing m(HNO₃)_aq,eq, the higher −E_0,Eu³⁺ values (a weaker extractant) are sufficient for the reversible formulation. Another aspect shown in Figure 11a–c is worth to comment. The dotted rectangle enclosing the white dashed region is given as a guideline. It must be emphasized that the working point region broadens upon the increase of m(HNO₃)_aq,eq. We have already shown throughout the article that these conditions correspond to the flat top of the aggregation, “the hill”. This gives chemical engineering even more liberty in the design of the extraction process.

Figure 11.

Negative value of the natural logarithm of the Eu³⁺ distribution coefficient, −ln D_Eu³⁺, as a function of −E_0,Eu³⁺ and m(Eu³⁺)_aq,eq. The results are presented for various m(HNO₃)_aq,eq for c_LH,initial = 0.6 mol dm^–3. The white region depicts the experimental data. The dotted rectangle enclosing the white region is given as a guideline to depict its broadness.

In our approach of the aggregate free-energy calculation and completing the MAL afterward, the calculated apparent free energy of transfer corresponds to the interplay of the energy contributions. The leading complexation energy term (characterized by E_0,Eu³⁺) shifts the equilibrium toward the extraction of cation to the solvent but is counterbalanced by few terms. Terms like the energy penalty for the formation of the highly curved film of the extractant chains F_chain (eq 10), lateral head group repulsions in the extractant film F_exc. head (eq 15), differences in the ion concentrations and water activities between the core of the aggregates and the aqueous phase, and the difference between an effective pK_a^° and low pH oppose the complexation or the competing HDEHP dimerization. The sum of all contributions yields the apparent energy of transfer (dotted black line). The apparent energy of transfer for any m(HNO₃)_aq,eq is far from the assumption, extraction = complexation (dashed orange line in Figure 10). Once −E_0,Eu³⁺ is high enough and unable to push the equilibrium toward the solvent phase with respect to the opposing quenching terms, the slope of the calculated apparent energy of transfer is equal to the dashed orange line. This regime of weak extraction is no longer interesting for chemical engineering.

Naturally, we made a map of the apparent energy of transfer as a function of m(HNO₃)_aq,eq and −E_0,Eu³⁺. The results are presented in Figure S11 in the Supporting Information. Once again, the results reflect the complexity of the extraction systems as we have multiple solutions in the design of the extraction formulation, just by changing the concentration of the acid.

Examining the results in Figure 10 reveals another important aspect of the aggregation phenomenon, leading the extraction of cations to the solvent. We have already stated that extraction is sometimes identified as the complexation of the cation by the chelating agent, where the chelating agent represents the extractant molecule. In such representation, the apparent energy of transfer corresponds to the difference between the energy of similar complex (cation and chelating agents) and the hydration energy of cation in the aqueous phase (the first sphere interactions in both examples). If extraction can be identified as a simplified picture of complexation only, then the calculated apparent energy would correspond to the dashed orange line in Figure 10. The line has a value of 3 times −E_0,Eu³⁺, as the mentioned assumption deals only with the total complexation energy (note that the abscissa values are in −E_0,Eu³⁺ per bond). The intersection of the dashed orange line with the horizontal dotted black line represents the extraction around the working point in chemical engineering, and it corresponds to −E_0,Eu³⁺ less than k_BT per extractant/cation bond. Such a small excess first sphere interaction energy between Eu³⁺ and the dissociated HDEHP head group cannot account for the transfer of the cation to the solvent phase. It would completely neglect any colloidal aspect, reverse micelle formation, or the influence of the organic solvent. Moreover, it would imply that the energy of the first sphere around the multivalent cation which includes three charged ligands (plus uncharged ligands and water molecules) is almost equal to the hydration energy of the multivalent cation.

Conclusions

We have developed a minimal thermodynamic model to predict the extraction efficiency using acidic extractants, for example,. HDEHP. Moreover, we used the model to gain new insights in the aggregation phenomena behind extraction.

We considered only the spherical aggregates whose free energy is the sum of different contributions, that is, terms. Terms that account for the packing of the extractant chains in a highly curved interface (i.e., the film), differences in the ion concentrations and the water activities between the bulk and the core of the aggregates, the extractant head group repulsions, and the competing HDEHP dimerization work in the way of quenching the extraction. Some terms, such as the differences between an effective pK_a^° and the reservoir pH, give a distinct functionality of the extraction isotherms. When pH is low, the extraction is blocked, whereas when pH is high, the extraction is highly favorable. A dominant term called the complexation energy is always favorable (by definition), and it sets the equilibrium toward the transfer of ions from the aqueous solution to the oil phase. A small overall change of the free energy of the system upon the extraction of the ion between two phases (order of few k_BT or even less) is a consequence of the interplay of the described forces. This interplay of the forces governs the reversibility of extraction systems and indeed allows them to be referred to as a “weak self-assembly”.

The model requires a set of measurable quantities and adjusted parameters. The measurable quantities are molar volumes of ions, water molecules, extractant head groups, average extractant chain length l_chain, the effective dissociation constant pK_a^°, and the dimerization constant log K_D. We fitted the model parameters to the experimental data. The obtained parameters for dodecane with HDEHP in contact with the Eu(NO₃)₃ and HNO₃ aqueous solution system are: the standard chemical potential of HDEHP in dodecane μ_LH = 12.8 kJ mol^–1, the generalized bending constant κ* = 14 k_BT, the spontaneous packing parameter for H₂O and HNO₃p₀ = 2.6, the complexation energy for acid E_0,HNO3 = 4.2k_BT, the spontaneous packing parameter of the dissociated extractant in the film p_0,Eu³⁺ = 3.5, the complexation energy of the europium cation E_0,Eu³⁺ = 20.4k_BT per bond, and the interaction between the dissociated and undissociated extractant head groups χ_LH,L^– = 0.5k_BT. It must be noted that χ_LH,L^– can be omitted from the calculation as we have shown that the free energy associated with the lateral interactions of distinguishable head groups in the film are globally small compared to the total complexation energy (around 60k_BT). The minimum aggregation numbers found in our study correspond to 4 for the aggregate cores filled with only H₂O and HNO₃, whereas the minimum aggregation number is 6 for cores containing at least one Eu³⁺.

We used the model to study the speciation of the extractant in the solvent phase. The results show that the monomeric extractant concentration is globally small compared to the aggregated and the dimerized extractant. Both acid and metal cation concentrations in the aqueous phase exhibit a strong influence on the aggregation behavior. The low acid and the high metal concentrations in the aqueous phase favor the aggregation at the expense of the reduced dimer concentration.

The model predicts that the addition of the acid in the system diminishes the aggregation and quenches the extraction of the metal cations. For sufficiently high acid concentration, the aggregation is again induced by the pure acid extraction. Our study also predicts the Langmuir-like isotherms for the extraction dependence on the concentration of cation in the aqueous phase as well as the fact that the apparent stoichiometry is not constant. It was quantitatively shown that the apparent stoichiometry depends on the concentrations of all constituents of the system and that our model can be used to obtain the correct aggregation numbers of a given system of highly hydrophilic extractants.

The observed high complexity of the extraction system forced a change in the representation of results from traditional extraction isotherms to extraction and aggregation “maps”. Such multidimensional representation allows us to trace and quantify different regimes in both the extraction of all solutes present and the aggregation and the speciation of the extractant in the system.

The calculations show that the choice of the extractant also matters, as was reflected in the complexation energy study. A lower pH in the aqueous phase demands the extractant with higher affinity toward the target cation to balance the energy penalty for dissociation of the extractant in the media of high acidity.

Decoupling the complexity of extraction systems paves the road to a more efficient formulation design for chemical engineering. By linking the concepts of statistical thermodynamics and colloidal chemistry to chemical engineering, the derived model can be used in both hydrometallurgy and nuclear industry for metal cation recovery.

Our current work is focused on generalizing the model beyond spherical micelles (to wormlike and cylindrical reverse micelles), on the inclusion of supramolecular aspect via activity coefficients in the organic phase, and on a study of mixed two-extractant systems (since mixed systems constitute most of industrial formulations).⁷⁶

Supporting Information Available

The Supporting Information is available free of charge on the ACS Publications website at DOI: 10.1021/acs.langmuir.8b03846.

• Colloidal model of prediction of the extraction of rare earths assisted by the acidic extractant;full analytical expression for the standard chemical potential of the particular aggregate; aggregate partition function; phenomenological argument for neglecting the activity of the extractant head group in the core of the aggregate; definitions of the distribution coefficient and CAC; additional extraction and speciation of the organic phase; calculated aggregate probabilities; and flowchart of the developed software and description of the minimization procedure (ZIP)

The authors declare no competing financial interest.