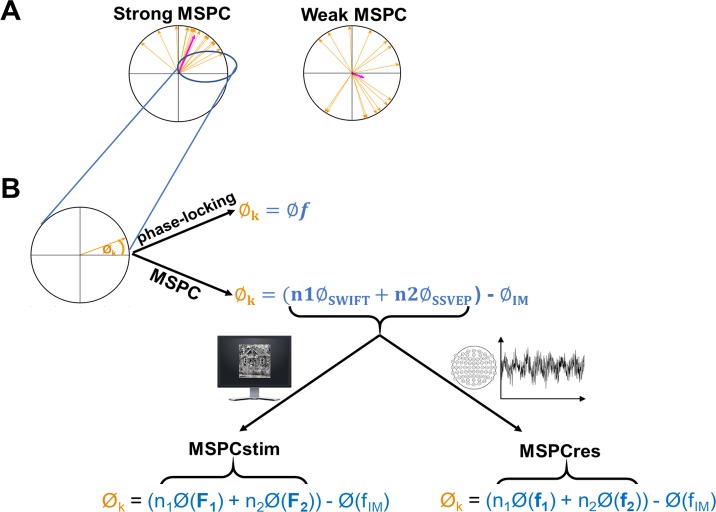
Fig 7. Multispectral phase coherence.

The method for calculating MSPC. (A) Schematic example of stronger (left) and weaker (right) phase coherence. Both the PLV and the MSPC measures examine the consistency of a given phase term across multiple epochs. This can be visualised by first converting the phase term from each epoch into a unit (length = 1) vector pointing at its phase angle. Phase coherence is then obtained by computing the average vector (the sum of all vectors divided by the number of epochs). The result is a vector whose length can vary from 0 (each vector pointing at random directions, no phase consistency across epochs) to 1 (all vectors pointing at the same direction, perfect consistency across epochs). (B) The primary difference between PLV and MSPC measures is the phase term used for each epoch. For the PLV, only the phase of one specific frequency (or frequency band) is extracted for each channel/epoch and is used as the phase term for computing phase locking. When examining consistency between distant channels, the phase term used for the PLV would be the difference (Δφ) between the phases extracted from the different channels. In contrast, the phase term used for the MSPC calculations here is based on the difference (Δφ) between the phase of a specific IM component and the (weighted sum of) phases of the fundamental frequencies within each channel/epoch. In other words, the MSPC can be understood as a measure of the extent to which the IM phases are driven by the phases of the fundamental frequencies. Our distinction between MSPCstim and MSPCres is reflected by the two MSPC formulas shown at the bottom of the figure. Specifically, MSPCstim defines the phases of the stimuli (the on-screen image) as the input (or ‘driving’) fundamental frequencies (left formula, upper case F1 and F2), and MSPCres defines the EEG response phases as the input fundamental frequencies (right, lower case f1 and f2). Note that the weights of the fundamental frequencies in those formulas (n₁ and n₂) are the coefficients that define the IM frequency (e.g., given F1 = 1.2 Hz and F2 = 15 Hz, the weights for the third-order IM component 2*F1 + F2 = 17.4 Hz would be n₁ = 2 and n₂ = 1). EEG, electroencephalography; IM, intermodulation; MSPCres, multispectral phase coherency (response); MSPCstim, MSPC (stimulus); PLV, phase-locking value.