Maximum value projection produces better en face OCT angiograms than mean value projection

Abstract

Optical coherence tomography angiography (OCTA) images rely on en face data projections for both qualitative and quantitative interpretation. Both maximum value and mean value projections are commonly used, and many researchers consider them essentially interchangeable approaches. On the contrary, we find that maximum value projection achieves a consistently higher signal-to-noise ratio and higher image contrast across multiple vascular layers, in both healthy eyes and for each disease examined.

1. Introduction

Optical coherence tomography angiography (OCTA) adds to the value of the structural OCT [1] by acquiring detailed images of vasculature [2–4]. OCTA has become a powerful clinical tool in the evaluation of retinal vascular disorders [5]. By using the flow of erythrocytes as intrinsic contrast, OCTA can show details of capillaries that have low inherent contrast in structural OCT images [6–9]. Compared to the traditional angiography modalities such as fluorescein or indocyanine-green-based angiography, OCTA is non-invasive, fast, convenient, and mitigates risks related to dye injection [10–12].

Another significant advantage of OCTA over these modalities is its three-dimensional nature. With segmentation, volume scans can reveal details of multiple layers of the retinal and choroidal vasculatures, identifying key features of major eye diseases such as diabetic retinopathy and age-related macular degeneration [13–20]. En face angiograms offer the most intuitive way of evaluating such data. They present images that are analogous to traditional angiograms, while the segmented slabs show previously unseen details of individual capillary plexuses, which are thin laminar structures with little overlap. While shadowgraphic projection artifacts can affect the slabs in the deeper layers, algorithms that resolve these artifacts have been developed to produce useful en face images for interpretation and quantification [21]. And more complex computational approaches to understand OCTA data based on, for example, machine learning often appropriate en face images as primary data [22–24].

The production of an en face image is, by necessity and by construction, a reduction (i.e. a projection) in the dimensionality of the OCTA data set (in this case, from 3 to 2 dimensions). The quality of the resultant image determines the quality of any subsequent analysis. Several innovations have improved the OCTA image quality, such as bulk motion correction [25,26] and artifact suppression [21]. The frontier of OCTA research utilizes such algorithms to reduce artifacts, but more basic decisions about image processing can profoundly influence OCTA image quality. One such example is the method used to construct the en face representation. Currently, both maximum and mean value projections are widely used [25,27]. Here, we quantitatively compare the projection schemas, and show that the maximum value projection produces better en face representations of several anatomical slabs and retinal pathologies.

2. Materials and methods

2.1 Study population

We investigated three populations, each with nine or ten participants recruited from the Casey Eye Institute at the Oregon Health & Science University (OHSU). Forty-six OCTA scans (2 scans for each eye of 8 individuals and 3 scans of each for 2) from healthy eyes, 27 scans from diabetic retinopathy eyes (from 9 individuals, 1-2 scans/eye) and 9 scans from eyes with choroidal neovascularization were evaluated (9 individuals, 1 scan/eye). The protocol was approved by the Institutional Review Board/Ethics Committee of OHSU and the research adhered to the tenants of the Declaration of Helsinki.

2.2 Data acquisition

3x3 mm macular scans were acquired with a 70-kHz, 840-nm wavelength spectral-domain OCT system (Avanti RTVue-XR, Optovue Inc.) using the AngioVue version 2016.2.0.35 software. In the fast transverse scanning direction, 304 A-scans were sampled to form a B-scan and two repeated B-scans were acquired at each lateral location. A total of 304 locations were scanned in the slow transverse direction. Axial resolution in AngioVue is 5 µm but digital pixel sampling is 3 µm. Structural OCT data was obtained by averaging the two repeated B-scans at each location and OCTA data was generated by the split-spectrum amplitude-decorrelation (SSADA) algorithm [6,28]. In order to remove microsaccadic artifacts and improve the signal-to-noise ratio of images, two sets of volumetric data were acquired at orthogonal scanning directions, registered and merged by motion correction technology (MCT). The projection-resolved OCTA algorithm was applied to remove projection artifacts [21].

2.3 Image processing and analysis

We investigated the merits of two en face projection techniques, mean value and maximum value, by performing the projections on slabs that were segmented into the superficial vascular complex (SVC), intermediate capillary plexus (ICP), and deep capillary plexus (DCP) using a previously described bidirectional graph search algorithm [29]. Mathematically we can describe en face projection as a mapping P that carries a N–element decorrelation signal vector $\mathit{D}(x,y,\mathit{z})$ along an A-scan to a number $D(x,y)$; $P(\mathit{D})\to D$, where N is the number of voxels contained within a slab along the A-scan at $(x,y)$. Explicitly, the mean of $\mathit{D}$, $\overline{D}$, is calculated as $\overline{D}=\frac{1}{N}{\displaystyle \sum }_{i=1}^N{D}_i$, while the maximum of $\mathit{D}$ is simply the largest member $D_i$ in the set $(D_1,D_2,\cdots ,D_N)$.

As seen in Fig. 1, slabs are of differing thickness and contain different relative amounts of signal and noise. Concisely, the task for en face projection is to determine what decorrelation value $D(x,y)$ within a certain slab will lead to the most informative and interpretable en face image. While many algorithms interpret en face data, the specifics of various analytic techniques are not in general conserved, which means that the “best” metric for determining image quality may be context dependent. We therefore limited our analysis to metrics that are of broad interest and essentially agnostic with respect to analytic detail; specifically, the signal-to-noise ratio (SNR) and root-mean-square contrast (RMS contrast). We calculated both of these for en face projection images obtained by either mean or maximum value projection. The former, SNR, can be conveniently defined in OCTA as

$$\text{SNR}=\frac{{\overline{D}}_{\text{parafovea}}-{\overline{D}}_{\text{FAZ}}}{\sqrt{{{\sigma }^2}_{\text{FAZ}}}}$$

where ${\overline{D}}_{\text{parafovea}}$ and ${\overline{D}}_{\text{FAZ}}$ represent means of the decorrelation in the parafovea and foveal avascular zone (FAZ), respectively, and ${{\sigma }^2}_{\text{FAZ}}$ is the variance in decorrelation in the FAZ. Since, in healthy subjects, the FAZ is avascular ${{\sigma }^2}_{\text{FAZ}}$ serves as an excellent estimate of the background in OCTA images. In the present study we manually demarcated a region within the FAZ to serve this purpose (Fig. 3). RMS contrast is a similarly simple metric obtained by calculating the RMS value across all pixels $(x,y)$ in a region of interest A:

$$\text{RMS Contrast}=\sqrt{\frac{1}{A}\times {\displaystyle \sum }_{(x,y)\in A}{(D\left(x,y\right)-\overline{D})}^2}$$

In the present study we take as the region of interest the entire en face projection. An image may have high SNR but low RMS contrast, for instance if the signal strength is strong but within signal regions pixel values are similar; alternatively, a low SNR image with high contrast may have sharp variation between pixels, yet this variation may be due in part or totally to noise. RMS contrast and SNR are thus complimentary measures, and in conjunction they provide a versatile description of image quality.

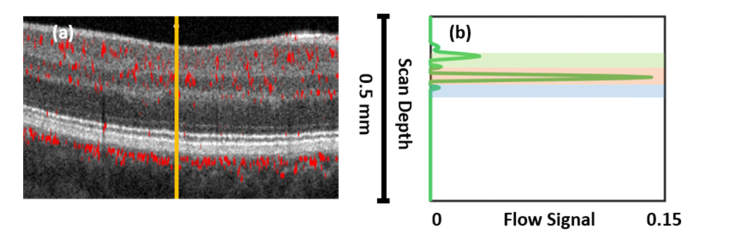
Fig. 1.

A-scan flow signal. (a) Decorrelation signal overlaid on OCT image. (b) Example A-scan decorrelation profile (green line) from the location indicated by the vertical solid orange line in (a). Shaded regions indicate the extent of the vascular layers considered in this study: green = SVC, orange = ICP, blue = DCP. For definitions of the vascular layers, see [20].

Fig. 3.

SNR and RMS contrast variation with slab thickness in the nerve fiber layer plexus. (a) 3 × 3 mm en face image of a healthy eye showing the region demarcated as FAZ for noise estimation (gray) and concentric circles defining boundaries between separate regions with varying width used to calculate SNR and RMS contrast. The series is truncated before possible edge effects can influence data in any of the measurements used to construct the averages in parts (b) and (c). The colorbar indicates decorrelation value. (b) SNR averages for concentric regions as in (a) for the 46 images examined after maximum value (red) and mean value (blue) en face projection. Error bars show standard error of the mean. Slab thickness increases monotonically with distance from the FAZ, so the leftmost point is the innermost ring, with successive points from left to right corresponding to thicker slabs and wider rings. (c) Equivalent averages for RMS contrast.

To investigate the impact of the projection technique on clinically relevant metrics, we also calculated vessel density (VD) from en face projections. VD is quantified as the percentage VD = (vascular pixels)/(total pixels) × 100. To identify vascular vs. avascular pixels we employed an Otsu threshold. The Otsu threshold is a common approach that determines a threshold value by minimizing the intraclass variance. From this threshold an effectiveness metric can be calculated. The effectiveness metric runs from 0 to 1, with 0 indicating completely ineffective segmentation (as would result from attempting segmentation on an image in which all pixels shared an identical value) and 1 indicating perfect segmentation (for instance from two totally distinguishable pixel populations, i.e. a binary image).

We conducted this research with custom software written in Matlab 2018a (Mathworks, Natick, MA).

3. Results

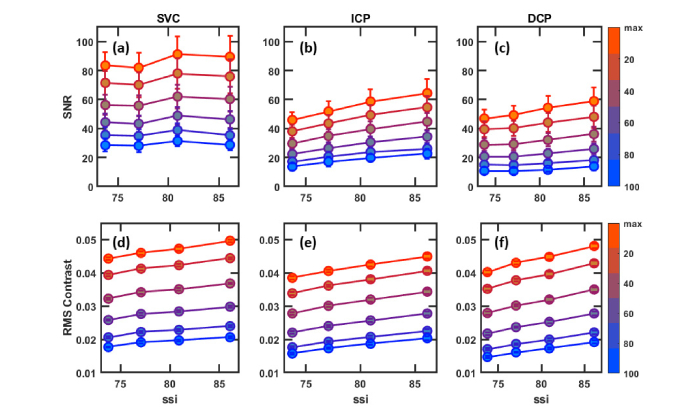
We examined a total of 46 OCTA images from healthy eyes, calculating the SNR and RMS contrast values for both maximum and mean value en face projections in 3 different retinal slabs, the SVC, ICP and DCP. To elucidate the results, we plot binned (12 points/bin, average) SNR and RMS contrast by signal strength index (SSI), a proprietary metric output by the RTVue-XR instrument. SSI is based on the average tissue reflectance amplitude of the OCT image on a logarithmic scale; it is broadly indicative of OCTA image quality and runs on a scale of 1 (poor) to 100 (excellent).

In this data set of healthy eyes maximum value projection achieves on average a better SNR and RMS contrast across every slab and SSI value. The difference between maximum value and mean value SNR and RMS contrast is greatest in the SVC and least in the ICP; not coincidentally, these are the thickest and thinnest slabs examined in Fig. 2 (mean thickness 52.9 and 31.8 µm, respectively). In thick slabs the maximum value will make up proportionally less, and in thin slabs proportionally more, of the measurements used to construct the mean value projection. We expect, then, that as slab thickness decreases the correlation between maximum and mean value projection will increase. In the limiting case where a slab is just a single pixel thick the two measurements coalesce.

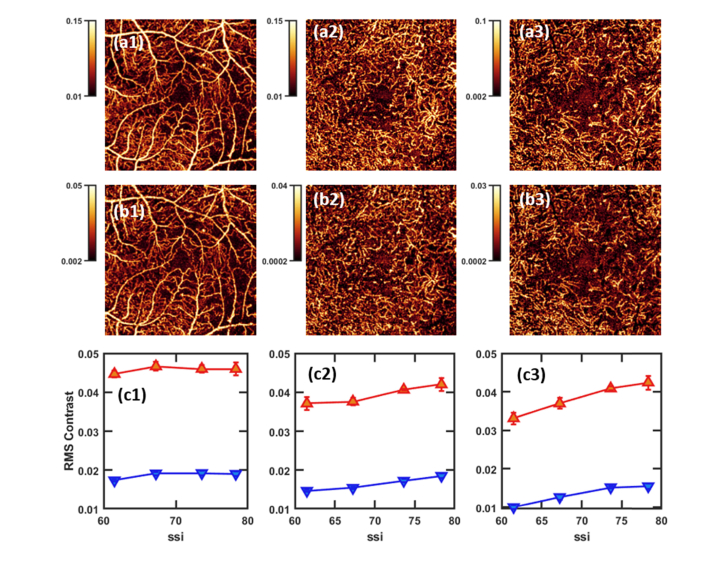
Fig. 2.

En face projections (3 × 3-mm) in healthy eyes. Colorbars indicate decorrelation value. Columns (1-3): the superficial vascular complex (SVC, 1), intermediate capillary plexus (ICP, 2), and deep capillary plexus (DCP, 3). Row a: maximum value projection, row b: mean value projection. For each set of projections, color scales were chosen such that the lowest 10th percentile of pixels will be black, and the top 10th percentile will be white in order to ensure images are similarly leveled for objective comparison. Row c: Binned maximum value (red) and mean value (blue) projection SNR for these layers, approximately 12 point/bin. Error bars show standard error of the mean. Row d: RMS contrast.

This suggests that the relative advantage of the en face projection techniques depends on the thickness of the region being projected. To investigate this hypothesis, we examined the image quality metrics across the nerve fiber layer plexus (NFLP) [30]. The NFLP is thickest in the peripheral retina but tapers near the FAZ, providing an opportunity to examine anatomically similar material with varying thickness. In Fig. 3 we show SNR and RMS contrast against slab thickness in the NFLP; the SNR and RMS contrast values were calculated for concentric regions extending increasingly further from the FAZ in 20 pixel intervals (Fig. 3(a)). Here again the maximum value projection outperforms the mean value, and we also observe the convergence of SNR and RMS contrast for the projection as the slab thins. Yet even at a relatively thin slab (4.78 pixels) maximum value projection continues to achieve superior performance. And, perhaps more importantly, each projection technique yields metrics that are correlated with slab thickness (to two significant figures, mean projection: RMS contrast correlation coefficient = 0.89, SNR correlation coefficient = 0.93; maximum value projection: RMS contrast correlation coefficient = 0.97, SNR correlation coefficient = 1.00). Since the correlation is stronger for maximum projection in both cases, we can expect that the thicker the slab, the more maximum projection will outperform mean value projection; or, similarly, we would need extremely thin slabs (i.e. somewhat less than approximately 5 pixels thick) to expect mean value projection to perform as well as maximum value projection in similar tissue.

We also examined en face projections in eyes with diabetic retinopathy (DR). DR often degrades OCTA quality, as evidenced by lower average SSI scores. Unfortunately DR affects decorrelation signal in more acute and pernicious ways than simply the reducing image quality, since disruptions like hyperreflective materials associated with exudation, such as hard exudates and suspended scattering particles in cysts, can introduce extravascular decorrelation signal into even otherwise avascular regions like the FAZ. For this reason the FAZ no longer serves as an adequate estimator for background in DR- the decorrelation signal in the FAZ can approach and indeed sometimes exceed the average decorrelation signal in the parafovea. Therefore restricting our analysis to just RMS contrast, we continue to find that maximum value projection outperforms mean value- yet by a smaller increment. Even given these diminishing returns in RMS contrast, DR is an example in which specific techniques may benefit from maximum value projection: vessel dilation can be used to accurately differentiate normal and DR eyes [31], and the higher contrast in maximum value projection is well-suited to this purpose.

One area that mean projection may be useful is in the visualization of choroidal neovascularization (CNV), since CNV develops adjacent to the choriocapillaris (CC), a region with large decorrelation signal. This means that if the boundary to the CC is not segmented precisely or accurately enough decorrelation signal may intrude into the CNV region of interest. While maximum value projection will detect and amplify this strong background, mean value projection could suppress it. CNV, then, is a clinically relevant phenomenon where mean value projection might be expected to perform relatively well. Example CNV images for each projection is shown in Fig. 5. Unfortunately, because CNV does not respect FAZ avascularity, obtaining SNR using a comparable technique to that discussed above is again impossible. We therefore limit quantitative analysis to just RMS contrast; in the 9 images analyzed maximum value projection achieves almost a three-fold better contrast (0.045 ± 0.004 vs. 0.015 ± 0.002, respectively). This quantitative result is borne out qualitatively, as CNV in the maximum value projection appears more readily identifiable by visual inspection. Maximum value representation of CNV also appears to interrupt of the CNV vasculature less.

Fig. 5.

Three examples of 3 × 3-mm en face projections of choroidal neovascularization. Colorbars indicate decorrelation value. Row a: CNV presenting in a thin layer. (a1) B-scan showing segmentation of vasculature. Purple: inner retina, yellow: CNV, red: CC. These regions are segmented by the following boundaries vitreous/internal limiting membrane (violet line), the inner nuclear layer/outer plexiform layer (yellow line), and Bruch’s membrane/retinal pigment epithelium (green line). (a2) maximum value projection, (a3) mean value projection. Row b: Another example of CNV, here in a thicker vascular layer.

The choriocapillaris (CC) itself is another intriguing target for comparison between maximum and mean value projection. From a methodological point of view, the CC is ideally suited for this study because its thickness is relatively uniform, and so the confounding effects of variable slab thickness (c.f. Fig. 3) are not operative here. But, unfortunately, as with CNV, it is difficult to obtain an accurate measurement of flow background since we again lack a physiological structure like the FAZ with which to estimate it. Once again we restrict our analysis to RMS contrast. In terms of diagnostics it is also obviously important. Several diseases present in the CC, including age-related macular degeneration [32,33] and choroideremia [34,35]. At the same time, it requires intelligent and often complex techniques to examine since it is prone to persistent imaging difficulties and artifacts due to its depth and adjacency to the retinal pigment epithelium [36–38]. However, in order for averaging to enhance signal (rather than simply suppress randomly bright pixels), we require that adjacent pixels sample the same underlying flow- a condition that probably does not pertain to capillaries in the CC, and would render this advantage to mean value projection obsolete. To investigate, we performed both projections on the data set of healthy eyes. In terms of RMS contrast mean value still lags maximum value projection (Fig. 6).

Fig. 6.

En face projection in the choriocapillaris. Colorbars indicate decorrelation value. (a) 3 × 3-mm Maximum value projection en face projection. (b) Mean value projection. For each projection, color scales were chosen such that the lowest 10% of pixels will be black, and the top 10% will be white. (c) RMS contrast. Axes in (c) are preserved from Fig. 1 row d for purposes of comparison.

Another question concerns not the relative magnitude of max and mean value projection SNR and RMS contrast but the repeatability of these metrics. To investigate we calculated the intra-visit coefficient of variation for the data set of healthy individuals and averaged the results by slab considered in the text. The results are shown in Table 1. As can be read from the table, the coefficient of variation increases with slab depth, sometimes modestly but elsewhere significantly. This is likely a manifestation of signal degradation with slab depth. While naively we may therefore have expected a low coefficient of variation for mean projection since averaging over pixel values should suppress random fluctuations, surprisingly, mean value SNR coefficient of variation increases the most with slab depth. And perhaps the more salient observation is that for both RMS contrast and SNR, maximum value projection achieves a lower coefficient of variation and therefore better repeatability.

Table 1. Coefficient of variation in healthy eyes for maximum and mean value projection by slab considered in the text.

	SNR		RMS Contrast
Layer	Max Projection	Mean Projection	Max Projection	Mean Projection
SVC	0.17	0.28	0.029	0.031
ICP	0.18	0.37	0.038	0.052
DCP	0.18	0.56	0.039	0.058

The results presented above all concern SNR and RMS contrast, which are image quality metrics. However, in OCTA we are usually most interested in diagnostic parameters such as vessel density [39,40] and vessel fractal dimension [41] or avascular area [42,43] etc., all of which can be quantified but, as noted previously, are calculated in different ways. The details of these calculations may make a far larger difference in values of the quantities obtained by a particular algorithm than the projection technique employed, and an exhaustive discussion of such quantitative features is not tractable in the context of this study. Nonetheless, we can still glean some insight as to the efficacy of both projection methods by comparing the results from sample calculations operating on en face images. We chose to examine vessel density (VD), since an estimate of VD can be obtained by simple thresholding and needn’t be an arduous computation, so we might expect the difference between the projection methods to be more apparent in the output. Here we apply an Otsu threshold to segment vascular pixels in both mean and maximum value projection in the healthy eye population from Fig. 1 for the entire en face image, excluding the FAZ. Results are reported in Table 2, as well as the effectiveness metric for Otsu thresholding. The results are statistically significant (Wilcox rank sum test p<.05 for each layer), with maximum value projection producing a higher vessel density. The choice of projection technique, at least in this context, has a noticeable impact on the results obtained from the same algorithm. It is also worth noting that, since it achieves slightly higher effectiveness metrics, we can be slightly more confident in the values reported for maximum value projection.

Table 2. Vessel density and Otsu effectiveness metric (mean ± standard deviation) in healthy eyes calculated by Otsu threshold from maximum and mean value projection.

	Vessel Density (%)		Otsu Effectiveness Metric
Layer	Max Projection	Mean Projection	Max Projection	Mean Projection
SVC	0.46 ± 0.05	0.36 ± 0.06	0.84 ± 0.02	0.83 ± 0.04
ICP	0.51 ± 0.09	0.45 ± 0.08	0.85 ± 0.04	0.84 ± 0.06
DCP	0.46 ± 0.06	0.42 ± 0.04	0.87 ± 0.03	0.87 ± 0.04

Although we so far limited our analysis to just maximum and mean value projection, it should be noted that these are only the most common techniques used to produce en face images in the literature, and not the only projection techniques possible or employed. Averaging suprathreshold voxels only or averaging the top 10the percentile, say, are also reasonable (and similar) approaches that are sometimes encountered. Actually we can consider any projection technique that averages successively larger populations of voxels as lying along a spectrum from mean projection (in which all voxels are averaged) to maximum value projection (in which just top voxel is “averaged”). In Fig. 7 we show results of projection achieved by averaging over cohorts in an A-scan in 20th percentile increments; i.e., projection in which all of voxels are included, then the top 80th percentile, then top 60th, etc. As the figure indicates, SNR and RMS contrast increase monotonically as the population of averaged voxels is reduced. This monotonic increase indicates that in terms of these metrics it is always best to include fewer members of the A-scan to form the projection. The limit of this series, of course, being to take just the maximum valued voxel.

Fig. 7.

Projection by average over different populations of voxels in healthy eyes. Colorbars on the right indicate the percentile of brightest pixels averaged over to form en face projections. Colors run from orange (maximum value projection) through purple (top 40 – 60th percentile of voxels) to blue (all voxels included, which is equivalent to mean projection). (a-c) SNR, (d-f) RMS contrast.

4. Discussion and conclusion

Parenthetically, it should be noted that even the list of projection techniques just provided is not exhaustive. Vascular pixels need not be colored according to decorrelation value after projection at all. Depth mapping is a common approach in which vascular pixels are colored according to location along an A-scan (possibly with pixel brightness still indicative of decorrelation value). In this particular instance the location of the brightest voxel along the A-scan is physically meaningful, in contrast to something akin to a “center of mass” (i.e. a weighted sum of decorrelation values) that might select a location that does not correspond to any real feature in the slab. Depth mapping then is best performed as a sort of pseudo-maximum value projection, in which the location of the maximum decorrelation voxel- rather than its value- is used to color the image. Of course pixels can convey more information that even just depth or decorrelation value, but other such pixel encodings are contextual and difficult to address in a systematic fashion.

Projections that select the value of a pixel from an operation over the voxel values are amenable to a general comparison, though. The en face OCTA image quality in terms of SNR and RMS contrast is clearly superior with maximum value projection across the tissue slabs and the disease states examined. Since both of these metrics are important for most if not all image analysis tasks, the maximum value en face projection should be used in absence of competing concerns.

Yet SNR and RMS contrast are just two quantitative metrics out of many that can and are used to characterize images. And, furthermore, as noted above, we are ultimately more interested in diagnostic parameters such as vessel density. Quantifying how the choice of projection techniques affects any specific calculation is beyond the scope of this report, but our results for vessel density give some indication that maximum value projection is also producing images in which we can be slightly more confident of further quantification. Examining just this single metric is suggestive but far from conclusive. We can, however, still take note of several qualitative features that may be important for image analysis. Qualitative features also usually lend themselves to maximum value projection. For instance, as indicated by the higher RMS contrast value captured by maximum value projection, capillaries are more easily demarcated from surrounding tissue- a considerable advantage for maximum value projection. Furthermore, capillaries appear to have their full length interrupted less by apparent noise fluctuations, indicative of a more accurate rendering of vasculature. And, finally, even when maximum value projection does incorporate noise in avascular regions into the flow signal, this noise is in general still easily discernable from the true flow signal (c.f. noisy pixels in the FAZ, Fig. 2 and 4).

Fig. 4.

En face projection (3 × 3 mm) in eyes with diabetic retinopathy (DR). Colorbars indicate decorrelation value. Column 1: SVC, column 2: ICP, column 3: DCP. Row a: maximum value projection, row b: mean value projection. For each set of projections, color scales were chosen such that the lowest 10th percentile of pixels will be black, and the top 10th percentile will be white. Row c: Binned maximum value (red) and mean value (blue) projection RMS contrast, approximately 7 data points/bin. Error bars show standard error of the mean.

Such qualitative concerns cannot be conclusively addressed in absence of concrete metrics to interrogate. One question is whether there exists a regime in which mean value projection may be useful or even outperform maximum value projection. Actually, we know that in individual images mean value projection can achieve superior SNR; it is only after averaging over populations that maximum value projection emerges a clear winner. But such pathological cases where the mean value projection obtains better SNR are typically low quality images anyway. From a logical standpoint, one should only be tempted by mean value projection in cases where most, if not all, of the A-scan is sampling just signal in the region of interest- else, using the mean projection only deteriorates signal quality by conflating it with measurements of noise. Alternatively, if the region of interest includes significant background (for instance when the vasculature is difficult to segment precisely) OCTA image quality will not be jeopardized by intrusions from randomly large decorrelation signal. Both of these conditions can pertain in CNV cases, were vasculature can be dense and background sampling of the CC (which abuts the CNV region of interest) can be problematic. And the CC itself may be an even better example- signal is plentiful and the anatomical layer is not thick. Still, at least in terms of RMS contrast, mean value projection underperforms maximum value projection even for imaging CNV or the CC, and, furthermore, features in both are just as easily discernable with maximum value projection. Actually, visual inspection reveals little intelligible variation between maximum and mean projection in the CC. In absence of a concrete qualitative difference between the approaches, the advantage of maximum projection in terms of RMS contrast offers a means to decide between otherwise seemingly equivalent choices. Ultimately, our results indicate that ideal conditions for mean projection do not pertain frequently enough in OCTA imaging to warrant much consideration, and even when they do, they do not render an obviously superior OCTA image.

Our investigation used the decorrelation signal obtained from the SSADA algorithm to construct en face angiograms, but SSADA is of course not the only OCTA algorithm available. A natural question is whether our results are transferrable to other OCTA images constructed using different algorithms (for instance optical microangiography, OMAG [7]). Although we did not investigate these alternative algorithms directly, the underlying logic that supports our conclusions is unaltered, and so we expect that maximum value projection should perform better in general, independent of the specific OCTA algorithm. It would be interesting to test this hypothesis in future work.

Since so many OCTA algorithms and diagnostic measures are concerned in the end with the vasculature it is paramount in most cases to construct the representation that can most readily distinguish between flow and non-flow pixels. SNR and RMS contrast are both excellent metrics to characterize this goal, and both indicate that maximum intensity projection is simply best suited to this task.

Funding

National Institutes of Health (R01 EY027833, R01 EY023285, DP3 DK104397, R01 EY024544, P30 EY010572); unrestricted departmental funding grant and William & Mary Greve Special Scholar Award from Research to Prevent Blindness.

Disclosures

Oregon Health & Science University (OHSU), David Huang, and Yali Jia have a significant financial interest in Optovue, Inc. These potential conflicts of interest have been reviewed and managed by OHSU.