Markerless high-frequency prospective motion correction for neuroanatomical MRI

Abstract

Purpose:

To integrate markerless head motion tracking with prospectively-corrected neuroanatomical MRI sequences and to investigate high-frequency motion correction during imaging echo-trains.

Methods:

A commercial 3D surface tracking system, which estimates head motion by registering point cloud reconstructions of the face, was used to adapt the imaging field-of-view (FOV) based on head movement during MPRAGE and T2-SPACE (3D variable-flip-angle TSE) sequences. The FOV position and orientation were updated every 6 lines of k-space (<50 ms) to enable “within-echo-train” prospective motion correction (PMC). Comparisons were made with scans using “before-echo-train” PMC where the FOV was only updated once per TR, before the start of each echo-train (ET). Continuous motion experiments with phantoms and in vivo were used to compare these high- and low-frequency correction strategies. MPRAGE images were processed with FreeSurfer to compare estimates of brain structure volumes and cortical thickness in scans with different PMC.

Results:

The median absolute pose differences between markerless tracking and MR image registration were 0.07/0.26/0.15 mm for x/y/z translation and 0.06/0.02/0.12° for rotation about x/y/z. PMC with markerless tracking substantially reduced motion artefacts. The continuous motion experiments showed that within-ET PMC, which minimises FOV encoding errors during echo-trains that last over 1 sec, reduces artefacts compared to before-ET PMC. T2-SPACE was found to be more sensitive to motion during ETs than MPRAGE. FreeSurfer morphometry estimates from within-ET PMC MPRAGE images were the most accurate.

Conclusions:

Markerless head tracking can be used for PMC and high-frequency within-echo-train PMC can reduce sensitivity to motion during long imaging echo-trains.

Introduction

Patient motion during magnetic resonance imaging (MRI) of the brain is widely recognised as a major problem in both clinical practice and neuroscience research. In clinical MRI, consequences of motion artefacts include reduced diagnostic image quality, wasted time and money for repeat scanning, and need for sedation or anesthesia in extreme cases. Andre et al. found that 16.4% of the clinical MRI scans they considered had degraded image quality that impaired diagnosis or rendered it uncertain, and furthermore estimated that the costs associated with motion are approximately $115,000 per scanner, per year (1). In neuroimaging studies, motion artefacts bias the results (2–6), particularly when comparing across groups that moved differentially during scanning. These group-wise differences in motion are common in neuroimaging studies, because the level of patient motion has been shown to vary with age, sex, and clinical status (7,8), and to be correlated with several behavioural, demographic, and physiological measures (9). High-resolution 3D-encoded scans for neuroanatomical MRI, which last on the order of minutes for a single brain volume, are particularly susceptible to complicated motion artefacts. Studies have shown that motion during such scans introduces bias and increases the variance in brain morphometry (5,10), but also that the errors can be reduced with real-time or prospective motion correction (6).

Prospective motion correction (PMC) for neuroimaging is generally implemented by estimating rigid-body head motion and subsequently adapting the field-of-view (FOV) in real-time to track the head position. There have been several successful demonstrations of this approach (11–18). Common motion measurement techniques fall into two broad classes that use either: 1) MR scanner navigators alone (12,15–17,19–22), which can typically provide low-frequency estimates every few seconds during sequence dead time; or 2) additional external equipment (11,13,14,18,23,24), where a marker (optical or MR-based) is attached to (or stamped on) the head, and motion can be tracked with high-frame rate independently of the sequence. The first approach is attractive because it does not require use of a skin-affixed marker, bite-bar or head-set, which can be both prohibitive in clinical settings and an imperfect measurement of brain motion when the marker moves relative to the brain (e.g., a marker on the forehead will move during frowning (25)). However, strategies using low-frequency motion estimates, e.g. once per ~3 s repetition time (TR), cannot correct for motion occurring during data acquisition blocks (echo-trains within a single TR), and are therefore reliant on reacquisition of TRs with substantial motion (15,17,26). In contrast, independent tracking systems can estimate motion with ~2 orders of magnitude higher temporal resolution, in turn enabling high-frequency corrections. Applying these corrections during diffusion encoding and arterial spin labelling modules (27,28) has shown benefits over slower navigator corrections. A preliminary account has also shown benefits of high-frequency correction during T2-SPACE echo-trains (29).

This study demonstrates PMC with a novel markerless method for high-frequency measurement of head motion (30) and investigates the effects of rapid motion correction during imaging echo-trains. A commercial markerless head motion tracking system (TracInnovations, Ballerup, Denmark) was integrated with a framework for PMC. The “Tracoline” system reconstructs 3D “point cloud” models of the face and registers them to a reference point cloud to estimate head movement. The structured light technique for measuring head motion (31,32) can be used for patient motion monitoring as well as retrospective or prospective correction of the acquired data. The system was first introduced for motion correction applications in positron emission tomography (33) and has since been adapted for use in MRI scanners (30), with PMC demonstrated in 3D FLASH (34). Other markerless motion measurement approaches (that do not use MR navigators) include a stereo camera system, which detects features from a stamp applied to the patient’s forehead to retrospectively correct MRI data (35), and targeted optimisation to estimate motion for retrospective correction of 2D RARE images (36).

In this study, markerless motion measurement (30–34) was integrated with prospectively-corrected T1-weighted MPRAGE (37) and T2-weighted SPACE (3D variable-flip-angle TSE) (38–40) sequences, expanding on a recent preliminary account (41). PMC performance was first tested with in vivo experiments during discrete, step-wise motion patterns, which have been shown to be largely correctable with once-per-TR PMC using MR navigators. To investigate the high-frequency tracking ability, continuous motion experiments were performed with phantoms and in vivo, focusing specifically on motion during the relatively long MPRAGE and T2-SPACE echo-trains, which last over 1 second and have minimal dead-time for MR-based navigation. Motion during echo-trains was quantified retrospectively by measuring the discrepancy between the “true”, required FOV position versus the FOV position that was prospectively encoded. The high-frequency motion measurement capability enabled updates to the FOV encoding within the echo-trains and comparisons of FOV discrepancy and image quality were made with scans where the FOV was only updated before the echo-train (once per TR). Finally, brain morphometry metrics derived from the prospectively-corrected MPRAGE images were compared with reference metrics from scans without intentional motion.

Methods

Markerless head motion measurement

The MRI-compatible Tracoline TCL3.01 markerless tracking system with TracSuite software version 2.15 (TracInnovations, Ballerup, Denmark) was used to estimate head motion (30,33). The vision probe was mounted on a detachable arm on the scanner table (see Fig. 1a). A 64-channel head coil was used for all experiments and the vision probe was positioned to allow sufficient visibility of the subject’s face through the coil opening. The Tracoline system reconstructs point cloud models of the subject’s face by projecting invisible near-infra-red structured light and recording the images in stereo. The light source and the camera are housed in a Faraday cage at the back of the scanner (see Fig. 1b). They are connected by optical fibres to the vision probe, which does not contain any electronic or magnetic components. A 3D point cloud reconstruction from a typical view of the face is shown in Fig. 1d. Head motion is estimated within the Tracoline software by defining a reference point cloud (see Fig. 1e) to which subsequent point clouds are registered. Examples of point cloud reconstructions of ginger vegetable and pineapple used for phantom experiments used are shown in Figs. 1f and 1g. The reconstructed point clouds and motion parameters were displayed in real-time on a screen in the console room for passive motion monitoring and to ensure low levels of motion during in vivo camera to scanner coordinate calibration scans (see below).

Figure 1:

(a) Camera set-up showing the camera mounted on the detachable arm over the 64-channel head coil from the front of the scanner and (b) from the back. (c) Camera to scanner coordinate calibration procedure showing the surface model of the subject’s head generated from an MPRAGE scan (blue) and the reference point cloud (gray; eye regions cropped) after the iterative closest point search. The resulting matrix transformation was used to convert motion estimates to scanner coordinates from camera coordinates during prospectively corrected scans. (d) A representative 3D point cloud reconstruction of a subject’s face viewed through the opening of the 64-channel head coil. (e) During motion tracking, point cloud reconstructions were registered to the green reference point cloud to provide motion estimates. Note that the coil is visible to the left of the face but it is not included in the green reference and therefore does not influence motion estimation. Examples of point cloud reconstructions during (f) ginger and (g) pineapple phantom experiments.

The system generates approximately 30 motion estimates per second using default settings. However, the temporal resolution varies because every 10th estimate, a calibration for the structured light procedure takes place. A group of 9 pose (position and orientation) estimates is provided with regular 25 ms intervals, followed by a 100 ms interval (while a calibration of the structured light takes place), before the next group of 9 estimates with 25 ms intervals begins, and so on. Furthermore, a pose estimate is occasionally skipped because the registration did not converge before the acquisition of the next point cloud, which occurs in less than <1% of the point clouds in our data.

The eye regions of the reference point cloud can be cropped to minimise any head motion estimates caused by eye movement (see Discussion). The eye regions were cropped in all in vivo scans, except for the experiments with subject 2.

Camera to scanner coordinate calibration

A calibration step is required to generate motion estimates in scanner coordinates for prospective (or retrospective) correction. Positioning the vision probe on the arm allows variation in camera placement, primarily in the through-bore (z) direction, and therefore coordinate calibration was required once at the start of each experiment. The transformation between camera and scanner coordinates was calculated within the Tracoline software using a surface reconstruction of a phantom or the subject’s face derived from a structural MR scan and a corresponding reference point cloud. The software uses an iterative closest point algorithm to obtain the transformation matrix that aligns the reference point cloud and the surface of the calibration scan (33), as shown in Fig. 1c (where have the eye regions have been cropped from the point cloud).

Two different configurations of the calibration procedure were used. The phantom experiments and scans with subjects 1 and 4 were pre-calibrated with a phantom using a 1 mm isotropic resolution (256×80.1×176 mm³ FOV, 650 Hz/px bandwidth) multiecho MPRAGE scan lasting 2:19 min. A ginger vegetable phantom (which has MR-visible signal close to its surface) was used for the pre-calibration and the camera was not moved before the PMC scans. A full FOV (256×256×176 mm³) MPRAGE scan lasting 6:09 min was used for the calibration scan in two of the in vivo experiments (subject 2 and 3). The high bandwidth of 650 Hz/px was used to minimise distortion and chemical shift of fat close to the skin and echoes were averaged to recover SNR (42). Although the level of motion could be monitored, this lengthy calibration scan is not practical and in the Discussion section we discuss avenues for future improvement. After this calibration step, motion information in scanner coordinates could be requested by prospectively corrected sequences via a network connection.

Prospectively-corrected sequences

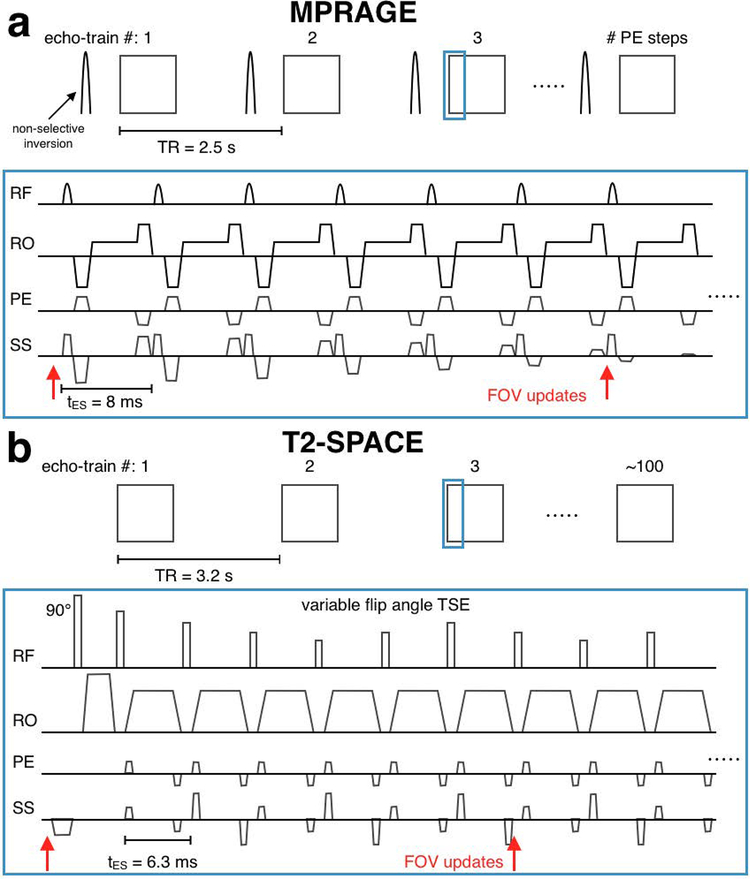
3D-encoded MPRAGE and T2-SPACE (3D variable-flip-angle TSE) sequences were modified to apply transformations to the imaging FOV using motion estimates from the Tracoline system. The FOV was updated before the start of each echo-train, and every 6 lines of k-space thereafter until the end of each echo-train (see sequence diagrams in Fig. 2). This corresponds to 30 and 32 updates per echo-train, and update intervals of 48 ms and 37.8 ms in the MPRAGE and T2-SPACE scans, respectively. The sequence instructions were written 15 ms in advance of their execution. In the experiments below, the median “age” (per scan) of pose estimates used to update the FOV ranged from 60–110 ms (see the time between red circles [point cloud acquisitions] and steps in the green line [FOV updates] in Fig. 8b).

Figure 2:

Sequence diagrams for prospectively-corrected MPRAGE (a) and T2-SPACE (b). In scans using within-ET PMC the FOV position and orientation were updated every 6 lines of k-space. In scans with before-ET PMC, only the update before the echo-train was applied (only the first red arrow).

Figure 8:

(a) Plots of x translation (one of the six rigid-body FOV parameters) during the 4 cycle/min MPRAGE in-vivo continuous motion experiments with subject 3. The top row shows the full 1-minute period and the lower row shows a zoomed section. The difference between the encoded (green line) and “true” FOV parameter (blue line) is the encoding error at each readout. The pink area represents this FOV discrepancy. For example, in before-ET PMC acquisitions, this discrepancy increases with motion during the ET. (b) Zoomed inset of the within-ET plot. The red circles represent the acquisition times of infra-red images used to generate point clouds and, ultimately, the FOV positions used for sequence updates. Thus the time delay between a red circle and the corresponding discontinuity in the green line represents the total correction latency. (c) Bar chart showing the RMS PMC discrepancy (a measure of average voxel displacement calculated using Eq. 2 from all six FOV parameters, all readouts, and all ETs in the scan) in pink, which is related to the pink areas in panels b and c. The RMS ET discrepancy is shown in blue. The RMS displacement of the point cloud centroid from the start of the scan is shown in yellow.

Data were acquired on a 3T Prisma scanner with a 64-channel head coil (Siemens Healthineers, Erlangen, Germany). 3D-encoded MPRAGE and T2-SPACE protocols with FOV=256×256×176 mm³, matrix=256×256×176, with 1 mm isotropic resolution, sagittal slice (k_z) encoding, in-plane GRAPPA R=2 were acquired. The 6:09 min MPRAGE scan had the following parameters: TR=2500 ms; TE=3.3 ms; TI=1070 ms; bandwidth=240 Hz/px; echo spacing=8 ms; ET duration = 1408 ms; turbo factor=176. The 5:34 min T2-SPACE scan had the following parameters: TR=3200 ms; TE=565 ms; bandwidth=241 Hz/px; echo spacing=6.3 ms; echo-train duration=1187 ms; turbo factor= 200.

Markerless tracking accuracy

A ginger phantom was scanned in 16 positions with a 1:16 min 1 mm isotropic 3D FLASH scan with the following parameters: TR/TE = 5.3/2.3 ms, flip angle = 5°, FOV=256×256×128 mm³, bandwidth = 400 Hz/px, GRAPPA acceleration factor R=2. Markerless tracking data were also recorded. The FLASH image from the initial position was registered to the subsequent 15 positions using the mri_robust_register FreeSurfer routine (43) and the rigid body transformation parameters were compared to the markerless tracking estimates. The 15 re-positionings of the phantom from the initial position attempted to probe all six rigid body motion parameters. Temporal standard deviation of the markerless tracking was computed for a ~30 s period at each of the 16 positions.

Cross-calibration variability

To assess the variability in position estimates introduced by calibration, the calibration procedure with the 2:19 min multiecho MPRAGE was performed six times with a ginger phantom. The table was not moved but the phantom was repositioned before each of the six calibrations. The tracking accuracy data was re-used to compute the markerless tracking pose estimates for each of the six calibration matrices, and the changes relative to the first calibration were computed.

Simulation of cross-calibration errors

The tracking accuracy data was used to assess how simulated errors in the cross-calibration matrix (C) affect accuracy (in comparison to registration of MR images). Absolute changes in FOV pose were computed relative to the original calibration (the “true” calibration with zero simulated error) when each of the six rigid body parameters of C were changed by 1 to 6 mm and 0.33 to 2°. The data were summarized by taking the median over all positions tested in the accuracy experiment to find an absolute change in each FOV parameter, for a given change in C.

Motion experiments

Markerless PMC experiments were carried out to assess the effects of low-frequency (once-per-TR) correction versus high-frequency motion correction during the 1408 ms and 1187 ms imaging echo-trains of the MPRAGE and T2-SPACE scans. This involved phantom and in vivo scans during continuous motion patterns repeated in different scans with the following PMC approaches:

1. “within-ET PMC” – FOV correction before and within each echo-train – every 6 readouts/lines, as described above and in Fig. 2;

2. “before-ET PMC” – only correcting the FOV before each echo-train, i.e., once-per-TR correction;

3. “PMC off” – no prospective correction.

Discrete changes of head position were also assessed in vivo comparing within-ET PMC to PMC off. Four subjects were scanned in accordance with Institutional Review Board guidelines.

Discrete motion experiments

Subject 1 was prompted to change head position at 1 min intervals during scans with within-ET PMC, and with PMC off. Images were also acquired when there was no intentional movement (“still” scans) using within-ET PMC and PMC off. This set of four scans was performed using the prospectively-corrected MPRAGE and T2-SPACE sequences. In the scans with discrete motion, the subject started from a central head position and then, at 1 min intervals, looked left, down, right, up, and then returned to the centre, as shown in a recording of the point clouds in Supporting Information Video S1.

Continuous motion experiments

These experiments were designed to investigate the effect of motion during the imaging echo-train (ET). In the phantom experiments, a pineapple was moved continuously (rotated back and forth about the vertical “y” axis through an approximate amplitude of 8°) for 1 min using a mechanical stage operated by hand. The 1 min motion periods began approximately 2 min and 1:45 min into the MPRAGE and T2-SPACE scans, respectively. This set of three scans was repeated for two motion speeds: one complete cycle, and four complete cycles during 1 min. A reference image was also acquired without motion and without PMC.

In the in vivo experiments, three subjects were prompted to move their heads continuously in a “no” gesture (rotating about the through-bore “z” axis) for 1 min during MPRAGE and T2-SPACE scans. A simple motion pattern was chosen that could be repeated relatively easily in controlled experiments with human subjects. The 1 min motion periods began approximately 2 min and 1:30 min into the MPRAGE and T2-SPACE scans, respectively. Different speeds of continuous motion were tested with 1, 4 and 6 cycles of motion during the 1 min motion period as described in the following summary of all motion experiments:

subject 1:

• MPRAGE discrete motion: within-ET PMC and PMC off; still: within-ET PMC and PMC off

• T2-SPACE discrete motion: within-ET PMC and PMC off; still: PMC off (Supporting Information Video S1).

• T2-SPACE discrete motion: within-ET PMC and PMC off; still: within-ET PMC and PMC off.

phantom:

• MPRAGE continuous motion with 1 and 4 cycle/min: within-ET PMC, before-ET PMC and PMC off; still: within-ET PMC and PMC off.

• T2-SPACE continuous motion with 1 and 4 cycle/min: within-ET PMC, before-ET PMC and PMC off; still: PMC off.

subject 2:

• MPRAGE continuous motion with 4 cycle/min: within-ET PMC, before-ET PMC and PMC off; still: PMC off.

• T2-SPACE continuous motion with 4 cycle/min: within-ET PMC, before-ET PMC and PMC off; still: PMC off.

subject 3:

• MPRAGE continuous motion with 1, 4 and 6 cycle/min (in separate sessions): within-ET PMC, before-ET PMC and PMC off; still: PMC off and within-ET PMC (in 6 cycle/min session).

subject 4:

• T2-SPACE continuous motion with 1 and 4 cycle/min: within-ET PMC, before-ET PMC and PMC off; still: within-ET PMC and PMC off.

• MPRAGE continuous motion with 4, 6 (with smaller range of motion), and 6 cycle/min: within-ET PMC, before-ET PMC and PMC off; still: within-ET PMC and PMC off.

Post-processing and analysis

Motion quantification

The displacement of the face/head from its initial position could be quantified via the magnitudes of the vector displacement of the point cloud centroid relative to its initial position. Note that this metric also captures information about head rotation because the centroid is on the subject’s face, and the centre of rotation is usually the back of the head. The root mean square (RMS) of the centroid displacements during the scan was used as a measure of average displacement from the initial position (“point cloud centroid RMS motion” in Figure 8 and Supporting Information S8 below). For N point cloud measurements during a scan, c_i, i = 1,…,N, are the centroid displacements from its initial position and,

$$RM{S}_{centroid}=\sqrt{\sum _i^N\frac{c_i{}^2}{N}}$$ (1)

Motion and the PMC encoding errors during the echo-trains were quantified by calculating the discrepancy between the encoded FOV position at a k-space readout and an estimate of the “true” FOV position (at the time of the k-space readout) which can be calculated retrospectively from the motion logs. This discrepancy between the encoded and “true” FOV incorporates the approximate 100 ms delay associated with generating point clouds, registering them, calculating motion, the wait for the next sequence update (6 k-space readouts per update), network communication, and the 15 ms sequence instruction writing buffer (see “Prospectively corrected sequences” section above). However, the use of PMC, and its high- vs low-frequency flavour, has the most substantial impact on the encoding error. For example, before-ET PMC will correct the FOV at the start of the ET but if there is movement during the ET, the discrepancy will increase, whereas using within-ET in PMC MPRAGE and T2-SPACE will update the FOV to the latest estimate every 48 ms and 37.8 ms, respectively.

The FOV discrepancy metrics were generated for each k-space readout, r, of each echo-train, e, and then summarised over the scan in the following way. At each readout, the FOV pose can be described by a 3×3 rotation matrix, M, and a 3×1 translation vector, x. The encoded FOV is thus described by F = (M^F, x^F) and the “true” FOV by T = (M^T, x^T). The discrepancy between them at each k-space readout, r, of each echo-train, e, is given by $D_{e,r}^{PMC}=T_{e,r}{F}_{e,r}{}^{-1}$. Using the estimated translations, Δ_x, Δ_y and Δ_z and Euler angles θ_x, θ_y and θ_z of the affine transformation D_e,r an RMS motion score of the discrepancy, $d_{e,r}^{PMC}$ can be computed as defined in Jenkinson (17,44) to estimate average voxel displacement using a 64 mm radius sphere. The RMS PMC discrepancy over the R readouts in each of the E echo-trains is then given by:

$$RM{S}_{PMCdiscrepancy}=\sqrt{\sum _{e=1}^E\sum _{r=1}^R\frac{d_{e,r}^{PM{C}^2}}{ER}}$$ (2)

To compare the level of motion during ETs in different scans using different PMC, the discrepancy was calculated in the same way, but using a modified discrepancy that simulates the FOV pose B = (M^B, x^B) of a before-ET acquisition, i.e., B is updated to track the object’s pose for the first readout of every ET, but the pose is maintained for the duration of the ET. The ET discrepancy is given by $D_{e,r}^{ET}=T_{e,r}{B}_{e,1}{}^{-1}$ and the RMS ET discrepancy by:

$$RM{S}_{ETdiscrepancy}=\sqrt{\sum _{e=1}^E\sum _{r=1}^R\frac{d_{e,r}^{E{T}^2}}{ER}}$$ (3)

In summary, the RMS ET discrepancy quantifies each scan’s level of motion during ETs (in FOV pose units) and the RMS PMC discrepancy measures the FOV discrepancy, or encoding error, after accounting for the PMC method used in each scan.

Image quality quantification

Image quality was quantified relative to a still scan with PMC off. For each session, the FreeSurfer command mri_robust_template was used to calculate a median template volume and the robust rigid registration of all the images to the template (43,45). Using images registered to the template space, the normalised root mean square error (RMSE) was calculated for each image relative to the “still, PMC off” image, over 30 central axial slices.

FreeSurfer morphometry analysis

The MPRAGE images acquired with subject 3 were processed with FreeSurfer v6.0 (46,47) to compare brain morphometry results in scans with different PMC. In this subject, the four scans acquired without intentional motion were combined to provide gold standard (GS) estimates of brain structure volumes and cortical thickness. The longitudinal analysis stream was used to generate an unbiased common template space in which to compare brain structure volumes and cortical thickness estimated from scans with different motion correction (43,45,48). Initially surfaces were estimated from the robust median volume of the four “still” scans, with each scan treated as a time point. Subsequently the template space was re-calculated to include the nine “motion” scans, and then, using the robust median surface as a starting point, each of the 13 surfaces were adjusted to reflect differences between scans. This longitudinal analysis will suppress motion effects, (see, for example, the direct comparison with cross-sectional analysis in Figs. 3 and 4 of Tisdall et al. (6)) however the resulting measures are expected to be more robust to artefacts, so in this case, remaining artefactual differences between acquisitions are those that could not be compensated for with the latest analysis techniques.

Figure 3:

Results of markerless tracking (a and b) accuracy and (c) precision phantom experiment using MR image registration as a reference. A ginger phantom was scanned in 16 positions which were intended to test all 6 rigid body transformation parameters. 30 s of temporal variation at each position was used to estimate the precision.

Figure 4:

In vivo comparison of PMC off versus within-ET PMC for scans without intentional movement and scans with discrete motion (subj. 2). (a) Displacement in camera coordinates of the point cloud centroid during the MPRAGE discrete motion scans using within-ET PMC and PMC off. T2-SPACE and MPRAGE image comparisons are shown in (b) and (c), respectively.

Using the surfaces generated with the longitudinal analysis described above, the “motion” structure volumes were compared to the GS mean of the four “still” volumes. Combined left and right volumes were computed for the hippocampus, amygdala, caudate, lateral ventricles, putamen, pallidum, thalamus, and cerebral white matter. For each structure, the difference in volume from the GS normalised by the GS volume was calculated ((vol − vol_GS/vol_GS)). The standard deviation in volume of each structure was also estimated from the four “still” volumes.

The “motion” surfaces were also compared to the “still” surfaces using a general linear model (GLM) to determine whether the motion artefacts caused apparent changes in cortical thickness. First, the surfaces were smoothed within the cortex with a 7 mm FWHM kernel (49). For each “motion” scan, a GLM was used to compare the cortical thicknesses to the four “still” scans. Each of the resulting p-value maps was thresholded separately using 5% false discovery rate (FDR) correction for multiple comparisons (using the mri_fdr FreeSurfer routine).

Results

Results from the phantom tracking accuracy experiment in Figs. 3a and 3b show good correspondence between markerless tracking and registration of the MR images. The median absolute differences between estimates were 0.07 mm, 0.26 mm, 0.15 mm for translation in x, y, and z, respectively and 0.06°, 0.02°, 0.12° for rotation around the x, y, and z axes, respectively. An apparent drift in the y translation difference up to ~0.4 mm was observed during the ~1 hour experiment which requires further investigation. The temporal precision of the estimates in a phantom was found to be approximately 0.01 mm and 0.01° (Fig. 3c).

Variability of the cross-calibration matrix (C) rigid body parameters in repeated calibrations is shown in Supporting Information Fig. S1. The corresponding changes in FOV pose relative to the first calibration are shown in Supporting Information Fig. S2 demonstrating that the FOV pose can change by up to 0.14 mm and 0.06° (maximum median changes of 0.03 mm and 0.01°) with variation in calibration. Supporting Information Fig. S3a demonstrates how errors of 3 mm and 1° in C increase differences of FOV pose estimates with respect to the MR image registration estimates. Supporting Information Fig. S3b summarizes the absolute FOV pose changes from the “true” markerless estimate (median over all 15 accuracy experiment movements from the initial pose) for calibration matrix errors of 1 to 6 mm and 0.33 to 2°.

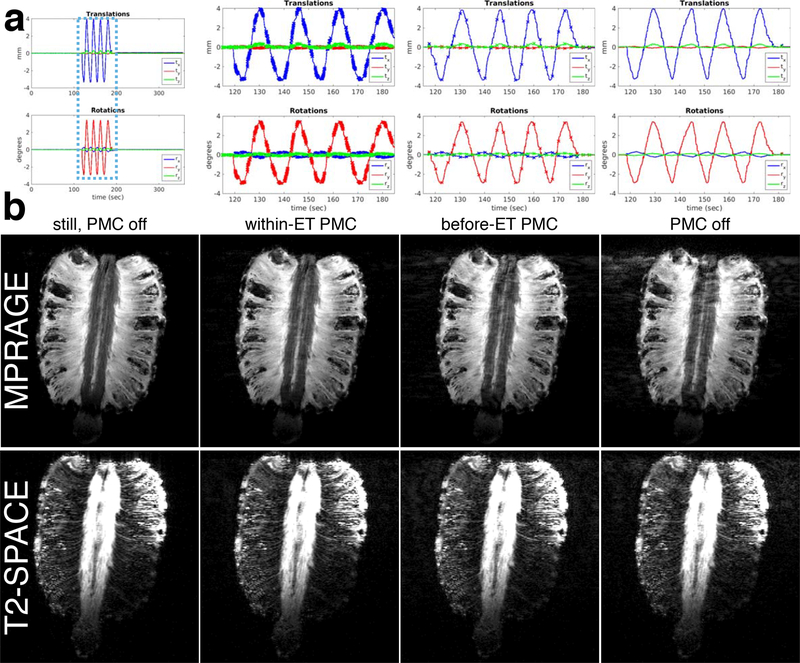
Figure 4 images and template-space RMSE values show that PMC with markerless tracking can reduce the severe artefacts caused by changing position five times during MPRAGE and T2-SPACE scans. The plots in Figs. 4a show that the centroid of the point cloud was displaced through a relatively large 15–20 mm range in these experiments. Supporting Information Video S1 shows point cloud reconstructions of the subject’s face while performing this motion paradigm in a different experiment (with the same subject). The T2-SPACE images corresponding to the motion experiment from Supporting Information Video S1 are shown in Supporting Information Fig. S4, with axial, sagittal and coronal views demonstrating the quality of correction throughout the brain.

Results of the phantom continuous 4 cycle/min motion experiments are shown in Fig. 5. Fast, within-ET correction reduced ghosting and signal loss artefacts in the MPRAGE and T2-SPACE images in comparison with the before-ET, once-per-TR correction. The “within-ET PMC” motion plots in Fig. 5a show that the required FOV position can change by ~2 mm and ~2° during an ET. This means that by the end of an ET, the image encoding can be wrong to this extent when before-ET correction is used. The corresponding results with 1 cycle/min of continuous motion in Supporting Information Fig. S5 do not demonstrate any substantial benefit of within-ET versus before-ET PMC, and both corrections improve on scans without PMC. The 1 cycle/min motion plots show that the FOV change by the end of an ET was typically less than 0.5 mm and 0.5°.

Figure 5:

Phantom comparison of PMC off, before-ET PMC, and within-ET PMC image quality during continuous motion. (a) Zoomed plots of the changes to the FOV position and orientation during the three separate MPRAGE motion scans. Crosses on the plots represent updates to the encoded FOV. (b) MPRAGE and T2-SPACE image quality of reference scans without motion and the three motions scans with different PMC.

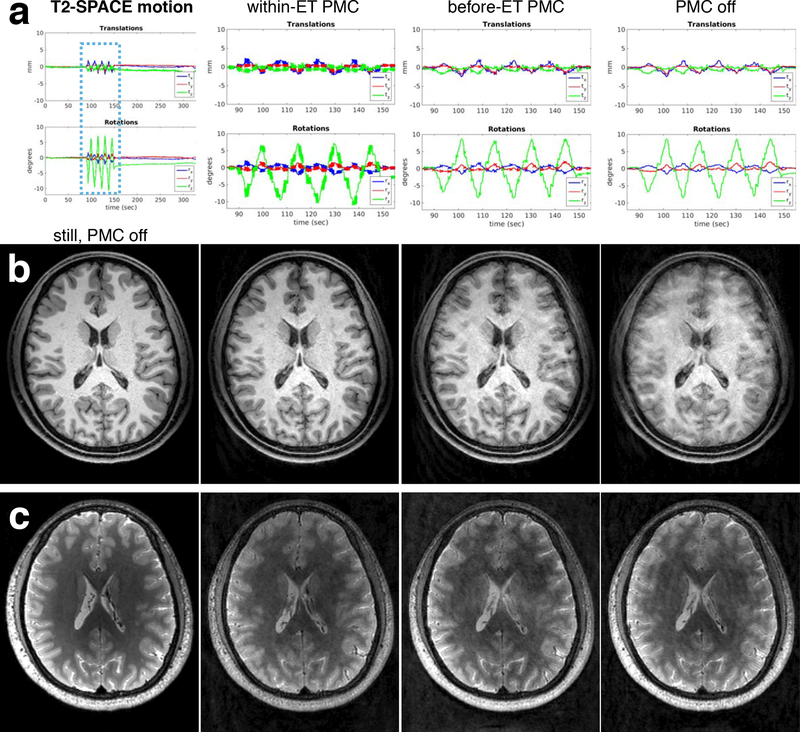
MPRAGE and T2-SPACE in vivo results are shown in Fig. 6 (full motion information in Supporting Information Fig. S6). The MPRAGE within-ET image shows comparable image quality with a no motion reference image, however, the T2-SPACE within-ET image does show residual artefacts and reduced contrast in comparison with the artefact-free reference. Within-ET images show improved detail and reduced ghosting in comparison with before-ET images, indicating that accounting for motion during ETs lasting >1 sec can improve image quality.

Figure 6:

In vivo comparison of PMC off, before-ET PMC, and within-ET PMC image quality during continuous motion (subj. 2). (a) Zoomed plots of the changes to the FOV position and orientation during the three separate T2-SPACE motion scans (similar motion during the MPRAGE scans). Crosses on the plots represent updates to the encoded FOV. (b) MPRAGE and (c) T2-SPACE image quality of a reference scan without motion and the three motions scans with different PMC.

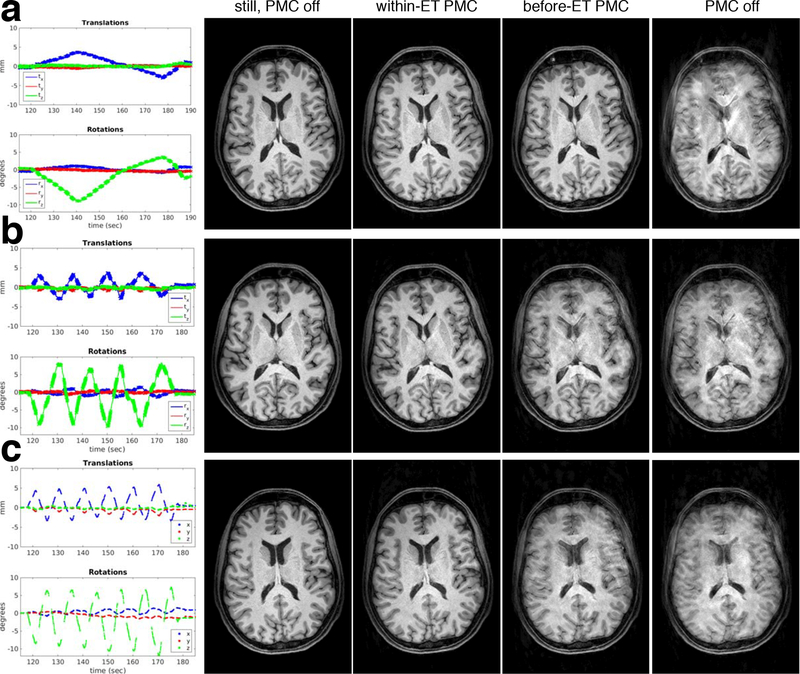
In vivo MPRAGE image quality results for varying speeds of continuous motion paradigms in the same subject are shown in Fig. 7. Motion information for all scans is provided in Supporting Information Fig. S7 – note that in the 6 cycle/min experiment with subject 3 the complete motion information was not recorded, and only the estimates sent to the scanner were stored. All motion speeds were sufficient to cause severe artefacts in the scans without PMC. Within-ET correction improved consistency between object and FOV during the relatively long image encoding ETs and recovered excellent image quality in all cases. Before-ET PMC was successful for the 1 cycle/min paradigm where there is almost no perceptible difference in image quality between the within-ET and before-ET scans. With 4 cycles of motion/min there are noticeable artefacts in the before-ET scan, which are caused by ~2 mm and ~5° discrepancies in the FOV pose between the start and finish of an ET. Similar artefacts are evident in before-ET PMC images with 6 cycle/min, when there are ~2.5 mm and ~6° pose discrepancies across ETs.

Figure 7:

In vivo comparison of PMC off, before-ET PMC, and within-ET PMC image quality during varying speeds of continuous motion (subj. 3). The motion during the within-ET PMC scan is shown in the first column for reference. Results with 1, 4 and 6 cycle/min are shown in panels (a), (b) and (c), respectively.

The discrepancies between the encoded and “true” FOV position are visualised in Fig. 8 for PMC scans using within-ET, before-ET and no correction. The plots in Fig. 8a show the x translation (one of the 6 rigid-body parameters) from the in-vivo 4 cycle/min motion experiments with subject 3. The pink areas and the pink bars in Fig. 8c show that compared with no correction, the RMS PMC discrepancy is substantially reduced by using before-ET PMC, and further reduced by using within-ET PMC. The RMS ET discrepancy for each scan (blue bar in Fig. 8c) shows that the level of motion happening during ETs was comparable in the three scans. The centroid RMS motion (yellow bar in Fig. 8c) shows that the average displacement from the start of the scan was also comparable between scans. The zoomed inset in Fig. 8b of the within ET plot shows timing delays between the red circles representing infra-red image acquisition (from the camera time stamp) and updates in the sequence FOV (steps in the green line). The FOV position shown by the green line was effectively measured at the time of a red circle and it was the most recent measurement at the time of the sequence request. Thus the delay between the red circle and the corresponding discontinuity in the green line represents the total correction latency, which includes point cloud generation, registration to the reference, and wait for a sequence request (which occurs every 6 k-space lines). Using within-ET PMC the FOV discrepancy of this translation parameter for any k-space readout can be limited to a maximum of ~0.3 mm, rather than the equivalent before-ET situation where discrepancy would increase steadily to a maximum of ~1.7 mm for the readout at the end of the ET. These values are reflected by the RMS values of the motion scores (average displacement from all six FOV parameters), all k-space readouts, and all ETs (pink bars in Fig. 8c chart) calculated using Eq. 2.

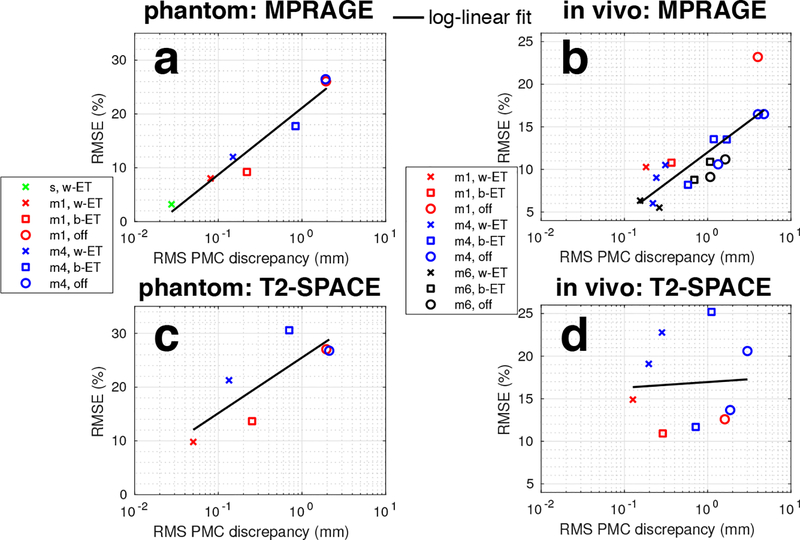
Figure 9 presents quantitative comparisons of PMC discrepancy and normalised image RMSE for all continuous motion experiments. As described above, image differences were calculated in a common space (mri_robust_template) relative to the “still, PMC off” image. The MPRAGE phantom results in Fig. 9a show that reducing RMS discrepancy with PMC improves the image quality, with larger improvement with faster motion (blue points). Similarly the in-vivo results in Fig. 9b show that low RMSE is maintained when using within-ET PMC and that there is a log-linear relationship between RMSE and RMS PMC discrepancy. Within-ET PMC has the lowest RMSE in each matched-motion comparison of within-ET PMC, before-ET PMC, and PMC off. The T2-SPACE results in Fig. 9c and 9d show that minimising RMS position discrepancy does not control image RMSE as successfully as in MPRAGE. Within-ET PMC has the lowest RMSE in the phantom experiments, but in vivo, with 4 cycle/min of continuous motion, before-ET has lower RMSE with subject 3 and no PMC has the lowest RMSE in subject 2.

Figure 9:

Comparisons of image quality measured by normalised RMSE (relative to a still scan without intentional motion) versus RMS PMC discrepancy metric and RMS centroid motion. Full version of Figure 9 with RMS ET discrepancy and RMS centroid motion graphs is available in Supporting Information Fig. S8. Data from experiments with 1, 4, and 6 cycle/min motion are shown in red, blue, and black, respectively. Note that the full motion information was not recorded for the 6 cycle/min session with subject 3 so the motion summaries could not be generated. Key for scan labels: s=still; m1=motion, 1 cycle/min; m4=motion, 4 cycle/min; m6=motion, 6 cycle/min; w-ET=within-ET PMC; b-ET=before-ET PMC; off=PMC off.

The RMS ET discrepancy and centroid motion in the second and third columns, respectively, of Supporting Information Fig. S8 (full version of Fig. 9) are provided to show that the levels of motion are comparable in each test. Furthermore, the centroid RMS motion metric in the third column is less informative about motion during ETs because it is relatively constant for different speeds, however, the RMS ET discrepancy metric increases with motion speed and is an indicator of when before-ET PMC will fail. When the RMS ET discrepancy caused by continuous motion approaches ~1 mm, before-ET PMC will not be effective as within-ET PMC.

Figure 10 shows that in MPRAGE scans with relatively high levels of continuous motion, within-ET PMC can prevent image artifacts that lead to spurious changes in cortical thickness when using before-ET or no PMC. The results are consistent with the image quality evident in Fig. 7. Unsmoothed differences from the robust median surface of all the 13 scans acquired with subject 3 are provided in Supporting Information Fig. S9. Brain structure volume estimates from MPRAGE scans with varying speeds of continuous motion (subject 3) are shown in Supporting Information Fig. S10. The MPRAGE scans using within-ET PMC produced the most accurate structure volume estimates with maximum error of 6.5%, with errors >10% for some structures in the before-ET PMC and PMC off scans.

Figure 10:

Apparent changes in subject 3’s cortical thickness estimated from MPRAGE scans acquired during 1, 4, and 6 cycle/min of continuous motion. The effects of PMC off, before-ET PMC and within-ET PMC are shown. Correction for multiple comparisons with 5% false discovery rate (FDR) was performed separately for each scan and the significance maps were thresholded accordingly.

Discussion

The presented strategy for PMC combines some of the best attributes of the previous approaches – accurate, high-frequency, sequence-independent motion estimation is possible and a marker does not need to be attached to the patient. The median absolute differences between markerless tracking and MR image registration were 0.07 mm, 0.26 mm, 0.15 mm for x, y, and z translation and 0.06°, 0.02°, 0.12° for rotation around the x, y, and z axes, respectively. Fast, markerless PMC substantially reduced artefacts during discrete and continuous motion in phantom and in vivo experiments. Importantly, it was shown that for MPRAGE imaging without any reacquisition of motion-corrupted portions of k-space, fast PMC during echo-trains can reduce artefacts during continuous motion, in comparison with scans using once-per-TR correction. This artefact reduction in the T1-weighted images translated to more reliable measurements of brain morphometry.

The acquisition of a complete echo-train lasts over 1 second in MPRAGE and T2-SPACE, during which time substantial movement can take place – over ~2 mm and ~2° in phantom experiments, and up to ~2.5 mm and ~6° in the in vivo tests. It was possible to reproduce similar continuous motion patterns with phantoms and subjects (see summaries in Supporting Information Fig. S8 and plots in Figs. 5–7 and Supporting Information Figs. S5–7) to aid comparison of scans with different PMC. This study shows that rapid correction every 48 ms during MPRAGE imaging echo-trains can improve image quality in scans with continuous motion. T2-SPACE in vivo image quality during fast motion (with ~1 mm RMS ET discrepancy – see Supporting Information Fig. S8) could not be improved to the same extent by using within-ET PMC to reduce the RMS position discrepancy during echo-trains, suggesting that the unspoiled CPMG echo-train (50–52) is more sensitive to motion than the gradient-spoiled MPRAGE readout, and that reacquisition may be necessary. A preliminary study has shown that high-frequency correction can improve T2-SPACE image quality (29) although limited information about the motion is available. One hypothesis is that phase induced by the relatively high levels of motion tested here (~1 mm RMS discrepancy per ET) during the T2-SPACE k-space readouts, leads to incomplete CPMG refocusing during the echo-train. This effect could be investigated with extended phase graph simulations (53).

Metrics were introduced to quantify motion during echo-trains in the continuous motion experiments. The RMS PMC discrepancy could be minimised using high-frequency within-ET PMC to correct for motion every 48 ms (MPRAGE) or 38 ms (T2-SPACE) during the readout, as shown in Fig. 8. As mentioned above, this was especially beneficial for MPRAGE imaging and Figs. 9a and 9b suggest a log-linear relationship between image quality and RMS PMC discrepancy. The RMS ET discrepancy, which measures the RMS movements from the beginning of each ET, allowed comparison of ET motion between scans (see Supporting Information Fig. S8). Phantom and in vivo experiments showed that low levels of motion during an ET (<0.5 mm RMS ET discrepancy) did not affect image quality when using once-per-TR correction. Increased RMS ET discrepancy (approaching ~1 mm) was predictive of increased artefact levels in before-ET PMC scans, whereas the RMS centroid movement from the initial position was less informative. Image quality is known to be sensitive to the timing of motion with respect to the k-space acquisition schedule, and this should be incorporated into sequence-specific metrics to predict artefact levels. The timing of the motion and therefore the region of k-space corruption was not varied in these experiments but this will be the subject of future work.

It is important to note that in practice, scans using before-ET PMC, such as image-space navigation with PROMO and volume navigators, have used reacquisition to reduce the artefacts caused by motion during ETs (15,17,26). The results in this study suggest that within-ET PMC reduces the number of echo-trains (or TRs) that need to be reacquired, thereby minimising additional reacquisition time. Identification and reacquisition of inconsistent data corrupted by particularly damaging motion, at crucial times in the k-space acquisition schedule, could potentially be used to further improve image quality.

This study also investigated effects of motion on brain morphometry with MPRAGE images. The motion sensitivity of morphometry is well-known (5,10) and recently it has been shown that prospective motion correction can reduce bias and variance (6); this study compared low- and high-frequency PMC. Before-ET PMC (without reacquisition) can correct for artefacts with slow continuous motion but fails with faster motion. These results suggest that using fast, within-ET PMC could provide accurate morphometry estimates without the same reliance on reacquisition as before-ET PMC.

The system’s surface matching cross-calibration technique does have potential for introducing errors, particularly in vivo. We would recommend a ~2 min (reduced FOV) calibration scan with a phantom with an additional ~2 min for the surface matching step before the subject’s scan session, and then updating the calibration matrix using the change in table position since the calibration. Maclaren et al. found that PMC was robust to errors of up to 6 mm in the z translation entry of the cross-calibration in their coil-mounted set-up (54). Supporting Information Fig. S11b demonstrates that the z translation entry of the calibration matrix can be corrected using the table position to within 0.5 mm of the measured values. Supporting Information Fig. S3 indicates that such C_z errors would manifest primarily in x translation estimates but they would be less than 0.1 mm. The calibration scan could also be avoided if the camera arm and vision probe are mounted in consistent positions (e.g. using stops) or, in a future design, on the coil (54). Similarly, if the system is kept in the scanner, then only the table position correction would be necessary.

Furthermore, data from a phantom experiment with multiple object positions (i.e. data used for accuracy quantification in Fig. 3) can be used to iteratively find a calibration that matches the MR registration transformations (11,54). This can be used with table position correction if the system is kept in the scanner or re-positioned accurately. Note that the relatively fast surface matching cross-calibration is also a potential advantage for the system, as an alternative to the time-consuming transformation matching experiment. If the system needs to be moved, e.g. for body imaging, calibration can be performed in a few minutes, or even on the subject (PMC improved image quality in the in vivo calibrated data for subjects 2 and 3).

The markerless tracking system required use of a head coil where the subject’s face was visible through the opening, which meant that the available camera mounting arm was not compatible with a tighter-fitting 32-channel coil. Future systems could optimise the optical field of view by designing the coil and the vision probe jointly. The current system is compatible with the 64- and 20-channel coils available with our Prisma 3T scanner, which are widely-used clinically and for research.

Although we have not quantified this effect, our experience using the markerless tracking system suggests that robustness of motion tracking is improved when facial features with high curvature are included in the reference point cloud, such as the nasal bridge and cheek bone. The tracking system’s software allows for customising reference point clouds, for example the eyes can be excluded from the reference to minimise errors caused by blinking. Supporting Information Video S2 shows the movement from the experiment without cropping in the reference, and similar movement was reproduced in the experiment when the eye region was cropped in the reference. The comparison of the FOV pose estimates in Supporting Information Fig. S12 suggests that the effects of opening and closing eyes may be reduced by cropping (no spikes at the start of SI Fig. S12b) although smaller spikes are still present during blinking. Supporting Information Figure S12 also shows that exaggerated frowning can cause spurious FOV pose changes of ~2 mm and ~1° (i.e., despite minimal head movement). Markers on the forehead can rotate ~10 degrees (in camera coordinates) during squinting and Singh et al. showed that with two or more markers these events can be detected and the corrupted data can be reacquired (25). Spurious changes in markerless head pose estimates, where the shape of the point cloud has changed relative to the reference point cloud, could potentially be detected and ignored, for example using the tracking “quality” metric provided by the system (plotted with pose estimates in SI Fig. S12). Note that unintentional head movement coinciding with the test conditions has not been separated, although it appears to be low, judging from Supporting Information Video S2.

Conclusions

3D surface face tracking technology enables high-frequency prospective motion correction during MRI with minimal disruption to the workflow by removing the need to attach a marker to the patient’s head. Updating the FOV position approximately every 50 ms reduced the encoding discrepancy caused by continuous motion during echo-trains that last over a second. This high-frequency motion correction was shown to improve MPRAGE image quality and brain morphometry estimates in scans acquired during continuous motion. T2-SPACE was found to be more sensitive to continuous motion. Further studies are required to determine if markerless prospective motion correction can improve diagnostic image quality and scan efficiency in clinical settings.

Supplementary Material

Supporting Information Video S1:

Time lapse video of the point clouds recorded during an in-vivo discrete motion experiment with T2-SPACE PMC. The first half of the video corresponds to the motion during the within ET PMC scan, and the second half corresponds to the scan without PMC.

Supporting Information Video S2:

Time lapse video of point clouds showing the deviations in pose estimates associated with: eyes open versus closed; blinking; frowning; looking left versus right. The video shows the experiment where the subject’s eyes were not cropped.

Supporting Information Figure S1:

The rigid body parameters from 6 repeated cross-calibrations with a phantom. The phantom was moved to different positions for each of the 6 calibrations.

Supporting Information Figure S2:

Estimation of pose variability introduced by surface matching cross-calibration. The tracking accuracy data with 15 movements from position 1 was used to compute pose estimates from six repeated calibrations. (a) The change in pose between the first calibration and the subsequent five calibrations, for all 15 movements. (b) The median pose changes over all calibrations and all movements. The boxplots show median (red line), interquartile range (blue box), the most extreme data points which aren’t outliers (black whiskers) and outliers (red crosses). A point is judged to be an outlier if it is above the upper quartile or below the lower quartile by 1.5* (interquartile range).

Supporting Information Figure S3:

Changes in pose estimates induced by cross-calibration errors. (a) Pose estimates in the accuracy experiment with 3 mm (top row) and 1° changes (bottom row) in the rigid body parameters of the cross-calibration matrix. The thick blue line shows the original data from the accuracy experiment with the measured calibration matrix (zero error). (b) Median absolute pose changes for varying calibration errors relative to the measured calibration. The dotted purple box shows the correspondence for the x translation pose estimates with 3 mm and 1° errors, and the median summaries of absolute changes over all positions.

Supporting Information Figure S4:

In vivo comparison of images acquired during the discrete motion shown in Supporting Video S1 using within ET PMC (middle column) and no PMC (right), and a still scan (left) for reference.

Supporting Information Figure S5:

Phantom comparison of PMC off, before-ET PMC, and within-ET PMC image quality during 1 cycle/min continuous motion. Zoomed plots of the changes to the FOV position and orientation during the three separate MPRAGE (a) and T2-SPACE (c) motion scans. Crosses on the plots represent updates to the encoded FOV. MPRAGE (b) and T2-SPACE (d) image quality of a reference scan without motion and the three motions scans with different PMC. Images are windowed to highlight ghosting artefacts.

Supporting Information Figure S6:

Motion information for the in vivo (a) MPRAGE and (b) T2-SPACE experiments with 4 cycle/min continuous motion with subject 2. The zoomed plots show changes to the FOV position and orientation during the motion periods of each scan. Crosses on the plots represent updates to the encoded FOV.

Supporting Information Figure S7:

Motion information for the in vivo MPRAGE experiment with 1, 4, and 6 cycle/min continuous motion with subject 3. Each row shows zoomed plots of the changes to the FOV position and orientation (pose) during the three separate motion scans for each motion speed. Crosses on the plots represent updates to the encoded FOV. Note that in the 6 cycle/min experiment (c) the complete motion information was not available due to technical problems, and only the updates sent to the scanner were stored. In scans with PMC off, updates were sent to the scanner and recorded to allow for the possibility of retrospective motion, but they were not used to update the FOV pose in real-time.

Supporting Information Figure S8:

Comparisons of image quality measured by normalised RMSE (relative to a still scan without intentional motion) versus RMS PMC discrepancy (left column), RMS ET discrepancy (middle column), and RMS centroid motion (right column). Data from experiments with 1, 4, and 6 cycle/min motion are shown in red, blue, and black, respectively. Note that the full motion information was not recorded for the 6 cycle/min session with subject 3 so the motion summaries could not be generated. Key for scan labels: s=still; m1=motion, 1 cycle/min; m4=motion, 4 cycle/min; m6=motion, 6 cycle/min; w-ET=within-ET PMC; b-ET=before-ET PMC; off=PMC off.

Supporting Information Figure S9:

Unsmoothed cortical thickness differences in mm from the robust median surface for all of the 13 scans acquired with subject 3.

Supporting Information Figure S10:

Comparison of subject 3’s brain structure volumes estimated from MPRAGE scans acquired during 1, 4, and 6 cycle/min of continuous motion. Normalised volume differences from the gold standard (mean of four “still” scans) are shown for PMC off, before-ET PMC and within-ET PMC. Key for brain structures: HP=hippocampus; AM=amygdala; CA=caudate; LV=lateral ventricles; PU=putamen; PA=pallidum; TH=thalamus; CWM=cerebral white matter.

Supporting Information Figure S11:

Assessment of table position correction for the cross-calibration matrix. (a) The rigid body parameters from 3 cross-calibration matrices when the table was moved from an initial position (1245 mm) to 2 different positions. The change in parameters is small (less than 0.3 mm and 0.1°), except for the z translation entry Cz, which is the table movement dimension. (b) Comparison of two table-corrected Cz* values to measured Cz. The Cz * values were computed by accounting for the difference in reported table position as shown in the equation on the graph. Differences are comparable with the intrinsic variability of the calibration estimated in the repeated calibration experiment (see Supporting Information Fig. S1).

Supporting Information Figure S12:

Pose deviations associated with eye movement and frowning and comparison of (a) no cropping in the reference point cloud versus (b) cropping the eyes. The eye movement or frowning test conditions are indicated at the top of the Figure. The tracking system provides a “quality” parameter, which could potentially be used to detect abrupt point cloud shape deviations from the reference point cloud. See Supporting Information Video S2 for the point clouds acquired during the experiment shown in Fig. S12a.