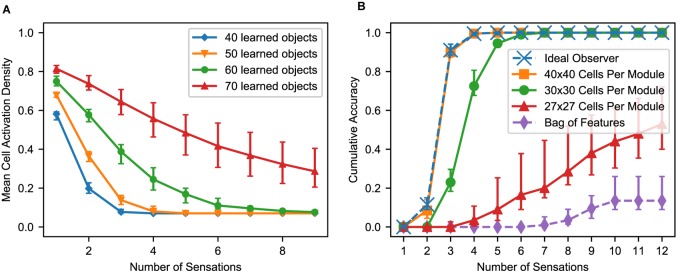
FIGURE 7.

(A) With multiple sensations, the location layer activity converges to a sparse representation. Using the same simulation from Figure 6, we show the activation density after each sensation, averaged across all objects and modules. With additional sensations, the representation becomes sparser until the object is unambiguously recognized. With more learned objects, the network takes longer to disambiguate. The activation density of the first sensation increases with the number of learned objects. If the initial activation density is low, the network converges very quickly. If it is high, convergence can take longer. (B) Comparison of this network’s performance with the ideal observer and a bag-of-features detector. Each model learned 100 objects from a unique feature pool of size 10. We show the percentage of objects that have been uniquely identified after each sensation, averaged across all objects for 10 separate trials. The ideal model compares the sequence of input features and relative locations to all learned objects while the bag-of-features model ignores relative locations. With a sufficiently large number of cells per module, the proposed neural algorithm gets similar results to the ideal computational algorithm. (A,B) In both of these charts, we repeat the experiment with 10 different sets of random objects and we plot the 5th, 50th, and 95th percentiles for each data point across trials.