Electro-Mechanical Conductance Modulation of a Nanopore Using a Removable Gate

Abstract

Ion channels form the basis of information processing in livings cells by facilitating exchange of electrical signals across and along cellular membranes. Applying the same principles to man-made systems requires development of synthetic ion channels that can alter their conductance in response to a variety of external manipulations. By combining single-molecule electrical recordings with all-atom molecular dynamics simulations, we here demonstrate a hybrid nanopore system that allows for both a stepwise change of its conductance and a non-linear current-voltage dependence. The conductance modulation is realized by using a short flexible peptide gate that carries opposite electric charge at its ends. We show that a constant transmembrane bias can position, and in a later stage remove, the peptide gate right at the most sensitive sensing region of a biological nanopore FraC, thus partially blocking its channel and producing a stepwise change in the conductance. Increasing or decreasing the bias while having the peptide gate trapped in the pore stretches or compresses the peptide within the nanopore, thus modulating its conductance in a non-linear but reproducible manner. We envision a range of applications of this removable-gate nanopore system, e.g. from an element of biological computing circuits to a test bed for probing the elasticity of intrinsically disordered proteins.

Graphical Abstract.

Lipid membranes play a crucial role in eukaryotic cells, as they separate the cell’s cytoplasm from the outside environment and from the interior of the intracellular organelles, leaving the job of transporting signals and nutrient across the membranes to membrane-embedded proteins called membrane channels.¹ One particular class of membrane channels – ion channels – facilitates transmembrane transport of specific ion species, enabling, among many other biological functions, neuronal activity^2,3 and the senses of sound, smell, sight, taste, and touch. A critical feature of an ion channel’s function is gating, i.e., the ability of an ion channel to change its conductance in response to external stimuli.

Gating of a membrane channel usually involves the opening or closing of the transmembrane pore that connects the opposite sides of a membrane with a water-filled passage that allows for ion transport across it. Diverse mechanisms have evolved to regulate the membrane channel’s conductance in response to external stimuli (Fig. 1), which include a change of the transmembrane voltage, ligand binding, pH, light, temperature, and tension.⁴ A voltage-gated ion channel opens its transmembrane pore when the transmembrane voltage exceeds a threshold value.⁵ Fig. 1a. Closing of a voltage-gated channel can proceed as a reversal of its opening or involve an additional inactivation mechanism such as, for example, in sodium channels.⁶ In a ligand-gated channel, binding of a specific chemical compound to a binding site at the channel’s surface results in a conformational transition that can either open or close the transmembrane pore, Fig. 1b. Mechanosensitive channels control the passage of ions and solutes through the cellular membrane in response to mechanical forces generated by other proteins or the membrane itself.^7,8 Fig. 1c. With the exception of a few channel types,⁹ gating of a biological membrane channel involves changes in the physical structure of the channel.¹⁰

Figure 1. Mechanisms of membrane ion channel gating.

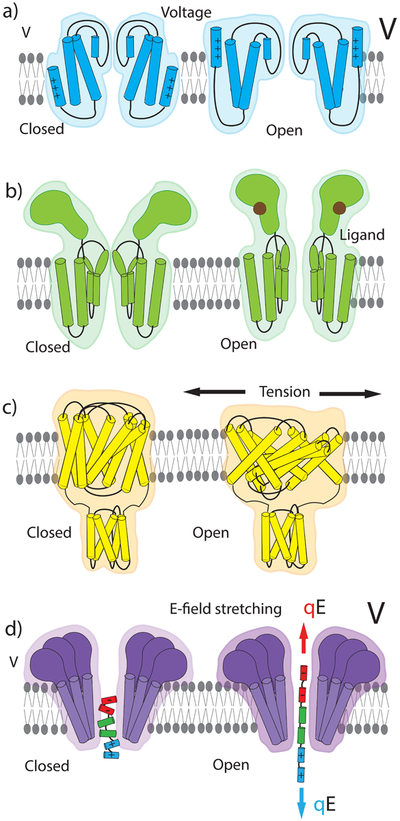
(a) Voltage-gated ion channel changes its conformation in response to an increase of the transmembrane bias. (b) Ligand-gated channel opens or closes its transmembrane pore in response to ligand binding. (c) Mechanosensitive channel opens when the membrane tension exceeds a threshold value. (d) The electromechanical gating by an insertable peptide gate investigated in this work.

Selective transport and gating of biological membrane channels has inspired biomimicry efforts.^9,11–17 Using a focused, high-energy ion or electron beam, nanopores of controlled dimensions were produced in a variety of solid-state membranes.^18,19 Because of their symmetric, uniformly charged and rigid structure, the vast majority of such nanopores exhibit a linear current-voltage dependence, which nevertheless can sensitively depend on the chemical state of the nanopore surface and thus be exploited to demonstrate pH,²⁰ light²¹ and ligand²² gating of ion conductance and rectification phenomena.²³ Nonlinear voltage-dependent phenomena can also occur in nanometer-diameter pores in ultra-thin synthetic membranes,²⁴ where quantized ion conductance ^25,26 and water-compression gating²⁷ have been reported. Nanopores in multilayer membranes offer voltage gating functionality via additional electrodes that control the electrostatic potential within the membrane²⁸ and thereby the nanopore surface charge.²⁹ Ligand³⁰ and voltage^31,32 gating was realized in synthetic nanopores made from DNA origami. Furthermore, biological pores that were initially non-gating were modified to incorporate synthetic covalently-linked gating elements, such as DNA constructs³³ and proteins.³⁴

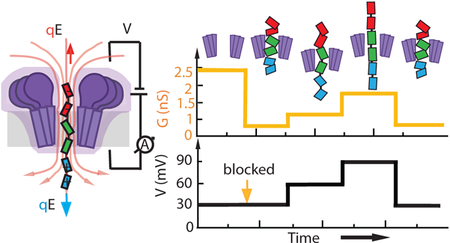
Here, we demonstrate another approach to modulation of a membrane channel’s conductance: the inclusion of a removable gate that can be the electromechanically stretched by an applied voltage, Fig. 1d. In contrast to the gating of a biological channel which typically involves a change of the channel’s conformation, or gating in a solid-state nanopore which typically involves a change of the electrostatic environment, we modulate the conductance by first trapping a bipolar molecular gate³⁵ and then alter its conformation by varying the magnitude of the transmembrane bias. Our single-molecule electrophysiology recording and all-atom molecular dynamics (MD) simulations show that stretching of the molecular dipole can alter the ionic conductance of the assembly in a controllable and reproducible way. Our work sets the stage for development of artificial nanopore systems with programmable voltage-current responses, which could, for example, be used to introduce an action potential-like response into a network of synthetic cells.³⁶

RESULTS

To demonstrate the working principle of our removable gate, we used a wild-type Fragaceatoxin C (FraC) nanopore as our model system (Fig. 2a). As revealed by its crystal structure,³⁷ FraC is a conically-shaped octameric transmembrane pore. At the trans opening of the pore, eight alpha helices form a V-shaped channel that ends in a narrow pore constriction of 1.4 nm. Because of its narrow constriction and conical shape, FraC has been successfully used for the analysis of a wide range of peptides and proteins³⁸ as well as DNA.³⁹

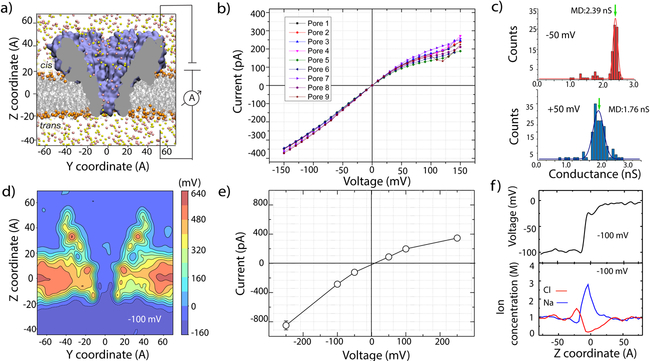
Figure 2: Ionic conductivity of the FraC nanopore.

(a) All-atom model of a FraC nanopore (blue cut-away surface) embedded in a DPhPC membrane (grey lines and orange spheres) and submerged in 1 M NaCl solution (pink and yellow spheres representing Na⁺ and Cl⁻ ions, respectively). A bias of transmembrane electric potential is applied to produce a current of ions through the FraC nanopore. (b) Experimentally measured current-voltage dependence of nine FraC nanopores. (c) Experimentally determined distribution of the FraC conductance value under a negative (top) and positive (bottom) bias of 50 mV. Green arrows denote the conductance values obtained using the MD method. (d) Electrostatic potential map of FraC obtained from MD.⁴⁰ The potential map was produced by averaging the instantaneous distributions of the electrostatic potential over a 48 ns MD trajectory obtained at a −100 mV transmembrane bias. A 2D cross section (parallel to the pore axis) of the 3D map is shown. (e) Simulated current-voltage dependence of the FraC nanopore. (f) Simulated profiles of the electric potential (top) and of the Na⁺ and Cl⁻ concentrations (bottom) along the central axis of the FraC nanopore. The data were obtained by averaging instantaneous configurations over a 48 ns MD trajectory.

Figure 2a shows our measurement set up. We first experimentally characterized the pore in its open state by measuring the current-voltage response of the channel (I-V curve) in the −120 to 120 mV range (Fig. 2b). All our measurements were performed in a buffer containing 1 M NaCl, 10 mM Tris and 1mM EDTA at pH 7.5. Our reference electrode was located in the cis compartment while the working electrode was placed in the trans compartment. Figure 2b shows I-V recordings for nine FraC nanopores, all of which feature a persistent rectifying behavior. In addition to the current-voltage dependency, we also analyzed the conductance of individual channels in an extensive set of pores (n=93). At an applied voltage of 50 mV, we observe a consistent conductance value of 1.76 ± 0.15 nS for positive bias and 2.39 ± 0.07 nS for negative bias, Fig. 2c.

Reproducing the experimental setup, we constructed an all-atom model of the FraC nanopore embedded in a lipid bilayer and solvated in 1M NaCl solution, Fig. 2a; see Methods for detailed description of the structural model and simulation protocols. The resulting model was equilibrated in a 80 ns MD simulation, reaching a stable conformation characterized by the average root mean squared deviation from the crystallographic coordinates of about 3Å, SI Fig. S1 and SI Movie 1. The all-atom model of the open-pore FraC system was then simulated under a −100 mV transmembrane bias for 48 ns, which revealed the distribution of the electrostatic potential within and around the channel, Fig. 2d. Similar to electrostatic potential maps of alpha-hemolysin⁴⁰ and MspA,⁴¹ the transmembrane voltage is found to vary sharply within the constriction of the channel.

By repeating the simulation at several values of the transmembrane voltage and recording the resulting displacement of ions, we obtained the in silico I-V curve of the FraC nanopore, Fig. 2e. SI Movie 2 illustrates the ion conductance process. The simulated I-V curve reproduced many features of the experimentally determined I-V curve, in particular the ionic current rectification experimentally observed and its dependence on the voltage magnitude. Furthermore, the simulated ionic conductance values appear to be in quantitative agreement with the experimentally determined conductance values, with 1.76 nS at +50 mV and 2.39 nS at −50 mV (Fig. 2c). The current rectification in FraC is of inverse polarity to that previously observed for large conical solid-state and polymeric nanopores.^42–45 Such an inversion of the current rectification was reported previously for nanopores with similar characteristics to FraC, i.e., a pore diameter that is comparable to the width of the electric double layer and strong ion selectivity.^46,47 Indeed, under our simulation conditions, the current through FraC nanopore was cation-selective, with Na⁺ ions carrying 55 to 75% of the total current, in broad agreement with ion selectivity established earlier for KCl.³⁹ The selective conductance produced an electro-osmotic effect: the direction and magnitude of the water flux through FraC followed the direction and magnitude of the current of Na⁺ species. The plot of the electrostatic potential along the symmetry axis of the nanopore, Fig. 2f top, exhibits a sharp drop across the FraC constriction. Interestingly, the concentration of chloride ions within the FraC constriction is reduced whereas the concentration of sodium ions is enhanced, Fig. 2f bottom. The variation of the electrostatic potential is more gradual at a reverse bias polarity (SI Figure S2), whereas the concentration profiles remain largely unchanged. The observed distributions of the ionic species within FraC are well explained by the overall negative charge of the FraC constriction.

Having established the ion conductance properties of the FraC nanopore, we experimentally characterized the effect of the electromechanical gate on the FraC conductance. Our electromechanical gate was a 30-amino acid bipolar peptide containing ten negatively charged amino acids at its N-terminus and ten positively charged amino acids at its C-terminus. A flexible linker region, consisting predominantly of glycine (G) and serine (S) residues, connected the two charged regions. The bipolar peptide gate was added to the cis compartment in concentrations of 0.3 to 0.5 μM. Upon applying a negative bias to the trans compartment, frequent and pronounced current blockades were observed at voltage biases in the −20 to −110 mV range, Fig. 3b. At a fixed bias voltage, the event rate was found to increase with the peptide concentration, whereas the dwell time remained constant (SI Fig. S3), confirming our interpretation of current blockades as being produced by the interaction of individual peptide gates with the FraC nanopore.^48,49 We suggest that the peptide traverses the pore with its positively-charged end first, but, after the negatively charged end enters the FraC vestibule, the two charged regions are pulled in opposite directions by the transmembrane bias. Together with the force exerted by the electro-osmotic flow (EOF), this creates a tug-of-war mechanism that stalls the peptide at the position where the forces on the probe balance each other. The exceptionally long translocation times (>1 s) observed at some voltages confirm this hypothesis.

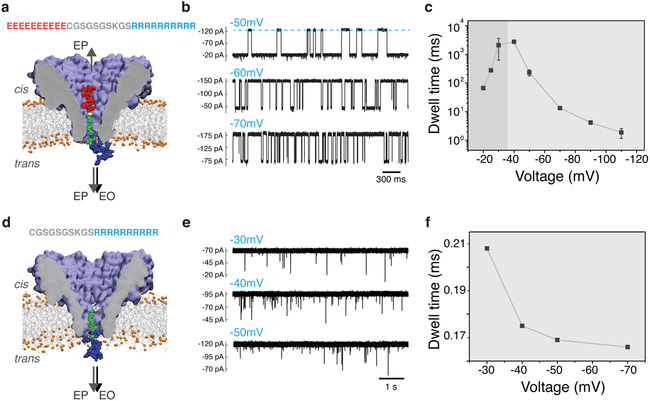
Figure 3: Experimental detection of the bipolar peptide translocation through FraC.

(a) Schematic of the peptide translocation experiment. The sequence of the bipolar peptide is listed above the molecular graphics image of the nanopore. Negative bias is applied to the trans side of the nanopore. (b) Typical current traces observed after adding 0.4 uM of bipolar peptide to the cis compartment. Transient reductions of the current indicate interactions of the individual bipolar peptides with the FraC nanopore. (c) Average duration of the current blockade (dwell time) produced by the bipolar peptide as a function of the transmembrane bias. Below approximately −40 mV, the dwell time increases with voltage indicating transient entrapment of the peptide and, likely, subsequent escape through the cis entrance of the nanopore. At voltages higher by magnitude than −40 mV, the dwell time decreases with the voltage indicating that the peptide exits the pore to the trans side. (d) Schematic representation of a control measurement performed using a truncated version of the bipolar peptide lacking the negatively charged segment (ten glutamate residues). (e) Typical current traces observed after adding 0.5 uM of the truncated peptide variant to the cis compartment. (f) Average residence time of the truncated peptide versus transmembrane bias.

The residence time of the bipolar gate in the FraC pore has a pronounced dependence on voltage, Fig. 3c, spanning the range from a few milliseconds (1.88 ms at −110 mV) up to few seconds (2.7 s at −40 mV). At low applied potentials, with a magnitude below −40 mV, the dwell time is observed to increase with voltage, while at higher voltages the dwell time decreases with voltage. This biphasic behavior of the dwell time has been previously reported by others and is typically associated with two different regimes of the analyte interaction with the nanopore.^38,50–54 The first regime, where the dwell time increases with voltage, is generally attributed to events in which the molecule exits the pore through the cis opening. The second regime, where the dwell time decreases with voltage, is generally attributed to molecules that translocate the pore and exit through the trans side. We hypothesize that in our FraC system, at higher voltages (> 40 mV by magnitude) the increased EOF exerts increasing forces to the peptide towards the trans side of the pore, thus facilitating translocations and decreasing its residence time in the pore.⁵⁵

The effect of the positive and negative charges of the peptide gate was further confirmed by carrying out nanopore translocation experiments using a modified version of the peptide gate in which the polyanionic fragment of the peptide was removed. Upon the addition of the modified peptide to the cis compartment, we observed very fast translocations, with a translocation time of the order of hundreds of microseconds. At −30 mV, for example, the average residence time of the modified peptide was 208 μs compared to 2.12 s for the bipolar gate, a difference of four orders of magnitude. These results demonstrate that both charged ends are necessary to establish trapping of the peptide gate.

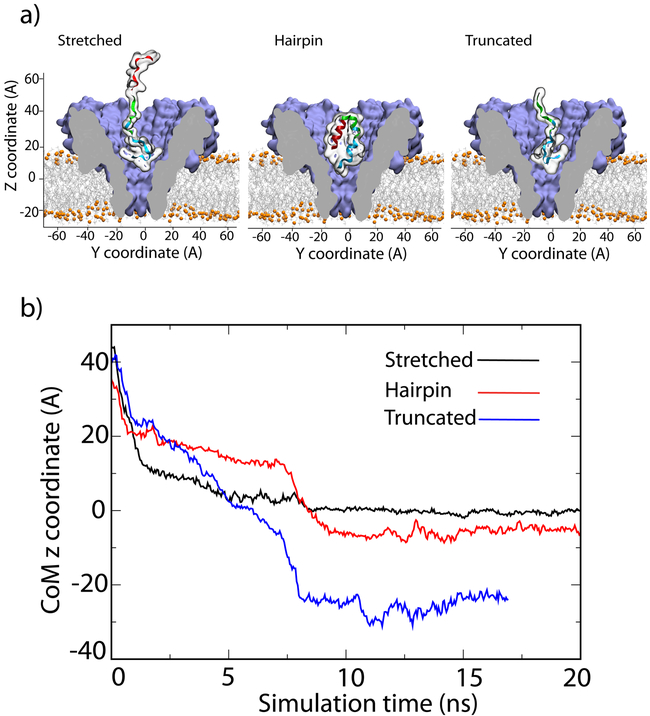
To obtain a microscopic interpretation of the peptide translocation experiment, we constructed three all-atom models of the FraC nanopore system differing by the structure and conformation of the peptide, Fig. 4a. In the first system, the bipolar peptide was placed in the FraC vestibule having its polycationic end proximal to the constriction. After initial energy minimization and 19 ns equilibration, the system was simulated under a −1.2 V bias, which produced rapid capture and transport of the polycationic tag through the FraC constriction. The translocation, however, halted after the polycataionic tag passed through the constriction, see SI Movie 3 and Fig. 4b, which plots the z-coordinate of the peptide CFSFSFSKFS segment’s center of mass (CoM) as a function of the simulation time. Fig. 5a shows a representative conformation of the trapped peptide system. A qualitatively different outcome was observed when the simulation was repeated using a version of the peptide lacking the polyanionic part: the peptide completed the translocation in 10 ns leaving the FraC constriction, SI Movie 4 and Fig. 4b. To investigate the robustness of the entrapment mechanism with regard to the initial conformation of the peptide, the peptide was simulated in 1M NaCl solution for 50 ns in the absence of the FraC nanopore. The conformation of the peptide was observed to change from an initially extended, disordered structure into an alpha-helical hairpin, held together by electrostatic interactions between the polycationic and polyanionic parts (SI Movie 5). Next, we repeated the nanopore translocation simulation starting from the full length bipolar peptide in the hairpin conformation. Similar to the outcome of the previous simulation, the polycationic part of the bipolar peptide was seen to pass through the FraC constriction, unfolding the hairpin (SI Movie 6). Interestingly, the translocation halted when the peptide reached approximately the same location within the FraC nanopore as in the simulation that initiated starting from a stretched conformation, Fig. 4b, which confirmed robustness of the trapping mechanism.

Figure 4:

MD simulation of peptide translocation through the FraC nanopore. (a) Setup of MD simulations that examined the effect of the peptide sequence and conformation on electric field-driven translocation of model peptides. Molecular graphics images illustrate initial conformations of the peptides: two conformations of the bipolar peptide (stretched, left, and forming a hairpin, middle) and one conformation of the truncated peptide (right). In each simulation, one peptide construct was placed at the cis entrance of the FraC nanopore and simulated under a transmembrane bias of −1.2 V. (b) Center of mass coordinate of the “CGSGSGSKGS” central segment of the three peptides versus simulation time. The z coordinate is defined in panel a. After about 10 ns, the bipolar peptides remain trapped within the FraC nanopore regardless of their initial conformations, whereas the truncated peptide exits the FraC pore toward the trans side.

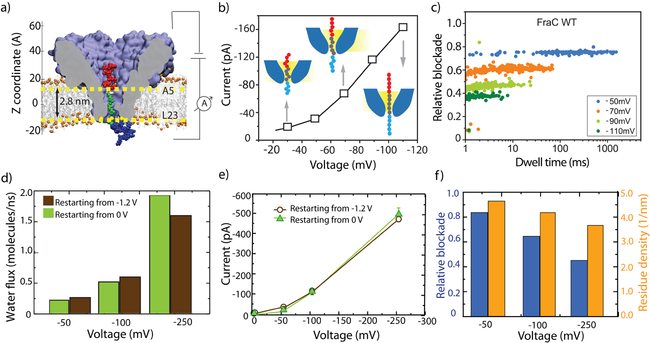
Figure 5: Effect of transmembrane bias on relative current blockade.

(a) Representative microscopic configuration observed at the end of an MD simulation where a bipolar peptide was captured and trapped by a transmembrane bias. The amino acids of the bipolar peptide are colored according to their charge: negative, positive, and neutral residues are shown in red, blue, and green, respectively. The constriction region of FraC is marked by horizontal dashed lines corresponding to average z coordinate of the eight Ala5 and eight Leu23 residues. (b) Relative blockade current, I_b/I₀, versus dwell time for bipolar peptides trapped within the FraC nanopore at several biases. (c) Average blockade current experimentally measured upon trapping of the bipolar peptides within the FraC nanopore as a function of transmembrane bias. Inset images illustrates the proposed voltage-induced stretching of the peptide trapped within the nanopore. (d) Average flux of water molecules through FraC nanopore blocked by the peptide gate. Data shown in different colors correspond to two independent simulations differing by the initial conformations of the bipolar peptides. (e) Average blockade currents measured from MD simulations of trapped bipolar peptides as a function of transmembrane bias. Data shown in black and green correspond to two independent simulations of the blockade currents differing by the initial conformations of the bipolar peptides. (f) The relation between peptide stretching and blockade current. Blue bars (left axis) show the simulated relative blockade whereas orange bars (right axis) show the peptide density within the FraC constriction.

Next, we investigated the effect of the applied bias on the ionic current blockade. Figure 5b shows the scatter plot of relative blockade vs. dwell time obtained experimentally for a range of voltages between −50 and −110 mV. The relative blockade is calculated as the current blockade (ΔI) divided by the open pore current (I). It is clear from the plot that the relative blockade decreases at increasing bias, indicating that the fraction of the pore that is blocked by the peptide gate changes depending on the applied bias. These results are confirmed by the current-voltage relation presented in Fig. 5c: a superlinear behavior is observed for this I-V curve indicating a change in resistivity of the peptide/FraC system at different voltages.

Complementing these experiments, we probed the dependence of the nanopore ionic current blockade produced by the bipolar gate on the transmembrane voltage in MD simulations. The conformations of the trapped peptide obtained at the end of the nanopore capture and translocation simulations (Fig. 4a, b) were used to initiate four independent simulations, each lasting about 150 ns, at −250, −100, and −50 and 0 mV. The final state of the 0 V run was then used to run three independent simulations at −250, −100, and −50 mV to obtain at least two independent trajectories for each bias condition. SI Figure S4 illustrates the change in the location of the peptide’s central fragment during these simulations whereas SI Movie 7 illustrates one such trajectory. While the bipolar peptide remains trapped within the nanopore, water and ions can flow through the gate. Quantitative analysis of the MD trajectories confirms our earlier conjecture about the presence of the EOF, Fig. 5d, and shows that the EOF magnitude indeed increases with the magnitude of the voltage bias, pushing the peptide, on average, toward the trans side. Figure 5e shows the simulated dependence of the blockade current on voltage: the current increases superlinearly with the voltage for both types of initial conditions, as in the experiments. The simulated relative blockade current is found to decrease with the bias, similarly to the dependence seen experimentally. By plotting the peptide residue density inside the constriction region of FraC (defined by residues Ala5 and Leu23) as a function of voltage, Fig. 5f, we find a lower peptide density under higher voltage, a manifestation of the polar gate stretching in electric field. A set of simulations carried out at a fixed conformation of the gate peptide yielded a linear I–V dependence (SI Figure S5), validating our assertion that peptide stretching is responsible for the non-linear behavior. Based on the results of simulation and experiment, we arrive at a model where higher transmembrane bias stretches the removable gate, thereby occupying less volume inside the FraC constriction, which lets more ions to pass through, i.e. the conductance is electro-mechanically modulated.

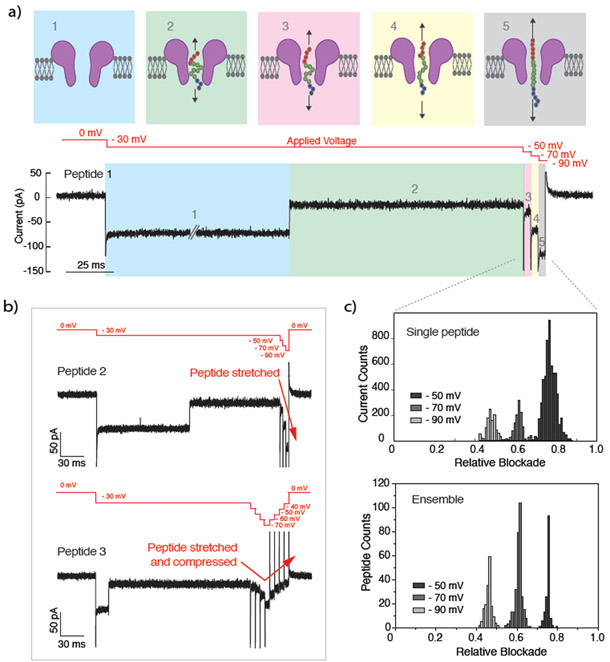
The above results confirm the working mechanism of our electromechanical gate, where the fraction of the pore occupied by the gate can be modulated as the peptide is stretched to varying degrees at different applied voltages. However, the data presented in Fig. 5b, c were obtained by averaging over hundreds of single-molecule experiments, where individual peptides were captured at a constant applied voltage. To demonstrate dynamic electromechanical modulation of the ionic current at the true single-molecule level, we trapped individual peptides, one at a time, in the FraC nanopore and subsequently modulated the conformation of the captured peptide by changing the magnitude of the applied voltage. Figure 6a shows a typical ionic current trace recorded from such measurements. First, we apply a low bias of −30 mV until a single peptide is captured by the FraC pore. Panel 1 represents the open pore current upon applying −30 mV and panel 2 shows the moment when the peptide is captured. At this voltage, the relative blockade of the peptide is 0.77 ± 0.05 indicating that a large portion of the pore current is obstructed. We subsequently apply steps of −50, −70, and −90 mV while the peptide remains trapped inside the nanopore. As expected, a current increase is observed after each voltage step, as can be observed in panels 3, 4, and 5. Interestingly, when the relative blockade is calculated for each of the voltage intervals, we find a relative blockade of 0.73 ± 0.04 for −50 mV, 0.61 ± 0.02 for −70 mV and 0.48 ± 0.02 for −90 mV. Thus, the relative blockade reduces with increasing bias for an individual molecule, indicating that the peptide is stretched further with each voltage step. As shown in the traces of Fig. 6b, a trapped peptide can also be continuously stretched (top trace), or it can be first stretched and then compressed (bottom trace). Importantly, we observed well-defined, reproducible levels of blockade currents regardless of the direction of the voltage ramp.

Figure 6: Electro-mechanical modulation of FraC conductance.

(a) Schematic of the single-peptide capture and stretching. Level 1 represents the open pore current. Level 2 represents the peptide captured at low voltages (−30 mV). Level 3, 4 and 5 represent peptide stretching at −50, −70 and −90 mV consecutively. (b) Current trace corresponding to the capture and stretching of a single peptide. The very first part of the recording shows capture of the FraC nanopore. (c) Current traces of individual peptides being stretched (top), or stretched and consequently compressed (bottom). (d) Example histogram of the current values corresponding to stretching a single peptide within FraC nanopore by −50, −70 and −90 mV voltages (top). Histogram of current blockade values obtained from multiple measurements of multiple peptides, each carried out at one of the following fixed value of the applied voltage: −50, −70, and −90 mV (bottom).

To verify the correspondence between current modulations observed at the single-molecule level and those measured previously from the ensemble measurements at constant bias conditions, we plot in Fig. 6c the histograms of the relative blockade currents obtained for the two types of experiments. The peaks of the relative blockade current are seen to occur at the same values at the same voltage bias in both single molecule and ensemble measurements. Altogether, our results prove that our electromechanical gate can be used to modulate pore conductivity both dynamically and at a true single-molecule level.

CONCLUSIONS

In this work, we combined ionic current measurements with MD simulations to demonstrate a mechanism for the modulation of a membrane channel conductance: electromechanical stretching of a removable gate. Our gate was a peptide containing a fragment of ten negative amino acids at the N-terminus and ten positive amino acids at the C-terminus. Subject to opposing electrophoretic forces pulling both ends of the peptide in different directions, the peptide is transiently stalled in the nanopore for a time interval that greatly exceeds typical peptide translocation time and can reach seconds. The magnitude of the ionic current flowing through the nanopore blocked by the removable gate was found to increase superlinearly with the magnitude of the applied bias. Our simulations determined such a peculiar conductance modulation to originate from differential stretching of the peptide under applied biases. The peptide can therefore act as a gate that modulates the pore conductance in a voltage-dependent manner. Additionally, true single-molecule experiments were performed, where an individual peptide was stalled within the pore and voltage steps were applied to gradually stretch and compress the peptide, yielding relative blockades that matched those obtained in ensemble measurements involving several hundreds of peptides.

This mechanism of channel conductance modulation could be used for several applications. For example, ion channel blockers or modulators are often used to control ion transport through channels for therapeutic purposes in diseases such as multiple sclerosis or epilepsy. A peptide gate could be modified with a recognition amino acid sequence to target a specific family of channels for therapeutic purposes. Additionally, this system could work as an interface between gene expression and ionic current, where expression (and translation) of gate peptides affects membrane potential, which may be useful for creation of regulatory circuits in synthetic biology and for a realization of natural computing.⁵⁶ The properties of the gate can obviously be fine-tuned by changing the peptide sequence. Different peptide sequences would result in different elastic response and baseline current, potentially fulfilling any range. The initial hairpin conformation of the peptide can be exploited such that a threshold bias is necessary for hairpin rupture. Finally, the long observation times offered by the dipolar peptide constructs may allow for extended examination of the central region of the peptide, which could be used for the analysis of amino acids and their post-translational modifications.

METHOD

General MD Methods.

All simulations were performed using the classical MD package NAMD,⁵⁷ periodic boundary conditions, and a 2 fs integration time step. The CHARMM36 force field⁵⁸ was used to describe proteins, dioctadecatrienoylphosphatidylcholine (DPhPC) phospholipids, TIP3P water, and ions along with the CUFIX corrections applied to improve description of charge-charge interactions⁵⁹ RATTLE⁶⁰ and SETTLE⁶¹ algorithms were applied to covalent bonds that involved hydrogen atoms in protein and water molecules, respectively. The particle mesh Ewald (PME)⁶² algorithm was adopted to evaluate the long-range electrostatic interaction over a 1 Å-spaced grid. Van der Waals interactions were evaluated using a smooth 10−12 Å cutoff. Langevin dynamics were used to maintain the temperature at 295 K. Multiple time stepping was used to calculate local interactions every time step and full electrostatics every three time steps. The Nose-Hoover Langevin piston pressure control⁶³ was used to maintain the pressure of the system at 1 atm by adjusting the system’s dimension. Langevin thermostat⁶⁴ was applied to all the heavy atoms of the system with a damping coefficient of 0.1 ps⁻¹ to maintain the system temperature at 295 K.

MD Simulations of FraC Nanopores and Peptides.

An all-atom model of the FraC protein was constructed starting from its crystallographic structure, Protein Data Bank entry 4TSY³⁷ taking into account the crystallographic symmetry of the structure. Atoms missing in the crystallographic structure were added using the psfgen tool of VMD.⁶⁵ The structure was then aligned to be coaxial with the z-axis of our coordinate system. The protein was embedded in a pre-equilibrated 16 nm × 16 nm patch of dioctadecatrienoylphosphatidylcholine (DPhPC) bilayer. The lipid bilayer membrane was aligned with the x-y plane and shifted along the z-axis to have the Trp112 residues of the protein located within the same plane as the head groups of the nearest lipid leaflet. Lipid and water molecules that overlapped with the protein were removed. One molar solution of NaCl was added on both sides of the membrane using the solvate and autoionize plugins of VMD, respectively, producing an electrically neutral system of 357,243 atoms. Following assembly, the system was minimized in 1,200 steps using the conjugate gradient method and then equilibrated for 80 ns at a constant number of atoms, pressure and temperature (NPT) ensemble performed while keeping the ratio of the system’s size along the x and y axes constant. During the initial stage of equilibration, all alpha-carbon atoms of the protein were restrained to their initial coordinates using harmonic potentials; the spring constant (k_SPRING) of the potentials was set to 1.0 kcal mol⁻¹ Å⁻² for the first 30 ns and then decreased to 0.8, 0.5 and 0.1 kcal mol⁻¹ Å⁻² in 5 ns steps, following which the system was equilibrated in the absence of any restraints for 35 ns. All subsequent simulations of the FraC protein under applied electric field were performed using the protein structure obtained at the end of last stage of the restrained (k_SPRING = 0.1 kcal mol⁻¹ Å⁻²) equilibration.

The simulations under a transmembrane bias were performed in a constant number of particle, volume and temperature (NVT) ensemble, restraining the protein’s alpha carbon coordinates (k_SPRING = 0.1 kcal mol⁻¹ Å⁻²) to the crystallographic values. For the NVT simulations, the system’s dimensions were set to the average dimensions observed within the last 5 ns of the restrained NPT equilibration. An external electric field E= -V*L_Z was applied along the z-axis (normal to the membrane) to produce a transmembrane bias V, where L_Z is the dimension of the simulated system in the direction of the applied electric field.^40,66

The all-atom structure of the bipolar peptide was obtained by extracting a relatively straight 30-residue fragment from the FraC structure (reside 4 to 34) and mutating the amino acid sequence of the fragment to EEEEEEEEEECGSGSGSKGSRRRRRRRRRR using the psfgen tool. The peptide was solvated in a 7 nm × 7 nm × 6.5 nm volume of 1 M NaCl (28,862 atoms) and equilibration for 50 ns in the NPT ensemble. Two microscopic conformations of the bipolar peptide (stretched and hairpin) were obtained from this MD trajectory by extracting the protein coordinates at 1.6 and 50 ns, respectively. The structure of the truncated peptide was obtained by truncating ten terminal glutamate residues from the stretched structure. Each peptide was placed at the cis entrance of the FraC protein, having the CoM of the terminal arginine residue located 15 Å above (toward the cis side) of the CoM of the FraC’s transmembrane part (defined as residues 4 to 29). Lipid and 1 M NaCl solution were added following the same protocols as above. SI Movies 3,4 and 6 illustrate the starting conformations of the three systems. Each system was minimized 1200 steps and then equilibrated under constant ratio NPT ensemble for 4.8 ns having all alpha-carbon atoms of the protein and the peptide restrained to their initial coordinates (k_SPRING = 0.1 kcal mol⁻¹ Å⁻²). After equilibration, the systems were simulated under applied electric field in the NVT ensemble following the same protocol as described above.

Ion Current Calculation.

Prior to ionic current calculations, frames from the MD trajectory were aligned using protein coordinates to correct for the drift in the x-y plane and lipid bilayer coordinates to correct for the drift along the z-axis. The ionic current was calculated as:

$$I(t)=\frac{1}{\delta t{l}_z}\sum _{j=1}^N{q}_j\delta z_j(t)$$

where δz_j(t) is the displacement of ion j along the z direction during the time interval δt = 4.8 ps and q_j is the charge of ion j. To minimize the effect of thermal noise, the current was calculated within an l_z = 48 Å thickness slab centered at the mid-plane of the lipid bilayer membrane (the slab spanned the entire simulation system in the x-y plane).

Calculation of Electrostatic Potential.

To visualize the electrostatic potential in our systems, we averaged the instantaneous distributions of the electrostatic potential over the MD trajectory using a previously described method,⁴⁰ implemented in the PMEpot plugin of VMD. Each atom of the system was approximated by a spherical Gaussian:

$${\rho }_i(r)=q_i(\frac{\beta }{\sqrt{\pi }}{)}^3{e}^{-\beta \mid r-r_i{\mid }^2}$$

where β was the Gaussians’ width. The instantaneous distribution of the electrostatic potential corresponding to the instantaneous charge configuration was obtained by solving the Poisson equation:

$${\nabla }^2\varphi (r)=4\pi \sum _i{\rho }_i(r)$$

To obtain the average distribution of the potential in a given MD simulation, instantaneous distributions of the potential were averaged over the entire MD trajectory. Three-dimensional (3D) electrostatic potential maps were obtained by averaging the last 48 ns fragments of MD trajectories; β=0.1 β=0.1 A⁻¹ was used for these calculations. One-dimensional profiles of the electrostatic potential through the nanopores were obtained by taking values from the 3D profiles along the z-coordinate, which is also the nanopore axis in our coordinate system.

Calculations of Residue Density.

The residue density of the peptides confined to the FraC constriction region was computed as the ratio of the number of peptide residues located within the FraC constriction to the height of the constriction, 2.8 nm. The constriction region was defined by the average z coordinate of residues Ala5 and Leu23. The number of peptide residues within the constriction was determined as the ratio of the number of peptide backbone atoms within the constriction to the number of backbone atoms in one peptide residue. The peptide density was averaged over the last 72 ns of the respective MD trajectory.

Peptide Design and Synthesis.

The peptides used in this work were a peptide with sequence EEEEEEEEEECGSGSGSKGSRRRRRRRRRR (HPLC purity= 95.8%, MW= 3678.9 Da), and the truncated peptide with sequence SGSGCGSKGSRRRRRRRRRR (HPLC purity= 99.1%, MW= 2387 Da). Peptides were synthesized by Biomatik Corporation (Cambridge, CA). The synthesis was performed using standard solid-phase methods and the peptides were further purified using reverse phase HPLC and analyzed by mass spectrometry (Biomatik). Peptides were kept lyophilized or, when necessary, aliquoted to a final concentration of 10 mg/ml at −20º C.

FraC Expression and Purification.

WT FraC was expressed and purified as described before.^38,39 E. cloni® EXPRESS BL21(DE3) cells were transformed with the pT7-SC1 plasmid, containing the FraC gene with an N-terminus His6-tag. Transformed cells were moved into 200 ml fresh 2-YT media with 100 mg/l ampicillin. The cell culture was grown at 37º C with shaking at 220 rpm, until it reached an optical density of 0.8 at 600 nm. 0.5 mM IPTG was added to the culture to induced FraC expression, after which the growth was continued overnight at 25º C. Cells were harvested by centrifugation at 2000xg for 30 min, and the pellets were stored at −80º C. The pellets (derived from 50–100 mL of bacterial culture) were thawed and resuspended in lysis buffer containing 15 mM Tris base pH 7.5, 1 mM MgCl₂, 4 M Urea, 0.2 mg/ml lysozyme, and 0.05 units/ml DNase. The culture was sonicated to fully disrupt the cells and the crude lysate was then centrifuged at 5400xg for 20 minutes at 4ºC. The supernatant solution was mixed with 100 ul of NiNTA slurry (Qiagen) at room temperature for one hour with gentle mixing. The mixture was spun down at 2000xg for 5 minutes at 4º C. The pellet containing the resin and the protein bound was transferred to a spin column (BioRad). The beads were washed once and eluted with 300 mM imidazole. Protein concentration was estimated using NanoDrop. The monomers were stored at 4º C until oligomerized.

Sphingomyelin and DPhPC (Avanti Polar Lipids) were mixed in a 1:1 ratio and dissolved in 4 ml pentane (Sigma-Aldrich) with 0.5% ethanol. The mixture was placed in a rounded flask and rotated slowly to evaporate the solvent and allow the lipid film to deposit in the walls of the flask. The lipid film was resuspended using a sonicator bath in a buffer containing 150 mM NaCl, 15 mM Tris-HCl (pH 7.5) to a final lipid concentration of 10 mg/ml. The liposomes were stored at −20º C.

Monomeric FraC was mixed with the liposomes in a lipid:protein ratio of 10:1. The mixture was briefly sonicated and incubated for 30 minutes at 37º C. The proteo-liposomes were solubilized with 0.6% LDAO and then diluted 20 times with buffer containing DDM (150 mM NaCl, 15 mM Tris base, pH 7.5, 0.02% DDM). A second round of purification was performed using Ni-NTA beads. Ni-NTA slurry was incubated with the protein/lipid mixture for 1h with gentle shaking. Afterwards, the mixture was loaded into a spin column, washed and eluted using 200 mM EDTA, 75 mM NaCl, 7.5 mM Tris base, pH 8, 0.02% DDM. Oligomers are kept at 4º C for several months.

Electrical Recording in Planar Lipid Membranes.

Electrical recording was performed using planar lipid membranes (BLMs) as has been described before. ^67,68 Briefly, a 25 um-thick Teflon film (Goodfellow Corporation, Pennsylvania USA) containing an orifice of approximately 70 um separates the cis and trans compartments. To form the membranes, 10 ul of 5% hexadecane in pentane is added to the Teflon film and the pentane is allowed to evaporate. The reservoirs are filled with buffer and 10 ul of 10 mg/ml DPhPC in pentane. Membranes were spontaneously formed using the Montal-Mueller method. Ag/AgCl electrodes are placed in each compartment, with the ground electrode in the cis side. WT FraC oligomers are added to the cis side of the chamber. Upon pore insertion, the pore is characterized by measuring traces at different voltages and taking an I-V curve. For the single-channel conductance measurements, nanopores were measured at 0, −50 and 50 mV. The substrate was added to the cis side of the chamber and measured at multiple voltages.

Single-Peptide Stretching and Compressing Experiments.

For the single-peptide stretching experiments, a protocol that generates steps at different voltages was created using the pCLAMP software from molecular devices. Two main modalities were recorded. The first one is a stretching protocol in which the voltage starts at 0 mV, then decreases to −30 mV for 500 ms for peptide capture, and sequentially decreases to −50, −70 and −90 mV for 5 ms at each voltage. The second protocol was a stretching and compressing protocol in which the voltage starts at 0 mV, then decreases to −30 mV for 500 ms, and then is sequentially decreased down to −70 mV and increased again to −30 mV in steps of 10 mV for 5 ms in each step. For the experiments peptide was added to the cis side of the chamber and both voltage protocols were applied and recorded.

Data Acquisition and Analysis.

Nanopore recording were collected using a patch-clamp amplifier (Axopatch 200B, Molecular Devices, USA) at a filtering frequency of 100 kHz. The data was digitized using a Digidata 1550B (Molecular Devices, USA) at a sampling frequency of 500 kHz. The signal was low-pass filtered at 5 kHz and processed using the Clampfit software, a Matlab script, and the software package Transalyzer.⁶⁹