Locality Adaptive Multi-modality GANs for High-Quality PET Image Synthesis

Abstract

Positron emission topography (PET) has been substantially used in recent years. To minimize the potential health risks caused by the tracer radiation inherent to PET scans, it is of great interest to synthesize the high-quality full-dose PET image from the low-dose one to reduce the radiation exposure while maintaining the image quality. In this paper, we propose a locality adaptive multi-modality generative adversarial networks model (LA-GANs) to synthesize the full-dose PET image from both the low-dose one and the accompanying T1-weighted MRI to incorporate anatomical information for better PET image synthesis. This paper has the following contributions. First, we propose a new mechanism to fuse multi-modality information in deep neural networks. Different from the traditional methods that treat each image modality as an input channel and apply the same kernel to convolute the whole image, we argue that the contributions of different modalities could vary at different image locations, and therefore a unified kernel for a whole image is not appropriate. To address this issue, we propose a method that is locality adaptive for multimodality fusion. Second, to learn this locality adaptive fusion, we utilize 1 × 1 × 1 kernel so that the number of additional parameters incurred by our method is kept minimum. This also naturally produces a fused image which acts as a pseudo input for the subsequent learning stages. Third, the proposed locality adaptive fusion mechanism is learned jointly with the PET image synthesis in an end-to-end trained 3D conditional GANs model developed by us. Our 3D GANs model generates high quality PET images by employing large-sized image patches and hierarchical features. Experimental results show that our method outperforms the traditional multi-modality fusion methods used in deep networks, as well as the state-of-the-art PET estimation approaches.

1. Introduction

As a nuclear imaging technology, positron emission topography (PET) has been increasingly used in clinics for disease diagnosis and intervention. It enables the visualization of metabolic processes of human body by detecting pairs of gamma rays emitted indirectly from the radioactive tracer injected into the human body. However, the radioactive exposure inevitably raises concerns for potential health hazards. Nevertheless, lowering the tracer dose will introduce noises and artifacts, thus degrading the PET image quality to a certain extent. Therefore, it is of great interest to synthesize the high-quality full-dose PET (F-PET) image from the low-dose PET (L-PET) image to reduce the radiation exposure while maintaining the image quality. Modern PET scans are usually accompanied by other modalities, such as computed tomography (CT) and magnetic resonance imaging (MRI). By combining functional and morphologic information, PET/MRI system could increase diagnostic accuracy for various malignancies. Previous research also indicates the benefit brought by multi-modality data to PET image quality enhancement [1–3].

There have been some works for F-PET image synthesis. Most of them, however, are based on voxel-wise estimation methods, e.g., random forest regression method [1], mapping-based sparse representation method [2], semi-supervised tripled dictionary learning method [4], and multi-level canonical correlation analysis (CCA) framework [5]. These methods are all based on small patches and the final estimation of each voxel is determined by averaging the overlapped patches, resulting in over-smoothed images that lack the texture of a typical F-PET image.

In recent years, deep learning has been used to improve image synthesis. Dong et al. [6] proposed a convolutional neural networks (CNNs) model for image super-resolution. With the similar architecture, Li et al. [7] estimated the missing PET image from MRI for the same subject. More recently, generative adversarial networks (GANs) have also showed their superior performance in many image synthesis tasks [8]. In the literature, the incorporation of multi-modality data in deep learning models is usually conducted in a global manner. For example, in CNN-based deep learning models such as two recent multi-channel GANs models [9], multi-modalities are treated as multiple input channels, and for each channel a unified kernel (invariant to image locations) is applied for the convolution over the whole image. Such a kind of multi-modality fusion is referred to as the multi-channel method in this paper. However, we argue that the contributions of different modalities could vary at different image locations, and therefore a unified kernel for a whole image is not appropriate.

In this paper, inspired by the appealing success of GANs and also motivated to tackle the limitation of the current multi-channel deep architectures, we propose a “locality adaptive” multi-modality GANs (LA-GANs) model to synthesize the F-PET image from both the L-PET and the accompanying T1-weighted MRI images. The contributions of our method are as follows. (1) We propose a new mechanism to fuse multi-modality information in deep neural networks. The weight of each imaging modality varies with image locations to better serve the synthesis of F-PET. (2) Using multi-modality (especially making it locality adaptive) may induce many additional parameters to learn. We therefore propose to utilize 1 × 1 × 1 kernel to learn such locality adaptive fusion mechanism to minimize the increase on the number of parameters. Doing so also naturally leads to a fused image that acts as a pseudo input for the subsequent learning stages. (3) We develop a 3D conditional GANs model for PET image synthesis, and jointly learn the proposed locality adaptive fusion with the synthesis process in an end-to-end trained manner. Our 3D GANs model generates high quality PET images by employing large-sized image patches and hierarchical features.

2. Methodology

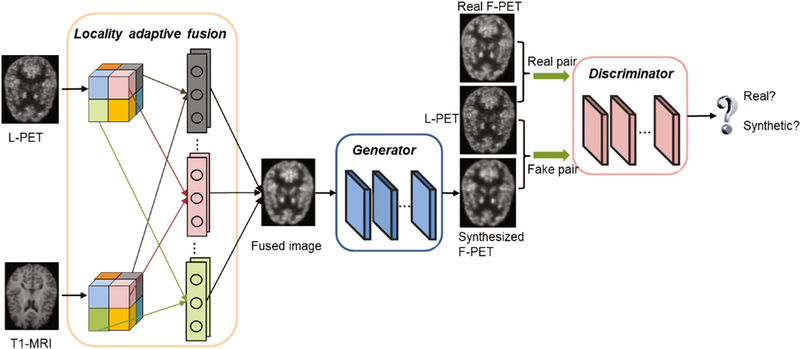
The proposed LA-GANs model is illustrated in Fig. 1, which consists of three parts: (1) the locality adaptive fusion network, (2) the generator network, and (3) the discriminator network. Concretely, the locality adaptive fusion network takes both an L-PET and a T1-MRI as input and generates a fused image by learning different convolutional kernels at different image locations. After that, the generator network produces a synthesized F-PET from the fused image, and the discriminator network subsequently takes a pair of images as input, i.e., the L-PET and the real or synthetic F-PET, and aims to distinguish between the real and synthetic pairs. When the discriminator can easily distinguish between them, it means that the synthesized F-PET has not well resembled the real one, and that the fusion network and the generator network should be further improved to produce more realistic synthesis. Otherwise, the discriminator should be enhanced instead. Therefore, the three networks are trained jointly with the discriminator network trying to correctly distinguish between the real and synthetic F-PET, while the fusion and generator networks trying to produce realistic images that can fool the discriminator. Please note that, we use 3D operations for all the networks to better model the 3D spatial information.

Fig. 1.

Overview of the proposed pipeline for full-dose PET (F-PET) synthesis from low-dose counterpart (L-PET) and the accompanying T1-MRI image.

2.1. Architecture

Locality Adaptive Fusion Network

This is a module for multi-modality information fusion. As mentioned before, in most multi-channel based networks, image convolution is performed in a global manner, i.e., for each modality the same filter is applied to all image locations to generate the feature maps that will be combined in higher layers. This could not effectively handle the location-varying contributions from different imaging modalities. To tackle this problem, locality adaptive convolution should be enforced. However, if the locality adaptive convolution is simply conducted in the multi-channel framework, many additional parameters will have to be learned due to adding new imaging modalities. This is not favorable for medical applications where the number of the training samples is often limited. Therefore, we propose to add a module that produces a fused image from multi-modality images and use the fused image as the pseudo input to the generator network. In this way, the increase of the number of modalities will not cause any increase on the number of parameters in the generator. Moreover, we propose to utilize 1× 1 × 1 kernel for locality adaptive convolution to minimize the number of necessary parameters to learn in this fusion module. The fusion network will be jointly learned with the generator and the discriminator to ensure that they can effectively negotiate with each other to achieve the best possible performance on image synthesis. Specifically, the entire L-PET and T1-MRI images are partitioned, respectively, into N non-overlapping small patches, i.e., $P_i^L$ and $P_i^{T1}(i=1,\dots ,N)$, as indicated by the patches in different colors in Fig. 1. Then, the two patches at the same location (indicated by using the same color) from the two modalities, i.e., $P_i^L$ and $P_i^{T1}$, are convolved, respectively, using two different 1 × 1 × 1 filters with parameters $w_i^L$ and $w_i^{T1}$. For instance, in the fusion block in Fig. 1, the two gray filters are respectively operated on the two gray patches of the L-PET and T1-MRI images to generate their corresponding combined patch. Formally, the combined patch $P_i^C$ is obtained as follows:

$$\begin{gathered} P_i^C=w_i^L\ast P_i^L+w_i^{T1}\ast P_i^{T1}, \\ \text{s.t.}{w}_i^L+w_i^{T1}=1;w_i^L>0;w_i^{T1}>0,i=1,\dots ,N \end{gathered}$$ (1)

In this way, we will learn N pairs of different convolution kernels for N local patches. The outputs of the fusion are further assembled to form an entire fused image as the input of the following generator network.

Generator Network

In our generator network, we adopt both the convolutional layers and de-convolutional layers to ensure the same size of the input and output. Since the L-PET and F-PET images belong to the same modality, there is a lot of low-level information shared between them. As such, we follow the U-Net and add skip connections between the convolutional and de-convolutional layers, thus combining hierarchical features for better synthesis. Also, the skip connection strategy mitigates the vanishing gradient issue, allowing the network architecture to be much deeper.

Our network architecture (more details in the supplementary) contains multiple Convolution-BatchNormalization-LeakyRelu components. Specifically, it constitutes 12 3D convolutional layers. In the encoder part which includes the first 6 convolutional layers, we use 4 × 4 × 4 filters and a stride of 2 for convolution, and 0.2 negative slope for the leaky ReLu. The number of feature maps increases from 64 in the 1^st layer to 512 in the 6^th layer. In the decoder part, we perform up-sampling with a factor of 2.

Discriminator Network

The discriminator network is a typical CNN architecture consisting of 4 convolutional layers, and each of them uses 4 × 4 × 4 filters with a stride of 2, similar to the encoder structure of the generator. The first convolution layer produces 64 feature maps, and this number is doubled at each of the following convolutional layers. On top of the convolutional layers, a fully connected layer is applied and followed by a sigmoid activation to determine whether the input is the real pair or the synthetic one.

2.2. Objective Functions

Let us denote x_L an L-PET image, x_T1 the accompanying T1-MRI image, and y_F the corresponding real F-PET image (i.e., the ground truth annotation). In this study, we learn three function mappings. The first mapping $F_{\alpha }:\left(x_L\in {ℝ}_{Low},x_{T1}\in {ℝ}_{T1-MRI}\right)\to {\overline{y}}_F\in {ℝ}_{Fused}$ is for the locality adaptive fusion network, which produces a fused image ${\overline{y}}_F$ from x_L and x_T1. The second mapping $G_{\beta }:{\overline{y}}_F\in {ℝ}_{Fused}\to {\overline{\overline{y}}}_F\in {ℝ}_{Synthetic}$ is for the generator network, which maps the fused image ${\overline{y}}_F$ to a synthetic F-PET image ${\overline{\overline{y}}}_F$. The third mapping corresponds to the discriminator network function $D_{\gamma }:(x_L\in {ℝ}_{Low},x_{T1}\in {ℝ}_{T1-MRI},Y_F\in {ℝ}_{Full})\to d\in [0,1]$, whose task is to distinguish the synthetic pair $Y_F:=\left(x_L,{\overline{\overline{y}}}_F\right)$ (ideally d → 0) from the real pair Y_F := (x_L, y_F) (ideally d → 1). The symbols α, β and γ denote the parameter sets of the three networks, respectively, and are automatically learned from a training set ${\left\{\left(x_L^i,x_{T1}^i,y_F^i\right)\right\}}_{i=1}^m$. Formally, we solve the following optimization problem

$$\begin{gathered} \underset{\alpha }{\min }\underset{\beta }{\min }\underset{\gamma }{\max }V\left(F_{\alpha },G_{\beta },D_{\gamma }\right)= \\ \mathbb{E}\left[\log D_{\gamma }\left(x_L,y_F\right)\right]+\mathbb{E}\left[\log \left(1-D_{\gamma }\left(x_L,G_{\beta }\left(F_{\alpha }\left(x_L,x_{T1}\right)\right)\right)\right)\right]+\lambda V_{L1}\left(F_{\alpha },G_{\beta }\right), \end{gathered}$$ (2)

with λ > 0 being a trade-off constant. The last term is an L1 loss, used to ensure that the synthetic F-PET image stays close to its real counterpart. The L1 loss is defined as

$$V_{L1}\left(F_{\alpha },G_{\beta }\right)=\mathbb{E}\left[{\Vert y_F-G_{\beta }\left(F_{\alpha }\left(x_L,x_{T1}\right)\right)\Vert }_1\right].$$ (3)

Please note that, the fusion network F and the generator network G, in a sense, can be regarded as a whole network whose goal is to synthesize realistic-looking F-PET images that can fool the discriminator network D. Following the approximation scheme in [10], the term log (1 – D_γ(x_L, G_β(F_α(x_L, x_T1)))) can be replaced by minimizing a simpler form −logD_γ(x_L, G_β(F_α(x_L, x_T1))). Therefore, training the fusion network F and generator network G equals minimizing

$$L_{\mathcal{F},\mathcal{G}}\left(F_{\alpha },G_{\beta }\right)=-{\sum }_i\log D_{\gamma }\left(x_L^i,G_{\beta }\left(F_{\alpha }\left(x_L^i,x_{T1}^i\right)\right)\right)+\lambda {\sum }_i\left({\Vert y_F-G_{\beta }\left(F_{\alpha }\left(x_L^i,x_{T1}^i\right)\right)\Vert }_1\right).$$ (4)

On the other hand, the discriminator network D tries to tell the real pair (x_L, y_F) from the synthetic pair $\left(x_L,{\overline{\overline{y}}}_F\right)$ by maximizing Eq. (2). Therefore, training the discriminator network corresponds to maximizing

$$L_{\mathcal{D}}\left(D_{\gamma }\right)={\sum }_i\left(\left[\log D_{\gamma }\left(x_L^i,y_F^i\right)\right]+\log \left(1-D_{\gamma }\left(x_L^i,G_{\beta }\left(F_{\alpha }\left(x_L^i,x_{T1}^i\right)\right)\right)\right)\right).$$ (5)

2.3. Training LA-GANs

The fusion network F together with the generator network G and the discriminator network D are trained in an alternating manner as [10]. Specifically, we first fix F and G to train D, and then fix D to train F and G. As shown in Eq. (2), the training of F, G and D is just like playing a min-max game: F and G try to minimize the loss function while D tries to maximize it, until an equilibrium is reached. In the test stage, only the fusion and generator networks are needed for synthesis. All networks are trained by Adam solver with mini-batch stochastic gradient descent (SGD) and the mini-batch size is 128. The training process runs for 200 epochs, and the learning rate is set to 0.0002 for the first 100 epochs, and then linearly decays to 0 in the second 100 epochs.

3. Experiments and Results

We validate our proposed method on a real human brain dataset consisting of 8 normal control (NC) subjects and 8 mild cognitive impairment (MCI) subjects, each with an L-PET image, a T1-MRI image and an F-PET image. Subjects were administered an average of 203 MBq of [¹⁸F]FDG. The PET scans were acquired by a Siemens Biograph mMR PET-MR scanner. For each subject, the PET images are aligned to its T1-MRI to build the voxel-level correspondence via affine transformation. Each aligned image has the resolution of 2.09 × 2.09 × 2.03 mm³ and the image size of 128 × 128 × 128. Considering the small number of the training samples, we extract 125 large 3D image patches of size 64 × 64 × 64 from each image, rather than directly using the entire 3D image, to train the deep model. In addition, to make full use of available samples, we follow the widely used “Leave-One-Subject-Out” strategy. To train the proposed locality adaptive convolution network, we further partition each large image patch into 4096 non-overlapping 4 × 4 × 4 regions for fusion. Our method is implemented by PyTorch, and all the experiments are carried out on an NVIDIA GeForce GTX 1080 Ti with 11 GB memory.

Comparison with the State-of-the-Art PET Estimation Methods

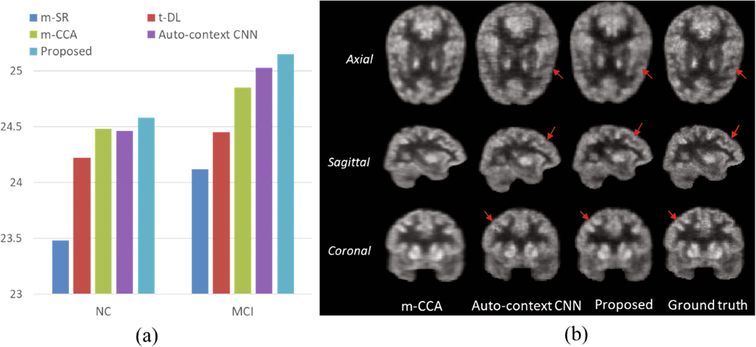
We compare our method with the following state-of-the-art multi-modality based PET estimation methods: (1) mapping based sparse representation method (m-SR) [2], (2) tripled dictionary learning method (t-DL) [4], (3) multi-level CCA method (m-CCA) [5], and (4) auto-context CNN method [3]. The averaged PSNR are given in Fig. 2(a), from where we can see that our proposed method outperforms all the other competing methods, demonstrating its effectiveness and advantages. In Fig. 2(b), we show an example visual result of our method compared with two methods (m-CCA and auto-context CNN) which produce the top two results in the literature. As observed, the estimated images by the m-CCA method are over-smoothed compared with the real F-PET images due to the averaging of the overlapping patches to construct the final output images. Compared with the auto-context CNN network, our model tends to better preserve the detailed information in the estimated F-PET images, as indicated by the red arrows. We argue that this is because the adversarial training network used in our model constrains the synthesized images to be similar to the real ones.

Fig. 2.

Comparison with the state-of-the-art PET estimation methods.

Comparison with our method using single-modality or multi-channel strategy

To study the contribution of the anatomical information from MRI for PET synthesis and evaluate the effectiveness of the locality adaptive fusion network of our proposed model, we further conduct experiments to compare our method with its two variants: one using only single modality of L-PET [11], and the other using the common multichannel strategy [9] for multi-modality. The results are reported in Table 1. First, we can see that our method obtains higher PSNR than the single-modality L-PET variant (p-value in paired t-test: 0.0092 for NC and 0.0036 for MCI), indicating that the anatomical information from MRI yields important cues for PET synthesis. Second, compared with the multi-channel variant, our method boosts the averaged PSNR approximately 0.28 and 0.2 for NC and MCI groups, respectively. The standard deviation of our method is also smaller than that of the multi-channel GANs while the median is higher. Also, the paired t-test indicates that our improvement from the multichannel one is statistically significant (p < 0.05). Moreover, it is found that the number of increased learning parameters induced by adding T1-MRI is 4096 for our method and 8192 for the multi-channel GANs, suggesting that our model produces better performance with less parameters to learn.

Table 1.

Quantitative comparison with two variants of our method (single-modality GANs and multi-channel GANs) in terms of PSNR. Here, Med. means median.

Method	NC subjects			MCI subjects
	Mean (std.)	Med.	p-value	Mean (std.)	Med.	p-value
L-PET	19.88 (2.34)	20.68	7.7E–05	21.33 (2.53)	21.62	2.3E–−04
Single-modality	23.94 (2.04)	24.78	0.0092	24.37 (1.95)	24.85	0.0036
Multi-channel	24.31 (1.91)	24.59	0.0391	24.95 (2.01)	25.30	0.0071
Proposed	24.58 (1.78)	25.21	–	25.15 (1.97)	25.49	–

We also provide a visual comparison in Fig. 3, where the two leftmost images are the input T1-MRI and L-PET images and the rightmost image is the ground-truth F-PET. We can clearly see that the synthesized F-PET image of our proposed model has less artifacts than those of the single-modality method and the multi-channel method, as indicated by the red arrows.

Fig. 3.

Visual comparison with single-modality and multi-channel GANs methods.

4. Conclusion

In this work, we proposed a 3D locality adaptive multi-modality GANs model for synthesizing high-quality PET images from the L-PET and T1-MRI images. Both qualitative and quantitative results demonstrate that our method significantly outperforms the traditional multi-modality fusion methods used in deep networks, as well as the state-of-the-art PET estimation approaches. Our model could also be applied to other related applications such as mapping one or two modalities to another modality. In the future, we will investigate the potential of our model for general synthesis tasks as well.