Data-Driven Model Validation Across Dimensions

Abstract

Often in mathematical and computational biology, assumptions are made (e.g. symmetry) to reduce the problem from three spatial dimensions (3D) to two (2D). However, some experimental datasets, such as cell counts obtained via flow cytometry, represent the entire 3D biological object. For purposes of model calibration and validation, it is sometimes necessary to compare these biological datasets with model outputs. We propose a methodology for scaling 2D model outputs to compare with 3D experimental datasets, and we discuss the application of this methodology to two examples: agent-based models of granuloma formation and skeletal muscle tissue. The accuracy of the method is evaluated in artificially generated scenarios.

1. Introduction

Mathematical and computational modeling have been applied to study many different areas of biology. One necessary step in performing a modelling study is to create a model that reflects the biology of the system. Representing biological structures that are cylindrical (such as muscle fibers), spherical (such as some tumors), or even kidney-bean shaped (such as lymph nodes) is sometimes difficult to do in three dimensions due to computational or mathematical issues. Modelers often make simplifying assumptions in order to decrease the dimensionality of the problem. Carrying out two-dimensional (2D) mathematical analysis and 2D simulations are significantly easier, faster, and usually cheaper than their three-dimensional (3D) counterparts, making them an attractive option for modelers. What becomes necessary, however, is to calibrate and/or validate these models against datasets derived from the biological system. Many different types of data are generated from experimental systems, and they can represent the entire three-dimensional biological object. Thus, outcomes from the mathematical or computational model must be scaled in some way from 2D to accurately capture these datasets in 3D. How to scale two-dimensional model outcomes to compare with three-dimensional datasets becomes an important issue to calibrate or validate models.

In this note we focus on two examples to illustrate the scaling of 2D model outputs to 3D datasets. We consider the case of a hybrid computational agent-based models that describes formation and function of tuberculosis granulomas as well as that of skeletal muscle, but the ideas and methods presented herein are applicable to other biological phenomena.

1.1. ABM of granulomas

Our hybrid computational agent-based model, GranSim, describes granuloma formation and function in lungs (10; 3). There are three central elements of our approach, which has been implemented in both 2D, Figure 1A, [malthus.micro.med.umich.edu/GranSim] and 3D [malthus.micro.med.umich.edu/3D-GranSim, (6)], Figure 1B. First, we use an agent-based model (ABM) to describe cellular behavior, including recruitment, activation, and movement. Three populations of bacteria (intracellular replicating, extracellular replicating and extracellular non-replicating bacteria) are represented as continuous functions in the extra- or intra-cellular environment. Classes of T cells, namely naïve and effector IFN-γ producing, regulatory, and cytotoxic T cells, are tracked. Probabilistic interactions between immune cells and bacterial populations are described by rules that are continuously updated (rules at: http://malthus.micro.med.umich.edu/lab/movies). Second, we capture receptor/ligand binding and trafficking and intracellular signaling events with ordinary differential equations (ODEs) that are solved within each agent (cell) or on the grid. Here we use an approach we term tunable resolution: toggling between fine-grained (detailed) and coarse-grained (less detailed) descriptions of events as needed for the questions being asked (5). Using fine-grained models to inform the construction of coarser-grained models has allowed us to construct more computationally tractable models. Third, we describe diffusion of relevant soluble ligands (e.g. cytokines, antibiotics) by solving the relevant partial differential equation (PDE) numerically. Equations and parameters for all portions of the model were built based on extensive biological and biochemical data. These three model elements are linked, allowing information to be continually exchanged across biological scales in a computationally efficient manner (1). Each simulation follows events in space and time over several hundred days, building over time to track thousands of individual cells. Overall, our multi-scale GranSim simulates molecular and cellular scale immunologic events, with tissue-scale behavior (granuloma formation) as an emergent feature of the simulation. This results in generation of numerous granuloma types that evolve over space and time with different bacterial numbers and trajectories.

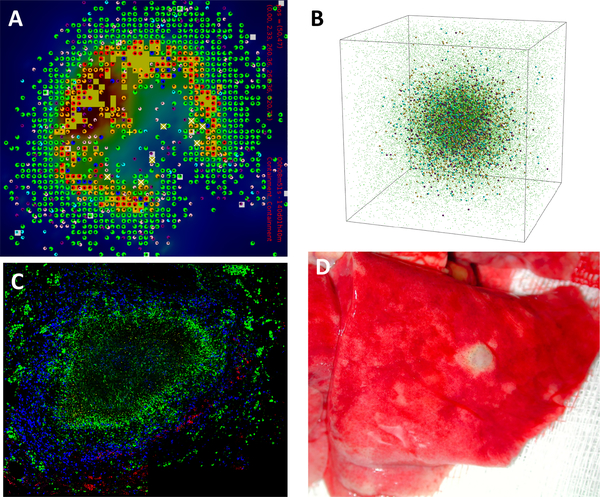
Fig. 1. Simulated and experimental granulomas.

Panel A: Snapshot in space and time of the granuloma simulator in 2D, GranSim. The grid is a 2mm x 2mm section of simulated lung tissue that is vascularized with source compartments. Panel B: Snapshot in space and time of the granuloma simulator in 3D. In both Panels A and B, Colors represent resting (green), activated (blue), infected (orange), chronically infected (red), T cells (pink: IFN-γ producing, purple: cytotoxic, white: regulatory), extracellular bacteria (yellow), necrosis (brown areas). Panel C: immunohistochemistry staining of a 2D slice of a non-human primate granuloma stained for macrophages (green CD68), B cells (red CD20) and T cells (blue CD3). The very center (black, no staining) is caseous necrosis (Image courtesy of Dr. Josh Mattila, University of Pittsburgh). Panel D: whole lung (red) from non-human primate showing a 3D granuloma (white portion, Image courtesy of Dr. JoAnne Flynn, University of Pittsburgh).

Our granuloma simulations are computationally intensive. Individual simulations take approximately 200 hours for a 100×100×100 3D grid, whereas they take only and 3–4 hours for a 100×100 2D grid. Thus, running simulations in 3D requires an increase in computing time of about two orders of magnitude. Because the simulation is stochastic, multiple simulations are required for each parameter set or experimental condition to amass data on simulation outcomes. For purposes of model calibration and parameter sensitivity analysis, we will often run simulations for 1,000 different parameter sets, each with multiple replicates. Due to the vast computational expense, we most often use the 2D version of the model, imagining it to represent a slice through the center of a 3D structure.

Data on bacterial levels from whole granulomas were provided from our experimental collaborators, and these datasets are derived from 3D structures (c.f. Figure 1D)¹. Since the model that we use most often represents a 2D slice (see Figure 1A,C), we scale our model output of bacterial numbers to the 3D datasets provided. In (2), we used a scaling procedure to compare the two-dimensional bacterial output of GranSim with data from whole lesions in non-human primates. For the scaling, we calculated the minimum radius of a circle that could encompass the entire 2D bacterial population and determined an appropriate two-dimensional to three-dimensional scaling factor. To determine the radius, we computed the total area occupied by grid compartments containing at least one bacterium (A = NΔx², where N is the number of grid compartments containing bacteria), and then computed the radius of the circle with the same area (A = πr², or $r=\sqrt{A/\pi }$). The scaling factor was then determined as the ratio of the volume of the sphere of radius r to the volume of a circular slice of radius r that is one grid compartment thick, i.e. $SF=\frac{(4/3)\pi r^3}{\Delta x\pi r^2}$.

Since this procedure involves compressing the bacteria into the smallest sphere that could contain them, it systematically underestimates bacterial counts. While there is error of underestimation here, it is minimal for bacteria populations that exist primarily in the center of a granuloma. It is more significant, however, if we apply it for use with other cell types such as T cells or macrophages that comprise the outer bands of a granuloma (see Figures 1A,C). The error is also significant if the cell density is relatively low but the granuloma is large in size.

2. New scaling method

We propose a new scaling procedure that is applicable to any spherical structure including granulomas and tumors. With slight modification, this procedure can be applied to certain non-spherical structures as well, e.g. cylindrical structures such as blood vessels.

There are two major factors that must be considered in improving upon the previous method. First, we seek to utilize information about the true size of a simulated granuloma in our scaling, rather than imagining cells re-positioned into the smallest possible area. This will prevent systematic underestimation and help to minimize the error in our method. Second, since cell density may vary with distance from the center of the granuloma, we cannot assume a constant density throughout the entire sphere. Thus, we propose to partition the granuloma into annuli of increasing radii, spanning from the center all the way to the outer edge of the structure, and then perform a 2D to 3D scaling for each annulus. To this end, having an accurate way to determine the boundary of the structure is necessary to signal that the edge has been reached. We will discuss this in Section 3.

2.1. Details of the method

After the simulation is performed and a 2D spatial structure is obtained, we utilize the following procedure to scale to 3D cell counts.

1. Construct a disk centered at the center of the granuloma that encompasses all granuloma cells. For the case of cells on a grid, this is done via the boundary identification method presented in Section 3.

2. Partition this disk into a series of annuli, centered at the center of the granuloma, with increasing radius. For simplicity, we will use annuli of equal thickness, though this is not required. This is illustrated in Figure 2.

3. For each annulus, count how many cells are inside the annulus. Multiply by the scaling factor

   $$SF=\frac{\text{Volume}\text{of}\text{spherical}\text{shell}}{\text{Volume}\text{of}\text{cross-sectional}\text{slice}}=\frac{\frac{4}{3}\pi \left(r_i^3-r_{i-1}^3\right)}{h\pi \left(r_i^2-r_{i-1}^2\right)}$$

   to compute how many cells would be inside the 3D spherical shell. Here, h is the assumed height of the cross-sectional slice. In practice, h should be at least the diameter of a single cell but should be small with relation to the object to maintain accuracy.

4. Sum up all the cells to get how many are in the entire sphere.

Fig. 2. Illustration of the scaling method.

A disk containing the granuloma is partitioned into a series of annuli. For each annulus, the cell count is scaled to 3D by scaling the annulus to a spherical shell.

This procedure depends on the object of interest being spherical in nature. If the object were, say, a cylinder instead of a sphere (e.g. a blood vessel or muscle fiber), then one could use cylindrical shells and the scaling factor would need to be adjusted accordingly.

Computationally, the primary cost of this procedure lies in determining the distance from the center of the granuloma for each grid compartment in the granuloma, since there may be thousands of compartments and the center of the granuloma may change over the course of a simulation. Once the distance is computed for each grid compartment in the granuloma, the compartments can be sorted by distance to loop through the annuli from smallest to largest (or vice versa).

2.2. Testing the new scaling method

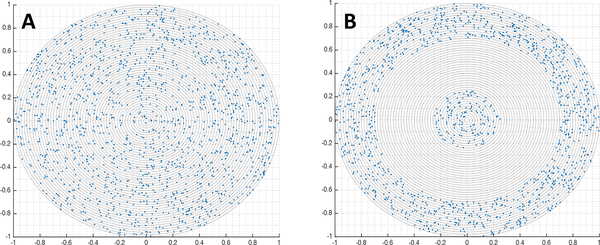
To test the method, we use two different types of object: (a) a sphere, and (b) a spherical shell surrounding a much smaller sphere, with empty space in between. An object similar to (b) could arise, for example, when counting an immune cell that exists in both the caseous center and in the outer cuff of a granuloma. For simplicity, we represent cells as points placed continuously in space rather than on a grid. The cells are placed randomly using the built-in random number generator rand in Matlab. To test the accuracy of the scaling method, we use the following procedure.

1. Randomly populate a 3D object (either a full sphere or a spherical shell surrounding a smaller sphere) with a specified number of cells. We assume that cells are uniformly distributed within the object.

2. Take a cross-section of height h across the equator. Project this to a 2D object.

3. Apply the scaling procedure to the 2D cross-section and compare the result with the original number of cells.

4. Repeat steps (1)–(3) N times using different seeds for the random placement of cells. The choice of N depends on the desired accuracy of the summary statistics; larger N will yield more accurate statistics.

We let the radius of the object be r = 1 and the height of the cross-sectional slice be h = 0.02, so that the height of the cross-sectional slice is 1/100th of the diameter of the object. Table 1 shows scaling results for a variety of different cell counts for both object types. For each experiment, N = 20 replicates were performed to obtain the mean and standard deviation of the estimated number of cells. We observe that the average relative error is less than 1%. The standard deviation of the estimates generally decreases relative to the number of cells as the number (thus also density) of cells increases. Increased cell density leads to smaller relative variation in the number of cells in the 2D cross-section. The standard deviation is roughly 10% for 10,000 cells, 4% for 50,000 cells, and 2.5% for 100,000 cells for both test cases. This method does not systematically over-or under-estimate cell counts. The small amounts of over- and under-estimation in our numerical tests are simply due to random effect.

Table 1.

Results for applying the new scaling procedure to the two test cases in Figure 3. For each experiment, 30 replicates were performed.

Sphere
# of cells	Avg. cells in 2D cross-section	Mean estimate	Std. dev.
10,000	152	10,138	1,080
50,000	750	50,083	1,681
100,000	1,498	99,734	2,396
Shell
# of cells	Avg. cells in 2D cross-section	Mean estimate	Std. dev.
100,000	121	97,745	777
50,000	617	49,787	1,895
100,000	1,235	99,299	2,301

Matlab code to perform the numerical tests are provided in the Supplementary Material.

2.3. Comparison with the previous method

In many agent-based models, cells live and move on a discrete grid rather than in a continuous space. We can translate this scaling procedure to cells placed on a grid by considering a grid compartment to be “inside” a circle if its center is within the circle. Thus a reasonable restraint is Δr ≥ Δx, where Δr denotes the distance between two subsequent circles and Δx denotes the grid-size. We expect to obtain the highest accuracy by choosing _Δr = _Δx. In the equation for the scaling factor, we now have h = Δx, assuming cubical grid compartments.

In this scenario, we can directly compare the accuracy of the proposed method with the previously used scaling procedure from (2) (described above). Table 2 shows scaling results for both the new and old scaling procedures applied to cells on a 100 × 100 grid. In these tests, we used _Δr = _Δx. We see that the previous method does indeed underestimate the cell counts, and that the relative error for the spherical shell example is greater than 50% on average. In the sphere example, since the old scaling procedure relies on compressing the occupied grid compartments into the smallest possible radius, the error decreases as cell density increases; still, the average error is still greater than 50% for 100,000 cells, and is more than 40% for 200,000 cells. The new scaling method, on the other hand, maintains a 1% or smaller average relative error for all of the test cases. This demonstrates a vast improvement over the old scaling method.

Table 2.

Results for applying the new and old scaling procedures to two test cases with cells on a grid. For each experiment, 30 replicates were performed. Results are reported as mean ± standard deviation.

Sphere
# of cells	New scaling	Old scaling
100,000	100,212 ± 2,692	41,793 ± 1,475
200,000	199,196 ± 4,898	112,701 ± 3,465
Shell
# of cells	New scaling	Old scaling
100,000	99,761 ± 3,120	32,019 ± 1,411
200,000	199,645 ± 3,245	85,707 ± 1,925

3. Boundary identification

In both experimental and computational simulations, it is necessary to define the boundary of an object to ensure that the measurements are accurately reflecting the actual structure and not including any extraneous measurements from the surrounding tissue (wetlab) or grid (model). Figures 1C, D show that there are immune cells and lung cells outside of the granuloma boundary. In Figure 1C, there are immune cells that are stained in the lung tissue around the granuloma that are likely being recruited there, but they are not yet part of the granuloma structure. In Figure 1D, it is difficult to cut the granuloma from the lung tissue (using a method known as laser capture microdissection (9) and ensure that no lung tissue is taken along. In fact, the 2D slice in Figure 1C is taken from a 3D granuloma that was excised in that manner. Similarly, in our 2mm×2mm section of lung tissue, Figure 1A,B shows that the model generates cells outside of the granuloma structure as occurs in the actual lung tissue. Thus, to capture solely the cell counts in a simulated granuloma, it is useful to define the boundary of the granuloma, to discriminate between cells within the granuloma and cells that are part of the surrounding tissue. Here, we present a methodology for determining a lower and upper bound for the radius of a granuloma.

First, we construct a network of model grid compartments that are eligible to be included in the granuloma. A compartment is considered eligible if it is either caseous or contains at least one immune cell, and at least N of the compartments in its Moore neighborhood also are caseous or contain at least one immune cell, where N is a parameter that may be tuned. These compartments form the vertices of the network. Two vertices are connected by an edge if the corresponding grid compartments are contained in each other’s Moore neighborhoods. To determine which cells are in the granuloma, we then calculate the connected components of the network. A grid compartment is defined to be in the primary granuloma if it is in the largest connected region of the network. This is illustrated in Figure 4.

Fig. 4. Illustration of the boundary identification method.

(A) Example of classifying grid compartments into granuloma and non-granuloma based on the number of neighbors that are occupied by cells. In this example, we use N = 4 for the number of neighbors that must be occupied. Empty grid compartments correspond to un-involved or healthy tissue. (B) Illustration of a Moore neighborhood. (C) Construction of the network showing connected grid compartments in the granuloma. The boundary of the granuloma is defined to be the boundary of the largest connected component in the network, shown in blue.

We calculate a geometric “center of mass” of the granuloma, C, by taking the average of all grid compartment coordinates

$$C=\frac{1}{M}\sum _{i=1}^M\langle x_i,y_i\rangle$$

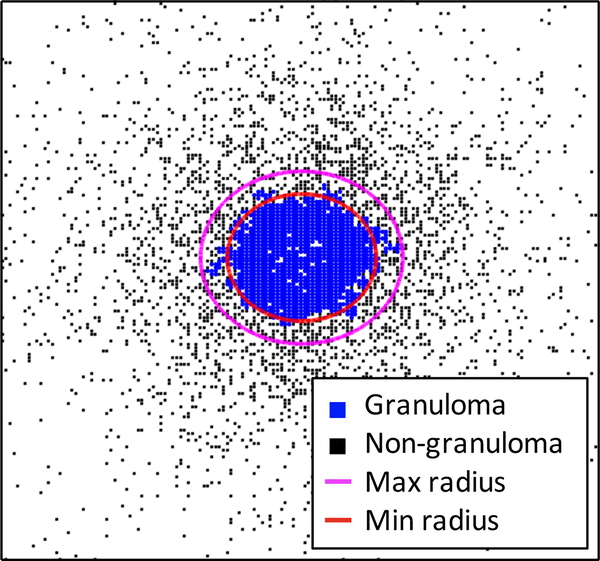
where M is the number of compartments in the granuloma. We call this a geometric center of mass because we do not distinguish between cell types of different sizes, nor do we consider how many cells are contained in each grid compartment. From this center, we calculate an upper bound for the radius of the granuloma by computing the largest distance from the center to any compartment in the granuloma,

$$r_u=\max {\Vert \langle x_i,y_i\rangle -C\Vert }_2.$$

To determine a lower bound for the radius, we compute the radius of the smallest circle that could encompass the total area of all grid compartments in the granuloma, i.e. $\pi r_{\ell }^2=M\Delta x^2$. This gives the formula

$$r_{\ell }=\sqrt{\frac{M}{\pi }}\Delta x.$$

For purposes of applying the scaling procedure, we use the upper bound for the radius to ensure that the entire granuloma is contained. The difference between the upper and lower bounds gives an idea of how round and dense the granuloma is. If a granuloma is perfectly round and all grid compartments inside the granuloma contain cells, then the upper and lower bounds for the radius will be equal.

4. Comparison of ABM, cross-sectional, and flow cytometry data for skeletal muscle

A scaling method similar to what is presented here could be applied to a skeletal muscle system to systematically compare ABM output and the various types of experimental data, and also to help quantify the degree of over- or under-estimation.

We have previously developed a two-dimensional agent-based model to study the confluence of biochemical and mechanical processes underpinning skeletal muscle remodeling (Figure 6). The model predicts measurable and functionally relevant changes in muscle microstructural anatomy, such as changes in muscle fiber cross-sectional area over time, that lead to alterations in muscle force generation. We have used the model to study muscle remodeling caused by different pathologies and injuries, including disuse-induced atrophy (7), laceration-induced acute injury (8), and chronic loss of dystrophin (11). The 2D ABM simulates a transverse cross-section of skeletal muscle and includes agents that represent individual muscle fibers, and immune cells such as fibroblasts, satellite stem cells, and inflammatory cells such as macrophages and neutrophils. The model also simulates extracellular matrix proteins, as well as diffusible chemokines and growth factors.

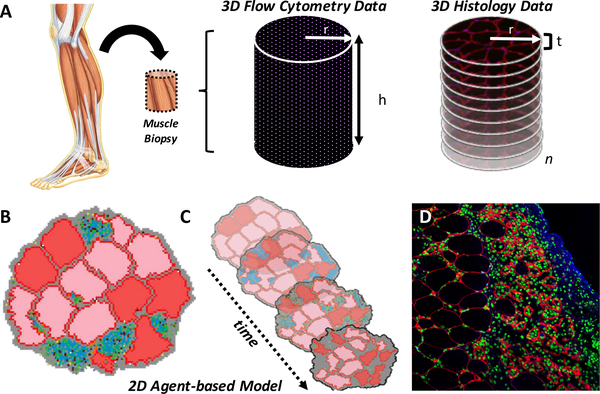
Fig. 6. Simulated and experimental skeletal muscle data.

(A) Muscle biopsies from patients or animal models of disease or injury can be obtained in order to determine the quantity of cells in a volume of muscle using either flow cytometry or by counting cells in adjacent histological sections. (B) Cell counts from these 3D experimental datasets are used to specify the number of agents in the 2D ABM representing a transverse cross-section of muscle, where each agent represents a single cell (muscle fibers in red and pink, neutrophils in green, macrophages in black, and satellite stem cells in light blue) surrounded by extracellular matrix (gray) at the onset of an injury. (C) The ABM predicts functionally important changes in muscle microstructure over time (e.g. days to weeks), such as alterations in muscle fiber cross-sectional area (pink and red fibers changing size and cross-sectional shape) and thickening of the extracellular matrix (gray), or scar formation. (D) ABM predictions are compared, or validated against, immune-stained 2D histological cross-sections of injured and healing muscle that indicate the number and locations of different cell types, such as macrophages (green) surrounded by remodeled muscle fibers (outlined in red) and scar tissue (blue).

Specifying a biologically accurate number of simulated cells in the 2D ABM based on available experimental data has been a challenge in our model-building process. Data describing cell counts are available from both histological cross-sections of radius r and with a finite thickness t (typically five to ten micrometers), and flow cytometry measurements obtained from cylindrical muscle biopsies (of radius r and length h) (Figure 6). Histological cross-sections of muscle provide cell counts per area, or volume if the cross-section thickness t is considered, and analysis of adjacent histological sections (numbering 1 through n) can be performed to obtain cell counts throughout a volume of tissue equal to V = πr²tn. However, cell counts based on this method are likely to overestimate the actual number of cells in a given volume of muscle because individual cells may be counted more than once if they traverse more than one adjacent histological section. The extent of overestimation increases as cell diameters increase and as the thickness of the histological cross-sections decrease. The smaller the cells and the thicker the sections, the less likely it is that cells in adjacent sections will get double counted. However, microscopic image quality diminishes thereby reducing one’s ability to accurately count cells as the thickness of the histological cross-section increases.

Conversely, cell counts derived from flow cytometry data obtained from muscle biopsies (of volume V = πr²h, where h is the length of the biopsy) are likely to underestimate the actual number of cells in the tissue due to loss of cells during each step in the sequential processes of tissue homogenization to liberate the cells, immunostaining, and flow cytometry. Given that one data type likely overestimates cell numbers and the other data type likely underestimates cell numbers, it is important to consider this discrepancy in data types.

4.1. 2D-to-3D scaling for a cylindrical object

In the ABM representing muscle fibers, skeletal muscle is modeled in 2D by considering a cross-sectional slice. To scale this data to a 3D section of muscle tissue, one need only determine the height of the cross-sectional slice and multiply the cell counts accordingly. If the height of the cross-sectional slice is Δz and the height of the 3D section of muscle tissue is h, then 2D cell counts can be scaled to 3D by multiplying by the scaling factor h/Δz. This assumes that cells are uniformly distributed in the z-direction (but makes no assumption about the distribution of cells in the cross-section). In general, however, if the cell distribution is non-uniform but is known as a function of z, the scaling factor can be adjusted accordingly. Since the scaling factor is independent of the radius, there is no need to consider different annuli as was done in the spherical case.

To demonstrate this, we consider the case of uniformly and randomly distributed cells in a cylinder. Cells are placed using the built-in random number generator rand in Matlab. We test the scaling method in a way analogous to the spherical case:

1. Randomly populate a 3D cylinder of radius r and height h with a specified number of cells.

2. Take a cross-section of height Δz from the cylinder. Without loss of generality, we choose to take the cross-section at height z = h/2. Project this cross-section to a 2D object.

3. Count the number of cells in the 2D object and multiply by the scaling factor h/Δz. Compare this result with the original number of cells.

4. Repeat steps (1)–(3) N times using different seeds for the random placement of cells.

For our numerical experiments, we use r = 1, h = 2, and Δz = h/100. In practice, r will be determined by the width of the simulated muscle tissue, h will be determined by the length of muscle tissue that is measured in experiments, and Δz should be chosen to be close to the diameter of a single cell in order to minimize the risk of over- or under-estimation. The results of our numerical experiments are shown in Table 3. We see that the mean scaled estimates are very close to the true number of cells in the 3D cylinder, with a mean error of less than 1%

Table 3.

Results for applying the scaling procedure to a cylindrical object, given as mean ± standard deviation. For each experiment, N = 30 replicates were performed.

# of cells in cylinder	# of cells in cross-section	Scaled estimate
100,000	1,003 ± 31	100,257 ± 3,145
200,000	2,003 ± 50	200,270 ± 4,996

5. Discussion

The more accurate mathematical and computation models are at representing the biology, the more useful they become to experimental biologists. In this brief work we show more accurate methods than have previously been used for comparing output from ABMs developed in 2D with datasets from 3D biological structures. This allows for calibration and validation of 2D computational models, which are much less expensive than 3D models, using experimental data. While in this work we have explored the relationship of 3D data to 2D models, we have not discussed the biological accuracy of these models. There is a concern that in abstracting a 3D biological system to a 2D mathematical/computational model, biological relevance may be lost. Previously we have explored this in two separate agent-based model systems and found that the validity of the models depends on the questions being asked (4; 6). We found that dimension reduction significantly affects issues of cell movement/tracking (4) and cell crowding (6) due to spatial constraints. This makes sense as there are more possibilities for agent movement direction in a 3D system than in a 2D system. Clearly, more work is needed for assessment of the relevance of 2D models for 3D biological systems.

In the context of granulomas, experimental data may include bacterial colony forming unit (CFU) counts and cell counts for various lymphocytes and phagocytes from multiple granulomas and multiple non-human primates. Since the scaling can be performed at any time during simulation, it also allows us to predict 3D cell counts for the same granuloma at multiple time points. This is not yet possible to do experimentally, since current data collection techniques are destructive. Our scaling procedure can also help validate new 3D versions of a model by comparing model output with scaled output from a previously established 2D version, which we have recently done (6).

In the demonstration of our method we have focused on structures that are spherical or cylindrical; however, with slight variations, these methods can be altered for use with biological structures that are of different, but regular, shapes. If the biological structure is irregular, it may be possible to partition the object into regular shapes so that this method can be applied piecewise. It should be noted that in our numerical tests, we consider only whole cells since cells are represented by points; there are no partial cells. In both examples and many others, the methods of data collection should also be considered, as they may over- or under-estimate true cell counts. Improvements to experimental protocols will also provide more reliable data for comparison with both 2D and 3D model systems.

Fig. 3. Test cases for testing the scaling method.

Cross-sectional slices of the two test cases: (A) a sphere, and (B) a spherical shell surrounding a much smaller sphere.

Fig. 5. Upper and lower bounds for a granuloma boundary.

Blue squares represent grid compartments containing cells in the granuloma and black squares represent grid compartments containing cells outside the granuloma. White space indicates empty grid compartments. A circle of the minimum radius r_ℓ is shown in red, and a circle of the maximum radius r_u is shown in magenta.