Fig. 3. Characterization of the anti-Stokes GeV-based nanothermometer.

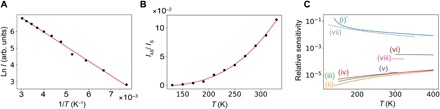
(A) Temperature dependence of the PL intensity signal upon anti-Stokes excitation (637-nm wavelength). The PL intensity was measured by monitoring the GeV’s ZPL (605 nm) isolated with a band-pass filter. The data fit well the Arrhenius-type equation $\mathit{A}{\mathit{e}}^{-({\mathit{E}}_{\mathrm{a}}/{\mathit{k}}_{\mathrm{B}}\mathit{T})}$, where the activation energy E_a = 102.96 meV is fixed to coincide with the difference in energy between the excitation laser and the GeV’s ZPL. (B) Plot of the anti-Stokes to Stokes PL ratio as a function of temperature. The ratio fits an exponential curve: $\mathit{a}+\mathit{b}{\mathit{e}}^{-[\mathit{c}/(\mathit{T}-{\mathit{T}}_0)]}$, granting the method an extremely high sensitivity. The error bars of plots in (A) and (B) are represented as vertical blue bars and are mostly equivalent to or smaller than the size of the data points. (C) Relative sensitivity plotted versus temperature for several different systems: our I_AS/I_S|_GeV measurement (i)*, the frequency shift of the GeV ZPL in our Stokes PL spectra (ii), the equivalent measurement from the literature (iii), the ZPL wavelength shift of the SnV (iv) and of the SiV center (v), the intensity of the NV ZPL (vi), the Raman I_AS/I_S ratio achieved for a bulk thermometer (vii), and the spectral shift of quantum dots (viii). The literature data are plotted over the entire temperature range demonstrated in each paper. The excitation wavelength used in (A) is 637 nm. The Stokes/anti-Stokes excitation wavelengths used in (B) are 532/637 nm.