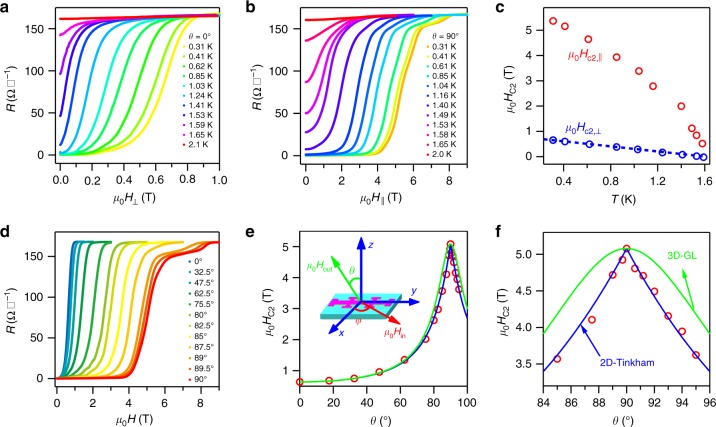
Fig. 2.

Two-dimensional superconductivity in few-layer 1T_d-MoTe₂ crystals. a, b Superconducting resistive transition of the 8.6-nm-thick MoTe₂ crystal in perpendicular magnetic field (a) and in parallel magnetic field (b). c Temperature dependence of the upper critical field μ₀H_c2 corresponding to reduced resistance r = 0.5, with magnetic field directions parallel (${\mu }_0{H}_{\mathrm{c}2,\parallel }$) and perpendicular (${\mu }_0{H}_{\mathrm{c}2,\perp }$) to the crystal plane. The dashed line is fitting to the 2D Ginzburg–Landau theory. d Magnetic field dependence of the sheet resistance of the 8.6-nm MoTe₂ device at T = 0.3 K with different tilted angles θ. e Angular dependence of the upper critical field μ₀H_c2. The solid lines represent the fitting with the 2D Tinkham formula $∣\frac{H_{\mathrm{c}2}\left(\theta \right)cos\theta }{H_{\mathrm{c}2,\perp }}∣+{\left(\frac{H_{\mathrm{c}2}\left(\theta \right)sin\theta }{H_{\mathrm{c}2,\parallel }}\right)}^2=1$ (blue line) and the 3D anisotropic mass model (3D-GL) ${\left(\frac{H_{c2}\left(\theta \right)cos\theta }{H_{\mathrm{c}2,\perp }}\right)}^2+{\left(\frac{H_{c2}\left(\theta \right)sin\theta }{H_{\mathrm{c}2,\parallel }}\right)}^2=1$ (green line), respectively. The inset is a schematic drawing of the tilt experiment setup, where x, y, and z represents the crystallographic b-, a-, and c-axis, θ is the out-of-plane tilted angle between the out-of-plane magnetic field B_out and the positive direction of z-axis, and φ is the in-plane tilted angle between the in-plane magnetic field B_in and the positive direction of y-axis. f Zoom-in view of the region around θ = 90º