Atomic Structural Models of Fibrin Oligomers

SUMMARY

The space-filling fibrin network is a major part of clots and thrombi formed in blood. Fibrin polymerization starts when fibrinogen, a plasma protein, is proteolytically converted to fibrin, which self-assembles to form double-stranded protofibrils. When reaching a critical length, these intermediate species aggregate laterally to transform into fibers arranged into branched fibrin network. We combined multiscale modeling in silico with atomic force microscopy (AFM) imaging to reconstruct complete atomic models of double-stranded fibrin protofibrils with γ- γ crosslinking, A:a and B:b knob-hole bonds, and αC regions—all important structural determinants not resolved crystallographically. Structures of fibrin oligomers and protofibrils containing up to 19 monomers were successfully validated by quantitative comparison with high-resolution AFM images. We characterized the protofibril twisting, bending, kinking, and reversibility of A:a knob-hole bonds, and calculated hydrodynamic parameters of fibrin oligomers. Atomic structures of protofibrils provide a basis to understand mechanisms of early stages of fibrin polymerization.

Graphical Abstract

In Brief

Zhmurov et al. used 27 relevant crystal structures to computationally reconstruct the full-atomic models of fibrin oligomers and protofibrils, which correlate with high-resolution atomic force microscopy images. The structures contain much valuable information for understanding the early stages of fibrin polymerization.

INTRODUCTION

Fibrin is an end product of blood clotting that forms the scaffold of hemostatic clots and obstructive thrombi in blood vessels. Fibrin is also a major component of the extracellular matrix and is involved in a broad range of cellular processes, including cell adhesion, migration, proliferation and differentiation, wound healing, angiogenesis, and inflammation (Weisel and Litvinov, 2017; Litvinov and Weisel, 2017). Fibrin is widely used as a versatile biomaterial in a variety of applications, such as hemostatic sealants, tissue engineering, as a delivery vehicle for cells, drugs, growth factors, and genes, and matrices for cell culturing (Janmey et al., 2009; Radosevich et al., 1997). Because of the fundamental biological and medical importance, molecular mechanisms of fibrin formation as well as fibrin structure and properties continue to be major areas of research (Weisel and Litvinov, 2013, 2017; Litvinov and Weisel, 2016).

Fibrin formation is initiated by the cleavage of fibrinopeptides A and B from the N termini of Aα and Bβ chains of fibrinogen, respectively, to produce fibrin monomer. The release of fibrinopeptides A exposes an N-terminal α-chain motif GPR, called knob ‘‘A’’, which binds to constitutively exposed hole ‘‘a’’ in the γ nodule of another fibrin molecule (Everse et al., 1998; Kostelansky et al., 2002), resulting in the formation of an A-a knob-hole non-covalent bond (Litvinov et al., 2005). Exposure of knobs ‘‘A’’ is necessary and sufficient to form fibrin through the interaction with holes ‘‘a.’’ The release of fibrinopeptides B exposes an N-terminal β-chain motif GHRP, called knob ‘‘B’’, which is complementary to hole ‘‘b’’ located in the b nodule of another fibrin molecule.

Fibrin polymerization begins when two monomeric fibrin molecules interact in a half-staggered fashion through the A-a knob-hole interaction. The addition of a third molecule is accompanied by an end-to-end association where, in addition to the A-a knob-hole interactions, the globular D regions of two adjacent molecules form the D:D interface. The D:D interface provides a junction between the monomers in one of the two strands in a fibrin trimer. Furthermore, fibrin monomers add longitudinally via the inter-strand A-a knob-hole bond formation and intra-strand D-D interactions to form fibrin oligomers. This growth continues until the fibrin oligomers reach the critical length of protofibrils: oligomers made of ~20–25 fibrin monomers. Fibrin protofibrils self-associate laterally to form twisted fibers of variable thickness. These branches form a three-dimensional fibrin network called a clot (Weisel and Litvinov, 2017).

The monomeric fibrin is essentially identical in structure and composition to fibrinogen except for small fibrinopeptides A and B, which are cleaved when fibrinogen is converted to fibrin, and αC domains, which are bound to the central nodule in fibrinogen but detached in fibrin (Medved et al., 2001). Therefore, fibrin oligomers and protofibrils can be reconstructed using resolved crystal structures of the human fibrinogen molecule and parts of fibrinogen and fibrin molecules, including the fibrinogen fragment D and the double-D fragment from crosslinked fibrin (see Table S1). Yet using the crystal structures of fibrinogen or fibrin [together denoted as fibrin(ogen)] is challenging. First, the crystallographic data available are incomplete. There are several flexible unstructured portions that are not resolved crystallographically yet are essential for fibrin formation, including residues 1–26 and 1–57 at the N-termini of the Aα and Bβ chains, respectively, and residues 201–610, 459–461, and 395–411 at the C-termini of the Aα, Bβ, and γ chains, respectively (Kollman et al., 2009). Second, a manifold of possible spatial arrangements of fibrin monomers when forming a protofibril makes in silico reconstruction of fibrin protofibril difficult. Third, the large system size requires using vast computational resources: a 0.5- to 0.6-μm-long protofibril made of 20 fibrin monomers contains ~60,000 amino acids, which corresponds to ~10⁶ atoms.

Determination of atomic structures of fibrin oligomers cannot be accomplished by X-ray crystallography and/or electron microscopy, owing to the unstable nature of these heterogeneous intermediate supramolecular assemblies and their characteristic elongated shape. Yet atomic-level information about these structures is necessary to elucidate the mechanisms of formation and properties of fibrin polymers, which provide the three-dimensional scaffold necessary to maintain the integrity and viscoelasticity of blood clots and thrombi. Here we employed multiscale modeling to computationally reconstitute the atomic structures of double-stranded fibrin oligomers of varying length. The atomic structural models were successfully validated using high-resolution atomic force microscopy (AFM) imaging of fibrin oligomers.

We employed the molecular dynamics (MD) simulations of atomic structural models (Brooks et al., 2009; Zhmurov et al., 2012) and C_α-based self-organized polymer (SOP) models of fibrin(ogen) and its fragments (Hyeon et al., 2006), accelerated on graphics processing units (GPUs) (Zhmurov et al., 2010a, 2010b; 2011; Alekseenko et al., 2016), to perform a step-by-step reconstruction of a complete atomic structure of a 19-monomer-long fibrin protofibril using the recently published structure of a short fibrin oligomer (Zhmurov et al., 2016). The protofibril structure has interesting properties, such as twisting, bending, and kinking, and the presence of free knobs ‘‘B’’ necessary for formation of additional intra- and inter-protofibril bonds. The models obtained enabled us to explore the dynamic structural transitions in fibrin protofibrils and to predict experimentally unavailable dynamic characteristics of fibrin oligomers and protofibrils, including density, radius of gyration, diffusion coefficient, and intrinsic viscosity.

RESULTS

Stepwise Reconstruction of Fibrin Oligomers and Protofibril

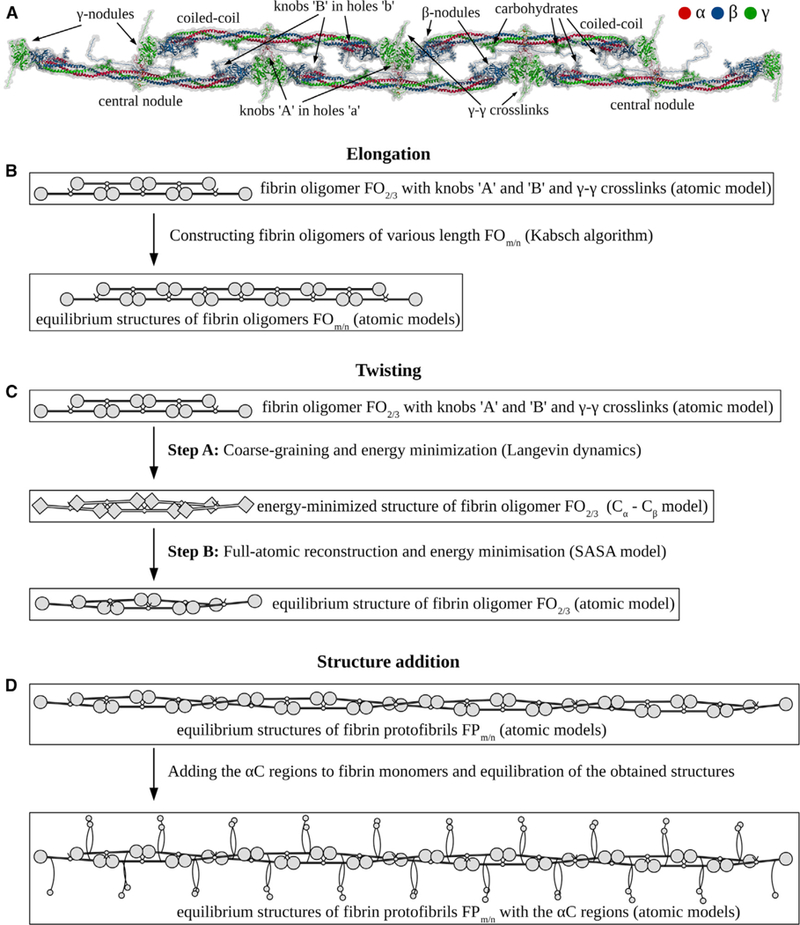
As a building block, we used the structure of short double- stranded fibrin oligomer FO_2/3 with two fibrin monomers in the first and three monomers in the second strands (Figure 1A). Using this structure, we performed stepwise elongation to create longer oligomers up to the length of a protofibril. The full-atomic model of FO_2/3 was constructed computationally in our previous study (Zhmurov et al., 2016) using all 27 relevant crystal structures of fibrinogen and its fragments resolved to date (Table S1). The structure of FO_2/3 showed good agreement with high-resolution AFM images (Zhmurov et al., 2016). In this work, we took the next step to elongate several-fold the known structure of FO_2/3 in order to reconstruct longer fibrin oligomers FO_m/n (m/n is the number of fibrin monomers in the first/second strand). This enabled us to recreate short fibrin oligomers from FO_2/3 to FO_5/6. A mere replication of the FO_2/3 structure along the longitudinal axis has resulted in formation of elongated oligomers and protofibrils that do not show any twisting detected in experimental AFM and electron microscopy images (Weisel et al., 1987; Medved et al., 1990; Protopopova et al., 2015; Huang et al., 2014). To overcome this problem, we designed an approach that uses two main crystal structures of the D:D junction. These structures correspond to the straight conformation (PDB: 1N86) of the D:D interface, used to recreate shorter fibrin oligomers, and the bent conformation (PDB: 1FZG) of the D:D interface, which we used to recreate longer oligomers (and a protofibril). To recreate twisted structures, we align two FO_2/3 constructs using the straight conformation of D-D junctions and then gradually switch to the bent conformation of the D:D junction (STAR Methods). This builds in the desired twist in the fibrin strands, in full agreement with AFM and electron microscopy experiments (Protopopova et al., 2015; Weisel et al., 1987).

Figure 1.

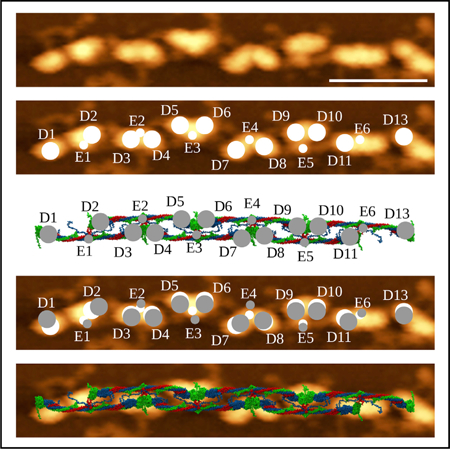
From Fibrin Oligomer to Fibrin Protofibril Based on Computational Crystallomics (A) Structure of short fibrin oligomer FO_2/3 used as an elementary building block, which contains five fibrin monomers (Zhmurov et al., 2016). (B) Schematic of elongation procedure used to reconstruct longer oligomers FO_m/n starting from short oligomers FO_2/3 as described in the text (Results; see also STAR Methods and Figure S1). (C) Workflow involved in introducing the twist into the structure of fibrin oligomers and protofibril as described in the text (Results; see also STAR Methods). (D) Final stage of protofibril reconstruction, in which all steric clashes are removed and the αC chains are incorporated (Results; see also STAR Methods).

A step-by-step reconstruction of short fibrin oligomers (FO_m/n) is illustrated in Figure 1B (elongation step with the straight conformation of D:D interface). Reconstruction of longer fibrin oligomers and protofibril (FP_9/10) is illustrated in Figure 1C (a procedure to introduce a twist; bent conformation of D:D interface; see also STAR Methods for more details). In step A of the twisting procedure, coarse-graining of FO_2/3 is performed (diamonds in Figure 1B) and Langevin simulations of the C_α-based representation of FO_2/3 is carried out to switch from the straight to the bent configuration of the D:D interfaces. In step B of the twisting procedure, the obtained conformation of FO_2/3 is back-mapped and energy-minimized using the all-atom solvent-accessible surface area model of implicit solvation. Next, we perform the elongation procedure. The atomic model of FO_2/3 with knobs ‘‘A’’ and ‘‘B’’ is replicated to reconstruct fibrin oligomers (FO_n/m) of the desired length. In the last structure-addition step, the αC regions are incorporated into each fibrin monomer, and the covalent γ-γ crosslinks between residues γ398 and γ406 of abutted fibrin monomers are introduced (Rosenfeld et al., 2015). The final structures of double-stranded fibrin polymers from the structure-addition step (Table 1) were energy-minimized to exclude possible steric clashes.

Table 1.

Molecular Parameters of Fibrin Monomer, Oligomers FO_n/m, and Protofibril FP_9/10 Calculated Based on the Atomic Models Reconstructed In Silico with and without the αC Regions: Molar Mass (M), Radius of Gyration (R_g), Diffusion Coefficient (D), Density (ρ), and Intrinsic Viscosity (η)

Constructs	M (G/mol)	Rg (nm)	D (cm2/s)	ρ (g/cm3)	η (cm3/g)
Fibrin(ogen) monomers
Truncated des-αC fibrin monomer	246,395	12.5 ± 2.0	(2.5 ± 0.3) × 10−7	1.361	24 ± 9
Full-length fibrin monomer	332,418	12.7 ± 1.3	(1.9 ± 0.2) × 10−7	1.328	38 ± 19
Double-stranded fibrin oligomers/protofibril without the αC regions
FO½	739,185	12.5 ± 2.0	(1.4 ± 0.1) × 10−7	1.350	42 ± 12
FO¾	1,724,765	19.6 ± 2.1	(8.1 ± 0.4) × 10−8	1.352	114 ± 18
FO5/6	2,710,345	41.6 ± 2.2	(6.0 ± 0.3) × 10−8	1.346	209 ± 29
FO7/8	3,695,925	67.5 ± 2.1	(4.79 ± 0.08) × 10−8	1.344	344 ± 19
FP9/10	4,681,505	117.1 ± 2.0	(4.0 ± 0.1) × 10−8	1.342	483 ± 42
Double-stranded fibrin oligomers/protofibril with the αC regions
FO½	997,254	20.1 ± 1.9	(1.14 ± 0.04) × 10−7	1.326	50 ± 7
FO¾	2,326,926	41.8 ± 2.4	(6.8 ± 0.2) × 10−8	1.325	113 ± 17
FO5/6	3,656,598	67.5 ± 2.0	(5.1 ± 0.1) × 10−8	1.325	204 ± 12
FO7/8	4,986,270	93.0 ± 1.7	(4.15 ± 0.07) × 10−8	1.324	309 ± 14
FP9/10	6,315,942	116.8 ± 1.9	(3.4 ± 0.2) × 10+	1.324	450 ± 27

The values of R_g, D, ρ, and η are for 20°C.

Atomic Structures and AFM Images of Fibrin Oligomers and Protofibrils

To compare in silico structures with AFM images, we employed the computational Monte Carlo procedure, which overlaps the positions of the centers of mass of D and E regions in the atomic structural model and in AFM images (see STAR Methods and Figure 2B). To quantify the agreement between AFM images and atomic models, we monitored the dynamics of total root-mean-square deviation (RMSD) in Monte Carlo runs. The trajectories in Figure 2C show a great reduction in RMSD values to 0.9–2 nm depending on the oligomer length.

Figure 2.

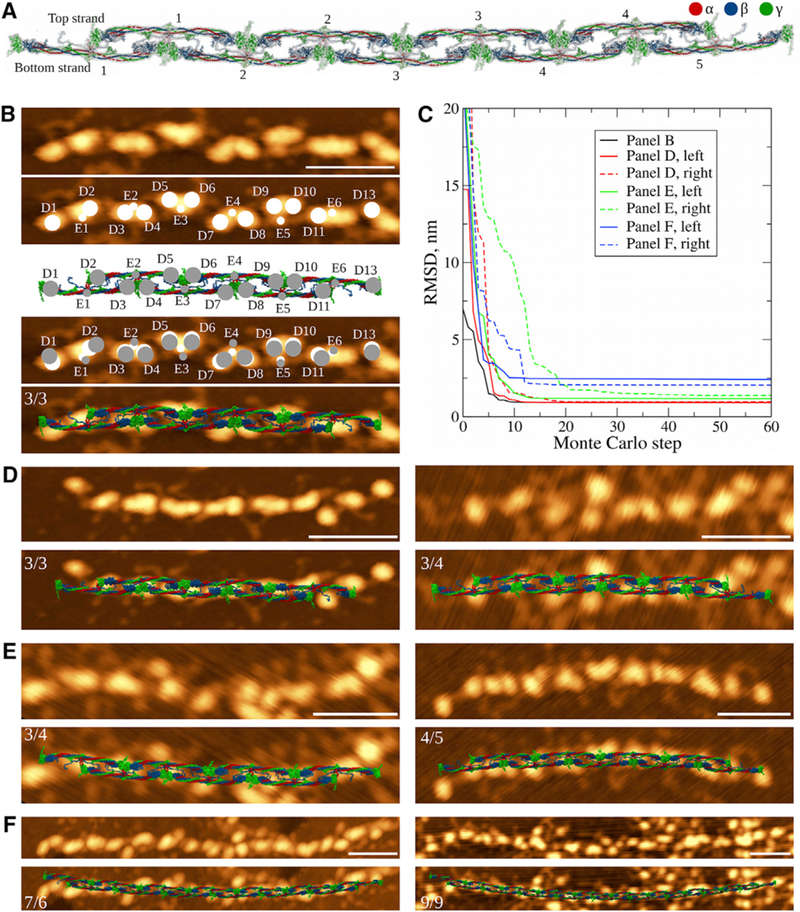
Comparison of Fibrin Oligomer Structures Obtained In Silico and In Vitro (A) Structure of double-stranded fibrin oligomer FO_4/5, obtaining using an elongation procedure (Figure 1B) applied to a short fibrin oligomer FO_2/3 with the straight conformation of D:D self-association interface (STAR Methods). (B) Monte Carlo method used to overlap the atomic structural models with AFM images. We identify the positions of geometric centers of the globular D and E regions in an AFM image (white circles) and centers of mass of these regions in the atomic structure of equal length (gray circles). Monte Carlo simulations are used to perform rigid-body transformation that minimizes the RMSD between positions of the globular regions (fourth image). Similar transformation is then applied to the atomic structure (last image). (C) Dynamics of RMSD values between the globular regions identified in AFM images and atomic structural models from Monte Carlo simulations. Shown are curves for the structure overlaps presented in (B), (D), (E), and (F). (D–F) Structures of the fibrin oligomers of various length overlaid with the AFM images. Short oligomers (D) show very good agreement with the experimental AFM data. With increasing length of fibrin oligomers reconstructed using the straight conformation of the D:D interface, the agreement becomes worse (E), and structures of longer oligomers (FO_5/6 or longer) come short at explaining the overall shape and structural features observed experimentally (F). On each AFM image the numerals indicate the number of fibrin monomers in the upper/lower strands. Scale bars, 50 nm.

We first recreated atomic models of short fibrin oligomers by applying the elongation procedure (Figure 1B) to the initial structure of FO_2/3, to reconstruct the structures up to nine monomers long (FO4/5, Figure 2A). We correlated these structures with their high-resolution AFM images for short oligomers containing up to nine fibrin monomers (FO_4/5; Table 1). In AFM imaging, short fibrin oligomers appear as elongated constructs with regularly spaced heart-shaped nodules and two adjacent nodules facing in opposite directions (Figure 2). Each of these nodules corresponds to a single D-E-D trinodular unit. The derived atomic structures and AFM images for short fibrin oligomers are compared in Figures 2B and 2D, which show good agreement between the structures obtained experimentally and computationally. Next, we turned to reconstruction of longer oligomers (FO_5/6 and longer) up to a protofibril FP_9/10. We elongated oligomer FO_4/5 with FO_2/3 using the elongation procedure described in the STAR Methods (Figure 1B). The structures obtained in silico did not compare well with their corresponding AFM images (Figures 2E and 3F), which could be due to protofibril twisting not present in the modeled structures. Quantitatively, this is reflected in higher values of RMSD for longer structures (0.9–1.0 nm for short oligomer FO_3/3 versus 1.8–2.0 nm for long oligomer FO_6/7; see Figure 2C). Next, we elongated short oligomers up to the length of a fibrin protofibril FP_9/10 (Figure 3A and Table 1). At this length scale, the structure of FP_9/10 obtained with the straight conformation of D:D interface did not capture the helical twist observed in AFM images (Figures 2E, 2F, and 3D). Using the structure of FP_9/10 obtained computationally, we calculated the helical radius and helical pitch, which came to 650 nm and 3,300 nm, respectively. This is a straight structure on the protofibril length scale of ~500 nm.

Figure 3.

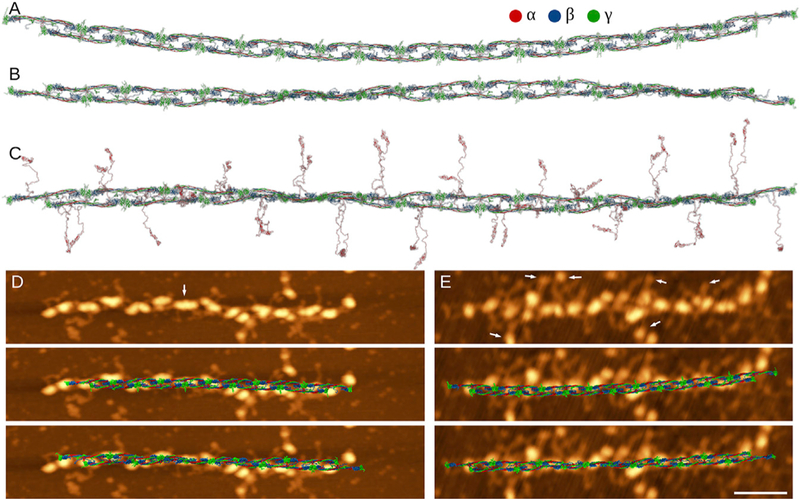
Comparison of Structures of Fibrin Protofibril FP_9/10 Obtained In Silico and In Vitro (A) Atomic model of FP_9/10 with a straight conformation of D:D interface (PDB: 1N86) obtained using the elongation procedure (Figure 1B). (B) Atomic model of FP_9/10 with a twisted conformation of D:D interface (PDB: 1FZG) obtained using the twisting procedure followed by the elongation step (Figures 1C and 1B). This structure was equilibrated using Langevin simulations of the SOP model of FP_9/10, then back-mapped and energy-minimized in the full-atomic representation (see also Figure S2). (C) Energy-minimized structure of FP_9/10 as in (B) but with the αC regions (structure-addition step in Figure 1C). See also Data S1 and S2. (D and E) Atomic models of fibrin protofibril backbones (shown without the αC regions for clarity) of different size and shape (straight and bent conformations) reconstructed in silico are overlaid with the high-resolution AFM images of fibrin protofibrils. The white arrow in (D) indicates the position along the oligomer where the trinodular structure of D-E-D construct is not visible, which suggests twisting of the structure. The arrows in (E) show the position of αC domains. Scale bar, 50 nm.

To build in a twist in fibrin oligomers and protofibrils, we first applied the twisting procedure (Figure 1C) and then the elongation procedure (Figure 1B). The equilibrium structure obtained shows that the transition from the straight to the bent double-D conformation with the twisting procedure results in an overall shape change of FP_9/10 from the parallel double-stranded (Figure 3A) to the twisted (double-stranded) helical form (Figure 3B). Transient structures of FP_9/10 populated in the course D:D interface remodeling are displayed in Figure S2 (see Video S1). As the protofibril FP_9/10 twists, the helical radius and helical pitch decreases, respectively, from 650 nm to 5 nm and from 3,300 nm to 400 nm (see Figure S2 and Video S1), as a result of dynamic remodeling of all D:E:D interfaces reinforcing the protofibril’s structure. The comparison of atomic structures and AFM images of longer fibrin oligomers showed better agreement (Figure 3D). Note that the average values for RMSD are slightly lower for twisted structures (1.2 ± 0.3 nm; sample size = 30) compared with straight oligomers (1.4 ± 0.4 nm; sample size = 30).

Complete Structure of a Fibrin Protofibril with the αC Regions

The C-terminal part of fibrinogen’s Aα chain, called the αC region (residues Aα221–610), consists of the proline-rich unstructured αC connector (Aα221–390) and the relatively compact αC domain (Aα391–610) (Tsurupa et al., 2009). The αC region is missing in all the crystal structures of fibrinogen and its fragments resolved to date. The structure of bovine fibrinogen’s αC domain was partially resolved by nuclear magnetic resonance (Burton et al., 2007), yet the structure of human fibrinogen’s αC domain is not known (Tsurupa et al., 2009). We recreated this structure using sequence homology between the human and bovine fibrin(ogen) with the Modeller software suite (Webb and Šali, 2017). Structure snapshots of the αC domain randomly selected from independent MD runs showed a double β hairpin stabilized by the S-S bond. The αC-domains can be separated into the N-terminal and C-terminal subdomains as suggested earlier (Tsurupa et al., 2009, 2012). Since αC connectors are not resolved by the X-ray crystallography, they do not possess stable secondary or tertiary structure. Therefore, the incorporation of αC connectors in a random coil conformation does not lead to any structural artifacts. In a structure-addition procedure (Figure 1D), we incorporated the missing C-terminal portions of the α connector in a random conformation to arrive at the complete atomic structure of a fibrin protofibril FP_9/10 (Figure 3C).

We compared the full-atomic structure of FP_9/10 containing αC regions with the AFM images (Figure 3). The protofibril’s shape and positions of the αC regions in the atomic model and AFM images of FP_9/10 agreed well. The αC regions were predominantly perpendicular to the protofibril axis. Although the αC regions were occasionally interconnected, they were mostly single. Not all αC regions were seen in AFM images (assuming two αC regions per monomer), and we identified on average 1.6 αC regions per monomer. Some of the αC regions might have been proteolytically truncated in the fibrinogen purified from plasma or have been adsorbed at positions not clearly visible on the surface (e.g., under the protofibril backbone).

Conformational Dynamics of the Fibrin Protofibril Chain

From experimental AFM images, the average contour length of fibrin protofibrils is 213 ± 101 nm and the average end-to-end distance is 197 ± 86 nm (n = 30). This gives an average end-to-end to contour length ratio of 0.94 ± 0.09 (n = 30), which shows that protofibrils are bent. Since our in silico structures were recreated based on the X-ray data, they lack this conformational flexibility. To explore dynamic transitions in the protofibril structure, we performed MD simulations using the obtained structure of FP_9/10 (see STAR Methods and Video S2), which revealed significant structural alterations including bending (Figure 4A) and kinking (Figure 4B). This agrees well with the previously published experimental data (Protopopova et al., 2015, 2017; Huang et al., 2014; Chernysh et al., 2011; Medved et al., 1990; Hunziker et al., 1988; Fowler et al., 1981) and with our AFM images (Figure 4).

Figure 4.

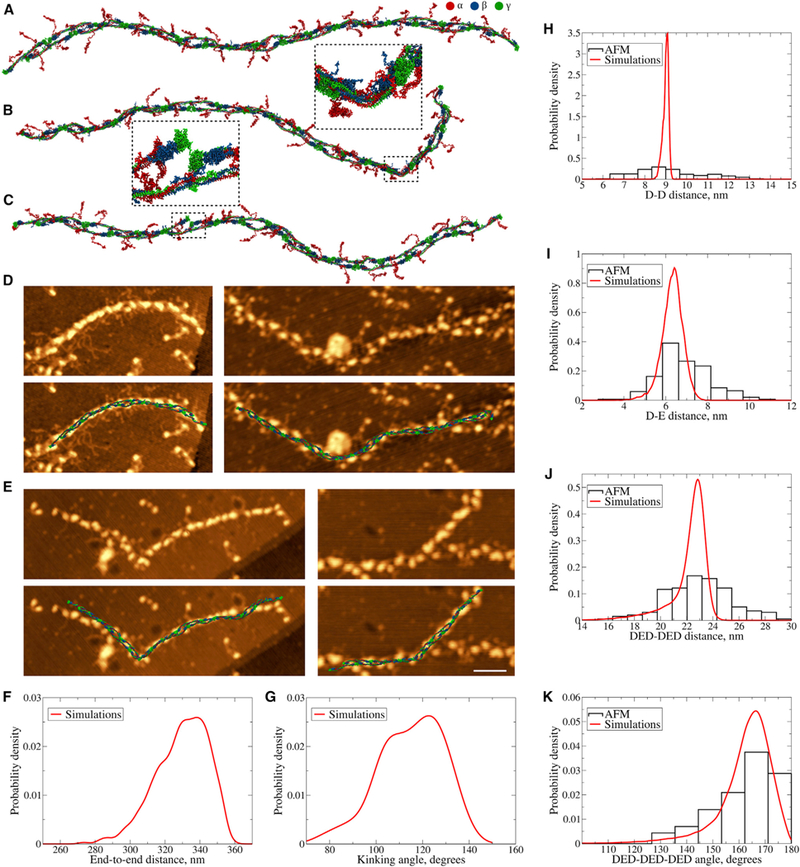
Conformational Dynamics of Fibrin Protofibrils (A) Structure of FP_9/10 in a coarse-grained representation used to study the equilibrium dynamics of fibril protofibrils. (B) Structure showing a kink formed in the unstructured regions of α-helical coiled coils in both strands (magnified in the inset). (C) Structure with dissociated A:a knob-hole bond. The A:a knob-hole bond dissociation is followed by the disruption of D:D self-association interface (magnified in the inset). (D and E) Representative high-resolution AFM images of bent fibrin protofibrils (D) and protofibrils with kinks (E) overlaid with the corresponding structures obtained in silico. Scale bar, 50 nm. (F and G) Probability distributions of the end-to-end distances (F, sample size = 1,000) and kinking angles (G, sample size = 51) from equilibrium simulations of fibrin protofibrils obtained using kernel density estimation with the Gaussian kernel (Bura et al., 2009). (H–K) Probability distributions of the distances between two adjacent D regions (H, sample size = 153 for AFM and 100,000 for simulations), between D and E regions in the DED complex (I, sample sizes = 200 and 200,000), between two consecutive DED complexes (J, sample sizes = 173 and 92,000), and probability distributions of angles made by three consecutive DED complexes (K, sample sizes = 129 and 67,000) from AFM experiments (histograms) and equilibrium MD simulations (curves). Theoretical distributions were obtained using kernel density estimation with the Gaussian kernel (Bura et al., 2009). See also Table S2.

The distribution of end-to-end distances (i.e., the distances between centers of the end D:E:D complexes) in FP_9/10 from MD simulations is displayed in Figure 4F. The average end-to-end distance in FP_9/10 is R = 330 ± 15 nm. With the contour length L₀ = 403 nm (9 monomers, 44.8-nm length of monomer), the average persistence length of protofibril FP_9/10 is L_p = 320 ± 80 nm (see STAR Methods). There is a variation in experimental estimates of L_p for fibrin protofibrils, with values ranging from ~100 nm to 500 nm (Piechocka et al., 2016; Storm et al., 2005). Based on our AFM images, L_p = 420–480 nm, which is in good agreement with our simulations. The higher value of L_p observed in AFM images can be attributed to the non-covalent interactions (adsorption forces) between the protofibrils’ backbone and the surface. Reversible formation of kinks in the protofibril structure observed in our simulations was due to simultaneous bending of the coiled coils in adjacent strands around the positions identified in the previous simulation studies (Köhler et al., 2015; Figure 3). This is in agreement with AFM images, in which kinks were indeed detected (Figure 4E). Deviations of the atomic structures from the AFM images at the protofibril’s tails are due to limited sampling of the conformational space in the MD simulations. The probability distribution of kinking angles from MD simulations for FP_9/10 is shown in Figure 4G.

To quantitatively compare the AFM images and the atomic structural models, we computed the distributions of distances between adjacent D regions (Figure 4H), distribution of distances between D and E regions in DED constructs (Figure 4I), and distribution of distances between DED complexes (Figure 4J). To probe the bending rigidity of protofibrils, we computed the distributions of angles formed by three DED complexes (Figure 4K). To extract these characteristics from AFM images, we only selected protofibrils in which these fragments are visible and located their geometric centers; in the simulations, we computed the centers of mass of these fragments. The average values of all four quantities from AFM images and equilibrium MD simulations agree well (see Table S2), although SDs are larger in AFM images.

Structural Transitions in Fibrin Protofibril

Dissociation of A:a Knob-Hole Bonds

The long 10-ms MD simulations of FP_9/10 showed that the A:a knob-hole bonds dissociate. This significantly weakens the D:E:D interface, leading to disruption of the D:D junction (Figure 4C), which does not occur when the A:a knob-hole bonds are intact. The D:D junction is the weakest link in the single-stranded fibrin oligomers (Zhmurov et al., 2011, 2012). In accord with these findings, AFM images also show irregularly shaped D:E:D fragments, which suggests the D:D interface disruption (see Figures 2E, 2F, 3E, 4D, and 4E). These results point to the importance of γ-γ covalent crosslinking, which reinforces the D:D interface when fibrin protofibrils form.

αC Regions

To sample conformations of the αC regions with flexible βN regions, we performed 10-ms equilibrium MD simulations of the protofibril FP_9/10 with a constrained protofibril backbone and free knobs ‘‘B’’ (STAR Methods; see Video S3). We constructed the probability distribution of the distances between the protofibril longitudinal axis and the centers of mass of αC domains and compared it with the experimental histogram of the same quantity. Figure 5B shows that the agreement is very good, albeit the SDs are smaller in the simulations. This might be due to overstabilization of the αC domains in the simulations. The structure of the αC domain is not resolved experimentally, which suggests that it is not stable. Longer αC connectors are typically bent, which explains why the average distance between the αC regions and the protofibril backbone is only 17 nm (Figure 5B).

Figure 5.

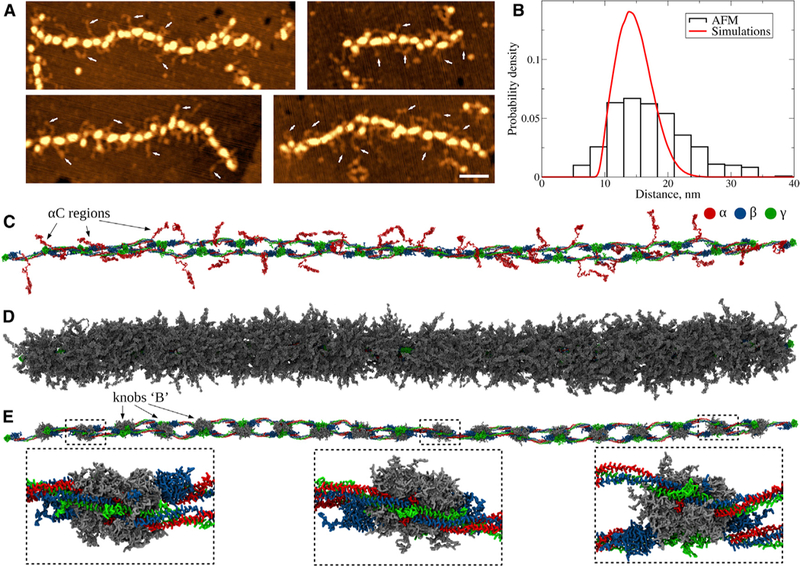
Dynamics of αC Regions and Knobs ‘‘B’’ (A) AFM images of fibrin protofibrils: the top image shows multiple αC regions protruding from the protofibril backbone (indicated by the arrows). Scale bar, 50 nm. (B) Experimental and theoretical probability distributions of the distances between the ends of αC regions and the protofibril backbone. Experimental distribution from AFM images is colored red (sample size = 410); theoretical distribution obtained using kernel density estimation with the Gaussian kernel (Bura et al., 2009) from five simulation runs is colored black (sample size = 50,000). (C) Structure of fibrin protofibrils from Langevin simulations of FP_9/10 in a coarse-grained representation with the protofibril backbone constrained. (D) Same structure as in (C) superposed with an ensemble of conformations of αC regions (shown in gray). (E) Same structure as in (D) superposed with an ensemble of conformations of knobs ‘‘B’’ (magnified in the insets).

B:b Knob-Hole Interactions

We explored the conformational transitions in the βN regions with knobs ‘‘B.’’ The GHR active sequence does not drift far away from the central nodule, making the intra-protofibril B:b highly unlikely to form (Figure 5E). This suggests that additional structural changes in the protofibril are required for the B:b knob-hole bonds to form within the protofibril, in full agreement with earlier reports (Medved et al., 2001). These transitions (B:b knob-hole bond formation) cannot be sampled in MD simulations due to the limited time span (10 ms), and there might be additional putative inter-atomic contacts that guide the βN re gions toward the holes ‘‘b.’’ There is experimental evidence suggesting that the B:b knob-hole bonds can form both between the fibrin strands inside the protofibril and between the protofibrils (Litvinov et al., 2007; Blombäck et al., 1978; Weisel, 1986). For this reason, we recreated two protofibril constructs: one with knobs ‘‘B’’ bound to holes ‘‘b,’’ and the other with free knobs ‘‘B’’; see the PDB files in Data S1 for knobs-in structure and Data S2 for knobs-out structure.

Hydrodynamic Parameters of Fibrin Oligomers and Protofibril

We calculated the (hydro)dynamic molecular characteristics for double-stranded fibrin oligomers and protofibrils (STAR Methods) and profiled them as a function of their size (Figure 6 and Table 1). First, we compared our theoretical predictions with available experimental values for some of these quantities. Very good agreement was found for the (translational) diffusion coefficient D, i.e., (1.5–2.2) × 10⁻⁷ cm²/s (experiment for full-length fibrinogen; Raynal et al., 2013) versus (2.5 ± 0.3) × 10⁻⁷ cm²/s (our simulations for truncated fibrin monomer without αC regions). Slightly lower values of D obtained for the full-length fibrin monomer can be attributed to the presence of bulky αC appendages, which are absent in truncated fibrin variants. Using confocal microscopy, Chernysh et al. (2011) estimated the diffusion coefficient (D) for 500-nm-long protofibril to be D = 3.7 × 10⁻⁸ cm²/s. This is in very good agreement with our values for FP_9/10, i.e., D = (3.4 ± 0.2) 3 10⁻⁸ cm²/s for the full-length molecules and D = (4.0 ± 0.1) × 10⁻⁸ cm²/s for those with truncated αC region (Table 1). Given these values of the diffusion coefficient the time needed for the protofibrils to travel toward one another will be fractions of a second, which is significantly shorter than overall polymerization timescale of minutes under similar conditions (Protopopova et al., 2017). Thus, the lateral aggregation of protofibrils is not limited by their diffusion.

Figure 6.

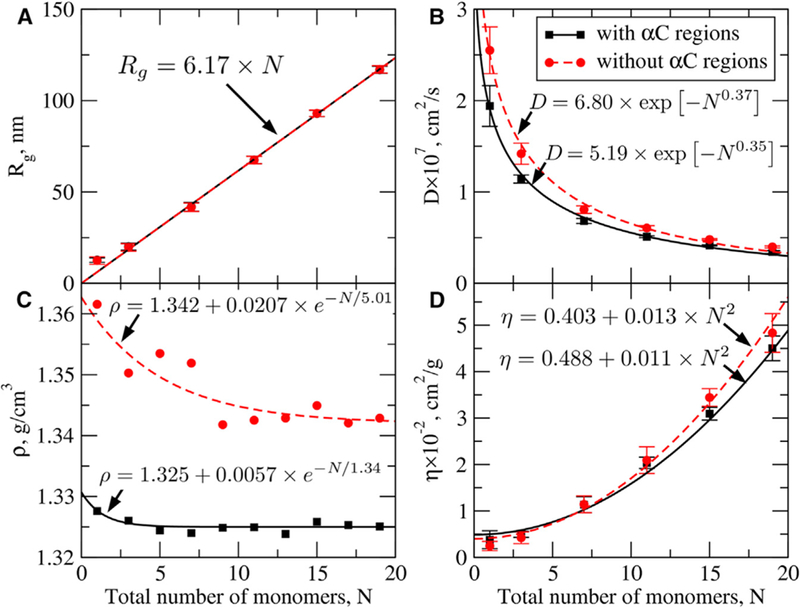
Molecular (Hydro)Dynamic Parameters for Double-Stranded Fibrin Polymers (with and without αC Regions; Based on Data in Table 1) (A–D) Shown are the profiles of the radius of gyration (R_g; A), translational diffusion coefficient (D; B), protein density (ρ; C), and intrinsic viscosity (η; D) as a function of size N = n + m (n/m are the numbers of monomers in the first/second strands). Analytical expressions approximating these quantities as functions of N (formulas) and results of numerical fitting (curves) are displayed on the graphs. We used a linear function for Rg, stretched exponential functions for D, exponential function for ρ, and quadratic function for η. Calculated values of hydrodynamic parameters (data points) are accumulated in Table 1. Data for the full-length (truncated) fibrin molecules are shown as black squares (red circles) with the solid (dashed) black (red) line for analytical fit. Error bars in (A), (B), and (D) are standard deviations.

The density of fibrin oligomers (1.34–1.36 g/cm³) was also found to be in good agreement with experiments (ρ = 1.38 g/cm³; Adamczyk et al., 2012). The density of fibrin with flexible αC regions (1.32–1.33 g/cm³) was lower than the density of fibrin without αC regions (1.34–1.36 g/cm³). Theoretical values of the intrinsic viscosity η for the truncated fibrin (24 ± 9 cm³/g) and full-length fibrin monomer (38 ± 19 cm³/g) are also within the experimental range (21–48 cm³/g; Adamczyk et al., 2012). Larger variability in the theoretical values of η for the full-length fibrinogen is due to higher extensibility of αC appendages (Table 1). This supports our findings, namely that fibrinogen in solution exists in two conformational populations: one population with a lower value of η corresponding to conformations of fibrin’s αC domains attached to the central nodule; and the other population with a higher value of η that corresponds to conformations with free αC regions (Zuev et al., 2017). The agreement between experimental and theoretical values of D, ρ, and η we have obtained for fibrin monomers and the structures we have recreated enabled us to predict the values of D, ρ, and η and radius of gyration R_g for fibrin oligomers and protofibrils not available experimentally (Table 1). We also derived analytical expressions that allow for the extrapolation of these quantities to fibrin protofibrils of arbitrary length (Figure 6).

DISCUSSION

Fibrin oligomers and protofibrils are important intermediate products formed early during fibrin polymerization. Resolution of atomic structures of fibrin oligomers and protofibrils is needed to illuminate the mechanisms of the early stages of fibrin formation, including lateral aggregation of protofibrils, and to characterize the remarkable extensibility and viscoelasticity of fibrin fibers (Liu et al., 2010; Litvinov and Weisel, 2017). Yet experimental determination of the structure and characterization of the properties of double-stranded fibrin polymers is difficult due to their elongated shape and highly unstable nature. We employed a powerful combination of the state-of-the-art experimental AFM imaging technique and theoretical approaches to multiscale modeling accelerated on a GPU to gather the atomic-level information about the structure and properties of fibrin oligomers and protofibrils. Using the full-atomic structure of a short fibrin oligomer FO_2/3 (Figure 1; Zhmurov et al., 2016), here we have reconstructed the atomic structures of longer fibrin oligomers FO_¾–FO_7/8 up to a 19-mer protofibril FP_9/10 (Figures 2 and 3; Table 1). These constructs involve γ-γ crosslinking, A:a and B:b knob-hole bonds, and αC regions—all important functional elements of fibrin—and carbohydrates. The double-stranded fibrin structures were successfully validated through the direct comparison with high-resolution AFM images of oligomers and protofibrils (Figures 2 and 3; Data S1 and S2).

Early products of fibrin polymerization are two-stranded oligomers (Fowler et al., 1981; Chernysh et al., 2011; Huang et al., 2014). A common feature of fibrin oligomers visualized with transmission electron microscopy is their twisted helical shape, although reported parameters of the oligomers’ helicity are highly variable. Medved et al. (1990) showed that some protofibrils form twisted structures with a helical pitch of ~100 nm, whereas other protofibrils are nearly straight. In agreement with this study, we found that the helical pitch decreases from 3,300 nm to 400 nm (Figure 3) following the transition from the straight conformation (PDB: 1N86) to the bent conformation (PDB: 1FZG) of the D:D interface (Figures 3A, 3B, and S2), and the helical radius decreases from 650 nm to 5 nm. This points to the important role played by the D:D interfacial flexibility in early stages of fibrin polymerization. We did not observe a helical pitch <400 nm, which might be due to the experimental conditions used in previous studies (Medved et al., 1990) or to crystal packing forces in the atomic structures used. In most experiments, fibrin protofibrils are straight and thin, which agrees with our results. After reaching a certain length, fibrin protofibrils aggregate laterally to form thick twisted fibers. Fibrin fibers have a 20- to 60-nm helical radius and ~2,000-nm helical pitch (Weisel et al., 1987), and continue to twist as they grow.

The reconstructed double-stranded fibrin oligomers and protofibrils correspond to the known ultrastructures, but surpass the available experimental data in spatial resolution. We are aware of other models of fibrin protofibrils (Yang et al., 2000; Pechik et al., 2006; Huang et al., 2014). The model proposed by Yang et al. (2000) captures the main structural features of fibrin oligomers, including the half-staggered molecular overlay formed by two fibrin strands. However, this model is ad hoc rather than systematic, and lacks a detailed analysis of the crystal forms. This model provides a static view of fibrin structure with missing γ-γ crosslinking, A:a and B:b knob-hole bonds, and αC regions. Another model (Huang et al., 2014) captures the half-staggered molecular arrangement of fibrin strands, and has a helical pitch of 90 nm. Yet a closer look reveals major steric clashes in the DED regions, which make the A-a bond formation unlikely. Also, this model is lacking γ-γ crosslinking, knob-hole bonds, and αC regions, and is based on the chicken fibrinogen structure (PDB: 1M1J).

We employed equilibrium MD simulations of fibrin protofibril FP_9/10 to explore the dynamic structural transitions that occur in double-stranded fibrin polymers. Fibrin protofibrils behave like other double-stranded biopolymers, such as double- stranded DNA, but with a longer 320-nm persistence length, and show a high degree of bending. A theoretical probability density curve shows that due to bending, the end-to-end distance in FP_9/10 decreases from ~400 nm (contour length) to ~330 nm (Figure 4F). This might be important for the fiber formation and fiber branching (Figure 4). Experimental AFM images reveal more bending flexibility than the in silico structures, and the protofibril’s bending becomes more pronounced with increasing length. We also observe reversible kinking of the protofibril backbone with the 80° to 140° kinking angle range and an average kinking angle of 115° (Figure 4G). Protofibril bending and kinking could be one of the mechanisms of initiation of branch points in growing fibrin fibers.

In the simulations, we observed the dissociation of A:a knob-hole non-covalent bonds, which was followed by the disruption of the D:E:D interface. This suggests a secondary role played by the D:D interface in fibrin polymerization, and also potentially supports the so-called Y-ladder model of fibrin fiber growth (Rocco et al., 2014). According to this model, the D:E:D interface becomes stable only after both knobs ‘‘A’’ are bound to their corresponding holes ‘‘a’’ (Rocco et al., 2014). Since upon the disruption of D:E:D interface and D-region rotation one A:a knob-hole bond is completely dissociated, a knob ‘‘A’’ and a hole ‘‘a’’ might become available for inter-protofibril cross-coupling. Another fibrin monomer from another protofibril could then bind, thus initiating a branch point. Formation of branch points is visible in some of the protofibril images (Figure 4E). We did not observe formation of new A:a knob-hole bonds in the millisecond timescale of simulations, hence this transition occurs in a longer timescale.

The length of αC connectors is very important for mechanical properties of fibrin fibers (Falvo et al., 2008). Since the αC domains are capable of interacting with each other (Tsurupa et al., 2011, 2012; Litvinov et al., 2007) and with the globular parts of fibrin molecules (Tsurupa et al., 2009), it is important that they have an optimal length. When the αC connectors are long (as in human fibrinogen) their αC domains tend to form non-covalent bonds with other αC domains within the same protofibril and between the protofibrils. When the αC connectors are short (as in chicken fibrinogen), the αC domains hardly form binding contacts between protofibrils but only within the protofibril. We see in the simulations and in AFM images that the span of the αC regions is long enough so that the αC domains can form the αC-αC contacts within the protofibril and between protofibrils (Figure 5). The experimental histogram of the lengths of αC region shows the 10- to 35-nm range and an average length of 17.3 nm; the theoretical probability density curve reveals a smaller 10- to 20-nm range and a similar average length of 14.7 nm. This large variability also explains why in AFM images were on average 1.6 αC regions per fibrin monomer (<2). Our results imply that the conformational dynamics of αC regions plays a role in defining the thickness of fibrin fibers (number of protofibrils in a fiber).

The physiological role of B:b knob-hole bonds is not yet fully understood (Weisel and Litvinov, 2017). Although knobs ‘‘B’’ are long enough to reach and bind to the corresponding holes ‘‘b’’ in the same protofibril, our simulations of FP_9/10 with free knobs ‘‘B’’ show that they have a limited span due to thermal fluctuations (Figure 5E). Hence, formation of intra-protofibril B:b contacts is possible only when Nβ regions are close to the globular parts of fibrin, interacting with γ and β nodules of adjacent molecules (Moskowitz and Budzynski, 1994). These interactions can guide the knob ‘‘B’’ to the hole ‘‘b’’ or/and to the thrombin active-site cleft (Pechik et al., 2006). Upon formation of B:b knob-hole bonds, the β nodule dissociates from the a-helical coiled coil, which results in the exposure of the tissue plasminogen activator and plasminogen binding cites in the coiled coil (Medved et al., 2001). This transition might help to bring holes ‘‘b’’ of adjacent protofibril closer to knobs ‘‘B,’’ thus facilitating the inter-protofibril contacts’ formation. Our simulations for protofibril FP_9/10 suggest that the intra-protofibril B:b contacts are less probable than the inter-protofibril B:b contacts, which also explains why the formation of fibrin fibers occurs even in the absence of knobs ‘‘B’’ (Moskowitz and Budzynski, 1994; Weisel, 1986).

We calculated the molecular hydrodynamic parameters for double-stranded fibrin oligomers and protofibrils, which are not available experimentally (Table 1), and extracted the scaling laws for R_g, D, η, and ρ as functions of their size N (number of fibrin monomers; Figure 6). The protein density ρ was found to depend on N exponentially (Figure 6C) in full agreement with the predictions made by Fischer et al. (2004). The profile of R_g shows a linear increase with N starting from 5 to 7 monomers (Figure 6A), because at larger N fibrin oligomers are pseudo-one-dimensional with size growing with N. This also explains why the intrinsic viscosity η increases quadratically with N. According to the Flory theory, $\eta =\Phi R_g{}^3/M$, where $\Phi$ is a universal constant and M is the molar mass (Doi and Edwards, 1986). Indeed, for a linear polymer $R_g\sim N$ and $M\sim N$, and so $\eta \sim N^2$ (Figure 6D).

STAR✶METHODS

CONTACT FOR REAGENT AND RESOURCE SHARING

Further information and requests for resources and reagents should be directed to and will be fulfilled by the Lead Contact, Valeri Barsegov (Valeri_Barsegov@uml.edu).

EXPERIMENTAL MODEL AND SUBJECT DETAILS

Not applicable.

METHODS DETAILS

Preparation of Fibrin Oligomers and Protofibrils

0.15 mg/ml human fibrinogen (Hyphen BioMed, France) in 20 mM Tris-HCl buffer (pH 7.4) containing 150 mM NaCl and 10 mM CaCl₂ was mixed with 0.05 U/ml thrombin (final concentration), incubated for 5 min at room temperature, and then diluted 100-fold with buffer and immediately used in AFM sample preparation.

Atomic Force Microscopy

AFM imaging was performed on the surface of modified hydrophilized graphite (Protopopova et al., 2015). 3 μl of a sample solution was applied on the modified graphite surface and kept for 15 s at room temperature. A ~50x volume drop of fresh milli-Q water was then carefully placed above the sample solution for 10 s and then removed with a flow of air making the surface ready for imaging. The AFM imaging was performed using a MFP-3D microscope (Asylum Research - Oxford Instruments, USA) in AC mode with a typical scan rate of 0.8 Hz. Images were taken in air using super-sharp cantilevers with a tip radius about 1 nm (Klinov et al., 1998). Femto-Scan software (http://www.femtoscanonline.com) was used to filter and analyze the AFM data.

Elongation Step

We recreated fibrin protofibrils FP_n/m by replicating the structure of oligomer FO_2/3. A schematic of elongation procedure is displayed in Figure S1. First, we removed two fibrin molecules from the atomic model of FO_2/3 that leaves only one half-molecule overlap (two far-most molecules in Figures 1 and S1) to obtain the structure of FO_½. Next, we aligned two copies of FO_½ so that one monomer in the upper strand of the first copy overlaps with another monomer of the second copy (Figure S1) to obtain the structure of oligomer FO_2/3. This step was repeated using fragments FO_2/3 and FO_½ placed at the growing end of fibrin polymer to obtain the structures of desired length FO_n/m.

Twisting Procedure

Step A. FO_2/3 structure refinement and energy minimization: Initial reconstruction of FO_2/3 oligomer obtained in our previous study (Zhmurov et al., 2016) was based on the PDB structure 1N86. This structure corresponds to the straight conformation of the D:D interface. We utilized the SOP-GPU package (Zhmurov et al., 2010a; 2010b) to carry out the Langevin dynamics simulations of the C_α-based SOP model of FO_2/3 with side chains to induce structural rearrangements in FO_2/3 due to the D:D interface transitioning from the straight conformation to the bent conformation. We ‘‘switched off’’ the binding interactions reinforcing the straight double-D structure 1N86 and ‘‘switched on’’ the interactions corresponding to the bent double-D structure 1FZG. We used the positions of C_α- and C_β-atoms taken from the published F_O2/3 structure (Zhmurov et al., 2016). To parameterize the SOP model of FO_2/3, we used structures 3GHG, 1N86 and 1FZG. Parameters for the knob-hole interactions were taken from the structure of fibrinogen 3GHG co-crystalized with peptides GPRP and GHRP. Step A was considered to be complete when the number of native contacts, potential energy of the polypeptide chain, helical pitch and helical radius of FO_2/3 all leveled off, attaining some constant values. Step B. Recreating the atomistic structure of fragment FO_2/3: Back-mapping of the atomic structure of FO_2/3 from its coarse-grained counterpart was achieved through the initial placement of atoms and subsequent structure refinement using energy minimization (Wassenaar et al., 2014). Next, we performed energy minimization with harmonic constraints applied to all C_α-atoms. These constraints were imposed using the C_α-atoms positions in the coarse-grained structure from Step A. Gradient descent energy minimization was used with the spring constants for constrained atoms gradually increasing from 0 to 100 pN/nm. We verified that the positions of all C_α-atoms in the full-atomic model coincide with those from the coarse-grained structure with RMSD values < 0.02 nm. The obtained structure was then energy-minimized again using the steepest descent algorithm but now without the constraints.

Structure-Addition Step

In the structures FO_n/m there are steric clashes involving atoms of the two newly placed fibrin molecules in the elongation step, there are no γ-γ crosslinks, and there are no αC-regions. In the structure-addition step, steric clashes were removed, and the γ-γ cross-links, αC-regions, and carbohydrates were incorporated into the fibrin oligomers FO_n/m and protofibril FP_9/10. The αC regions with disordered part (residues 210–391) and ordered part (residues 392–610) were recreated using the Modeller software (Webb and Šali, 2017). Energy minimization of complete structures FO_n/m and FP_9/10 was performed in the full-atomic resolution. To visualize the structural transitions in a protofibril that correspond to the transformation from the straight to the bent D:D self-association interface, we applied the elongation procedure to the initial and transient structures (see Figures 2 and S2; see also Video S1).

Comparison of the AFM Images with Atomic Structural Models

To compare the atomic structures with AFM images, we developed a procedure based on Monte Carlo simulations. First, we take an AFM image and locate geometric centers of D and E regions (white circles in Figure 2B). Next, we take an in silico structure of the same length and reduce it to the centers of mass of the D and E regions (grey circles in Figure 2B). Then, a rigid-body translation/rotation Monte Carlo step is made using the positions of the globular regions in an in silico structure. The step is accepted if the total RMSD value for distances between the globular regions in an AFM image and the atomic structure is reduced; otherwise the step is rejected. The translation/rotation amplitude is randomly selected from the 200-nm interval for translations and 180-degree interval for rotations. If 100 sequential translational/rotational steps are rejected, then the amplitude of translational-rotational steps is reduced by 5%. The Monte Carlo simulation is considered to be complete when the amplitudes for translations and rotations reach the threshold value (0.01 nm for translations and 0.01 degrees for rotations). Finally, the total translational-rotational transformation is applied to the full-atomic structure of fibrin oligomer (back-mapping; see Figure 2B). We performed a total of 20 Monte Carlo runs for each AFM image, from which we then selected the image with the lowest total RMSD. The dynamics of RMSD values for the AFM images of fibrin oligomers displayed in Figure 2 are in Figure 2C, which shows higher RMSD values for longer oligomers and lower RMSD values for twisted vs. straight oligomers (i.e. 1.2±0.3 nm vs. 1.4±0.4 nm; sample size = 30).

Conformational Dynamics of Fibrin Protofibril

We performed coarse-grained modeling of FP_9/10 with SOP force field (Zhmurov et al., 2011). To speed up conformational sampling, we used the under-damped Langevin simulations in the low friction limit. We set ε_h = 0.7 kcal/mol for all residue-residue contacts stabilizing the native state of FP_9/10. Equilibrium contact distances for the intra-monomer contacts were taken from the crystal structure of fibrinogen (PDB structure 3GHG) and for contacts between knobs ‘A’ and holes ‘a’ or selected structures of the D:D interface (PDB structure 1FZG). The contacts formed by knobs ‘A’ were limited to the contacts formed by the active sequence GPR present in the crystal structure of full fibrin(ogen) as a part of GPRP peptide (PDB structure 3GHG). The βN-domains with knobs ‘B’ were incorporated in random coil conformation and were not inserted into holes ‘b’. We performed five 10-ms simulations to explore the conformational transitions in a protofibril FP_9/10, and pilot simulation with the protofibril backbone constrained to explore the span of αC regions and knobs ‘B’.

Structures of αC-region

The αC-connectors were added to the protofibril structure in the extended conformation. The structure of αC-domains (residues Aα392–610) was constructed with Modeller (Webb and Šali, 2017) using sequence homology with the structure of bovine αC-domain (PDB code: 2JOR; Burton et al., 2007). The αC-domain constructs were used as initial structures in all-atom MD simulations. We minimized the energy of αC-domains using the steepest descent algorithm (Brooks et al., 2009), heated αC-domains to 300K, and equilibrated the obtained structures of αC-domains for 1 ms. We randomly selected the structures of αC-domains from the last 500-ns portion of equilibrium simulations and incorporated them into the structure of PF10/9 (38 structures of αC-domain were added to 19 fibrin monomers to construct PF_10/9). Residues Aα392 were connected to the last resolved residue Aα201 in fibrin(ogen) structure 3GHG using random coil conformations of αC-connectors. In coarse-grained modeling, the structures of αC-domains were stabilized by native contacts identified with Modeller; the αC-connectors were assumed to be unstructured.

Calculation of Persistence Length

The persistence length of fibrin protofibril L_p was computed using the output from equilibrium simulations and the worm-like chain formula for the end-to-end distance (R) fluctuations: $R^2=2L_p{L}_0\left[1-\frac{L_p}{L_0}\left(1-exp\left[-\frac{L_0}{L_p}\right]\right)\right]$, where L₀ is the protofibril contour length (Rubinstein and Colby, 2003). We used the first and last D:E:D constructs separated by the contour length of 9 fibrin monomers (L₀ ≈ 9×44.8 nm ≈ 403 nm).

Hydrodynamic Parameters

We used the structures from equilibrium MD simulations of fibrin oligomers and protofibrils. For each oligomer and protofibril, we randomly selected 20 structures to calculate the molar mass M; radius of gyration R_g; translational diffusion coefficient D; protein density ρ; and intrinsic viscosity η (Table 1) using HYDROPRO package (Ortega et al., 2011) and US-SOMO package (Rai et l., 2005). Both packages gave very similar results.

All-Atom MD Simulations

We employed the Solvent Accessible Surface Area (SASA) model of implicit solvation based on CHARMM19 force-field. In the SASA model, the mean solvation energy $\Delta G_{solv}\left(r\right)$ is proportional to the solvent accessible surface area (SASA) of a solute molecule: $\mathrm{\Delta }{G}_{solv}\left(r\right)={\sum }_{i=1}^N{\sigma }_i{A}_i\left(r\right)$, where ${\sigma }_i$ is the atomic solvation parameter and A_i(r) is the SASA for the i-th atom (Ferrara et al., 2002).

Coarse-Graining with Self Organized Polymer (SOP) Model

We employed the native topology-based SOP model of a polypeptide chain (Hyeon et al., 2006), which have been extensively used in the exploration of proteins (Zhmurov et al., 2010a; 2010b; 2011; Alekseenko et al., 2016), to describe the fibrin structure at a residue-based level of detail (energy minimization at Step A in Figure 1C and structural conformations sampling for fibrin protofibril). In this model, each amino acid residue is represented by two interaction centers: for the backbone part (C_α-atom), and for the side-chain (C_β-atom). Hence, a polypeptide chain is replaced by a collection of the C_α- C_α and the C_α-C_β covalent bonds. The positions of the side-chain atoms are selected for each of 20 different amino acids as follows: (i) there is no side-chain for Gly; (ii) for the aliphatic amino acids (Ala, Val, Leu, and Ile), the C_β-bead is placed at the position of the center of mass of the side-chain; (iii) for residues Thr and Ser, the C_β atom is placed at the position of the hydroxyl oxygen; (iv) the side-chain of the acidic amino acids (Asp and Glu) is placed at the center of mass of the COO^- group; (v) the side-chain of the basic amino acids (Lys and Arg) is placed at the center of mass of the NH₃⁺-group; (vi) for Asn and Gln, the C_β-atom is placed at the position of the center of mass of the group CO-NH₂; (vii) aromatic side-chains in Phe and Tyr are represented by the single C_β-bead placed at the geometrical center of the rings (for Tyr, the bead representing the OH-group is also added); (viii) the Trp side-chain having a double-ring structure is represented by two beads placed in the geometrical centers of the rings; (ix) His is represented by a single bead placed at the geometrical center of the five-member ring forming the side-chain; (x) sulfur-containing amino acids (Met, Cys) are represented by the side-chain bead, placed at the position of the sulfur atom; and (xi) the C_γ-atom in Pro is represented by the C_β-bead linked to its C_α-atom and to the C_α-atom of the residue before (thus, forming a cyclic bond structure). The carbohydrate moieties are represented by a set of beads each located at the center of a five-member ring and by peripheral beads for heavy side-chain groups.

SOP Force Field

The potential energy function of the protein conformation U_SOP in terms of the coordinates of C_α- and C_β-atoms {r_i} = r₁, r₂,…, r_N (N is the total number of beads) is given by $U_{SOP}=U_{FENE}+U_{ANG}+U_{NB}^{ATT}+U_{NB}^{REP}$, where specified the first term is the finite extensible nonlinear elastic (FENE) potential $U_{FENE}=-{\sum }_{b=1}^B\frac{k}{2}{R}_0^2\log \left(1-\frac{{\left(r_b-r_b^0\right)}^2}{R_0^2}\right)$ with the spring constant k = 14 N/m and the tolerance for the change of a covalent bond distance R₀ =2 Å. In UFENE, the summation is performed over all the covalently linked beads (C_α- and/or C_β-atoms), B is a total number of covalent bonds in the system, r_b is the distance between the covalently linked atoms, and r_b⁰ is the corresponding equilibrium distance from the energy-minimized full-atomic structure. The following beads are linked covalently: (i) all C_α-atoms along the polypeptide chain forming the backbone; (ii) C_α- and C_β-atoms of the same amino-acid; (iii) C_β-atoms and C_α-atom in the previous residue in Pro; (iv) C_β-atoms in Cys residues forming a mutual disulfide bond; and (v) C_β- atoms in covalently linked residues. Also connected are (vi) the beads in the saccharide unit (C_α- and C_β-atoms), and (vii) the covalently linked saccharides within the same carbohydrate cluster. Additional constraint is imposed on the bond angle formed by a triplet of covalently linked residues by adding the repulsive Lennard-Jones potential for the beads separated by two covalent bonds (1–3 interactions) $U_{ANG}={{\sum }_{a=1}^{N_{ang}}{\epsilon }_{ang}\left({\sigma }_{ang}/r_{ij}\right)}^6$, where ε_ang = 1.0 kcal/mol is the strength of repulsion, and σ_ang = 3.8 Å is the range of repulsion. In UANG, the summation is performed over all N_ang bond angles. To account for the non-covalent (non-bonded) interactions that stabilize the native fold of a biomolecule, we use the harmonic potential $U_{NB}^{ATT}={\sum }_{n=1}^{N_{att}}\frac{k_{nat}}{2}{\left(r_n-r_n^0\right)}^2$ where the summation runs over all N_att pairs of beads that are separated by at least 3 covalent bonds and are within the cutoff distance of r_c =8 Å in the initial (or reference) atomic structure; also, r_n⁰ is the distance between the two interacting beads and rn0 is the corresponding equilibrium distance, taken from the crystal structure (k_nat = 2.0 kcal/mol Å). The rationale for using the harmonic potential in this case is to constrain the amino acids forming a binary native contact in order to preserve the crystal structure. When sampling the conformational space of fibrin protofibril, we use the full Lennard-Jones potential $U_{NB}^{ATT}={\sum }_{n=1}^{N_{att}}{\epsilon }_n\left[{\left(r_n^0/r_n\right)}^{12}-2{\left(r_n^0/r_n\right)}^6\right]$ (Zhmurov et al., 2010a). Here ε_n is the strength of the non-covalent bond, which is usually between 0.6 and 1.3 kcal/mol, depending on the nature of the contact. Using the Lennard-Jones potential allows for the disruption of the native contacts, which is essential while observing the dynamics of the system at equilibrium. The non-native (non-bonded) interactions are treated as repulsive using the Lennard-Jones potential $U_{NB}^{REP}={\sum }_{n=1}^{N_{rep}}{\epsilon }_l{\left({\sigma }_l/r_n\right)}^6$, where the summation runs over all N_rep pairs of beads (C_α- and C_β-atoms) that are neither covalently linked nor form a native contact. We set ε_l = 1 kcal/mol (strength of repulsion) and σ_l = 3.8 Å (range of repulsion).

Structure Alignment

The Kabsch algorithm (Kabsch, 1976) is a method of finding an orthogonal transformation to overlap one set of atomic coordinates (for one structure) with another set of coordinates (for another structure). We take two structures and then select the atoms that are to be aligned. In our implementation, we use the C_α-atoms in globular parts of the molecule. The two sets of coordinates of N atoms are then organized into two 3×N matrices X₁ and X₂. Each row of these matrices corresponds to the Cartesian coordinates of atoms from the first molecule (matrix X₁) and second molecule (matrix X₂). Any two rows in the matrix X₁ and matrix X₂ contain two sets of coordinates of atoms (x₁, y₁, z₁) and (x₂, y₂, z₂) to be aligned. Next, we define the unitary rotation matrix $U={\left(A^{\text{T}}A\right)}^{1/2}{A}^{-1}$ where $A=X_1{}^{\text{T}}{X}_2$ (superscript T denotes the matrix transpose). To overlap the second molecule with the first, we apply the transformation U to the atomic coordinates in the second molecule. Because the Kabsch algorithm minimizes the root-mean-squared deviations (RMSD) for any pair of structures, this method is widely used in the structure alignment of biomolecules. We utilized this approach in the Elongation procedure (see Figure 1B).

Steepest Descent Energy Minimization and Langevin Simulations

To refine the positions of unresolved parts of fibrin molecule added to the crystal structure, we used CHARMM32 force-field for proteins (MacKerell et al., 1998) and CHARMM36 force-field for carbohydrates (Guvench et al., 2011). To introduce the γ-γ crosslinks, we designed a γ-glutamyl-ε-lysyl patch as described in subsection Transglutamination in silico using the atom-type analogy. The system was reconstituted using the CHARMM package (Brooks et al., 2009). The energy minimization was performed using the steepest descent algorithm (Brooks et al., 2009) implemented in our in-house package for GPU-based simulations in implicit solvent (Zhmurov et al., 2012). To preserve the crystal structure, all the resolved parts of the molecules were constrained. We employed the Solvent Accessible Surface Area (SASA) model of implicit solvation (Ferrara et al., 2002), which was re-parameterized to suite CHARMM32/36 force-fields. Next, the energy minimization was performed. We used this approach in the Structure-addition procedure (Figure 1D).

QUANTIFICATION AND STATISTICAL ANALYSIS

Data sample sizes for probability distributions displayed in Figures 4 and 5 are provided in respective figure captions. Average values and standard deviations for data in Figure 4 are presented in Table S2.

DATA AND SOFTWARE AVAILABILITY

Atomic models of fibrin protofibrils are fully available in the form of PDB files for atomic coordinates as Supplementary Data and at http://faculty.uml.edu/vbarsegov/research/fibrin.html.

REAGENT or RESOURCE	SOURCE	IDENTIFIER
Biological Samples
Human fibrinogen	Hyphen BioMed, France	Cat#PP001
Thrombin	Sigma Aldrich, USA	T4393; CAS: 9002–04-4
Deposited Data
Structure of human fibrinogen monomer	Kollman et al., 2009	PDB: 3GHG
Structure of D-dimer from human fibrinogen in bent conformation	Everse et al., 1999	PDB: 1FZG
Structure of D-dimer from human fibrinogen in straight conformation	Yang et al., 2002	PDB: 1N86
Structure of bovine fibrinogen aC-domain	Burton et al., 2007	PDB: 2JOR
Software and Algorithms
VMD	Humphrey et al., 1996	http://www.ks.uiuc.edu/Research/vmd/
CHARMM	Brooks et al., 2009	https://www.charmm.org/
MODELLER	Webb and Sali, 2017	https://salilab.org/modeller/
HYDROPRO	Ortega et al., 2011	http://leonardo.inf.um.es/macromol/programs/hydropro/hydropro.htm
US-SOMO	Rai et al., 2005	http://www.somo.uthscsa.edu/
SOP-GPU	Zhmurov et al., 2010a	http://sop-gpu.readthedocs.io
MDis	Zhmurov et al., 2012	https://github.com/zhmurov/MDis
FemtoScan Online software	Advanced Technologies Center	http://www.femtoscanonline.com
XMGrace	Grace Development Team	http://plasma-gate.weizmann.ac.il/Grace/
Other
Atomic models of fibrin protofibrils	This paper	http://faculty.uml.edu/vbarsegov/research/fibrin.html
Atomic force microscope	Asylum Research - Oxford Instruments, USA	MFP-3D Classic AFM
Cantilevers for atomic force microscopy	Klinov et al., 1998	N/A

Highlights.

• Atomic structures of fibrin oligomers and protofibrils are reconstructed in silico

• Structural models show good agreement with high-resolution AFM images

• Fibrin protofibrils are double-stranded twisted oligomers that can bend and kink

• Hydrodynamic parameters of fibrin oligomers and protofibrils are calculated