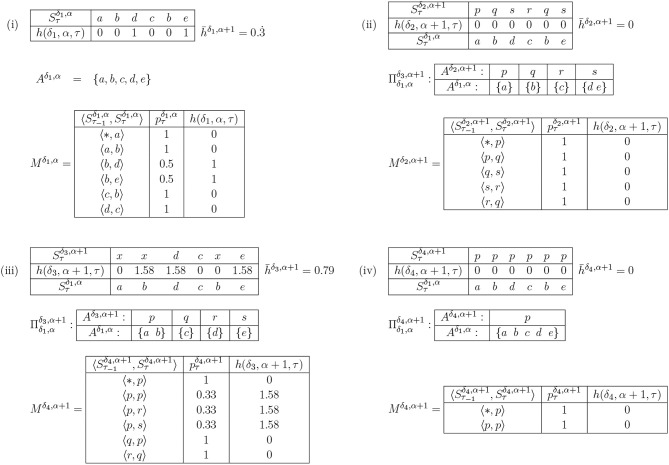
Figure 4.

An example of ${\overline{h}}^{\delta ,\alpha }$ reduction by heuristic selection. (i) shows a very simple example of IDyOT memory (the assumption here is that this is the entire memory). Shown first, in (i), is the memorized sequence along with the information content of each moment. This example is simplified, because the model is derived from the entire string, post-hoc. In a working IDyOT, the statistics would be changing as the string was read. Shown next is the alphabet, A^δ,α. Finally, the bigram model, M^δ,α, is shown (missing pairs of symbols have zero likelihood). It is clear, in this simple case (but also in general), that the uncertainty in the model arises from the choice following a given symbol, here a b; therefore, this is where an attempt should first be made to reduce the alphabet. This is shown in (ii), where ${\Pi }_{{\delta }_1,\alpha }^{{\delta }_2,\alpha +1}$ is a partition of $A^{{\delta }_1,\alpha }$, so that d and e are in the same partition, called p. In this instance, all the uncertainty is removed, and ${\overline{h}}^{\delta ,\alpha }$ for this memory is 0. A new expectation is created for the following symbol, c, which was not available before the categorization, and this is the first glimmer (however small) of creativity caused by re-representation. However, it is possible that this transformation might be vetoed by appeal to the convexity of the resulting region in $V^{{\delta }_2,\alpha +1}$; if so, case (ii) is discarded. Case (iii) shows, for comparison, the effect of categorizing a random pair of symbols, a and b, earlier in the process. Clearly, here, ${\overline{h}}^{\delta ,\alpha }$ increases, and it is easy to see why: the change introduces new uncertainty into M^α+1 which directly affects ${\overline{h}}^{\delta ,\alpha }$ of the memory, and therefore this potential categorization should be rejected. For completeness, case (iv) shows the case where all the symbols are categorized into one partition. This should never arise in practice, under the above procedure, because it is highly unlikely that ${\overline{h}}^{\delta =,\alpha 0}$ would be achievable for a non-trivial example.