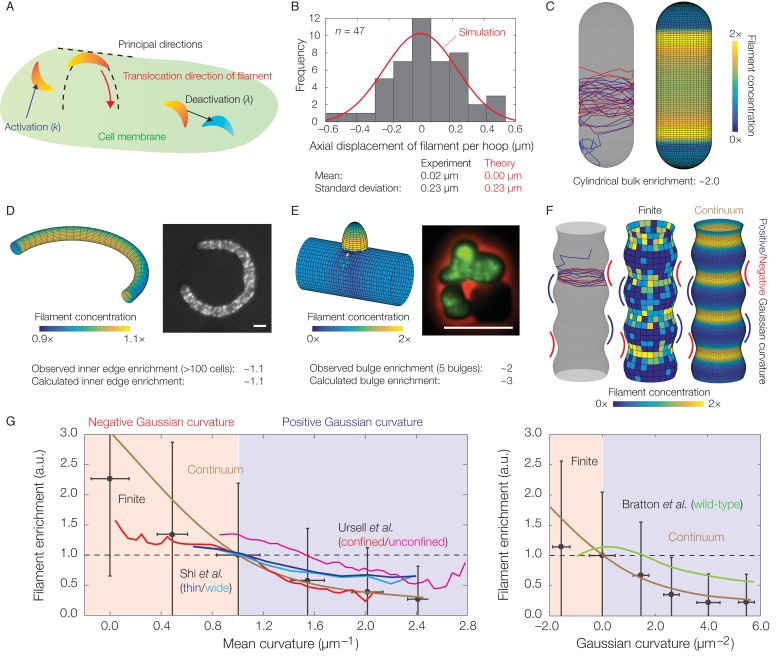
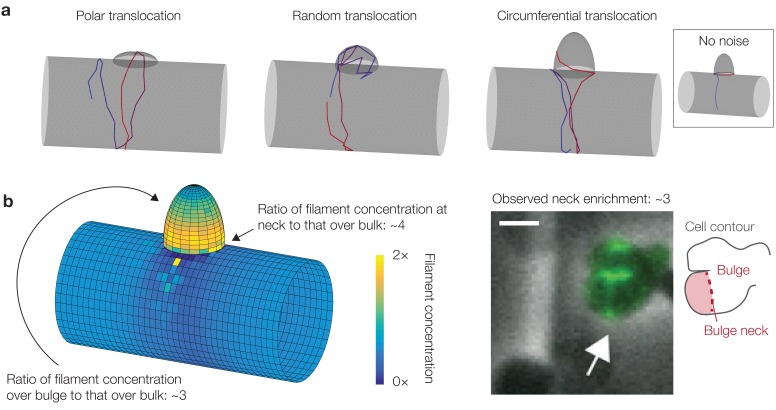
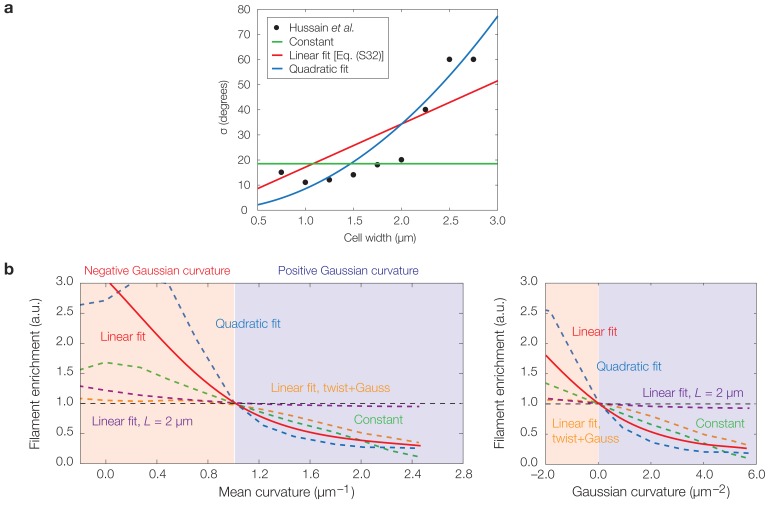
Figure 3. Dynamics of translocation and implications to MreB localization.

In this figure, the localization of MreB filaments, which exhibit a finite processivity and are assumed to follow the parameter values summarized in Supplementary file 2, is shown. (A) A schematic of the model of filament translocation. The filament is modeled as a point which moves processively in a direction determined by the principal curvatures. (B) Histogram of the axial displacements per hoop translocated of 47 MreB filaments in B. subtilis cells (Hussain et al., 2018), along with the theoretical prediction and a simulation result shown. (C) Langevin simulation (left) of Equation (3) and numerical result (right) for the filament concentration, $C_F$, on a spherocylinder, for parameter values relevant to E. coli. Here and below, blue and red denote starts and ends of trajectories, respectively, details of simulations and numerics are provided in Appendix 1, and $C_F$ is found by solving the Fokker-Planck equation corresponding to Equation (3). (D) (Left) Numerical result for $C_F$ on a bent rod, for parameter values relevant to E. coli. (Right) Representative fluorescence microscopy image of an E. coli cell confined to a donut-shaped microchamber, with MreB tagged by green fluorescent protein (GFP), from Wong et al. (2017). The inner edge enrichment is calculated as described in Wong et al. (2017), and the scale bar indicates 1 μm. (E) (Left) Numerical result for $C_F$ on a cylinder with a bulge, for parameter values relevant to B. subtilis. (Right) Representative fluorescence microscopy image of a deformed B. subtilis cell with a bulge and GFP-tagged MreB, from Hussain et al. (2018). The bulge enrichment is calculated as a ratio of average pixel intensities, and the scale bar indicates 5 μm. (F) Langevin simulation and numerical results for $C_F$ on a cylinder with surface undulations in both the finite (Langevin, total of ~500 filaments) and continuum (Fokker-Planck) cases, for parameter values relevant to E. coli. (G) A plot of (left) the mean curvature and (right) the Gaussian curvature against filament enrichment for the figures shown in (F) (Langevin simulation, black; continuum case, brown), with empirically observed relations from confined and unconfined MreB-labeled E. coli cells (red and magenta) from Ursell et al. (2014), thin and wide mutant E. coli cells (blue and cyan) from Shi et al. (2017), and wild-type E. coli cells (green) from Bratton et al. (2018) overlaid. Error bars denote one standard deviation in the Langevin simulation, and 1 a.u. equals the mean of $C_F$ when the mean curvature is 1 µm⁻¹ (left) and when the Gaussian curvature is 0 µm⁻² (right). Note that the magenta and green curves are not normalized according to this convention.

Figure 3—figure supplement 1. Curvature-based translocation on cylinders with bulges.

(a) Three different geometries corresponding to three different translocation behaviors, as summarized in §2.7 of Appendix 1. (b) Same as Figure 3E in the main text. Here $C_F$ is substantially increased at the bulge neck, with a magnitude consistent with previous experiments (Hussain et al., 2018). (Right) Microscopy image of a B. subtilis cell with a bulge and MreB filaments fluorescently tagged, from Hussain et al. (2018). The white arrow highlights the increased fluorescence intensity at a bulge neck, which is indicated by the schematic shown to the right. The scale bar indicates 1 μm.

Figure 3—figure supplement 2. Correlations between Gaussian and mean curvatures for, and translocation directions in, cylinders with undulations of different wavelengths.

(a) Plot of sampled Gaussian curvatures against the corresponding mean curvatures for the geometry considered in §2.8 of Appendix 1 with $a=1$, $c=0.1$, and $P=1$. (b) Same as (a) but for $P=4$. (c) Principal curvatures corresponding to the geometry considered in (b). (d) Dimensionful bending energies of a filament aligning along each principal direction, for the parameter values summarized in Supplementary file 1, showing that, in this geometry as well, binding along the greatest principal direction generally incurs the least bending energy.

Figure 3—figure supplement 3. Effects of curvature-dependent translocation noise and varying filament properties on model predictions.

(a) Plot of experimentally observed median angles from the axis perpendicular to the cellular midline, taken to be identical to σ, against the cell width for B. subtilis cells of varying widths from Hussain et al. (2018). Curves corresponding to the assumptions of a constant σ, a linear fit $\sigma =\alpha {(\mathrm{\Delta }c)}^{-1}$, and a quadratic fit $\sigma =\beta {(\mathrm{\Delta }c)}^{-2}$ are overlaid, where the parameter values α and β are summarized in Supplementary file 2. (b) Same as Figure 3G of the main text, but with continuum limit predictions for the cases of a constant σ (green) and a quadratic fit $\sigma =\beta {(\mathrm{\Delta }c)}^{-2}$ (blue), in addition to the case of a linear fit $\sigma =\alpha {(\mathrm{\Delta }c)}^{-1}$ (red) used in the main text. The continuum limit prediction for the case of a ten-fold larger filament step size, $L=2\mu \text{m}$, is also shown (purple), along with the prediction for the case of large twist and Gaussian curvature-dependent activation (orange; see also Figure 4—figure supplement 4h). Localization therefore arises for the different functional dependencies of σ on $\mathrm{\Delta }c$ shown in (a) and different filament properties.