Variable Selection for Skewed Model-Based Clustering: Application to the Identification of Novel Sleep Phenotypes

Abstract

In sleep research, applying finite mixture models to sleep characteristics captured 8 through multiple data types, including self-reported sleep diary, a wrist monitor capturing movement (actigraphy), and brain waves (polysomnography), may suggest new phenotypes that reflect underlying disease mechanisms. However, a direct mixture model application is challenging because there are many sleep variables from which to choose, and sleep variables are often highly skewed even in homogenous samples. Moreover, previous sleep research findings indicate that some of the most clinically interesting solutions will be those that incorporate all three data types. Thus, we present two novel skewed variable selection algorithms based on the multivariate skew normal (MSN) distribution: one that selects the best set of variables ignoring data type and another that embraces the exploratory nature of clustering and suggests multiple statistically plausible sets of variables that each incorporate all data types. Through a simulation study we empirically compare our approach with other asymmetric and normal dimension reduction strategies for clustering. Finally, we demonstrate our methods using a sample of older adults with and without insomnia. The proposed MSN-based variable selection algorithm appears to be suitable for both MSN and multivariate normal cluster distributions, especially with moderate to large sample sizes.

1. Introduction

1.1. Clinical Motivation

Current psychiatric diagnoses are based almost entirely on self-reported experiences. Unfortunately, treatments for such diagnoses are not effective for all patients. One hypothe-sized reason for this is the “artificial grouping of heterogeneous syndromes with different pathophysiological mechanisms into one disorder” (Cuthbert and Insel, 2013). To address this problem, the National Institute of Mental Health (NIMH) instituted the Research Domain Criteria (RDoC) framework in 2009. RDoC is a research framework that calls for understanding and even potentially refining the boundaries of existing diagnoses by integrating data from multiple levels of information (genes, cells, molecules, circuits, physiology, behavior, and self-report; Insel et al. 2010; Casey et al. 2013; Cuthbert and Insel 2013). Clustering comes to the forefront as a key tool in this effort. Mixture models in particular are useful because they are based on a likelihood, and thus, standard measures such as the BIC can be used to select the optimal number of clusters (Fraley and Raftery, 1998). Applying mixture models to variables captured across multiple levels of information could reveal clusters that are defined by self-report as well as biological processes. Such clusters could help to clarify underlying pathophysiological mechanisms and inform the development of personalized treatments or improved diagnostic classifications.

Sleep medicine is a field for which research within the RDoC framework is particularly valuable (Levenson et al., 2015; Harvey and Tang, 2012; Cuthbert and Insel, 2013). For example, insomnia is characterized by difficulties falling and staying asleep and accompanied by daytime symptoms such as irritability and fatigue (American Psychiatric Association, 2013; Hauri and Sateia, 2005). Clinicians currently only use self-report measures such as a daily sleep diary (Diary) to diagnose individuals with insomnia. However, there is a great deal of heterogeneity in etiology and symptom expression beyond the presence or absence of this diagnosis (e.g., see Vgontzas et al. 2013), and researchers also recognize the importance of objective measures of sleep including actigraphy (ACT; measurement of movement via wrist monitor) and polysomnography (PSG; measurement of electroencephalographic, electromyographic and electrooculographic signals).

As shown in Table 1, Diary, ACT, and PSG each capture some homologous sleep char-acteristics. However, they capture sleep at different levels (self-report, behavioral, physiological), and discrepancies or similarities across homologous measures can be informative (Kay et al., 2015; Lund et al., 2013; Baillet et al., 2016). Also as shown in Table 1, Diary, ACT, and PSG each capture sleep characteristics that are unique to their measurement type. Thus, clustering on Diary, ACT, and PSG measures could indicate how subjective, behavioral, and physiological processes synergistically produce signs and symptoms within homogenous subgroups of individuals.

Table 1:

Diary, actigraphy (ACT), and polysomnography (PSG) characteristics.

Diary, ACT, and PSG (Means and standard deviations (SDs) over 7 nights for Diary and ACT; Means over 2 nights for PSG)

Wake up time (Wake)

Bed time (Bed)

Minutes between bed and wake (Sleep Duration)

Minutes between bed and sleep onset (Sleep Latency, SL)

Minutes awake after first sleep onset (Wake After Sleep Onset, WASO)

Minutes between bed and wake minus WASO and SL (Total Sleep Time, TST)

% minutes asleep after bed time (Sleep Efficiency, SE)

Diary Only (Means and SDs over 7 nights)

Number of awakenings

Sleep quality (Quality)

Mood upon awakening (Mood)

Alertness upon awakening (Alertness)

ACT Only (Means and SDs over 7 nights)

Restlessness based on mobile and immobile periods

Sum of all activity

Average activity per minute

Standard deviation of activity

Maximum activity

PSG Only (Means over 2 nights)

Minutes awake during the 1st half of the night

Minutes awake during the 2nd half of the night

Minutes awake during the last two hours of the night

Minutes of stage N1 sleep (N1)

Minutes of stage N2 sleep (N2)

Minutes of delta (stage N3) sleep (Delta)

Minutes of non-rapid eye movement (i.e., stages N1, N2, and N3) sleep (NREM)

Minutes of rapid-eye movement sleep (REM)

% minutes asleep after sleep onset

% minutes of stage N1 sleep (% N1)

% minutes of stage N2 sleep (% N2)

% minutes of delta (stage N3) sleep (% Delta)

% minutes of NREM sleep (% NREM)

Minutes from sleep onset to REM sleep (REM Latency, RL)

RL minus minutes awake between sleep onset and onset of REM sleep

Stage N3 in 1st NREM period / Stage N3 in 2nd NREM period

The AgeWise sleep study (Buysse et al., 2011) is useful for illustrating the importance of using mixture models to reveal clusters based on Diary, ACT, and PSG measures, as well as the methodological challenges involved. This study followed 216 older adults with (61.1%,N = 132) and without (38.9%,N = 84) insomnia for one week, during which the Pittsburgh Sleep Diary (Monk et al., 1994) and ACT were used to capture sleep characteristics. On two of the seven nights, PSG was also used. We identified 70 Diary, ACT, and PSG characteristics that were clinically meaningful (see Table 1). Although we had no a priori information regarding which specific variables were useful for clustering, we did hypothesize that an explicit subset of variables - including at least one of each of Diary, ACT, and PSG data types - would produce clinically meaningful clusters and inform hypothesis generation.

1.2. Methodological Challenges

The intersection of three methodological challenges preclude the direct application of existing mixture-model-based methods to the AgeWise data. First, clusters are expected to be skewed, requiring the use of a skewed mixture distribution. Second, the consideration of multiple data types produces a large number of correlated variables. This necessitates a method for selecting a subset of useful clustering variables; however, to date, variable selection algorithms based on skewed distributions do not exist. Third, existing variable selection frameworks do not promote the selection of clinically meaningful sets of variables. This latter challenge is particularly salient given our interest in revealing clusters based on self-report, behavioral, and physiological measures of sleep. Further background on each of these three challenges follows.

1.2.1. Challenge 1: Skewed Clusters

In the full AgeWise sample, 79% (55/70) of the variables of interest (Table 1) have significant skewness. In a more homogenous AgeWise subsample such as the 84 older adults without insomnia, the identical set of variables have significant skewness. Many of these variables are counts of minutes awake, and thus, are naturally skewed because they are bounded by zero. For these reasons, we expect that underlying clusters in these sleep data may actually follow a skewed distribution rather than the more commonly assumed normal distribution.

Numerous mixture models based on asymmetric distributions have been developed in recent years. These include approaches based on various forms of the skew normal and skew t distributions (Lin, 2009; Pyne et al., 2009; Lin, 2010; Vrbik and McNicholas, 2012; Cabral et al., 2012; Lee and McLachlan, 2014, 2013b,c; Lachos et al., 2010), including the flexible canonical fundamental skew t-distribution (CFUST; Lee and McLachlan 2016b). There are also mixture models based on the generalized hyperbolic (Browne and McNicholas, 2015; Tortora et al., 2014; Wraith and Forbes, 2015), Poisson (Karlis and Meligkotsidou, 2007), normal inverse Gaussian (Karlis and Santourian, 2009), and Laplace (Franczac et al., 2014) distributions. We are not aware of the use of any of these asymmetric distributions in sleep research.

1.2.2. Challenge 2: A Large Number of Potential Clustering Variables

We identified 70 potentially clinically meaningful Diary, ACT, and PSG variables captured in the AgeWise study (Table 1). However, given the exploratory nature of the research question, there were no a priori hypotheses regarding which variables to include in the clustering model. In the spirit of application, our priority was to maximize the interpretation, utility, and overall clinical relevance of the resulting subgroups. Thus, we aimed to identify an explicit subset of clinically meaningful variables that was useful for clustering.

The challenge of variable selection is compounded by the fact that many of the AgeWise variables are highly correlated or even redundant. The median (Q1, Q3) Spearman correlation magnitude among these variables was 0.11 (0.05,0.22). The maximum correlation was 0.99, observed between N3 and %N3. While these two variables are highly redundant, both have clinical value and it is unknown which one – if either of them – might be useful for clustering.

A well-known stepwise variable selection framework for Gaussian mixture modeling was proposed by Raftery and Dean (2006) with improvements by Maugis et al. (2009). This framework can be implemented with the clustvarsel function (Scrucca and Raftery, 2014) in R (R Core Team, 2015). Other variable selection algorithms include Variable Selection for Classification and Clustering (VSCC), which is based on within-group variance and can be implemented with the vscc function (Andrews and McNicholas, 2013b) in R, and a method by McLachlan et al. (2002) for clustering microarray data. However, because these variable selection algorithms assume normality, we do not hypothesize that they will be appropriate for sleep data. Specifically, we expect that they will tend to select the most highly skewed variables for clustering, regardless of whether these variables are actually useful for revealing underlying skewed subgroups. Because no explicit variable selection algorithm for skewed clusters currently exists, this is an important area of methodological development.

In contrast to the aforementioned approaches that explicitly select a subset of variables for clustering, there are also implicit dimension reduction techniques that suggest clusters based on a weighted combination of all variables. Parsimonious Gaussian Mixture Models (PGMMs) are based on mixtures of factor analyzers (McNicholas and Murphy, 2008, 2010) and are implemented with the pgmm function (McNicholas et al., 2015) in R. There are also implicit dimension reduction approaches based on mixtures of skew normal (Lin et al., 2016), skew t (Murray et al., 2014a,b; Lin et al., 2015), and generalized hyperbolic (Tortora et al., 2016) factor analyzers as well as methods based on the Fisher discriminative subspace (Bouveyron and Brunet, 2012). For non-mixture-model-based clustering, Witten and Tibshirani (2010) developed a dimension-reduction technique called sparse k-means clustering that uses regularization, implemented with the sparcl function (Witten and Tibshirani, 2013) in R. These implicit dimension reduction approaches may be of interest in many applications, but for our aim of revealing clinically meaningful subsets of variables, this feature only makes the clustering results more difficult to interpret.

There have been some comparisons of clustvarsel to other variable selection and dimension reduction methods, including VSCC, PGMM, and sparse k-means clustering (McNicholas and Murphy, 2008; Andrews and McNicholas, 2013a; Witten and Tibshirani, 2010). These comparisons indicated that there may be situations in which clustvarsel is not as effective as other approaches. However, there is no comprehensive evaluation of the accuracy of explicit variable selection algorithms relative to implicit dimension reduction. Thus, it is difficult to determine which strategy might be preferred in any given situation. Further simulation studies must be performed to evaluate explicit variable selection and implicit dimension reduction methods across a range of skewed and normal cluster scenarios.

1.2.3. Challenge 3: Obtaining a Clinically Meaningful Solution

In sleep research, investigators collect Diary, ACT, and PSG measurements because information from all three together provide a deeper understanding of underlying sleep processes. Clusters defined by a set of variables including at least one of each of the three data types are likely to be clinically meaningful, suggest hypotheses to guide researchers in further investigation of underlying disease processes and personalized treatments, and have relevance for the NIMH RDoC framework (Insel et al., 2010). However, given the automated nature of data-driven variable selection algorithms, their application to Diary, ACT, and PSG data will not necessarily suggest a set of variables that contains all three types of variables.

In addition, we expect that there may actually be multiple sets of variables – each including all three data types – that could be used to reveal statistically plausible clustering solutions. Clustering is inherently highly exploratory, and as such, it is reasonable to evaluate multiple solutions and determine which one(s) to pursue depending on the extent to which they provide clinically useful information (Ciu et al., 2007). Thus, it will be important to develop variable selection algorithms that can suggest multiple statistically plausible sets of variables containing Diary, ACT, and PSG data.

1.3. Proposed Solutions

The aforementioned challenges highlight the methodology that needs to be developed and evaluated prior to applying mixture models to Diary, ACT, and PSG data to reveal meaningful clusters. These challenges call for: (1) the development of explicit variable selection algorithms based on asymmetric distributions; (2) further extensions to these algorithms to reveal multiple statistically plausible subsets of variables that each incorporate all data types of interest; and (3) simulations comparing explicit variable selection and implicit dimension reduction techniques.

In light of these needs, we propose two novel variable selection algorithms. The first algorithm, skewvarsel, extends multivariate normal (MVN) algorithms proposed by Raftery and Dean (2006) and Maugis et al. (2009) to the skew normal distribution (Pyne et al., 2009; Azzalini and Valle, 1996). The second algorithm, skewvarsel-p, extends the skewvarsel algorithm by considering all possible permutations of the data types to suggest multiple statistically plausible solutions that each incorporate all data types. This latter algorithm is particularly useful for hypothesis generation in situations where knowledge is expected to be gained by considering multiple data types together (e.g., for research within the NIMH RDoC framework). Through a simulation study, we empirically evaluate and compare the proposed skewvarsel algorithm to other existing explicit variable selection and implicit dimension reduction techniques. Finally, we apply our methods to the AgeWise data (Buysse et al., 2011) to reveal clinically meaningful subgroups based on Diary, ACT, and PSG measures.

2. Methodology

2.1. Multivariate Skew Normal Distribution

The proposed skewed variable selection algorithms can in principle be used with any asymmetric distribution. We initiate our work using the multivariate skew normal (MSN) distribution proposed by Pyne et al. (2009) and Azzalini and Valle (1996), sometimes also called the “restricted” MSN distribution (Lee and McLachlan, 2013c). Although this MSN distribution is known to be less flexible than other asymmetric distributions (Lee and McLachlan, 2013c), it is easily embedded within our proposed variable selection algorithm because it is computationally efficient, does not overly rely on starting values, converges relatively quickly, and has both regression and mixture model estimation tools available. Furthermore, we hypothesize that potential limitations related to use of the MSN distribution for variable selection can be overcome by fitting a more flexible asymmetric mixture model (e.g., the CFUST, Lee and McLachlan 2016b) to the selected variables.

For p ≥ 1 dimensions, the MSN density as presented by Pyne et al. (2009) is

$$f(\mathbf{y};\mathit{\mu },\mathbf{\Sigma },\mathit{\delta })=2{\varphi }_p(\mathbf{y};\mathit{\mu },\mathbf{\Sigma }){\mathrm{\Phi }}_1\left({\mathit{\delta }}^T{\mathbf{\Sigma }}^{-1}(\mathbf{y}-\mathit{\mu });\mathbf{0},\mathbf{1}-{\mathit{\delta }}^T{\mathbf{\Sigma }}^{-1}\mathit{\delta }\right),$$ (1)

where ϕ_p and Φ_p are the standard p-dimensional MVN pdf and cdf, respectively; Σ is the scale matrix; δ is the vector of parameters indicating the skewness of each dimension; and μ is the location parameter vector. Likelihood inference for the MSN distribution is discussed by Azzalini and Genton (2008). In univariate regression models, the location parameter of the i^th individual, μ_i, is modeled as x_iβ, where x_i is a 1 × p dimensional set of covariate values and β is a p × 1-dimensional vector of regression parameters. We use the selm function in the sn package (Azzalini, 2014) in R to fit regression models.

The mixture model based on the MSN distribution is

$$f(\mathbf{y};\mathbf{\Theta })={\displaystyle \sum _{g=1}^G}{\pi }_{g}f\left(\mathbf{y};{\mathbf{\Theta }}_g\right),$$

where f(y;Θ_g) is the MSN density for cluster g as given in equation (1), ${\displaystyle {\sum }_{g=1}^G{\pi }_g=1}$, Θ_g = {μ_g,Σ_g,δ_g}, and Θ = {Θ₁,Θ₂,...,Θ_G} is the set of all unknown parameters across the G clusters. Parameters can be estimated using the EM algorithms presented by Pyne et al. (2009) and Cabral et al. (2012), implemented through the EMMIXSkew package (Wang et al., 2013) in R. In this package, the within-cluster covariance can take one of 5 different patterns.

2.2. Bayes Factors for Comparing Skewed Clustering Models

A landmark method for variable selection in model-based clustering was presented by Raftery and Dean (2006). At each step of their variable selection algorithm, they partition the data as Y = {Y_C,Y_j,Y_NC}, where Y_C represents the subset currently used for clustering, Y_j represents the variable currently being considered for inclusion, and Y_NC represents the remaining “non-clustering” variables. They use a Bayes factor (Kass and Raftery, 1995) to assess whether the evidence for clustering on both Y_C and Y_j outweighs the evidence for clustering only Y_C alone. Their method accounts for the association between Y_j and Y_C through a regression of Y_j on Y_C.

A criticism of the strategy proposed by Raftery and Dean (2006) is that it over-penalizes potential clustering variables Y_j that are not related to all components of Y_C. Thus, Maugis et al. (2009) extended the method by allowing for Y_j to depend on only a (possibly null) subset of Y_C, denoted Y_R(j), selected through backwards stepwise regression. In turn, Scrucca and Raftery (2014) extended the method to use best subset regression to select Y_R(j), implemented with the clustvarsel function in R.

Motivated by Raftery and Dean (2006) and Maugis et al. (2009), our variable selection algorithm is driven by the iterative comparison of two models,

$$M_1:f\left(Y_C,Y_j,Y_{NC}|C,M_1\right)=f\left(Y_{NC}|Y_j,Y_C\right)f\left(Y_j|Y_{R(j)},M_1\right)f\left(Y_C|C,M_1\right)$$

versus

$$M_2:f\left(Y_C,Y_j,Y_{NC}|C,M_2\right)=f\left(Y_{NC}|Y_j,Y_C\right)f\left(Y_j,Y_C|C,M_2\right).$$

In this model comparison, f(Y_j|Y_R(j),M₁) is the likelihood from a MSN regression of Y_j on Y_R(j), and f(Y_C|M₁) and f(Y_C,Y_j|M₂) are the likelihoods from MSN mixture models of Y_C and {Y_C,Y_j}, respectively. In model M₁, a variable Y_j considered for clustering provides no additional information about cluster membership C after conditioning on Y_R(j) ⊆ Y_C. In model M₂, Y_j provides information about cluster membership C above and beyond Y_C.

As proposed by Raftery and Dean (2006) and further discussed by Maugis et al. (2009), models M₁ and M₂ can be compared using a Bayes factor,

$$B_{12}=\frac{f(Y|M_1)}{f(Y|M_2)}=\frac{f\left(Y_j|Y_{R(j)},M_1\right)f\left(Y_C|M_1\right)}{f\left(Y_j,Y_C|M_2\right)}.$$

Because Bayes factors are difficult to compute, a useful approximation by Kass and Raftery (1995) is

$$2\log B_{12}\approx BIC\left(M_1\right)-BIC\left(M_2\right),$$ (2)

where BIC = 2 log (maximized likelihood) − p log(n), p is the number of independent parameters in the model, and n is the sample size.

We express BIC(M₁) in equation (2) as

$$BI{C}_1\left(Y_j|Y_C\right)=BI{C}_R\left(Y_j|Y_{R(j)}\right)+\underset{2\le g\le G,m\in M}{\max }BI{C}_{C(g,m)}\left(Y_C\right),$$ (3)

where BIC_R(Y_j|Y_R(j)) is the BIC from the MSN regression of Y_j on Y_R(j), BIC_C(g,m)(Y_C) is the BIC from the MSN mixture model of Y_C with g subgroups and covariance pattern m, and M is the set of covariance patterns considered. Similarly, we express BIC(M₂) in equation (2) by

$$BI{C}_2\left(Y_j|Y_C\right)=\underset{2\le g\le G,m\in M}{\max }BI{C}_{C(g,m)}\left(Y_j,Y_C\right),$$ (4)

where BIC_C(g,m)(Y_j,Y_C) is the BIC from the MSN mixture model of {Y_C,Y_j} with g sub-groups and covariance pattern m. Thus, the approximation to 2logB₁₂ in equation (2) can be written as

$$\mathrm{\Delta }BIC\left(Y_j|Y_C\right)=BI{C}_1\left(Y_j|Y_C\right)-BI{C}_2\left(Y_j|Y_C\right),$$ (5)

where BIC₁(Y_j|Y_C) and BIC₂(Y_j|Y_C) are given in equations (3) and (4), respectively. When ΔBIC(Y_j|Y_C) is sufficiently negative, Y_j provides additional information about the cluster membership after considering variables Y_C already in the model. When ΔBIC(Y_j|Y_C) is sufficiently positive, Y_j does not provide additional information about cluster membership after considering variables Y_C already in the model. Finally, when Y_C is null (i.e., no variables are already entered in the clustering model), we evaluate the evidence of univariate clustering on a variable Y_j as

$$\mathrm{\Delta }BIC\left(Y_j\right)=BI{C}_R\left(Y_j\right)-\underset{2\le g\le G,m\in M}{\max }BI{C}_{C(g,m)}\left(Y_j\right),$$ (6)

where BIC_R(Y_j) is the BIC from an intercept-only regression of Y_j and BIC_C(g,m)(Y_j) is the BIC from a univariate skew normal mixture model of Y_j with g clusters and covariance structure m.

2.3. Skewed Variable Selection Algorithm

In this section we present our proposed skewvarsel algorithm, within which the MSN mixture model comparisons detailed in section 2.2 are embedded. The algorithm is similar to the one presented by Raftery and Dean (2006). However, like Maugis et al. (2009), we allow only a subset of variables Y_R(j) ⊆ Y_C to be related to Y_j, with Y_R(j) selected through a stepwise regression algorithm. We assume a relatively large pool of initial variables (e.g., 70 in the AgeWise data); thus, we use forward selection to create Y_R(j) because it requires fitting fewer and lower-dimensional models.

The main steps of the skewvarsel algorithm are: (1) considering all possible variables, select the single variable most useful for clustering; (2) considering all possible remaining variables, select the second variable most useful for bivariate clustering along with the first variable; and (3) iteratively enter and remove variables to improve model fit until the set stabilizes. In detail, Y represents the full set of variables, Y\Y₁ denotes all of Y except Y₁, and δ_I and δ_R are the BIC difference thresholds that indicate enough evidence to include or remove a variable, respectively.

• Step 1: Inclusion. Calculate ΔBIC(Y_j) in (6) for each Y_j ∈ Y. Select $Y_{j_1}$ such that j₁ = argmin_j ΔBIC(Y_j). Create Y_C = $Y_{j_1}$ and Y_NC = Y \Y_C.

• Step 2: Inclusion. Calculate ΔBIC(Y_j|Y_C) in (5) for each Y_j ∈ Y_NC. Select $Y_{j_2}$ such that j₂ = argmin_j ΔBIC(Y_j|Y_C). Update Y_C = Y_C ∪ $Y_{j_2}$ and Y_NC = Y \Y_C.

• Step 3. Iteration. Iterate between inclusion and removal steps until no variables are entered or removed or the same variable is entered and removed.

  • –
    Inclusion. Calculate ΔBIC(Y_j|Y_C) for each Y_j ∈ Y_NC. Select $Y_{j_i}$ for inclusion such that j_i = argmin_j ΔBIC(Y_j|Y_C) only if min_j ΔBIC(Y_j|Y_C) ≤ δ_I. If a variable is selected for inclusion, update Y_C = Y_C ∪ $Y_{j_i}$ and Y_NC = Y \Y_C.
  • –
    Removal. Calculate ΔBIC(Y_j|Y_C\Y_j) for each Y_j ∈ Y_C. Select $Y_{j_{i+1}}$ for removal such that j_i+1 = argmax_j ΔBIC(Y_j|Y_C\Y_j) only if max_j ΔBIC(Y_j|Y_C\Y_j) ≥ δ_R. If a variable is selected for removal, update Y_NC = Y_NC ∪ $Y_{j_{i+1}}$ and Y_C = Y \Y_NC.

Embedded within the skewvarsel algorithm is the computation of BIC_R(Y_j|Y_R(j)) in equation (3), the BIC from the MSN regression of Y_j on Y_R(j), where Y_R(j) ⊆ Y_C is selected through a forward selection algorithm. The main steps of this forward selection algorithm are: (1) select the single variable in Y_C most useful for predicting Y_j (if no variable is useful, stop); (2) determine the second variable in Y_C most useful for predicting Y_j along with the first variable (if no additional variable is useful stop); (3) iteratively enter and remove variables in Y_C for predicting Y_j until the algorithm stabilizes. In detail, ΔBIC_R(Y_j|Y₁) = BIC_R(Y_j)−BIC_R(Y_j|Y₁) is the BIC difference between MSN regressions of Y_j alone and Y_j on Y₁. Similarly, ΔBIC_R(Y_j|Y₁,Y₂) = BIC_R(Y_j|Y₁) − BIC_R(Y_j|Y₁,Y₂) is the BIC difference between MSN regressions of Y_j on Y₁ and Y_j on {Y₁,Y₂}. To simplify notation, we again use δ_I and δ_R to denote the BIC difference thresholds required to enter or remove a variable. However, in practice, the thresholds used for the clustering and regression variable selection algorithms can differ.

• Step 1. Calculate ΔBIC_R(Y_j|Y_l) for each Y_l ∈ Y_C. Select $Y_{l_1}$ such that l₁ = argmin_l ΔBIC_R(Y_j|Y_l) only if min_l ΔBIC_R(Y_j|Y_l) ≤ δ_I. If a variable is selected set Y_R(j) = $Y_{l_1}$ and continue to step 2. Otherwise stop.

• Step 2. Calculate ΔBIC_R(Y_j|Y_R(j),Y_l) for each Y_l ∈ Y_C\Y_R(j). Select $Y_{l_2}$ such that l₂ = argmin_l ΔBIC_R(Y_j|Y_R(j),Y_l) only if min_l ΔBIC_R(Y_j|Y_R(j),Y_l) ≤ δ_I. If a variable is selected update Y_R(j) = Y_R(j) ∪ $Y_{l_1}$ and continue to step 3. Otherwise stop.

• Step 3. Iteration. Iterate between inclusion and removal steps until no variables are entered or removed or the same variable is entered and removed.

  • –
    Inclusion. Calculate ΔBIC_R(Y_j|Y_R(j),Y_l) for each Y_l ∈ Y_C\Y_R(j). Select $Y_{l_i}$ for inclusion such that l_i = argmin_l ΔBIC_R(Y_j|Y_R(j),Y_l) only if min_l ΔBIC_R(Y_j|Y_R(j),Y_l) ≤ δ_I. If a variable is selected for inclusion update YR(j) = YR(j) ∪$Y_{l_i}$.
  • –
    Removal. Calculate ΔBIC_R(Y_j|Y_R(j)\Y_l,Y_l) for each Y_l ∈ Y_R(j). Select $Y_{l_{i+1}}$ for removal such that l_i+1 = argmax_l ΔBIC_R(Y_j|Y_R(j)\Y_l,Y_l) only if max_l ΔBIC_R(Y_j|Y_R(j)\Y_l,Y_l) ≥ δ_R. If a variable is selected for removal set Y_R(j) = Y_R(j)\$Y_{l_{i+1}}$.

A notable difference between the regression and clustering variable selection algorithms is that in the regression algorithm we require the BIC difference to meet the threshold δ_I at the very first step in order to continue, whereas in the clustering algorithm we only require the BIC difference to meet the threshold δ_I in the iterative steps. This is because we want to promote selection of at least one variable in the clustering variable selection algorithm, but prefer efficiency in the regression variable selection algorithm embedded within it. These criteria can be altered depending on the specific research aims and data.

2.4. Skewed Variable Selection Algorithm Considering Data Type

In a data set with many potential clustering variables, we expect that there are many statistically plausible sets of variables for clustering, some which produce more clinically meaningful solutions than others. Thus, in the spirit of exploratory data analysis, we propose a variable selection algorithm called skewvarsel-p. It is based on the skewvarsel algorithm but uses permutations of data types to suggest multiple statistically plausible sets of variables that each incorporate at least one of every data type. The use of permutations in this way allows for exploration of multiple solutions, thereby maximizing one’s ability to reveal at least one solution that is clinically meaningful. This algorithm is relevant for research within the NIMH RDoC framework as well for any investigator interested in revealing solutions that incorporate one of each data type.

For each permutation of data types, the main steps of the algorithm are: (1) sequentially enter the variable of each data type that is most useful for clustering, thereby establishing a pool of variables containing at least one of every data type; (2) enter an additional variable of any data type; and (3) iteratively enter and remove variables until the algorithm stabilizes. In the iterative step 3, we do not allow for the first set of variables (selected in step 1) to be removed in order to ensure one of each data type is included. However, if one does not want to force one of each data type, this criterion can be relaxed. In detail, we consider K data types denoted D₁,...,D_K. There are π = 1,...,K! ways to permute these data types. We denote D_π(1),...,D_π(K) as the ordered data types from the π^th permutation, such that data type D_π(k) produces the set of variables Y_π(k). Because the selection of a variable depends on the variables selected before it, our strategy is to apply a variable selection algorithm to each of the K! permutations of data types. The algorithm for the π^th permutation follows, and uses the same stepwise algorithm for selecting Y_R(j) as detailed in the skewvarsel algorithm in section 2.3.

• Step 1. Inclusion of data type D_π(1): Calculate ΔBIC(Y_j) in (6) for each Y_j ∈ Y_π(1). Select $Y_{j_1}$ such that j₁ = argmin_j ΔBIC(Y_j). Set $Y_{C_1}=Y_{j_1}$ and Y_NC = Y \$Y_{C_1}$.

• Steps k = 2,...,K. Inclusion of data type D_π(k): Calculate ΔBIC(Y_j|$Y_{C_1}$) in (5) for each Y_j ∈ Y_π(k). Select $Y_{j_k}$ such that j_k = argmin_j ΔBIC(Y_j|$Y_{C_1}$). Update $Y_{C_1}=Y_{C_1}\cup Y_{j_k}$ and YNC = Y \$Y_{C_1}$.

• Step K +1. Inclusion of any data type: Calculate ΔBIC(Y_j|$Y_{C_1}$) for each Y_j ∈ Y_NC. Select the (K+1)^st clustering variable $Y_{j_{K+1}}$ such that j_K+1 = argmin_j ΔBIC(Y_j|$Y_{C_1}$) only if min_j ΔBIC(Y_j|$Y_{C_1}$) ≤ δ_I. If a variable is selected set $Y_{C_2}=Y_{j_{K+1}}$, Y_C = {$Y_{C_1}$,$Y_{C_2}$}, Y_NC = Y \Y_C, and proceed to the iterative step. Otherwise stop.

• Step K +2. Iteration: Iterate between inclusion and removal steps until no variables are entered or removed or the same variable is entered and removed.

  • –
    Inclusion: Calculate ΔBIC(Y_j|Y_C) for each Y_j ∈ Y_NC. Select $Y_{j_i}$ for inclusion such that j_i = argmin_j ΔBIC(Y_j|Y_C) only if argmin_j ΔBIC(Y_j|Y_C) ≤ δ_I. If a variable is selected for inclusion set $Y_{C_2}=Y_{C_2}\cup Y_{j_i},Y_C=\left\{Y_{C_1},Y_{C_2}\right\}$, and Y_NC = Y \Y_C.
  • –
    Removal: Calculate ΔBIC(Y_j|Y_C\Y_j) for each Y_j ∈$Y_{C_2}$. Select $Y_{j_{i+1}}$ for removal such that j_i+1 = argmax_j ΔBIC(Y_j|Y_C\Y_j) only if argmax_j ΔBIC(Y_j|Y_C\Y_j) ≥ δ_R. If a variable is selected for removal, update $Y_{C_2}=Y_{C_2}\backslash Y_{j_{i+1}},Y_C=\left\{Y_{C_1},Y_{C_2}\right\}$, and YNC = Y\YC.

Our focus is on an application with only three data types; thus, searching for sets of clustering variables based on all six permutations is reasonable. However, it is inevitable that one would eventually consider more than three data types. Just four data types produces 24 sets of variables, which may already be too overwhelming and time consuming to sort through. Two adaptations to streamline the above strategy are: (1) only consider permutations beginning with the variable(s) that have the strongest evidence of univariate clustering; and (2) instead of considering all permutations, enter the first variable with the strongest evidence of univariate clustering based on any data type, enter the second variable with the strongest evidence of bivariate clustering among the remaining data types, and so on. This latter strategy produces a single set of clustering variables that incorporates all data types. Finally, although the skewvarsel-p algorithm was motivated by our desire to select subsets containing one variable of each data type, it can be easily generalized to select subsets containing one variable from each of any pre-specified groupings. For example, after performing a factor analysis, one could apply this algorithm to select one variable that loaded on each identified factor.

2.5. Data Generation

We evaluated the proposed skewvarsel algorithm relative to other explicit and implicit dimension reduction techniques when variables are skewed, considering both MSN and MVN cluster scenarios. For each scenario, we generated two variables {X₁,X₂} that are informative for dividing the sample into three clusters based on a clustering assignment C, two variables {X₃,X₄} that are unrelated to C, and two variables {X₅,X₆} that are related to X₁ and X₂, respectively, but which do not actually provide any information about C after conditioning on X₁ and X₂.

Parameter values for X₁ and X₂ (clustering variables) within MSN and MVN cluster scenarios were selected by fitting MSN and MVN mixture models to PSG %N3 and PSG Bed variables from the AgeWise data. These variables were selected because both MSN and MVN mixture models suggested three clusters based on these two variables, and because %N3 is significantly skewed and Bed is not.

For the MSN scenario, parameter values for X₃ and X₄ (irrelevant variable)s were selected by fitting MSN distributions to Diary Quality and PSG SL variables. Neither was shown to be useful for univariate MSN clustering, but SL was highly skewed and Quality was not. For the MVN scenario, parameter values for X₃ and X₄ were selected by fitting MVN distributions to Diary Quality and Diary Mood variables; neither was shown to be useful for univariate MVN clustering and neither was significantly skewed. For both MSN and MVN scenarios, X₅ and X₆ (correlated variables) were generated by adding noise to X₁ and X₂, respectively. Further details on parameter values and data generation are provided in Table 2.

Table 2:

Parameters for MVN and MSN cluster scenarios in the simulation study.

Multivariate Normal: MVN (μ, σ)	Multivariate Skew Normal: MSN (μ,σ,δ)
Clustering Variables
[Xlg,X2g] ~ MVN(μg, Σg)	[X1g,X2g] ~ MSN(μg,Σg,δg)
μ1 = [0.50, 4.00], ${\mathbf{\Sigma }}_1=\left[\begin{array}{ll}3.00\hfill & 0.02\hfill \\ 0.02\hfill & 0.90\hfill \end{array}\right]$	μ1 = [-0.20,18.00], ${\mathbf{\Sigma }}_1=\left[\begin{array}{cc}0.011& -0.013\\ -0.013& 1.42\end{array}\right]$, δ1 = [2.60, 3.90]
μ2 = [14.00, 21.00], ${\mathbf{\Sigma }}_2=\left[\begin{array}{cc}3.00& -0.10\\ -0.10& 1.00\end{array}\right]$	μ2 = [9.00, 23.00], ${\mathbf{\Sigma }}_2=\left[\begin{array}{cc}53.50& -0.99\\ -0.99& 0.17\end{array}\right]$, δ2 = [1.40, -0.30]
μ3 = [23.00, 23.50], ${\mathbf{\Sigma }}_3=\left[\begin{array}{cc}55.10& 1.80\\ 1.80& 0.90\end{array}\right]$	μ3 = [26.00, 24.50], ${\mathbf{\Sigma }}_3=\left[\begin{array}{cc}21.20& -0.24\\ -0.24& 0.13\end{array}\right]$, δ3 = [-0.90, -1.10]
p1 = 0.40, p2 = 0.30, p3 = 0.20	p1 = 0.54, p2 = 0.14, p3 = 0.32
Irrelevant Variables
X3 - MVN(68.00, 287.00)	X3 ~ MSN(0.40, 2.00, 31.00)
X4 - MVN(60.00, 296.00)	X4 ~ MSN(62.00, 292.00,0.00)
Correlated Variables
X5 = X1 + Z1, Z1 ~ MVN(0,60)	X5 = X1 + Z1, Z1 ~ MSN(0.00,60.00,3.00)
X6 = X2 + Z2, Z2 ~ MVN(0,3)	X6 = X1 + Z1, Z1 ~ MSN(0.00,3.00,0.00)

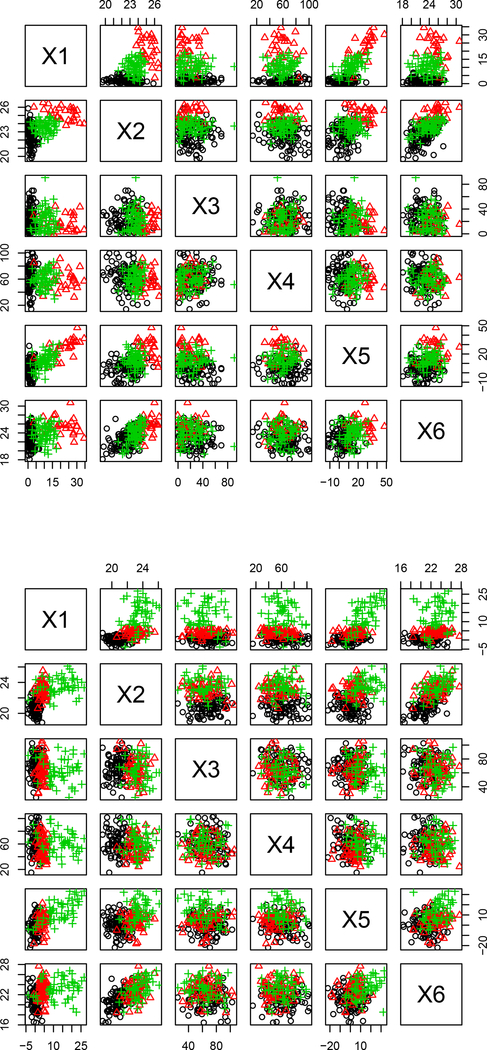
We generated 1000 data sets for each of three sample sizes (N = 200, N = 500, and N = 800) for both MSN and MVN scenarios. In the MSN scenario with N = 500, the mean(SD) Spearman correlations of interest were 0.48(0.03) for {X₁,X₂}, 0.70(0.02) for {X₁,X₅}, and 0.61(0.03) for {X₂,X₆}. In the MVN scenario with N = 500, the mean (SD) Spearman correlations of interest were 0.54(0.03) for {X₁,X₂}, 0.64(0.03) for {X₁,X₅}, and 0.65(0.03) for {X₂,X₆}. Considering these moderately large correlations, we expect that our simulation scenarios represent moderate-to-difficult clustering problems. Example data are shown in Figure 1.

Figure 1:

Sample simulated data sets with MSN (top) and MVN (bottom) clusters.

2.6. Model Fitting and Summary

For each of the 1000 simulated data sets in each of six scenarios (MSN and MVN clusters; N = 200, 500, and 800) we applied three explicit variable selection algorithms: (1) skewvarsel, (2) clustvarsel (Scrucca and Raftery, 2014), and (3) vscc (Andrews and McNicholas, 2013b). For skewvarsel and clustvarsel variable selection, we set δ_I = δ_R = 0 and considered 1 − 6 clusters and all available covariance patterns. The vscc algorithm assumes > 1 cluster exists; thus only 2−6 clusters were considered. After explicit variable selection, we computed the percentages of correct variable sets, number of times each specific variable was selected, and number of times no variables were selected.

For each of 500 simulated data sets, we used each identified subset of variables (selected through skewvarsel, clustvarsel, or vscc) to fit mixture models based on three distributions: (1) MVN, (2) MSN, and (3) CFUST (clustvarsel and skewvarsel only; N = 200 only). Both MVN and MSN mixture models were fit to ensure that distributional problems related to variable selection versus the subsequent fitting of the mixture model were not conflated. CFUST mixture models were fit because they are are highly flexible asymmetric distributions (Lee and McLachlan, 2016b) and we hypothesized that they could improve model accuracy. However, CFUST models were only fit in the N = 200 scenario to variables selected through clustvarsel and skewvarsel. This is because they can be extremely computationally intensive, often requiring > 24 hours to obtain a single final model result with larger N (e.g., N = 500 or N = 800) and/or with > 2 variables (as tended to be selected through vscc).

We also applied two implicit dimension reduction approaches to all six simulated variables: (1) parsimonious Gaussian mixture models (PGMM; McNicholas and Murphy 2008); and (2) sparse k-means clustering (Witten and Tibshirani, 2010). We fit sparse k-means models to all 1000 simulated data sets. We fit PGMM to only 500 simulated data sets because it is a much more computationally intensive model.

For all mixture-model-based clustering approaches (CFUST, MSN, and MVN mixture models fit to selected subsets of variables; PGMM), we allowed for any available covariance pattern, considered 1 − 6 clusters, and 1 − 2 factors where relevant. For sparse k-means clustering, we rescaled each variable to the range [0,1] with the transformation (X − X_min)/(X_max − X_min) and used the sparcl function in R (Witten and Tibshirani, 2013). We used 200 permutations to select the best tuning parameter for each cluster number and applied the gap statistic with 500 bootstrap samples to select among 1 − 6 clusters. Additional computational details (e.g., initialization, likelihood tolerance, R functions) for all models are provided in Table 3.

Table 3:

Computing details for fitting clustering models. For all mixture models, the EM likelihood tolerance was set to 1e−5.

Model	R Function	R Package (Citation)	Initializations	Maximum Iterations
MVN Mixture Model	Mclust	mclust (Fraley et al., 2012)	hierarchical	1000
MSN Mixture Model	EmSkew	EMMIXskew (Wang et al., 2013)	20 k-means	1000
CFUST Mixture Model	fmcfust	EMMIXcskew (Lee and McLachlan, 2016a)	MSN, MST1	1000
PGMM	pgmmEM	pgmm (McNicholas et al., 2015)	hierarchical, random, k-means	NA2
Sparse k-means Clustering	sparcl	sparcl (Witten and Tibshirani, 2013)	NA3	NA3

Finally, for each selected clustering model, we recorded the number of clusters and calculated the Adjusted Rand Index (ARI, Hubert and Arabie 1984) if more than one cluster was identified. The ARI quantifies the level of cluster recovery, that is, the similarity between the true and estimated cluster assignments. An ARI of one (the maximum value) indicates perfect cluster recovery. ARI cutoff values of 0.9, 0.8, and 0.65 indicate excellent, good, and moderate recovery, respectively. ARI values < 0.65 suggest poor recovery. The expected value of the ARI under random classification is zero (Steinley, 2004). R was used for all data generation, model-fitting, and summary methods within the simulation.

2.7. Explicit Variable Selection Results (Table 4)

Table 4:

Variable selection results from 1000 data sets in each scenario. X₁ and X₂ are useful for clustering, X₃ and X₄ are independent of X₁ and X₂ and are not useful for clustering, and X₅ and X₆ are not useful for clustering after conditioning on X₁ and X₂.

Selection Algorithm	N	% Correct	%X1	%X2	%X3	%X4	%X5	%X6	% None
MSN Clusters
vscc	200	3.3	100.0	95.6	62.1	59.8	95.8	69.4	0.0
	500	0.0	100.0	94.9	72.4	67.9	99.7	69.2	0.0
	800	0.1	100.0	89.5	76.5	67.0	99.8	67.4	0.0
clustvarsel	200	15.6	100.0	16.8	48.3	0.0	0.1	0.7	0.0
	500	13.5	100.0	28.7	85.8	0.0	0.0	0.0	0.0
	800	5.3	100.0	52.3	94.7	0.0	0.0	0.0	0.0
skewvarsel	200	43.2	99.3	47.9	0.0	0.6	12.7	7.4	0.7
	500	65.1	100.0	69.0	0.0	0.4	9.4	2.5	0.0
	800	84.2	100.0	89.4	0.0	0.5	6.2	1.2	0.0
MVN Clusters
vscc	200	2.3	100.0	98.4	67.6	67.6	94.1	91.0	0.0
	500	0.1	100.0	93.4	78.6	78.6	98.6	90.2	0.0
	800	0.0	100.0	79.3	50.1	50.4	96.4	76.2	0.0
clustvarsel	200	74.0	100.0	76.4	0.5	0.3	1.5	2.3	0.0
	500	99.6	100.0	99.9	0.1	0.0	0.2	0.0	0.0
	800	99.8	100.0	100.0	0.1	0.0	0.1	0.0	0.0
skewvarsel	200	90.0	100.0	98.5	1.0	1.6	4.9	2.4	0.0
	500	98.0	100.0	100.0	0.6	0.3	1.1	0.0	0.0
	800	99.9	100.0	100.0	0.0	0.1	0.0	0.0	0.0

2.7.1. MSN Clusters

When clustering variables were mixtures of MSN clusters, the MVN-based clustvarsel algorithm identified the correct subset of variables in only 5 − 16% of the simulations. It tended to ignore X₂ (useful for MSN clustering, not skewed), in favor of X₃ (not useful for MSN clustering, skewed). Its performance declined with larger sample sizes, most likely because the larger N provided more power to reveal MVN clusters within the skewedyet-irrelevant X₃ variable. The MSN-based skewvarsel identified the correct subset of variables for 43 − 84% of the simulations and improved with larger sample sizes. It had difficulty identifying X₂ but rarely selected other irrelevant or correlated variables. The vscc algorithm selected the correct subset in only 3% of the simulations. It almost always selected the correct clustering variables (X₁ and X₂) but along with these also selected the other non-clustering variables, especially the correlated variables. Thus, for variable selection with underlying MSN clusters, skewvarsel out-performed clustvarsel and vscc.

2.7.2. MVN Clusters

When clustering variables were mixtures of MVN clusters, both skewvarsel and clustvarsel variable selection algorithms identified the correct variables the majority of the time. With N = 200, skewvarsel performed even better than clustvarsel, identifying the correct subset of variables in 90% of the simulations (compared to 74% from clustvarsel). The performance of the vscc algorithm in the MVN cluster scenario was similar to its performance in the MSN cluster scenario. It selected the correct subset of variables in only 2% of the data sets and tended to select a larger subset than necessary. Thus, for vari-able selection skewed variables and MVN clusters, both skewvarsel and clustvarsel out-performed vscc.

2.8. Clustering Results

2.8.1. MSN Clusters (Table 5; Figure 2)

Table 5:

Results from the MSN cluster scenario based on 500 simulations for each sample size (1000 for sparse k-means). The percentage of models selecting each number of clusters is based on only those data sets for which any variables were selected for clustering.

Approach	N	ARI (95% CI)	Number of Clusters (%)
			1	2	3	4	5	6
VSCC+MVN	200	0.599(0.585,0.612)	0.2	41.8	48.2	7.8	1.4	0.6
	500	0.589(0.578,0.600)	0.0	38.0	28.8	26.2	6.0	1.0
	800	0.515(0.504,0.525)	0.0	24.6	11.2	36.0	23.0	5.2
VSCC+MSN	200	0.556(0.543,0.568)	11.6	82.6	5.8	0.0	0.0	0.0
	500	0.569(0.559,0.579)	0.8	81.6	15.4	2.2	0.0	0.0
	800	0.558(0.546,0.569)	0.0	71.0	21.4	6.8	0.8	0.0
clustvarsel+MVN	200	0.473(0.460,0.486)	0.0	9.0	49.8	34.2	6.0	1.0
	500	0.372(0.362,0.382)	0.0	0.0	1.8	35.2	37.6	25.4
	800	0.359(0.351,0.366)	0.0	0.0	0.0	7.6	39.2	53.2
clustvarsel+MSN	200	0.512(0.497,0.527)	0.2	68.2	29.6	1.6	0.4	0.0
	500	0.498(0.484,0.512)	0.0	23.8	55.2	18.6	2.4	0.0
	800	0.458(0.445,0.471)	0.0	5.2	39.8	39.8	11.2	4.0
clustvarsel+CFUST	200	0.574(0.563,0.585)	9.4	86.0	4.0	0.60	0.0	0.0
skewvarsel+MVN	200	0.560(0.547,0.574)	0.0	21.93	51.51	25.35	1.01	0.20
	500	0.517(0.507,0.527)	0.0	0.6	11.4	72.2	14.6	1.2
	800	0.526(0.520,0.533)	0.0	0.0	3.4	78.4	15.4	2.8
skewvarsel+MSN	200	0.595(0.584,0.605)	0.20	87.12	12.27	0.40	0.0	0.0
	500	0.702(0.693,0.711)	0.0	49.6	49.6	0.8	0.0	0.0
	800	0.762(0.755,0.768)	0.0	16.0	79.0	4.8	0.2	0.0
skewvarsel+CFUST	200	0.615(0.607,0.623)	24.4	73.8	1.2	0.0	0.0	0.0
PGMM	200	0.608(0.598,0.617)	0.0	67.6	27.2	1.8	1.2	2.2
	500	0.650(0.639,0.660)	0.0	33.8	43.8	18.8	3.6	0.0
	800	0.584(0.569,0.598)	0.0	9.0	35.0	28.6	22.2	5.2
sparse k-means	200	0.392 (0.377, 0.408)	63.4	16.0	15.0	4.9	0.7	0.0
	500	0.425 (0.410, 0.440)	50.5	11.8	27.6	7.0	2.9	0.2
	800	0.420 (0.406, 0.434)	42.3	12.5	33.2	6.8	4.8	0.4

Figure 2:

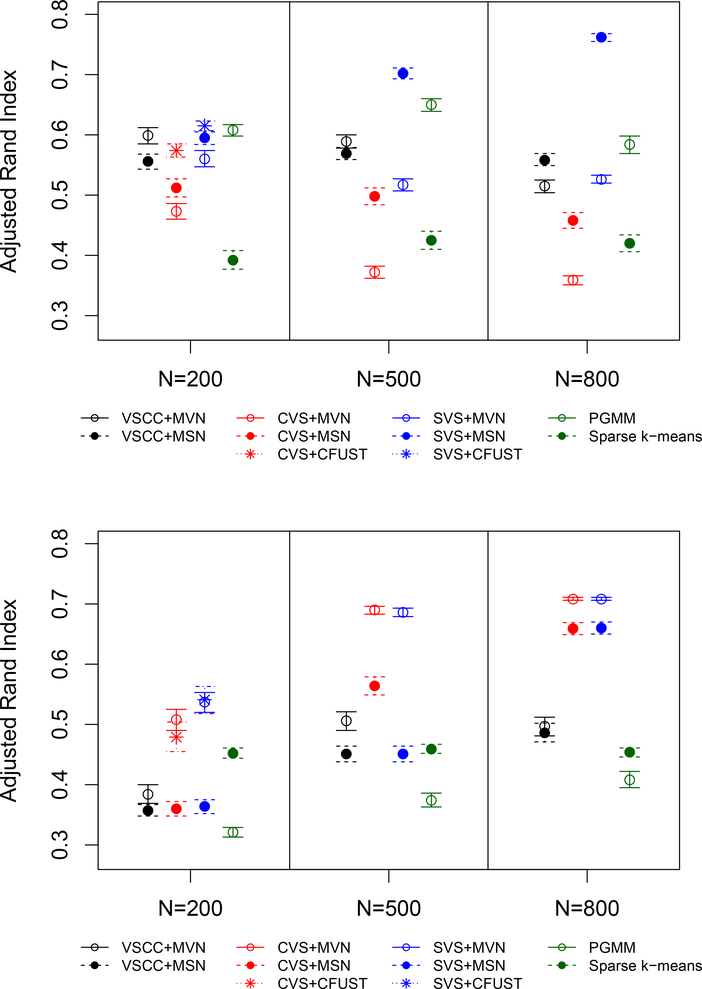
Adjusted Rand Index (ARI) and 95% confidence interval for each clustering strategy in the MSN (top) and MVN (bottom) scenarios. Results are based on 500 simulated data sets (1000 for sparse k-means). The ARI was only calculated if > 1 cluster was detected.

With N = 200, the skewvarsel+CFUST approach (i.e., fitting a CFUST mixture model to variables selected through skewvarsel) and the PGMM approach had the best performances, with ARIs > 0.60. However, both of these approaches suggested only two (rather than the correct three) clusters the majority of the time. The vscc and skewvarsel approaches followed by MSN or MVN clustering and the clustvarsel+CFUST approach resulted in ARIs between approximately 0.55 to 0.60. The clustvarsel+MVN, clustvarsel+MSN, and sparse k-means approaches had the poorest performances, with ARIs < 0.55.

With N = 500 and N = 800, the skewvarsel+MSN approach resulted in the largest ARIs. Notably, with N = 800 it produced an ARI of 0.762 (0.755, 0.768) and correctly identified three clusters in 79% of the simulations. We did not fit the CFUST mixture model for these larger sample sizes because of the computational burden; however based on findings from the N = 200 scenario we expect the skewvarsel+CFUST strategy would also have performed well. The skewvarsel+MVN, vscc+MSN, vscc+MVN, clustvarsel+CFUST, and PGMM approaches performed relatively well, with ARIs > 0.50. Notably, PGMM reached moderate cluster recovery with an ARI of 0.650 (0.639, 0.660) for N = 500, although it only selected the correct number of clusters in 44% of the simulations. The clustvarsel+MVN, clustvarsel+MSN, and sparse k-means approaches performed poorly, with ARIs < 0.50. Notably, the performance of clustvarsel decreased with larger N, and when followed by MVN clustering it typically identified too many clusters.

2.8.2. MVN Clusters (Table 6; Figure 2)

Table 6:

Results from the MVN cluster scenario based on 500 simulations for each sample size (1000 for sparse k-means). The percentage of models selecting each number of clusters is based on only those data sets for which any variables were selected for clustering.

Approach	N	ARI (95% CI)	Number of Clusters (%)
			1	2	3	4	5	6
vscc+MVN	200	0.384(0.369,0.400)	0.0	54.8	29.2	12.6	3.4	0.0
	500	0.506(0.490,0.521)	0.0	39.0	52.4	6.6	1.6	0.4
	800	0.497(0.481,0.512)	0.0	49.6	45.4	3.8	1.0	0.2
vscc+MSN	200	0.357(0.348,0.367)	0.2	93.4	6.4	0.0	0.0	0.0
	500	0.451(0.438,0.464)	0.0	59.4	39.6	1.0	0.0	0.0
	800	0.486(0.471,0.502)	0.0	46.4	50.2	3.4	0.0	0.0
clustvarsel+MVN	200	0.508(0.490,0.525)	0.0	47.2	48.4	4.2	0.2	0.0
	500	0.690(0.683,0.696)	0.0	2.4	96.8	0.6	0.2	0.0
	800	0.708(0.706,0.711)	0.0	0.0	99.8	0.2	0.0	0.0
clustvarsel+MSN	200	0.360(0.348,0.372)	0.0	87.0	13.0	0.0	0.0	0.0
	500	0.564(0.549,0.579)	0.0	31.8	67.8	0.4	0.0	0.0
	800	0.659(0.649,0.669)	0.0	8.6	90.6	0.8	0.0	0.0
clustvarsel+CFUST	200	0.479(0.455,0.504)	61.8	17.4	20.2	0.6	0.0	0.0
skewvarsel+MVN	200	0.537(0.520,0.553)	0.0	39.2	56.0	4.4	0.4	0.0
	500	0.686(0.679,0.693)	0.0	3.2	96.0	0.6	0.0	0.2
	800	0.708(0.706,0.711)	0.0	0.0	99.8	0.2	0.0	0.0
skewvarsel+MSN	200	0.364(0.352,0.375)	0.0	86.4	13.6	0.0	0.0	0.0
	500	0.451(0.438,0.464)	0.0	59.4	39.6	1.0	0.0	0.0
	800	0.660(0.650,0.670)	0.0	8.8	90.2	1.0	0.0	0.0
skewvarsel+CFUST	200	0.541(0.518,0.563)	66.8	9.6	23.2	0.4	0.0	0.0
PGMM	200	0.321(0.313,0.329)	0.0	91.4	4.4	1.8	1.0	1.4
	500	0.374(0.363,0.386)	0.0	82.8	11.6	4.4	1.2	0.0
	800	0.408(0.395,0.422)	0.0	75.8	17.4	3.0	3.6	0.2
sparse k-means	200	0.452 (0.444, 0.461)	47.6	21.9	27.5	2.7	0.3	0.0
	500	0.459 (0.452, 0.467)	34.6	13.2	46.4	5.0	0.8	0.0
	800	0.454 (0.446, 0.461)	26.9	11.9	52.4	7.4	1.3	0.1

With N = 200, the clustvarsel+MVN, skewvarsel+CFUST, and skewvarsel+MVN approaches had the best performances, with ARIs > 0.50. clustvarsel+MVN and skewvarsel+MVN tended to select two or three clusters, while skewvarsel+CFUST tended to only select one cluster. Sparse k-means and clustvarsel+CFUST had ARIs between 0.45 and 0.50 and tended to select one cluster. The remaining approaches all had ARIs < 0.50.

With N = 500, clustvarsel+MVN and skewvarsel+MVN performed very well, with ARIs > 0.65 and correct identification of three clusters for over 95% of the simulated data sets. clustvarsel+MSN and vscc+MVN had ARIs > 0.50 and most often selected three clusters. The remaining approaches had ARIs < 0.50.

With N = 800, all clustvarsel and skewvarsel approaches performed well, with ARI’s > 0.65 and correct identification of 3 clusters for > 90% of simulated data sets. Notably, both skewvarsel+MVN and clustvarsel+MVN identified three clusters in 99.8% of simulated data sets. The vscc approaches had ARIs slightly below 0.50 and tended to select two or three clusters. The two implicit approaches (PGMM and sparse k-means) performed poorly, with ARIs between approximately 0.40 to 0.45.

3. AgeWise Application

We applied mixture models the AgeWise data (Buysse et al., 2011) to reveal novel, clinically meaningful subgroups based on sleep characteristics captured through Diary, ACT, and PSG data types. Because of prior findings indicating the importance of sleep discrepancies across data types (Kay et al., 2015; Lund et al., 2013; Baillet et al., 2016), our particular clinical interest was in using a set of variables for clustering that included at least one of each of the Diary, ACT, and PSG variables. To accomplish this, we applied our proposed skewvarsel-p variable selection algorithm, which assumes skewed clusters and suggests multiple statistically plausible sets of variables that each incorpo-rate Diary, ACT, and PSG variables. For comparison purposes we also applied our proposed MSN-based skewvarsel variable selection algorithm and the MVN-based analogue clustvarsel (Scrucca and Raftery, 2014). For each set of variables suggested, we applied mixture models based on three different distributions (MVN, MSN, CFUST) and selected the final clustering solution based on the BIC.

For variable selection, we considered 1 − 6 clusters, allowed for all available covariance patterns, and required a BIC difference of −10 to enter or remove a variable. For subsequent mixture modeling, we used a maximum of 1000 EM iterations with a tolerance of 10⁻⁶. Because the CFUST model is particularly dependent on initial values, we generated initial values from both “restricted” and “unrestricted” skew t-distributions, the latter of which was fit with the fmmst function from the EMMIXuskew package (Lee and McLachlan, 2013a) in R. All other analyses were performed using the the R functions and packages described in Table 3.

3.1. Results from the skewvarsel-p Algorithm

Table 7 shows the six sets of variables revealed by the skewvarsel-p algorithm, one for each permutation of the Diary, ACT, and PSG data types. After examining all six sets, we selected the set indicated by both the Diary-ACT-PSG and Diary-PSG-ACT permutations for further examination. This set consisted of: (1) standard deviation of Diary Sleep Latency [sdSL(D)]; (2) mean of ACT SL [SL(A)]; (3) mean of PSG SL [SL(P)]; (4) mean of Diary SL [SL(D)]; and (5) mean of PSG NREM [NREM(P)]. Because this set was selected by two permutations, it suggests a more stable clustering solution. Moreover, it is clinically relevant because this set contains self-report, behavioral, and physiological homologues of SL. SL has been associated with numerous medical and psychological outcomes, and the exploration of differences and similarities of SL variables within each subgroup has the potential to produce clinically meaningful findings (Vgontzas et al., 2013; Troxel et al., 2010, 2012; Dew et al., 2003).

Table 7:

Variable selection and clustering results based on AgeWise data. For the skewvarsel-p algorithm, the specific permutation of data types is provided in parentheses, where P=PSG, A=Actigraphy, and D=Diary. Variables represent averages over multiple nights of observation unless prefixed with “sd”, in which case they represent the standard deviation. The P, A, or D in parentheses after each variable indicates the data source through which it was measured. See Table 1 for full variable descriptions and abbreviations.

Algorithm	Variables Selected	Skewness Rankings	Spearman r Median (Min., Max)	Cluster Distribution	Number of Clusters
clustvarsel	SL(P), sdSL(D), SL(D), SL(A), RL(P), RLA(P)	5,14,7,6,20	0.07(0.003,0.93)	CFUST	2
skewvarsel	%Delta(P), Delta(P), Bed(P)	30,28,60	0.05(0.02,0.99)	MSN	4
skewvarsel-p(PDA)	%Delta(P), sdMood(D), sdSE(A), Delta(P), TST(P)	30,43,4,28,56	0.16(0.002,0.99)	CFUST	4
skewvarsel-p(PAD)	%Delta(P), sdSL(A), sdSL(D), Delta(P), SL(D), TST(P)	30,9,14,28,6,56	0.15(0.07,0.83)	CFUST	3
skewvarsel-p(APD)	SL(A), %Delta(P), sdWASO(D), Delta(P)	6,30,21,28	0.13(0.03,0.99)	CFUST	2
skewvarsel-p(DAP)	sdSL(D), SL(A), SL(P), SL(D), NREM(P)	14,6,5,6,67	0.19(0.05,0.83)	CFUST	2
skewvarsel-p(DPA)	sdSL(D), SL(P), SL(A), SL(D), NREM(P)	14,6,5,6,67	0.19(0.05,0.83)	CFUST	2
skewvarsel-p(ADP)	SL(A), sdWASO(D), N2(P), sdSL(A)	6,21,70,9	0.20(0.03,0.92)	CFUST	2

The BIC indicated that the CFUST mixture model with two clusters was the best fit for this selected set of variables. Clusters are illustrated in Figure 3 and further characterized in Table 8. Individuals in cluster 1 (N₁ = 140) were generally better sleepers than those in cluster 2 (N₂ = 76), with lower SL across all data sources (i.e., fewer minutes to fall asleep) and more non-REM sleep. Overall, these findings emphasize the importance of studying SL across multiple data types in future research. Finally, although individuals in cluster 1 were “better” sleepers than those in cluster 2, approximately half were diagnosed with insomnia (compared to approximately three-quarters in cluster 2). This disconnect between cluster (based on Diary, ACT, and PSG) and insomnia diagnosis (based on Diary and clinical interviews) highlights how clustering on multiple data types can clarify heterogeneity beyond the presence or absence of a diagnosis based only on self-report.

Figure 3:

CFUST clustering results based on variables selected through the Diary-ACTPSG and Diary-PSG-ACT permutations of the skewvarsel-p algorithm. Black circles represent the “Lower Sleep Latency (SL)” cluster. Red triangles represent the “Higher SL” cluster.

Table 8:

Cluster characteristics based on variables selected through the skewvarsel-p algorithm, with clusters revealed using a CFUST mixture model. Effect sizes are Cohen’s d for continuous measures and risk difference for categorical measures. Variables represent the averages of multiple nights of observation unless prefixed with “sd”, in which case they represent the standard deviation. The P, A, or D in parentheses after each variable indicates the data source (PSG, ACT, or Diary) through which it was measured. Table 1 provides full variable descriptions and abbreviations.

	Lower SL C1(N = 140)	Higher SL C2(N = 76)	Effect Size
Sleep Characteristics for Clustering
sdSL(D)	6.81(3.62,12.81)	33.68(18.95,63.33)	0.62
SL (A)	13.45(7.14,21.31)	36.43(26.1,62.04)	0.63
SL (P)	8.12(4.63,14.12)	13.96(9.73,19.99)	0.33
SL (D)	10(6.46,16.5)	18.33(9.46,38.5)	0.34
NREM (P)	289(245.38,329)	268.17(239.34,299)	−0.15
Additional Sleep Characteristics
WASO (D)	32.64(9.14,61.17)	39.09(23.3,65)	0.10
WASO (A)	45.39(29,60)	53.25(37.47,66.93)	0.17
WASO (P)	68.16(44.5,98.75)	82.33(51.08,126.17)	0.13
TST (D)	380.62(339.88,436.87)	351.62(309.64,385.52)	−0.25
TST (A)	396.5(359.57,433.55)	395.07(356.23,435.07)	0.01
TST (P)	371(327,406.92)	349.59(309.5,390.62)	−0.15
Quality (D)	62.22(51.13,78.65)	53.81(47.11,65.45)	−0.20
% Stage N3 (P)	3.87(1.07,12.1)	4.1(0.55,9.78)	−0.07
Clinical and Demographic Characteristics
Insomnia dx (%,n)	53.6(75)	75.0(57)	0.21
Age	69.15(64.32,75.31)	70.08(65.5,76.21)	0.09
Female (%,n)	69.3(97)	73.7(56)	0.04
White (%,n)	92.8(128)	89.2(66)	−0.04

Finally, we note that by considering all permutations we were able to explore six po-tential solutions, each containing Diary, ACT, and PSG, and select the one that was most clinically meaningful. Had we only considered one permutation (e.g., selected the first variable to be the one of any data type with the strongest evidence of univariate clustering, selected the second variable to be the one out of remaining data types with the strongest evidence of bivariate clustering, and so on) we would have only been able to consider the solution from the set of variables indicated in the SVS-p(PAD) permutation. This set is not as clinically useful as the one we selected because it does not contain all three homologues of SL. However, in further research this would also be an important solution to investigate further.

3.2. Comparison Across Different Sets of Clustering Variables

As shown in Table 9, the seven unique sets of variables produced very different clustering solutions, with ARIs ranging from -0.008 to 0.477. These different clustering solutions emphasize how there can be multiple statistically plausible ways to cluster the sample depending on which variable set is considered. Table 9 also highlights how the subgroups revealed through clustering on multiple data types provide entirely different information than the insomnia diagnosis based only on self-report. Thus, there is a great deal of heterogeneity in this sample beyond that which can be explained by self-report alone. This finding lends credence to the NIMH’s call for clarifying the boundaries of existing diagnoses by integrating data from multiple data sources (Insel et al., 2010; Casey et al., 2013; Cuthbert and Insel, 2013).

Table 9:

Comparisons of final clustering solutions and the insomnia diagnosis based on the Adjusted Rand Index. CVS indicates the clustvarsel algorithm, SVS indicates the skewvarsel algorithm, and SVS-p indicates the skewvarsel-p algorithm. For skewvarsel-p, the specific permutation of data types is provided in parentheses, where P=PSG, A=Actigraphy, and D=Diary.

	SVS	SVS-p(PDA)	SVS-p(PAD)	SVS-p(APD)	SVS-p(DAP/DPA)	SVS-p(ADP)	Insomnia
CVS	−0.011	−0.005	−0.002	−0.005	0.025	−0.004	−0.008
SVS	1.000	0.260	0.477	0.395	0.002	0.004	−0.005
SVS-p(PDA)		1.000	0.298	0.456	0.0001	0.026	0.005
SVS-p(PAD)			1.000	0.347	0.018	0.032	−0.005
SVS-p(APD)				1.000	0.016	0.023	0.0001
SVS-p(DAP/DPA)					1.000	0.067	0.009
SVS-p(ADP)						1.000	0.020

4. Discussion

We presented two exploratory variable selection methods for skewed model-based clustering. The first, skewvarsel, uses a stepwise algorithm to reveal a subset of variables that is useful for skewed clustering. The second, skewvarsel-p, is also based on a stepwise algorithm but suggests multiple plausible sets of variables for skewed clustering that each incorporate data captured across multiple data types. The second method is motivated by the National Institute of Mental Health Research Domain Criteria (RDoC) framework, which calls for the identification of novel and clinically meaningful phenotypes based on data from multiple levels of information (i.e., self-report, behavior, and physiology, circuits, molecules, cells, and/or genes), as well as our own a priori hypotheses regarding the importance of similarities and discrepancies across data types in sleep research.

Our simulation study indicated that skewvarsel is a promising approach for selecting an explicit subset of clustering variables, especially with large sample sizes (N ≥ 500). When underlying clusters were skewed, skewvarsel was more accurate in selecting the correct subset of variables than either vscc or clustvarsel variable selection algorithms, which are based on underlying assumptions of normality. vscc consistently selected too many variables, and clustvarsel gravitated towards selecting the most highly skewed variables, regardless of whether they were actually useful for clustering. Moreover, when underlying clusters were normally distributed, our skewvarsel algorithm performed at least as well as clustvarsel and better than vscc. When underlying clustering are skewed, applying a more flexible mixture model distribution such as the CFUST (Lee and McLachlan, 2016b) to variables selected through either skewvarsel or clustvarsel may improve the accuracy of the final clustering solution.

Our simulation also evaluated two implicit dimension reduction approaches: sparse kmeans clustering and parsimonious Gaussian mixture models (PGMM). With MSN clusters and N = 200, the level of cluster recovery obtained through PGMM was competitive with mixture models fit to variables selected through skewvarsel. With larger sample sizes, PGMM lagged behind the MSN mixture models fit to variables selected through skewvarsel. However, PGMM performed at least as well as the MVN mixture models fit to variables selected through skewvarsel. Somewhat surprisingly, neither of the implicit approaches performed particularly well in the MVN scenario, where skewed variables were mixtures of MVN clusters. When considering these findings, it is important to note that data were generated with an underlying assumption of an explicit subset of variables being useful for either MVN or MSN clustering. Moreover, our simulation was based on only six variables, which may favor explicit variable selection methods over implicit dimension reduction. In future work it will be important to further compare explicit variable selection and implicit dimension reduction techniques in both lower and higher dimensional data. It will also be important to evaluate other implicit dimension reduction approaches, including mixtures of factor analyzers based on the generalized hyperbolic (Tortora et al., 2016), skew normal (Lin et al., 2016), and skew t (Murray et al., 2014a,b; Lin et al., 2015) distributions.

When data are skewed, one may also consider transforming the data prior to applying a MVN-based variable selection algorithm and mixture model. Given the pervasiveness of skewed data in sleep research, such transformations are commonly used (e.g., see Tarokh et al. 2011; Borodulin et al. 2009). However, the goal of clustering is to explain the natural heterogeneity in a sample, and a transformation inherently alters this natural heterogeneity. For example, a log transformation stretches out values in the range of (0 − 1] and contracts values in the range (1,∞). Consistent with Schork et al. (1990), we argue that the skewness observed in a distribution is a fundamental trait, and thus, transforming the data to remove this skewness has the potential to remove the most interesting aspect of the data. However, others contend that a well-thought-out transformation prior to clustering may improve results (Yeung et al., 2001), and mixture models that incorporate the Box-Cox transformation within the algorithm have even been proposed (Lo and Gottardo, 2012). As such, the use of transformations prior to clustering remains a topic under debate.

Computation time for the skewvarsel algorithm varies based on sample size and the number of variables considered. In the MSN simulation scenario (6 variables) the mean(SD) minutes to run the skewvarsel algorithm was 6.90(1.00) for N = 200, 18.90(0.46) for N = 500, and 29.45(0.62) for N = 800. In the MVN simulation scenario (6 variables) the mean(SD) minutes to run the skewvarsel algorithm was 7.20(0.47) for N = 200, 18.30(0.30) for N = 500, and 28.97(0.17) for N = 800. In the application section (70 variables, N = 216), the six permutations from the skewvarsel-p algorithm had computational times of 55 minutes (ADP), 79 minutes (APD), 109 minutes (PDA), 110 minutes (PAD), 74 minutes (DAP), and 75 minutes (DPA). The skewvarsel algorithm had a computational time of 78 minutes. These times could be substantially reduced if model-fitting were parallelized within the algorithm. While these times are not unreasonable in the context of skewed clustering, we note that they are substantially (i.e., approximately 100–200 times) slower than the clustvarsel algorithm.

Our findings should be considered in the context of some limitations. The AgeWise sample of N = 216 may be somewhat small for the proposed method, as indicated by our simulation study findings. The methods should be applied to a larger and independent sample to validate our findings. In addition, the current algorithm is based on the MSN distribution, which is one of the more restrictive asymmetric distributions. We used this distribution in part because efficient, computational tools were readily available. Ideally, the suitability of the distribution for the data at hand, and not the availability of easy computational tools, should be the primary consideration for selecting a distribution. The proposed methods can and should be extended to other, more flexible distributions that allow for asymmetry, including methods for combining MVN mixture components (Hennig, 2010; Baudry et al., 2010).

A limitation of the simulation study is that we set a maximum of 1000 iterations for some model-based clustering approaches. This setting had the potential to be most limiting for the highly parameterized CFUST model. For the MSN cluster scenario with N = 200, 284/500 skewvarsel+CFUST models had not converged at a tolerance of 10⁻⁵ by 1000 iterations. Even so, the median (Q1, Q3) convergence for these models was 0.0002(0.0001, 0.0006). Because these models were close to converging at the 10⁻⁵ criterion, we expect that setting a maximum of 1000 iterations had only a minor impact on the results.

In conclusion, this research highlights the need to consider skewed variable selection and mixture model approaches in applied sleep research, where investigators commonly capture sleep through self-reported (Diary), behavioral (ACT), and physiological (PSG) measures. However, the methods presented herein are generalizable to other areas of application as well. For example, skewed data are also common in genetics (Yeung et al., 2001; Eisen et al., 1998) and biological marker research (Reinke et al., 2014; Fakhry et al., 2013; Hlebowics et al., 2011; Bafadhel et al., 2011), as evidenced by the common use of log and square root transformations in practice. These types of data are of central interest in the NIMH RDoC initiative, and we expect that applying our methods in these areas will move researchers closer to clarifying the heterogeneity observed in diagnoses based on self-report, revealing underlying disease mechanisms, and generating hypotheses for personalized treatments.