Large field of view distortion assessment in a low‐field MR‐linac

Abstract

Purpose

MR‐guided radiation therapy (RT) offers unparalleled soft tissue contrast for localization and target tracking. However, MRI distortions may be detrimental to high precision RT. This work characterizes the gradient nonlinearity (GNL) and total distortions over the first year of clinical operation of a 0.35T MR‐linac.

Methods

For GNL characterization, an in‐house large field of view (FOV) phantom (60 × 42.5 × 55 cm³, >6000 spherical landmarks) was configured and scanned at four timepoints with forward/reverse read polarities (Gradient Echo sequence, FA/TR/TE = 28°/30 ms/6 ms). GNL was measured in Anterior‐Posterior (AP), Left‐Right (LR), and Superior‐Inferior (SI) frequency‐encoding directions based on deviation of the auto‐segmented landmark centroids between rigidly registered MR and CT images and assessed based on radial distance from magnet isocenter. Total distortion was assessed using a 30 × 30 cm² grid phantom oriented along the cardinal axes over >1 year of operation.

Results

The scanner's spatial integrity within the first ~10 months was stable (maximum total distortion variation = 10/6/8%, maximum distortion = 1.41/0.99/1.56 mm in Axial/Coronal/Sagittal planes, respectively). GNL distortions measured during this time period <10 cm from isocenter were (−0.74, 0.45), (−0.67, 0.53), and (−0.86, 0.70) mm in AP/LR/SI directions. In the 10‐20 cm range, <1.5% of the distortions exceeded 2 mm in the AP and LR axes while <4% of the distortions exceeded 2 mm for SI. After major repairs and magnet re‐shim, detectable changes were observed in total and GNL distortions (20% reduction in AP and 36% increase in SI direction in the 20–25 cm range). Across all timepoints and axes, 38–53% of landmarks in the 20–25 cm range were displaced by >1 mm.

Conclusions

GNL distortions were negligible within a 10 cm radius from isocenter. However, in the periphery, non‐negligible distortions of up to ~7 mm were observed, which may necessitate GNL corrections for MR‐IGRT for treatment sites distant from magnet isocenter.

1. Introduction

Magnetic resonance image‐guided radiation therapy (MR‐IGRT) offers simultaneous tracking of the target during treatment delivery while taking advantage of the excellent soft tissue contrast of MRI.¹ Even at low magnetic field strengths such as 0.35T, visualization of tissues and most critical structures is superior to cone beam CT (CBCT).² Also, the use of MR‐IGRT can avoid the additional radiation exposure that is inherent to CBCT¹ and therefore, can enable daily monitoring of intra‐fractional motion as well as treatment plan adjustments based on changes in anatomy.³ Recently, MRI has been coupled with a linear accelerator (MR‐linac) offering possibilities such as treatment of small brain metastases in an MR‐guided stereotactic radiosurgery (MRgSRS) setting.^{4, 5, 6, 7} However, as with any MR imaging system, one of the challenges in MR‐IGRT is dealing with distortions that are intrinsic to MRI.⁸ Geometric distortions can lead to target localization uncertainties, which can lead to missing or underdosing the target during treatment.^{9, 10} For high fidelity MR‐IGRT, spatial accuracy is of critical importance for accurate treatment execution, thus characterization of these geometric distortions is particularly necessary.

The major sources of distortion in MRI arise from static field inhomogeneity, magnetic susceptibility, chemical shift, and spatial‐encoding gradient nonlinearity (GNL).^{8, 11} Subject‐specific distortions are mainly due to the chemical shift and magnetic susceptibility^{12, 13, 14} while GNL and field inhomogeneity are system‐specific causes of distortion. Several factors such as type and field strength of the MR scanner, imaging sequence, and receiver bandwidth can influence the magnitude of distortions from one or more of these sources.^{15, 16, 17} It has been shown that at low magnetic field strengths, effects of susceptibility and chemical shift are negligible.¹¹ GNL is one of the major contributors to spatial distortion, which is independent of subject and imaging sequence.¹⁸ Furthermore, for most diagnostic MRI scanners and MR simulators (MR‐SIMs), distortion magnitude increases as the distance from magnet isocenter increases.^{19, 20, 21} Several phantom‐based methods have been developed for measurement and correction of GNL effects.^{21, 22, 23, 24} While we have previously reported characterization of GNL at varied MRI field strengths using a modular in‐house large field of view (FOV) phantom,²⁵ the characterization and understanding of GNL for MR‐IGRT is currently limited. This work sought to characterize the GNL distortion across a large FOV for a 0.35T MR‐linac, with the overarching goal of quantifying the GNL to assess the necessity of correcting GNL‐based distortions for MRI‐only planning in an MR‐IGRT clinical workflow.

2. Materials and methods

2.A. MR‐linac and phantom configuration

All measurements were conducted on the MRIdian Linac (ViewRay, Mountain View, CA, USA) with a double‐donut superconducting wide bore (70 cm diameter) magnet with 0.35T field strength (50 cm FOV) and a 6 MV flattening filter‐free linac. The system is comprised of five cylindrical ferromagnetic compartments around a magnetically shielded ring located between the double donuts to minimize magnetic field interference. After installation, the GNL of the MR gradient system was characterized by the vendor via simulations to characterize the coefficients of the spherical harmonic polynomials. To compensate for the MR gradient coil impurities, spherical harmonics coefficients up to the 10th order for the x, y, and z gradient coils were obtained for >50 cm DSV and optimized via an iterative calibration procedure. Coefficients were then translated into the online 3D distortion correction integrated into image reconstruction by Siemens (MAGNETOM Avanto, Syngo MR B19). An in‐house modular large FOV phantom was configured to fit the magnet bore. The details of phantom design and implementation have been previously reported.^{25, 26} Briefly, the phantom is constructed of layers of low‐density polyurethane foam boards (6 lbs/ft³, 2.5 cm thick) with each board consisting of linear arrays of 6 mm diameter paintballs spaced 2.5 cm apart for signal generation. The phantom's external alignment marks were aligned to the room lasers and the plates were configured to fill the magnet bore as shown in Fig. 1(a).

Figure 1.

(a) Large field of view distortion phantom configured to fit the 0.35T magnet bore. Axial phantom views of the CT image at (b) the isocenter and planes shown in the inferior direction at (c) 5 cm (d) 10 cm (e) 15 cm, and (f) 20 cm from the isocenter. Similar patterns were observed at planes superior to the magnet isocenter. The landmarks demonstrate gradient nonlinearity (GNL) distortions of the MR image isolated along the y‐axis measured using the reverse gradient method (AP gradient encoding) showing the highest magnitude among the three directions studied. The resulting GNL distortion is the residual distortion after vendor supplied corrections were applied. [Color figure can be viewed at wileyonlinelibrary.com]

2.B. Image acquisition

Computed tomography (CT) datasets were acquired to serve as the distortion‐free reference condition at 120 kVp on a Philips Brilliance Big Bore (Philips Healthcare, Best, the Netherlands) with a voxel size of 1.17 × 1.17 × 1 mm³ and FOV of 600 × 600 × 600 mm³. While the overall geometric distortion in MRI is the superposition of effects of GNL, inhomogeneity of the B₀ field, and magnetic susceptibility, GNL can be isolated using a well‐established reverse gradient technique.^{11, 27} When acquiring images based on the reverse gradient method, by reversing the polarity of the read gradient, the polarity of the B₀ and susceptibility distortions are reversed while the polarity of the gradient distortions do not change.²⁷ Thus, for each of the x, y, and z gradients, the phantom was scanned once with positive and once with negative read encode gradients to represent the [Left‐Right (LR), Right‐Left (RL)], [Anterior‐Posterior (AP), Posterior‐Anterior (PA)], and [Superior‐Inferior (SI), Inferior‐Superior (IS)] orientations in the bore coordinates, respectively. MR images for measuring the x and y gradient coil nonlinearity were acquired in axial planes and for the z gradient coil in sagittal planes(3D Gradient Echo, Repetition Time (TR)/Echo Time (TE) = 30/6 ms, Flip Angle (FA) = 28°, Bandwidth = 260 Hz/pixel, FOV = 540 × 540 × 528 mm³, Voxel size = 1.54 × 1.54 × 1.5 mm³, single channel transmit/receive body coil). While other sequences, such as a 3D spin echo (3DSE) or other weightings could have been used, a 3DSE or T2‐weighted acquisition would have required substantially longer scan times than 3DGRE. Our selection of T1‐weighted 3DGRE is also consistent with the literature to enable more direct comparison.^{11, 27, 28} It is important to note that all analysis was performed after vendor‐supplied 3D geometry correction was applied to isolate postcorrection residual distortion.

To assess the temporal stability of the GNL assessment, acquisition was performed at 2, 8, 10, and 14 months from the start of the MR‐linac operation to characterize GNL three to four timepoints depending on the axis of acquisition. Acquisition of the CT image was also repeated at each timepoint to provide an up‐to‐date reference condition for the phantom.

2.C. Gradient nonlinearity image processing and analysis

To establish a mutual coordinate system, MR image volumes were rigidly registered to the reference CT image with 6 degrees of freedom and normalized mutual information as the cost function, using FSL²⁹ (FMRIB Software Library, Wellcome Centre For Integrative Neuroimaging, Oxford, UK). To minimize the impact of the GNL on establishing the frame of reference, only landmarks within a 15 ×15 × 15 cm³ box around the magnet isocenter were used for rigid alignment. To quantify registration accuracy, MR/CT registrations were repeated 5 times for each timepoint/axis combination, and the displacement between the MRI and CT landmark centroids located at isocenter was calculated.

For GNL distortion quantification, all image processing was conducted in MATLAB^® R2016b (Mathworks, Natik, MA, USA). Background noise in CT and MR images was removed by applying a Gaussian blur followed by a rolling ball algorithm.³⁰ Landmarks were first segmented by thresholding the image and then isolated using the connectivity of the 26 neighboring voxels belonging to each landmark.³¹ To measure distortion in each image, landmark centroids were identified in the CT image and MR images. The distortion at the landmark location in each GRE image was measured by calculating the displacement of the centroid along the frequency‐encoding direction with reference to its position in the reference CT image. By averaging the measured displacement of the landmarks in the forward and reverse gradient polarity images, isolated GNL distortion was then determined from the location of each landmark. This procedure was done for the LR‐RL, AP‐PA, and SI‐IS GRE images to measure GNL distortion along the x, y, and z axes, respectively, for all landmarks out to a maximum of 25 cm from magnet isocenter.

The mean and standard deviation of the GNL distortions were calculated for all landmarks within three radial distances (0–10 cm, 10–20 cm, and 20–25 cm) from the magnet isocenter. To avoid the impact of single landmarks, the 1% (P1) and 99% (P99) percentiles of all measured values were calculated in lieu of minimum and maximum to examine the overall range of distortions. To evaluate GNL stability over time, the standard deviation (SD) of distortions within each of the three radial ranges from the isocenter was calculated and compared between timepoints.

2.D. Routine assessment of MRI spatial integrity

Routine MRI spatial distortion arising from all system‐ and object‐induced distortions of a clinical sequence (termed “total distortion”) was assessed monthly and after major equipment repairs over a period of 15 months. A rectangular box phantom (Fluke Biomedical, model 76‐907, signal‐generating solution containing ~400 cylindrical objects spaced 1.45 cm apart in a ~30 × 30 cm² area^{32, 33}) was imaged using a 3D gradient, steady‐state sequence (TR/TE/FA = 3.36/1.44 ms/60°, Voxel size = 1.5 × 1.5 × 3.0 mm³). Three images of the phantom were acquired with the long axis of the phantom oriented along the axial, sagittal, and coronal planes. Positional deviations between the cylindrical objects in the acquired images and a binary template were evaluated via vendor supplied, MATLAB‐based software, and the differences were quantified.

3. Results

Fig. 1(a) shows the large FOV GNL phantom configuration optimized to fit the 0.35T magnet bore. The final assembled phantom consisted of 17 plates and a physical size of 600 (width) × 425 (height) × 550 (length) mm³ with ~6300 landmarks covering a spatial volume of 500 × 400 × 500 mm³ within the phantom. Measurement of post‐registration displacement of the centermost landmark between the MR and CT datasets revealed a residual difference of 0.04 ± 0.08 mm, 0.01 ± 0.09 mm, and −0.16 ± 0.11 mm in the LR, AP, and SI directions, respectively, across all acquired image volumes and acquisition timepoints.

Fig. 1(b)–1(f) show axial views of the CT image volume at the central slice and at 5, 10, 15, and 20 cm, respectively, inferiorly from the isocenter, overlaid with corresponding landmarks representing the overall GNL distortions along the y‐axis from the reverse gradient method for the AP frequency‐encoded MRI datasets, highlighting the worst results obtained. The landmark position represents the residual GNL distortion after 2D and 3D vendor supplied corrections were applied. Displacement of the landmarks from their original location (based on the reference CT image) was clearly more pronounced near the phantom periphery. Missing landmarks from the edges of the image occurred when the landmarks shifted outside of the useable FOV and thus these landmarks could not be analyzed. At farther distances from isocenter, the residual GNL distortion increased, most notably as shown in the 15 and 20 cm axial planes where the central landmarks show deviations from the CT dataset.

Fig. 2 highlights the GNL results at four timepoints for each axis. In this figure, each dot represents one landmark and its deviation along the vertical axis is the measured distortion in the LR‐RL, AP‐PA, and SI‐IS directions in the scanner coordinates. Baseline SI‐IS data were lost due to operator error.

Figure 2.

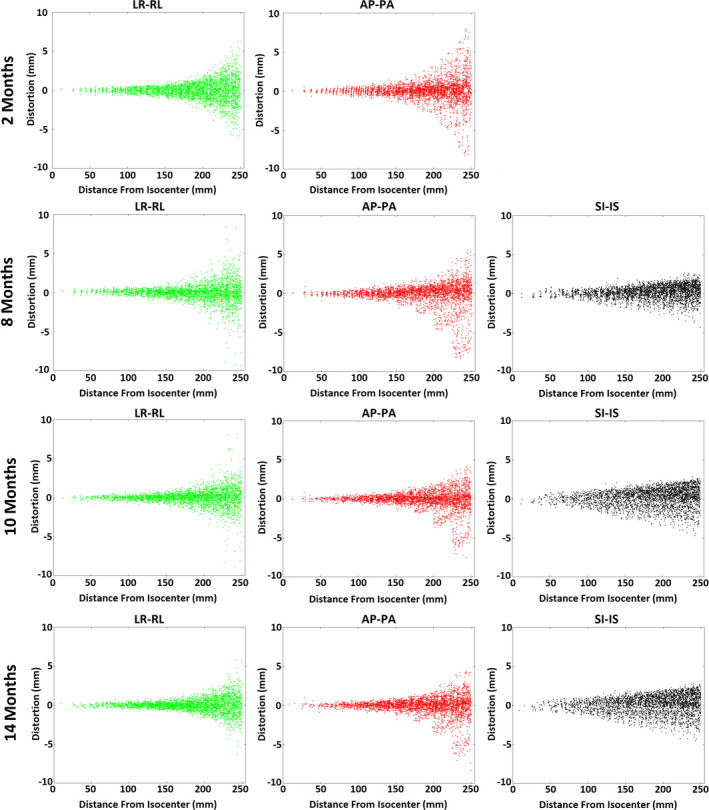
Gradient nonlinearity distortions in the Anterior‐Posterior (AP‐PA), Left‐Right (LR‐RL), and Superior‐Inferior (SI‐IS) directions at distances of 0–25 cm from the magnet isocenter. Plots show distortion measurement results at 2, 8, 10, and 14 months from the start of operation of the MR‐linac. [Color figure can be viewed at wileyonlinelibrary.com]

Table 1 summarizes GNL distortions within the three ranges of 0–10 cm, 10–20 cm, and 20–25 cm from the isocenter as observed in the four measurement timepoints. Notably, virtually all landmarks within 10 cm from the isocenter had a GNL distortion <1 mm in the AP, LR, and SI axes across all timepoints, with the exception of the post‐repair timepoints in the SI axis (3.8% and 1.5% of landmarks yielded distortion >1 mm but all were <2 mm). In the 10–20 cm range, <1.5% of the distortions exceeded 2 mm in the AP and LR axes while <4% of the distortions exceeded 2 mm in the SI axis. As expected, the largest distortions occurred within the 20–25 cm range with absolute displacements of up to ~5 mm and ~7 mm in the LR and AP directions, respectively. In this same region, 3.7–21.6% of the landmarks yielded >2 mm displacement across all timepoints and axes. Although distortion in the SI direction was greater than the other two directions near isocenter, it remained <4 mm within the entire FOV across all timepoints.

Table 1.

Summary statistics of the gradient nonlinearity (GNL) distortions along the Left‐Right (L‐R), Anterior‐Posterior (A‐P), and Superior‐Inferior (S‐I) directions at three radial distances from the magnet isocenter. Table shows mean, standard deviation (SD), percent of measured GNL distortions falling in 1% and 99% percentile of all measured values (P1 and P99, respectively) for each radial distance from magnet isocenter (0–10 cm, 10–20 cm, and 20–25 cm). The percentage of landmarks with GNL distortion greater than ±1 and ±2 mm within the specified range are also reported

Axis	Months	0–10 cm			10–20 cm			20–25 cm
		Mean ± SD [P1, P99]	% >1 mm	% >2 mm	Mean ± SD [P1, P99]	% >1 mm	% >2 mm	Mean ± SD [P1, P99]	% >1 mm	% >2 mm
L‐R	2	−0.01 ± 0.23 [−0.67, 0.53]	0.0	0.0	−0.02 ± 0.56 [−1.35, 1.19]	7.5	0.2	−0.05 ± 1.61 [−4.22, 4.02]	52.6	18.0
	8	0.01 ± 0.22 [−0.48, 0.53]	0.0	0.0	0.02 ± 0.52 [−1.47, 1.51]	5.9	0.6	−0.02 ± 1.64 [−4.83, 4.27]	39.0	15.6
	10	0.00 ± 0.23 [−0.56, 0.55]	0.0	0.0	0.02 ± 0.52 [−1.47, 1.28]	6.5	0.4	0.05 ± 1.50 [−4.19, 3.42]	40.4	12.9
	14	0.01 ± 0.23 [−0.48, 0.50]	0.0	0.0	0.00 ± 0.44 [−1.11, 1.21]	3.3	0.0	−0.01 ± 1.25 [−3.00, 3.10]	40.3	10.2
A‐P	2	0.02 ± 0.27 [−0.74, 0.61]	0.0	0.0	0.00 ± 0.64 [−1.94, 1.74]	10.2	1.5	0.06 ± 1.98 [−6.56, 5.39]	41.1	21.6
	8	−0.02 ± 0.25 [−0.69, 0.45]	0.0	0.0	0.03 ± 0.65 [−2.18, 1.42]	10.1	1.5	−0.23 ± 2.08 [−7.30, 4.07]	43.9	20.9
	10	−0.01 ± 0.22 [−0.62, 0.57]	0.0	0.0	0.02 ± 0.53 [−1.53, 1.30]	7.4	0.0	−0.29 ± 1.67 [−5.73, 3.10]	39.5	17.1
	14	0.01 ± 0.24 [−0.70, 0.57]	0.0	0.0	0.02 ± 0.56 [−1.69, 1.27]	7.5	0.2	−0.19 ± 1.65 [−5.86, 3.07]	39.8	16.7
S‐I	2	N/A
	8	−0.02 ± 0.36 [−0.86, 0.70]	0.0	0.0	0.07 ± 0.69 [−1.78, 1.44]	14.5	0.49	0.24 ± 1.00 [−2.55, 2.05]	37.8	3.7
	10	−0.01 ± 0.51 [−1.13, 0.94]	3.8	0.0	0.11 ± 1.01 [−2.47, 1.96]	35.0	4.03	0.32 ± 1.36 [−3.34, 2.45]	53.3	16.7
	14	−0.02 ± 0.50 [−1.15, 0.92]	1.5	0.0	−0.07 ± 0.99 [−2.55, 1.77]	33.9	3.49	−0.24 ± 1.33 [−3.34, 2.33]	52.4	12.7

The GNL distortion magnitude in the LR direction tended to be more stable over time than in the AP and IS directions. Between the first and second timepoints, the LR and AP distortions showed <6% and 8% change, respectively, in the distortion magnitude over all of the radial ranges studied. However, ~10 months after initial commissioning, the MR‐linac multileaf collimators (MLCs) were replaced and as a result, the magnet was re‐shimmed (passive and cryoshim coils), yielding a detectable change in the GNL distortion particularly in the 20–25 cm range. In this range, the magnitude of distortions in the LR and AP directions were reduced by 15% and 18%, respectively, while in the IS direction was increased by 34%. Nevertheless, the results have remained stable with subsequent third and fourth timepoints, with IS distortions yielding the lowest variation (<3% change), followed by the AP distortions with <9% change across all ranges. While the AP distortions showed little variation in the 0‐10 cm range across the last two timepoints, they were reduced by 15% and 17% in the 10–20 cm and 20–25 cm ranges with the magnet reshim.

Fig. 3 shows results of routine measurements of the total MRI distortion spatial integrity with the phantom oriented along each axis over more than a year of clinical operation. Although these values represent the sum of distortions due to all sources, since GNL has been found to be the dominant source of distortion,²⁷ it can be considered the main contributor to these values. Notably, the scanner's spatial integrity within the first ~10 months of operation was stable (maximum variation around the mean value was 10% in the axial plane, 6% in the coronal plane, and 8% in the sagittal plane). During this period the maximum total distortion was 1.41, 0.99, and 1.56 mm in the Axial, Coronal, and Sagittal planes, respectively (results not shown). However, at month 11 when the MLCs were replaced and the magnet was re‐shimmed, a detectable change in the total spatial distortion of the MRI was also observed. This led to a reduction of the total distortion in the axial plane and an increase in the distortions in the coronal and sagittal planes, which was maintained in subsequent months. This same pattern can be observed in the detailed GNL measurements that were performed after the major repair, particularly in the SI direction where the percentage of landmarks >1 mm more than doubled at distances greater than 10 cm from isocenter (Table 1). The maximum total distortions over all observed timepoints were 1.41 mm (Week 0) in the axial plane, 1.56 mm (Week 27) in the sagittal plane, and 1.73 (Week 45) in the coronal plane (results not shown).

Figure 3.

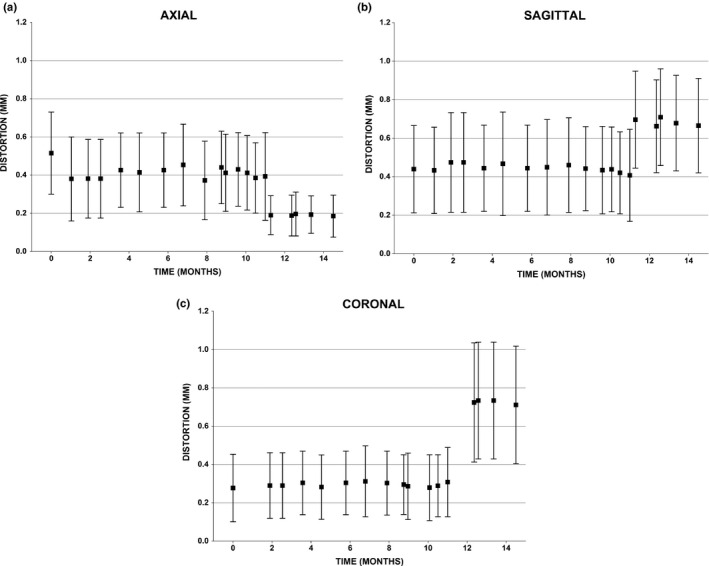
Temporal mean and standard deviations of the total distortions measured within the Axial, Coronal, and Sagittal planes using the spatial integrity phantom at different timepoints. At week ˜45, major MR‐linac repairs yielded a detectable change in the distortions as assessed by this routine quality assurance procedure.

4. Discussion

In this work, we characterized GNL and total distortions of a 0.35T MR‐linac over the course of 1 yr to assess the necessity of geometric distortion correction in MR‐IGRT applications, as well as to explore the temporal stability of geometric distortions. For measuring GNL distortions, we used an in‐house large FOV modular phantom²⁵ to isolate these distortions in the LR‐RL, AP‐PA, and SI‐IS directions. Our measurements in the MR‐linac resulted in outcomes similar to those measured by our group in other MR scanners. GNL distortion across three different MRI platforms was found to be <1 mm within 10 cm of magnet isocenter along all three axes,²⁵ which is comparable to the distortion measured in the 0.35T MR‐linac. Similarly, distortion along the LR and SI directions started to increase above 1 mm in all scanners as the radial distance from the isocenter increased; however, for the 1.5T and 3T scanners the AP distortions stayed almost within 1 mm. Similar to what has been observed in diagnostic and MR‐SIM scanners,²⁵ GNL‐based distortions in the MR‐linac increased in all three dimensions as the distance from the magnet isocenter increased. A notable observation in the distortion patterns as seen in Fig. 2 is the different behavior of GNL distortion in the z direction compared to distortion in the x and y directions. These plots show that compared to the x and y directions, a higher magnitude of distortion is seen in the z direction near the isocenter but lower magnitude at farther distances. These differences can be due to a different design of the z coil or a worse shim in the z direction as suggested by Torfeh et al. based on observing higher distortions in the z direction compared to the x and y directions on a 1.5T MR‐SIM unit.²¹

This study evaluated the GNL distortion based on a large FOV phantom and total distortion using a different, smaller FOV spatial integrity phantom. It is important to note that equivalence between the measures cannot be expected as the total distortion results represent a maximum distance from isocenter of <17.5 cm from a single plane oriented at isocenter, whereas the large modular FOV phantom is used to isolate contributions from GNL for each axis over >6,000 landmarks at a much greater radial distance (ie, a volume) from magnet isocenter. In a previous study on a 0.35T MR‐Co⁶⁰ using the same 2D spatial integrity phantom,³³ total distortion measurement over a larger FOV was accomplished by placing the phantom at different longitudinal distances from isocenter, yielding total distortions of up to 8 mm at 25 cm from isocenter. Extrapolating these results to this study, Table 1 shows that the GNL component of the total distortion along a single axis across all timepoints ranged from −7.3 mm to 5.39 mm for regions located 20–25 cm from magnet isocenter, which is similar in magnitude.

Previously, Hu et al. measured the total geometric distortions in the 0.35T field of a ⁶⁰Co MR‐IGRT unit using an American College of Radiology phantom using a balanced steady‐state free precision 3D sequence.³⁴ Their results showed maximum distortions of 1.5 and 2.7 mm within diameter spherical volumes of 20 and 35 cm (which is equivalent to the 10 and 17.5 cm radii in the current work). These measurements show a higher magnitude of distortion compared to our routine spatial distortion results, likely due to the phantom extending over a larger FOV. In a similar study, Ginn et al. characterized total spatial distortions in a 0.35T ⁶⁰Co MR‐IGRT unit using 2D and larger (465 × 350 × 168 mm³) 3D distortion phantoms.³³ The maximum distortion within 10 cm radius of isocenter was 1.15 mm using the 2D phantom. Based on their measurements, the maximum distortion within the 3D phantom was 8.13 mm, which is similar to the values obtained in our study. In both comparative studies, GNL was not isolated and total distortion was reported using the clinically released TrueFISP sequence. Furthermore, differences could also be attributed to the ⁶⁰Co MR‐IGRT unit only incorporating static passive shims placed into shim trays in the gradient coil along with cryoshim coils, whereas the MR‐linac design includes an additional rotational passive shim component within the bore.

The pattern of spatial distribution of the AP‐PA GNL distortions as displayed in Fig. 1 shows that while GNL distortions are generally worsened in the peripheral landmarks as the distance is increased from the isocenter, landmarks close to the central axis have small distortions, even up to 20 cm from the isocenter. A notable aspect of our study is repeated measurement of distortions over the course of 1 yr to assess spatial integrity of the scanner and temporal stability of distortions. Prior to a major equipment replacement, variations of distortion at different timepoints were relatively low (<10% for both GNL and total distortions along all axes and in all planes); however, after the change in the scanner hardware, considerable changes were observed in measured distortions. Although geometric distortions were still within the acceptable range, this highlights the necessity of distortion assessment after any hardware change in the scanner. Excluding the possibility of such changes and considering that GNL has been shown to be stable over time,³⁵ one benefit of isolating GNL is that distortion correction maps can be created to correct GNL distortions in MR images especially for situations where the anatomy of interest is not located near the magnet isocenter (ie, lateral treatments such as breast cancer³⁶).

One limitation of our study is the requirement of an MR/CT coregistration of the large FOV phantom. However, by performing a spatially constrained registration to the 15 × 15 × 15 cm³ volume around isocenter, distortions were not expected to contribute to the registration process, with no systematic offset observed near magnet isocenter as shown in Fig. 2. This was confirmed by measuring the displacement of the landmark located at the isocenter, with respect to its position on the CT image yielding displacements <0.2 mm for all axes, which is equivalent to a fraction of the acquisition voxel size. One other limitation of this work is that the analysis was based on discrete landmarks spaced 2.5 cm apart, yielding noncontinuous results shown in Fig. 2. However, given that >6000 landmarks were evaluated, the overall sampling across the large FOV was considered sufficient. To generate more continuous distortion maps of the full 3D space, methods such as singular value decomposition (SVD) can be used to interpolate the data by fitting it to polynomials.²⁶ Another limitation is that this work does not isolate the B0 inhomogeneity. However, early results have shown a dependence on gantry angle,^{35, 37, 38, 39} making it beyond the scope of the current work and worthy of a more detailed investigation. We should note that eddy currents generated by rapidly pulsed gradients may potentially influence image distortion,⁴⁰ which was not investigated in this work. However, when the impact of eddy currents on GNL results was acquired on a 1.0 T magnet over a range of TE values, the mean distortion in the transverse, coronal, and sagittal planes varied <0.2 mm over all TE settings.²⁶ Similarly, Baldwin et al. found negligible uncertainty (<0.3 mm) was introduced as a result of varying TE for a 3.0 T cylindrical magnet.²⁷ A comprehensive evaluation of different sequences, including T2‐weighted and spin echo sequences often used for pelvis and abdominal imaging, and the impact of eddy currents on GNL will be explored in future work. Finally, the results presented here are limited to the design and specific properties of the first 0.35T MR‐linac installation. Previously reported work in diagnostic MRI scanners has shown that GNL is magnet and platform specific,^{21, 25, 27} thus it is expected that each MRgRT device will have its own characteristics. Nevertheless, in the absence of major hardware changes, the GNL was found to be stable over time for this specific MR‐linac.

One potential concern regarding MR distortions is the effect it can have on dosimetric endpoints. Yan et al. studied the impact of MRI distortions on the dose delivered to the target and organs at risk in 14 patients.⁴¹ Based on their simulation and using vendor‐corrected MR images, they found that MR distortions can lead to <4% of the target volume coverage loss and potential increased doses to organs at risk of 5–6 Gy. In another recent study, Adjeiwaah et al. estimated <0.5% difference in the PTV dose in prostate cancer patients arising from residual system and patient induced susceptibility distortions.¹³ Data are still emerging to determine the acceptable magnitude of geometric distortions for MRgRT. More specifically, recommendations for GNL distortion accuracy are not currently well defined for MRgRT and are currently being addressed in AAPM TG‐284 for MR simulators and MRIs sited in Radiation Oncology. For most radiation therapy applications, an accuracy of 1 mm or higher is necessary.²⁷ In cases where the target size is smaller, geometric accuracy becomes a more critical issue, for example, for a target size of 3 cm, geometric distortions of 1.5 mm may impact the dose to 95% of the volume.¹⁵ According to a recent consensus paper from seven clinical institutes, in the case of MRI simulation for external beam radiation therapy, geometric distortion of <2 mm in the central region of treatment is deemed to be acceptable for sites such as brain, head and neck, and cervix.⁴² For real‐time MRgRT the desired precision has also been reported to be 2 mm.⁸

A clinical solution currently being implemented is to display iso‐distortion contours (typically 2 mm or 3 mm) to define the spatial accuracy of the image and alert the user to regions that have less geometric fidelity. If the distortion is found to exceed the expectations of the clinic, end users may work with their vendor colleagues to address the accuracy of the spherical harmonics solution and work to improve the distortion across a large FOV. Recent work by Tao et al. found that by using high‐order terms up to the 10th order, root mean square error could be reduced from 0.7 mm (5th order) down to 0.36 mm for a compact, asymmetric MR gradient system used for brain imaging.⁴³ This suggests that introducing additional terms into the solution may offer further potential to reduce GNL.

Potential clinical solutions include positioning the lesion closer to magnet isocenter by changing the patient setup or immobilization or incorporating the distortion uncertainty into the treatment planning margin. Based on our measurements, for cases where the anatomy of interest is within a range of 10 cm from the magnet isocenter, distortion can be considered to be negligible. However, our findings suggest that GNL distortions on the 0.35T MR‐linac may need to be accounted for when considering large FOV MR‐only planning on an MR‐linac or for instances when the anatomy is positioned away from magnet isocenter such as lateral lesions or targets that extend laterally or superiorly/inferiorly, such as with lymph nodes.

5. Conclusion

In the absence of hardware changes, GNL distortion was found to be reasonably stable for this particular MR‐linac. Measured GNL distortions were negligible within a 10 cm radius of isocenter in the L‐R, A‐P, and S‐I directions. However, in the periphery (>20 cm from isocenter), non‐negligible distortions up to ~7 mm were observed, which may necessitate GNL corrections for MR‐only planning, particularly in distant regions from the isocenter. Overall, when imaging is performed for larger anatomies or for MR‐only planning, distortion corrections might be necessary to support high precision radiation therapy for this specific MRgRT system.

Conflict of interest

The submitting institution has research agreements with ViewRay, Inc. but no financial support was received for the current work. Carri Glide‐Hurst discloses travel and honorarium from ViewRay, Inc. for speaking engagements and research agreements with Philips Healthcare.