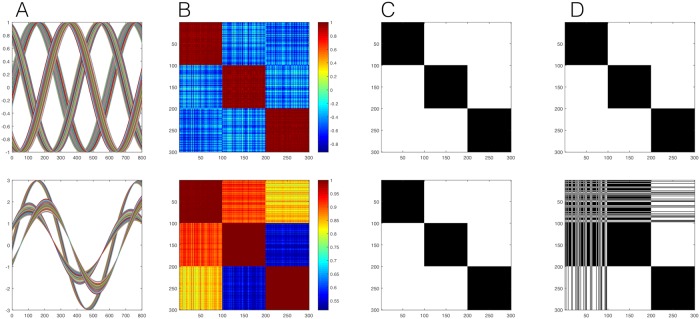
Fig 3. Illustration of misidentification due to the presence of common trends in a comparison between the method by Rubinov and Sporns [14] (based on a null model with independent entries of the correlation matrix) and our alternative approach (based on the more appropriate null model with dependent entries constructed from random matrix theory).

(A top) 300 synthetically generated time series in a system with 3 modules, each containing 100 oscillating series with random phases, (A bottom) 300 synthetically generated time series as before, with a strong global periodic signal. (B) the corresponding correlation matrix, top and bottom accordingly, showing a clear block structure. The output of our method (C) and the Rubinov-Sporns method (D) in terms of likelihood matrices indicating the frequency with which two neurons are found in the same community in 1000 runs of both methods. We can see that the Rubinov-Sporns method is able to correctly separates the 3 modules in the more straightforward case of clear positive and negative correlation (D top). In the more complex case where the correlation are obscured by a strong common trend the Rubinov-Sporns method merges the first module with the other two clusters. Using the proper null model our method is able to correctly separates the 3 modules in both cases (C).