Upstream vortex and elastic wave in the viscoelastic flow around a confined cylinder

Abstract

The viscoelastic flow past a cylinder is a classic benchmark problem that is not completely understood. Using novel 3D holographic particle velocimetry, we report three main discoveries of the elastic instability upstream of a single cylinder in viscoelastic channel flow. First, we observe that upstream vortices initiate at the corner between the cylinder and the wall and grow with increasing flow rate. Second, beyond a critical Weissenberg, the flow upstream becomes unsteady and switches between two bistable configurations, leading to symmetry breaking in the cylinder axis direction that is highly three-dimensional in nature. Lastly, we find that the disturbance of the elastic instability propagates relatively far upstream via an elastic wave, and is weakly correlated with that in the cylinder wake. The wave speed and the extent of the instability increase with Weissenberg number, indicating an absolute instability in viscoelastic fluids.

1. Introduction

The flow of a viscoelastic fluid past a cylinder is a benchmark problem in non-Newtonian fluid mechanics that is not completely understood (Ultman & Denn 1971; Dhahir & Walters 1989). Such flows are frequently encountered in technologies including filtration processes, flow in soil, and oil extraction (Chhabra et al. 2001) as well as porous biological systems, including blood flow pass cardiovascular valves (Marsden 2014) and brain tissues (Iliff 2012). In addition, the viscoelastic flow around cylinder arrays has been extensively used in the study of flow in porous media (De et al. 2017; Kawale et al. 2017) and instabilities at low Reynolds number (Varshney & Steinberg 2017; Qin & Arratia 2017; Haward et al. 2018). The viscoelastic flow past a single cylinder in an unbounded domain has been thoroughly investigated. In general, the curvature of the cylinder provides a perturbation to the fluid streamlines that can initiate viscoelastic instabilities above a critical condition (Pakdel & McKinley 1996). This behavior can be well captured by both linear instability analysis and numerical simulations (Ultman & Denn 1971; Mena & Caswell 1974; Chilcott & Rallison 1988), which show an increase in elastic stresses in the cylinder wake that can lead to velocity fluctuations and chaotic flow behavior. While the development of three-dimensional (3D) flow structures is an important stage in the onset of flow instabilities, particularly in wall-bounded flows (McKinley et al. 1993), such flow structures have yet to be experimentally characterized in detail.

Experimental investigations for unbounded and unidirectionally bounded cylinders have observed a wake instability downstream of the cylinder (McKinley et al. 1993) beyond a critical Weissenberg number, $Wi=\lambda \stackrel{.}{\gamma }$, where $\stackrel{.}{\gamma }$ is the shear rate and λ is the fluid relaxation time, as well as drag increase (James et al. 2016). Numerical simulations at moderate Wi found stress concentration in the cylinder wake (Alves et al. 2001) as well as transition to elastic turbulence (Grilli et al. 2013). Most of the existing literature on upstream instabilities, however, focus on contraction type geometries. The vortex development in axisymmetric or planar contractions has been investigated by many authors where the lip and corner vortices emerge, grow and become unsteady (Rodd et al. 2007; Lubansky et al. 2007; Miller & Cooper-White 2009; Rodd et al. 2010; Gulati et al. 2010; Hwang et al. 2017). The effects of contraction ratios are well studied and an array of polymeric solutions have been used, including long chain polymers, single DNA molecules, and surfactant systems. On the other hand, the development and characteristics of elastic instabilities upstream of an obstacle such as a cylinder have received far less attention. The cylinder differs from the planar constriction because the centerline of the upstream flow, where the velocity is maximum, reaches a stagnation point in the front of the cylinder, which results in strong extensional components in both the axis of the cylinder and the cross stream direction. In fact, recent investigations have shown a possible upstream instability (Shi & Christopher 2016) that can grow and even become unstable; the coupling of upstream instabilities and downstream wakes has been hypothesized to drive this complex flow, which can be highly three dimensional, as shown by numerical studies (Omowunmi & Yuan 2010). Despite recent efforts, the dynamical transition and the 3D flow structure of this upstream instability has not been fully resolved experimentally.

Using 3D particle tracking methods, we report three main discoveries of the elastic instability upstream of a single cylinder in confined channel flow. First, we report the onset of upstream instability in the form of 3D corner vortices in front of the cylinder (where the cylinder intersects the wall) whose size grows with increasing flow rate. Second, beyond a critical flow rate, the vortex becomes unsteady and switches between two bistable configurations that lead to symmetry breaking in the cylinder axis direction and is highly 3-dimensional in nature. Surprisingly, the disturbance of the elastic instability propagates far upstream in the form of an elastic wave, yet remains relatively isolated from the flow in the cylinder wake. The elastic wave speed is found to increase with increasing Wi.

2. Experimental methods

The flow of a dilute polymeric solution is investigated using a straight microchannel made from polydimethylsiloxane with a rectangular cross section with width W = 100 μm and height H = 60 μm. A single cylinder with diameter d = 50 μm is located far (300 W) from the inlet and is centered in the channel width direction. The device schematic is shown in figure 1 (a). Fluid flow is driven at constant flow rate using syringe pump.

Figure 1.

(a) Schematic of the experimental setup. (b-c) Snapshots of the streak plots showing the unsteady vortex upstream of the cylinder.

The polymeric solution is made by mixing 300 μg/g of polyacrylamide (Polyscience, 18×10⁶ MW) in 90 wt% glycerol aqueous mixture. Rheology measurements can be found in (Qin & Arratia 2017). The polymeric solution has a nearly constant viscosity of η = 0.3 Pa·s, close to solvent viscosity of 0.23 Pa·s for the shear rates used here. The Weissenberg number is defined from the strength of elastic stress to viscous stress as $Wi(\stackrel{.}{\gamma })=N_1(\stackrel{.}{\gamma })∕2\stackrel{.}{\gamma }\eta (\stackrel{.}{\gamma })$ where the characteristic shear rate is defined by the mean centerline velocity, ${\overline{U}}_c$, $\stackrel{.}{\gamma }={\overline{U}}_c∕H$ and N₁ is the first normal stress difference. The fluid is seeded with 1 μm polystyrene tracers at 0.01 vol%.

We visualize the channel using both traditional particle streak velocimetry and novel in-line holographic 3D tracking. For the holographic tracking, the seeded flow is illuminated by a laser (635 nm) mounted on an inverted microscope and recorded using a high speed camera, details in (Salipante et al. 2017). The positions of the particles are determined using back-scattering reconstruction and 3D velocity fields are obtained by differentiating Lagrangian particle trajectories.

3. Results

3.1. Upstream vortex: growth and fluctuation

We begin our analysis by investigating the flow structures upstream the cylinder. Figure 1(b,c) shows two snapshots of streaks taken at z = 10 μm (from bottom plane) of the channel for Wi = 23. These two-dimensional streak plots illustrate the highly unsteady vortices immediately upstream of the cylinder. We observe the presence of a large recirculation region in front of the cylinder which clearly separates the dominant bulk flow into two streams. To quantify the onset of the upstream vortex, we monitor its length χ normalized by the cylinder diameter d as a function of Weissenberg number at a particular height (z = 10 μm). The length is defined as furthest upstream point with zero or negative velocity to the edge of the cylinder. This stagnant vortex extends far upstream with maximum normalized vortex length of about χ/d ≈ 6 as in figure 1(b). The feature of the vortex is marked by flow recirculation with relatively low or negative velocity compared to the bulk flow. At higher Wi, the vortex is highly unsteady and frequently collapses (figure 1c) and regenerates in time.

In figure 2(a), we plot the mean vortex length (black dots) for all sample observations (80 snapshots over a duration of 200 s) as a function of Wi; the vortex length χ is normalized by cylinder diameter d. We note that for the Newtonian solvent, no vortex or irregular flow is observed at all flow rates. For the viscoelastic fluid, however, we can clearly identify four regimes as a function of Wi. For Wi ≲ 2 (regime I in figure 2a), the flow around the cylinder possesses fore-aft symmetry identical to the creeping flow shown in figure 2(b). For Wi ≳ 2, however, we see the emergence of a recirculation zone comprised of two rotating vortex rolls that are symmetric relative to the line y = 0 passing the center of the cylinder, as in figure 2(c). The flow is steady and the pattern does not change over several minutes. As Wi is further increased, the stagnant region becomes highly elongated and extends further upstream along the centerline (regime II in figure 2a), before reaching another flow transition at Wi ≈ 4. For Wi ≳ 4 (regime III in figure 2a), the extent of the recirculation zone becomes unsteady and fluctuates weakly in time. This can be seen in the 5^th and 95^th percentile of all observed vortex lengths, shown by the shaded area in figure 2(a). These percentile curves begin to deviate from the mean in this regime, indicating variation in the sampled vortex lengths. The unsteadiness of the vortex length is also reflected in the increase of root-mean-square(rms) fluctuation of χ/d, shown in figure 2(a) inset. The rms fluctuation, however, saturates before reaching Wi ≈ 9. In this regime (III), the vortex varies significantly in size with Wi and the lateral symmetry of the two vortex rolls is lost, as shown in figure 2(d). Lastly, for Wi ≳ 9, the flow enters into a regime where the vortex frequently collapses suddenly to a length of approximately 2d and then regenerates, as shown by the constant 5^th percentile curve despite increasing Wi. The vortex length frequently “pulse” in time with large rms fluctuations, as shown previously by the streak plots in figure 1(b-c). The mean vortex length continues to grow with Wi and extends far upstream, reaching 6d (3W) at Wi = 16.

Figure 2.

(a) Normalized vortex length χ/d (see text) as a function of Wi. Black dots represent the mean of vortex length sampled over 200 s and open triangles represent the maximum vortex length measured using holographic microscopy. The shaded region is bounded by 5^th and 95^th percentiles. Four regimes of vortex dynamics can be identified. I: steady Stokesian flow with fore-aft symmetry. II: emergence of steady vortex in front of the cylinder. III: onset of weak time-dependence. IV: pulsing vortex which collapses and regenerates. Inset: rms fluctuation of χ/d. (b) Streak plot for regime I. (c) Streak plot showing vortex symmetry around channel centerline at Wi≈4 and (d) subsequent symmetry breaking at Wi ≈ 8 in regime III.

The origin of the vortex regions may be understood in terms of minimization of the flow extension due to high fluid extensional viscosity, similar to other contraction geometries (Boger 1987; Rodd et al. 2007). In such geometries, the flow field develops recirculating vortices in order to produce an effectively longer entrance region for the flow to increase in velocity gradually, which reduces the extension rate $\stackrel{.}{ϵ}\sim \partial U∕\partial x$ around the cylinder.

We note that in the high Trouton ratio limit (high extension), the length of a vortex extending upstream from the lip of a planar contraction has been predicted to increase linearly with Wi and is independent of Trouton ratio (Lubansky et al. 2007). We find similar behavior here in that the (normalized) vortex length increase linearly with Wi (figure 2a) although quantitative comparison is not applicable between the two geometries.

Although the observed vortex is measured in an x – y plane, the structure and dynamics are far from two-dimensional. In fact, the structure of the flow switches from two bistable modes in the z direction, as we explore next.

3.2. Upstream vortex: 3-d structures

In order to visualize the full flow structure upstream of the cylinder, we use holographic particle tracking to reconstruct the three-dimensional flow field. To identify the stagnant region, characterized by negative stream-wise velocity, we plot the iso-surface where the velocity magnitude is zero. Figure 3(a,b) shows two snapshots of the spatial structure of the stagnant region at different times. It is clear that the flow is in fact made up of a pair of two separate recirculation zones originating near the corner of the cylinder with the walls. The vortex regions extend upstream along the top and bottom surfaces. Moreover, the vortex growth along one wall is accompanied by the suppression of the vortex on the other wall, which is confined to the space immediately in front of the cylinder. The switching between the two states occurs irregularly in time: as the stagnant zone collapses on one side, the other vortex reforms.

Figure 3.

Three dimensional structure of the stagnant vortex upstream of the cylinder in the pulsing regime (Wi = 23). (a) Snapshot of the stagnant vortex defined by the iso-surface for zero speed U = 0, showing the dominance of the vortex near the top wall. (b) The complementary case where the vortex near the bottom wall dominates. (c,d) Velocity map along a cross-section passing through the channel centerline for similar cases shown in (a,b).

The flow symmetry breaking in the z-direction is evident in figure 3(c,d), where the corresponding velocity field in a x – z cross-section along the channel centerline is plotted. The presence of the adverse flow (blue) clearly alters the surrounding bulk flow, as shown by the streamwise flow (red) in figure 3(c,d). The generation of adverse flow originates along the upstream side of the cylinder that drives flow along top or bottom surface. In the pulsing regime, the extended vortex region can separate from the cylinder and move upstream along the top or bottom surface. Meanwhile, the other vortex expands in the z-direction and fills the space directly in front of the cylinder.

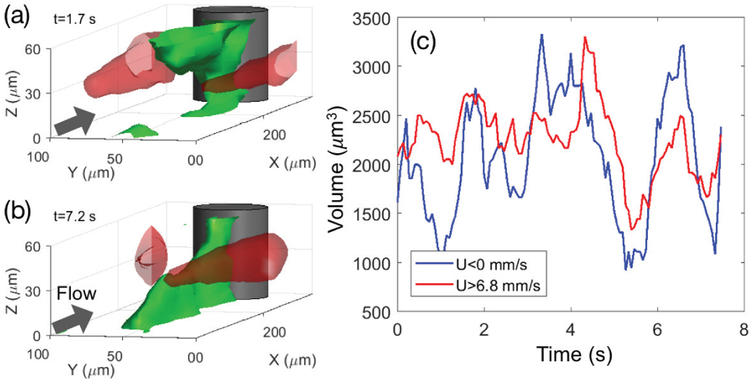
In figure 4(a,b), we distinguish the bulk flow from the vortex region by comparing the high-velocity iso-surface U = 6.9 mm/s with the low-velocity ones U = 0 mm/s, measured simultaneously. We find that when the extended stagnant vortices are present, the bulk flow separates into two high velocity regions surrounding the stagnant region. Similarly, periods of weakened vortex development correspond to transitional states where the bulk flow occupies larger cross-section at a lower velocity. In figure 4(c), we compare the volume of the stagnant vortex (low velocity region) and the bulk flow (high-velocity region) within 1W upstream of the cylinder, which shows that the two signals are indeed highly correlated.

Figure 4.

(a,b) Surfaces of equal velocity in front of the cylinder at two different time instances. Regions of zero x-velocity form in front of the cylinder along the top or bottom walls. High velocity regions (U = 6.9 mm/s isosurface) separate along the left and right sides of the channel. (c) The volume of the high speed flow region (U ⩾ 6.9 mm/s) compared to the volume of the back flow U ⩽ 0 over a length of 1W upstream of the cylinder. The strong correlation indicates that vortex region acts to constrict the bulk flow into a smaller region.

The flow symmetry also breaks down in the span-wise y-direction, resulting in a shift of the primary flow to either the left or right of the channel. For instance, figure 4(a) shows the region has shifted the predominant flow towards the left side and figure 4(b) shows the dominant flow on the right. This results in a greater flow along the right side of the cylinder. In fact, the flow rate around either side of the cylinder are found to be anti-correlated due to the constant volume flow rate, but can vary by approximately 20 % from the mean, suggesting flow switching and symmetry-breaking in the span-wise y direction. These lateral symmetry breaking and fluctuations may be intimately linked to the onset of finite flow perturbation observed in (Pan et al. 2013) and (Qin & Arratia 2017).

Lastly, although the variation in flow to either side of the cylinder may produce further flow fluctuation downstream, the flow instability associated with the vortex formation is only weakly communicated downstream. In fact, we find that the flow disturbance actually propagates far upstream.

3.3. Disturbance propagation and elastic waves

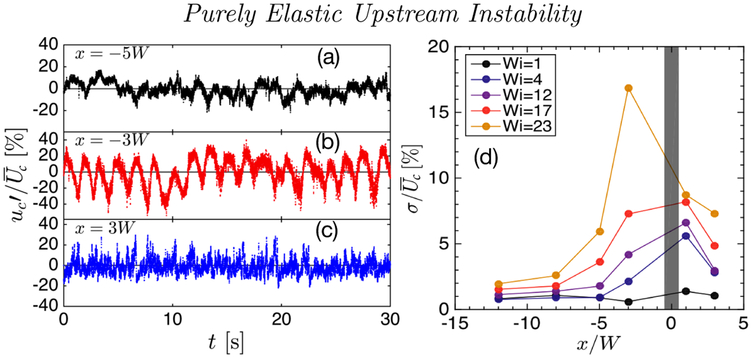
The unsteady vortex is accompanied by bulk flow instabilities far upstream. To quantify the fluctuation in the unstable flow, we conduct particle tracking velocimetry focused on a small window in the channel centerline (z = 30 μm) and monitor the instantaneous stream-wise velocity u_c at various channel x locations. The fluctuation is then obtained by subtracting the mean from the instantaneous velocity, $u_c^{\prime }=u_c-{\overline{u}}_c$. To facilitate comparison between various flow rates, we normalize the velocity fluctuation with the mean centerline velocity ${\overline{U}}_c$ far from the cylinder. In figure 5(a,b), we plot the time series of the normalized velocity fluctuations at −5W and −3W upstream of the cylinder. We observe large fluctuations (20 % of the mean flow) for the viscoelastic flow compared to the Newtonian solvent (gray line). The flow downstream of the cylinder at comparable location, however, sees a different type of fluctuation. The amplitude of the fluctuation is smaller and the signal shows frequent jumps to the high velocity amidst dwelling at low velocities. This suggests two different instabilities up and downstream of the cylinder.

Figure 5.

(a) Fluctuation of the centerline velocity $u_c^{\prime }$ normalized by the mean far from the cylinder at an upstream location x = −5W for Wi = 23, where upstream vortices are pulsing, (b) at x = −3W and (c) downstream at x = 3W. The gray line represent the flow of the Newtonian fluid at similar flow rates in each of these plots. (d) The normalized root mean square of the centerline velocity fluctuation at various channel locations and Weissenberg number.

The impact of the vortex instability is not confined to the vicinity of the cylinder but propagates upstream. In figure 5(d), we plot the root mean square velocity fluctuation σ normalized by ${\overline{U}}_c$ at various x locations. For low Weissenberg number (Wi ≲ 1), we see very little velocity fluctuations at all channel locations. As Wi increases, we see that the flow downstream of the cylinder becomes unstable, as expected from the well-known wake instability. The flow upstream, however, also saw a significant increase in velocity fluctuations. As Wi further increases, the upstream velocity fluctuation rapidly grows in strength and propagates increasingly further upstream. At Wi = 23, it can be felt over 10W upstream of the cylinder and the largest fluctuation magnitude is in front of the cylinder at −3W. Very far upstream (20W above), the flow is found to be steady with fluctuations close to the instrument noise.

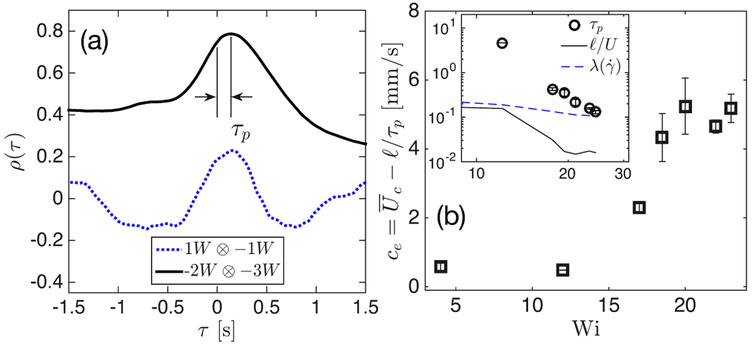
The propagation of upstream disturbances suggests a mechanism for transmitting perturbations against the primary flow direction, even in the presence of strong advection. Specifically, we investigate the relay of disturbances by computing the two-point crosscorrelation between the two observation points separated by a distance ℓ. In figure 6(a), we compute the cross-correlation coefficient for two streamwise velocity magnitudes measured simultaneously at −3W and −2W upstream of the cylinder. First, we see that the two signals are highly correlated, with a maximum ρ(τ) reaching almost 0.8. Note that a perfect correlation has ρ = 1, anti-correlation has −1, while uncorrelated signal has ρ = 0. However, the peak shift time τ_p is around 0.14 s, which indicates that the velocity signal at −3W leads −2W by 0.14 s. This lead time turns out to be much longer than the advection timescale, $\ell ∕{\overline{U}}_c$, which is around 0.018 s.

Figure 6.

(a) Cross-correlation between pairs of stream-wise velocity signals measured simultaneously at different locations for Wi = 23. The pairwise locations are indicated by the legend, (b) The elastic wave speed computed via the peak shift time as a function of Wi, obtained from the pair −2W ⨂ −W, where the disturbance is strongest. Inset: lag time and various time scales to compute the elastic wave. Error bars represent uncertainty estimated from statistical bootstrapping using time series sub-intervals.

The propagation of the disturbance due to the elastic instability has a smaller effect on the flow in the cylinder wake. When we compare the velocity signal measured simultaneously 1W upstream and downstream of the cylinder and we find that the signals are weakly correlated compared to those upstream. Although notably, the peak shift time is similar to the correlations made at two points upstream of the cylinder. This weaker correlation is expected from the very different velocity time series shown in figure 5(b,c), where the characteristics of the fluctuations are markedly different. Although some of the flow fluctuations are communicated downstream of the cylinder due to finite relaxation time, the instability mechanisms of the flow upstream and downstream the cylinder are clearly distinct, one relies on the propagation of elastic wave while the later on the elastic hoop stresses.

The increase in peak shift time occurs if there is a wave traveling upstream with wave speed, c_e that goes against the bulk advection in the lab frame. The net result is a reduction in speed and increase in the time needed to travel, ${\tau }_p=\ell ∕({\overline{U}}_c-c_e)$. We note that the minus sign implies the wave is going in the direction opposite to the bulk flow and the shift time reflects the competition between the wave speed going upstream and the advection of fluid downstream. All quantities other than c_e can be directly measured, we can then compute c_e. Since the flow is steady without fluctuation below Wi = 4, we only report results for Wi ≳ 4. Additionally, accuracy of the method relies on a large velocity fluctuation from which a shift time can be measured. We therefore focus on positions with large fluctuations and note that only the flow in the pulsing regime has a clear wave speed. The peak shift times are measured to extract the corresponding wave speed for between two locations −2W⨂−W, shown in figure 6(b) for various Weissenberg number.

As shown in figure 6(b), the elastic wave speed increases with Weissenberg number for Wi ≳ 10, rather than a constant value. This implies that as Wi increases, the disturbance increases in strength and propagates upstream faster. A comparison of the measured mean advection time, $l∕{\overline{U}}_c$, and peak shift times (inset of figure 6(b)) show that both timescales decrease in a similar power law relationship with Wi. This is in contrast to the fluid relaxation time $\lambda (\stackrel{.}{\gamma })$, which decreases only slightly over this range of Wi, showing that the wave speed doesn’t simply scale with polymer relaxation time. An increase in the wave speed upstream of the cylinder with Wi gives an indication of an absolute instability, rather than one that is convected with the flow (Van Saarloos 2003; Monkewitz 1988). Nevertheless, the finite extent of the upstream perturbations suggests there is a mechanism for dissipation or slow down of the elastic wave.

4. Conclusion

Using holographic particle tracking methods, we study the structure and dynamics of the flow of viscoelastic fluids around a confined cylinder. In contrast to most previous studies, we observe the formation of a stagnant flow region in front of the cylinder. We attribute the difference to the confinement of the microchannel, which produces a strong extensional flow component similar to a planar constriction where entrance vortices are observed. However, the flow around a cylinder differs from contraction type flows since the cylinder separates the flow into two separate streams. The stagnant vortex regions form along the top and bottom of the channel at a critical Wi number. As flow rate increases, the streamwise length of the vortex increase linearly with Wi, similar to theory for entrance flows of high Trouton ratio fluids.

The velocity fluctuations of the viscoelastic fluid in front of the cylinder are 3-dimensional in nature, notably shifting upward and downward (in the axial direction of the cylinder) around the stagnant regions which extend along the top and bottom walls. Additionally, the flow separation around the cylinder results in a breakdown in the left-right flow symmetry, which biases the bulk flow to one side of the cylinder over the other. At sufficiently high Wi, the flow becomes temporally unstable and undergoes rapid switching between dominant states and produces a violent pulsing behavior. The strong symmetry breaking in the both the channel height and width direction results from the confined cylinder geometry, which provides more varied flow fields compared to a planar contraction.

Strikingly, the disturbance propagates beyond the extent of the vortex. We observe that the flow downstream of the cylinder also becomes unstable, although the strength of the instability upstream is considerable stronger at high Wi. Although separated only by a cylinder 50 μm in diameter, the flow fields before and after the post appear to be fairly isolated from each other and possess very distinct temporal and spatial features. The cross-correlation between the flow at two positions before the post clearly shows the propagation of an elastic wave, which provides a mechanism by which perturbations can travel upstream. The elastic wave is found to increase in speed and penetrate farther upstream with Wi, indicating an absolute instability emanating from the cylinder. Our results provide insight into the mechanisms by which perturbations travel in viscoelastic fluids and build towards understanding the more complex flows such as in porous media.