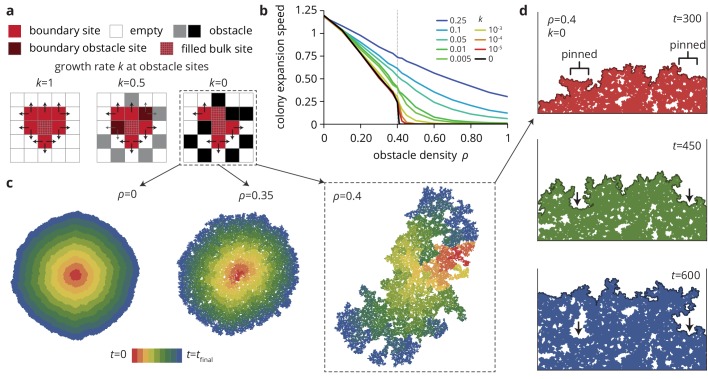
Figure 4. A minimal model captures the change in colony morphology in heterogeneous environments.

(a) The simulation proceeds by allowing cells with empty neighbors ('boundary sites’) to divide into empty space. Disorder sites (gray/black, density $\rho$) are randomly distributed over the lattice. (b) As the obstacle transparency, that is the growth rate $k$ at disorder sites, is reduced, the colony expansion speed decreases as a function of the obstacle density. For impassable disorder sites ('obstacles’, $k=0$), the expansion speed vanishes above a critical obstacle density ${\rho }_c\approx 0.4$, beyond which the population was trapped and could not grow to full size. (c) As $\rho$ approached ${\rho }_c$ colony morphology became increasing fractal. Colors from red to blue show the colony shape at different times. (d) Near the critical obstacle density ${\rho }_c\approx 0.4$, only few individual sites near the front have empty neighbors, leading to local pinning of the front (arrows), where the front can only progress by lateral growth into the pinned region.

Figure 4—figure supplement 1. Characterization of Eden clusters with obstacles ($k=0$).

(a) Taking the front speed $v$ as the order parameter, there is a phase transition at a critical obstacle density ${\rho }_c(L)$ depending on system size $L$. For an infinite system, ${\rho }_c\approx 0.41\pm 0.01$. For $\rho <{\rho }_c$, we have $v\sim {|\rho -{\rho }_c|}^{0.21}$. (b) Roughness $W$ of fully developed interfaces at $L=400$ for varying obstacle densities, as a function of the window length $l$, such that $W\sim t^{\alpha }$. At $\rho =0$, we find $\alpha =1/2$, consistent with the KPZ universality class. At ${\rho }_c$, we find ${\alpha }_{\mathrm{loc}}\approx 0.9$, consistent with the QEW universality class (see Theory in the Materials and methods section), which is known to be characterized by two roughness exponents, a local exponent (${\alpha }_{\mathrm{loc}}$, panel b), and a global exponent ${\alpha }_G\approx 1.15>{\alpha }_{\mathrm{loc}}$ when the roughness is measured over the whole system size (see panel c) (Amaral et al., 1995). Importantly for $0<\rho <{\rho }_c$, there is a crossover length scale below which the system displays QEW scaling, whereas it returns to the KPZ scaling on longer length scales. (d) The time evolution $W(t)\sim t^{\beta }$ of the interface also follows dynamics consistent with KPZ ($\beta =1/3$) and QEW ($\beta \approx 0.78$) in the limiting cases. For intermediate $0\ll \rho \ll {\rho }_c$, there is a crossover from qEW at short times to KPZ dynamics at longer times, before the roughness saturates at a $\rho$-dependent value. For easier analysis, all simulations were performed in a box-like geometry.