Semi-quantification and grading of amyloid PET: A project of the European Alzheimer's Disease Consortium (EADC)

Abstract

Background

amyloid-PET reading has been classically implemented as a binary assessment, although the clinical experience has shown that the number of borderline cases is non negligible not only in epidemiological studies of asymptomatic subjects but also in naturalistic groups of symptomatic patients attending memory clinics. In this work we develop a model to compare and integrate visual reading with two independent semi-quantification methods in order to obtain a tracer-independent multi-parametric evaluation.

Methods

We retrospectively enrolled three cohorts of cognitively impaired patients submitted to ¹⁸F-florbetaben (53 subjects), ¹⁸F-flutemetamol (62 subjects), ¹⁸F-florbetapir (60 subjects) PET/CT respectively, in 6 European centres belonging to the EADC. The 175 scans were visually classified as positive/negative following approved criteria and further classified with a 5-step grading as negative, mild negative, borderline, mild positive, positive by 5 independent readers, blind to clinical data. Scan quality was also visually assessed and recorded. Semi-quantification was based on two quantifiers: the standardized uptake value (SUVr) and the ELBA method. We used a sigmoid model to relate the grading with the quantifiers.

We measured the readers accord and inconsistencies in the visual assessment as well as the relationship between discrepancies on the grading and semi-quantifications.

Conclusion

It is possible to construct a map between different tracers and different quantification methods without resorting to ad-hoc acquired cases. We used a 5-level visual scale which, together with a mathematical model, delivered cut-offs and transition regions on tracers that are (largely) independent from the population. All fluorinated tracers appeared to have the same contrast and discrimination ability with respect to the negative-to-positive grading. We validated the integration of both visual reading and different quantifiers in a more robust framework thus bridging the gap between a binary and a user-independent continuous scale.

Highlights

• •Scans acquired with all commercial amyloid-PET fluorinated tracers are compared.
• •2 independent semi-quantification methods provided whole-brain amyloid load values.
• •5 readers independently evaluated all scans using a graded scale.
• •A mathematical model is used to link visual grading to semi-quantification.
• •Mapping between tracers and reader evaluation are given.

1. Introduction

Assessment of brain Aβ amyloidosis has gained a pivotal role in the diagnosis of Alzheimer's disease (AD) in vivo, according to the last National Institute of Aging-Alzheimer Association (NIA-AA) (McKhann et al., 2011, Albert et al., 2011) and the International Working Group-2 (IWG-2) criteria (Dubois et al., 2014). Moreover, the 2018 research framework identifies a stage of Alzheimer pathology for isolated brain amyloidosis while the term AD is reserved to the concomitant amyloid and tau pathology (Jack Jr et al., 2018). The concordance between CSF Aβ42 levels and amyloid load on PET is good (over 80%; Hansson et al., 2018) although data shows that CSF Aβ levels changes may precede brain amyloid deposition and thus it should be considered as an earlier phenomenon (Palmqvist, 2016). Instead, brain amyloid load on PET still continues to increase even after the onset of cognitive symptoms (Farrell et al., 2017). Moreover, the availability of Aβ40 assays has shown that a non-trivial part of patients are high or low Aβ amyloid producers so that the Aβ42/40 ratio better reflects the real amyloidosis status of a subject and allows better correlation with amyloid load on PET (Niemantsverdriet et al., 2017).

The amyloid PET reading has been classically implemented as a binary lecture, i.e., negative or positive for amyloidosis, however the current clinical experience has shown that the number of borderline cases is not trivial not only in epidemiological studies in asymptomatic subjects but also in naturalistic groups of symptomatic patients attending a memory clinic to receive a diagnosis (Payoux et al., 2015). This behaviour actually mirrors what happens with CSF Aβ assay showing a non-negligible borderzone around the cut-off value identifying positive and negative subjects (Molinuevo et al., 2014).

The APOE genotype (presence of at least one epsilon-4 allele) is a major determinant of the degree of amyloidosis (Drzezga et al., 2009) but other, less known factors may play a role (Wang et al., 2017). In any case, the binary lecture is poorly adequate to address the clinical reality and complexity and, even within the two extreme classes – i.e. negative or positive – there is inhomogeneity because there are subjects that are more or less positive and those who are more or less negative (Fleisher et al., 2011). Taking together all this information, brain amyloidosis across subjects attending a memory clinics appears more as a continuum rather than a clusterized, binomial distribution.

Therefore, the issue arises on how to quantify and grade such a continuum, whether the continuum with a specific fluorinated radiopharmaceutical is similar to the one obtained with the other two available fluorinated radiopharmaceuticals, and how to share this information among labs. The so-called “centiloid project” (Klunk et al., 2015) has tried to give an answer to this issue and is certainly of value but it requires that each center builds-up its own cohort of normal subjects in different age ranges. Moreover, it is based on SUVr computation that certainly has advantages but also disadvantages, such as the uncertainty about the reference region and on how to draw the cortical ROIs.

In the present study and in the frame of the PET study group of the European Alzheimer's disease Consortium (EADC) we aim at: (a) propose and validate a method to compare semi-quantification values among tracers regardless of the semi-quantification approach (SUVr-based or SUVr-independent); (b) define transition regions and cut-off values which are (largely) independent from the cohorts; (c) test a more complex visual evaluation scale common across different tracers and assess its performance.

2. Methods

2.1. Subject selection

The amyloid PET project of the EADC (PET 2.0 [1]) is aimed at joining together amyloid PET scans with corresponding clinical and neuropsychological data from subjects attending a memory clinic of one of the EADC centers.

To the purpose of this project, both subjects with a positive or negative amyloid PET scan according to visual dichotomic evaluation, as established by the local nuclear medicine physician, were enrolled.

We identified the fluorinated tracer with the lowest number of scans available (i.e., ¹⁸F-florbetaben, 53 subjects) and then a similar number of subjects with the other two fluorinated tracers (¹⁸F-flutemetamol, 62 subjects; ¹⁸F-florbetapir, 60 subjects). Only with the ¹⁸F-florbetapir we randomly sampled the database in order to maintain the highest possible number of centers overlapping with the other two tracers, and to maintain an approximate balance in number of cases per center. These subjects constitute three cohorts, one per each tracer. The selection was done from some of those EADC centers participating to the PET 2.0 project, namely: Genoa (GEN), Brescia (BRE), Geneva (HUG), Antwerp (ANT), Paris (PAR), and Mannheim (MAN) according to scan availability on the tracer of choice. Subjects main demographics and clinical characteristics are summarized in Table 1.

Table 1.

Demographics.

	F-18 flutemetamol			F-18 florbetaben			F-18 florbetapir
Provenance	GEN	PAR	HUG	GEN	MAN	HUG	GEN	BRE	ANT	HUG
Sample size	15	33	14	15	30	8	15	15	6	24
Scanner	Siemens BioGraph HiRes 1080	GE Discovery 690	Siemens Biograph 128 mCT	Siemens BioGraph HiRes 1080	Siemens BioGraph 40 mCT	Siemens BioGraph 128 mCT	Siemens BioGraph HiRes 1080	Siemens BioGraph 40 mCT	Siemens BioGraph 64 mCT	Siemens BioGraph 128 mCT
Age [y]	69.7	62.3	60.3	72.6	66.2	69.2	72.5	72.0	77.5	71.0
	[54 79]	[42 78]	[45 70]	[55 82]	[48 84]	[51 71]]	[59 80]	[60 84]	[68 85]	[59 83]
Sex (M %)	46.7	40.0	49.1	60.0	56.7	30.0	51.9	45.0	16.7	45.8
MMSE score	26.7	27.9	28.2	27.7	24.6	27.1	26.1	22.1	25.1	27.6
	[18 30]	[24 30]	[25 30]	[24 30]	[14 30]	[2030]	[15 30]	[13 28]	[15 30]	[1330]
MCIAD (%)	24.1			41.5			23.1
possAD (%)	1.6						3.4
probAD (%)	4.8			18.8			15.0
probFTD (%)	1.6			3.8			3.2
possFTD (%)	4.8						3.4
possDLB (%)	1.6
probVaD (%)							1.5
PseudoDD (%)	1.6			13.2			10.0
aMCI (%)	14.6			3.8			8.2
naMCI (%)	32.2			9.4			6.5
SCI (%)	13.0			9.4			25.7

Subjects received a diagnosis after the first diagnostic work-up, including the result of amyloid PET scan, and were followed-up clinically for an average time of 30.1 [6–143] months. We considered the diagnosis as clinically confirmed at the last available visit. The selected subjects were diagnosed as affected by mild cognitive impairment (MCI) due to AD (MCIAD), probable (prob) or possible (poss) AD dementia, frontotemporal dementia (FTD), dementia with Lewy bodies (DLB), or vascular dementia (VaD) according to current criteria (McKhann et al., 2011; Albert et al., 2011; Rascovsky et al., 2011; McKeith et al., 2005; Gorelick et al., 2011). Moreover, those subjects who did not received a definite pathogenetic diagnosis were still labeled as affected by amnestic (aMCI) or non-amnestic (naMCI) MCI. The population also included some subjects with the so called ‘pseudodementia’ (pseudoDD, that is, psychiatric conditions that can mimic dementia), or with subjective cognitive complaints but without evidence of deficit on neuropsychological tests (SCI).

The study was approved by the local Ethics Committees and all the recruited subjects provided an informed consent.

2.2. PET acquisition

Amyloid PET acquisition followed the recommendations of tracer manufacturers and the joint guidelines of the European Association of Nuclear Medicine and the Society of Nuclear Medicine (Minoshima et al., 2016). The equipment used was a PET-CT tomograph and is listed in Table 1 for each center. Three-dimensional static scan acquisition was performed in all centers, and attenuation correction was based on CT. Image reconstruction was made with Ordered Subset-Expectation Maximization algorithm following the standard brain protocols embedded in each equipment. Each center was responsible for sending good-quality data but a further quality check was performed by the core center in Genoa. In order to reproduce the clinical situation in the real world, only unreadable scans were rejected while all other scans were submitted to further analysis.

2.3. CT subset

A subset of all cohorts – 50% in total: 39 subjects with flutemetamol, 29 with florbetaben and 20 with florbetapir – came with the companion CT scans. While all PET scans were read without CT, the subset with the CT underwent a separate, further evaluation following the same rules detailed in Visual Evaluation. The intent is to use this subset to validate the statistics of evaluation and accord among readers even when the assessment was conducted without the CT.

2.4. Visual evaluation

The 175 scans were independently presented to five readers, including three expert (UPG, FN and VG) and two intermediate-expert readers (AC and MB). The three experts passed the training qualification of the three vendors and are used to report several scans monthly since the time of availability on the market of the radiopharmaceuticals, always with the agreement of at least another expert and with the assistance of semi-quantification based on both SUVr and SUVr-independent tools (Chincarini et al., 2016). The two intermediate-expert readers share the same characteristics as the experts but are reading scans for a shorter time.

The anonymized scans were presented in the native space, randomized, and the reader was blind to the clinical information and the reading of the other experts. No MRI or CT scans were provided together with PET scans (see also CT subset comparison).

Readers were asked three questions as follows:

• A.quality flag: a dichotomous response on sub-optimal scans. There is no formal or shared definition on scan quality. This flag was raised according to each reader own's experience. Typically though sub-optimal quality involves image acquisition flaws like field of view cuts or poor count rate; it can also be related to image reconstruction issues like excess smooth, artefacts, etc.
• B.binary evaluation: negative/positive according to the approved indications of each manufacturer.
• C.5-step evaluation: visual grading into classes: {negative, mild negative, borderline, mild positive, positive} according to Paghera et al., 2019 (see below).

Readers were presented with 3 batches (flutemetamol, florbetaben, florbetapir) and they were informed of the tracers used.

The evaluation of each batch was completed sequentially, with at least 2 weeks time between one batch and the next. After the three evaluation batches, the CT subset was sent to the readers to get a new independent evaluation with the help of the companion CT.

2.5. Semi-quantification methods

The visual assessment of the amyloid PET scan is a non-trivial task that is often complemented by measures derived from semi-quantification methods (hereafter named quantifiers). These measures are intended to be proxies of the brain amyloid load.

Among quantifiers, the Standardized Uptake Value ratio (SUVr) (Kinahan and Fletcher, 2010) is the most widely used and validated, compared to the binary reading.

This approach calculates the ratio of PET counts between a target region of interest (ROI) versus a reference one. In this study the SUVr was estimated using the whole cerebellum as reference region. As reported in the literature (Schmidt 2015), this choice makes the measure less prone to segmentation errors than the selection of the cerebellum gray matter or the brain stem. The SUVr score was calculated as the average cortico-cerebellar SUVr on all scans. Similarly to what accomplished in (Klunk et al., 2015), the target cortical ROI included the medial frontal gyrus, the lateral frontal cortex (middle frontal gyrus), the lateral temporal cortex (middle temporal gyrus), the lateral parietal cortex (inferior parietal lobule), the insula, the caudate nucleus, and the precuneus-posterior cingulate region.

The other quantifier used in this study is named ELBA (Chincarini et al., 2016). It is a SUVr-independent approach that is designed to capture intensity distribution patterns rather than actual counts in predefined ROIs. These patterns are global properties of the whole brain and do not require a reference ROI. ELBA showed good performance versus the visual classification, highly significant correlation with the result of CSF Aβ42 assay, and has ranking characteristics proven both on cross-sectional and longitudinal analyses (Chincarini et al., 2016).

Similarly to the procedure described in (Chincarini et al., 2016), quantifiers were applied onto the spatially-normalized image. Briefly, the procedure mapped the PET onto the T1-weighted MRI template in MNI space (with isotropic spacing and voxel dimension of 1x1x1 mm) with a registration consististing in: global intensity re-scaling, rigid registration, affine registration. Then, a pre-segmented atlas which included cortical and cerebellar ROIs was mapped from the MNI space to the affine-transformed PET with a deformable registration. We used the ANTs registration software (Avants et al., 2011) with the mutual information metric.

Both quantifiers were implemented in an automatic analysis procedure that did not require any human supervision with the exception of an visual check after the spatial normalization process onto the MNI space.

2.6. Analysis

2.6.1. Sample homogeneity and data model

Direct comparison of semi-quantification values over different tracers is possible in principle, if one is in possess of a set of subjects who have been acquired with two or more tracers over a reasonably short time frame (i.e. with respect to the typical physiological change in amyloid deposition). Alternatively, one could use statistically equivalent reference cohorts. This latter approach is the one followed by the centiloid method, where the ad-hoc acquisition of a group of young healthy controls and a group of confirmed AD subjects – both analyzed with the quantification method of choice – constitutes the centiloid scale references.

Unfortunately our three cohorts are not statistically equivalent (both in sample size, center distribution and clinical evaluation) and neither can they be considered scale extremes, so that direct comparison among semi-quantification values cannot be applied.

Given that the visual reading is the de-facto gold standard in assessing positivity in a clinical setting, we can exploit it as cross-tracer comparison method. A model is therefore necessary to link the visual assessment to the semi-quantification. The binary reading is though too coarse to provide a meaningful relationship, we therefore resort to the grading.

Positivity grades have been conventionally declined into numbers ranging from 1 to 5 (negative → mild negative → borderline → mild positive → positive). Basic considerations on the transition continuity and on the floor/ceiling effect on negative/ positive evaluations suggest that a possible model of the grading versus semi-quantification is a sigmoid function (S), which we write in the following form:

$$g=p-\frac{p-n}{1+exp\left[-s\left(q-o\right)\right]}=S\left(q,s,o\right)$$

where ‘g’ is the grading, ‘p’ and ‘n’ are the numerical equivalent of the positive and negative gradings, ‘q’ is the quantification value, ‘s’ is the slope and ‘o’ is the offset.

For each tracer, the sigmoid function of our model has only 2 free parameters: the slope ‘s’ and the offset ‘o’. All other parameters are set by the limit grading values (negative for quant. score → -∞, positive for quant. score → ∞). This ensures that the models are (largely) independent from the sample characteristics because of the few degrees of freedom versus the sample size (~60 scan in each cohort).

Models are used in synergy with visual grading to provide a mapping between tracers.

2.6.2. Readers concordance

Readers evaluated all scans independently. We can therefore assume that their errors are uncorrelated and that their mean is a good estimator of the “true” evaluation. While this holds true for a large number of measures, we need to ensure that the error on the mean is relatively small even when employing 5 readers only. This assumption is acceptable if the accord among readers is sufficiently high.

To assess reader concordance we compute the intra-class correlation coefficient (ICC, two way random-effect model, mean of k raters) for the whole dataset and on the single cohorts (one per tracer, Table 3). Between each reader we also compute the Cohen k.

Table 3.

ICC Two way random-effect model, mean of k raters (absolute agreement).

Tracer	ICC [95% CL]
Flutemetamol	0.952 [0.93 0.969]
Florbetaben	0.987 [0.98 0.992]
Florbetapir	0.959 [0.94 0.974]
All tracers	0.967 [0.96 0.975]

For each tracer and for each reader we compute the grades statistics, i.e. the number scans in each grade (Table 2).

Table 2.

Evaluation fraction by grade.

	Reader	negative (%)	mild neg (%)	borderline (%)	mild pos (%)	positive (%)
All tracers	UPG	23	14	5	22	36
	FN	25	10	9	17	39
	AC	17	18	21	19	26
	VG	11	22	9	19	38
	MB	22	21	10	14	33
	All	19.6	17	10.8	18.2	34.4
Flutemetamol	UPG	15	23	8	32	23
	FN	23	10	15	19	34
	AC	8	16	35	18	23
	VG	6	24	13	24	32
	MB	23	26	11	18	23
	All	15	19.8	16.4	22.2	27
florbetaben	UPG	25	9	2	13	51
	FN	23	13	2	11	51
	AC	21	11	6	17	45
	VG	19	15	4	17	45
	MB	23	15	8	13	42
	All	22.2	12.6	4.4	14.2	46.8
florbetapir	UPG	30	10	5	18	37
	FN	30	7	8	20	35
	AC	22	25	18	23	12
	VG	10	27	8	17	38
	MB	20	22	10	12	37
	All	22.4	18.2	9.8	18	31.8

The between tracer distribution is also visually shown with a heatmap (number of scans per each grade pairs) and the Bland-Altmann plot (Fig. 7 in Supplementary materials).

2.6.3. Visual assessment and semi-quantification

The relationship between visual grading and quantification is found by fitting the sigmoid model onto the data. Model parameters are fit both onto z-score quantifier values (direct model, grading vs. quantifiers) and on the raw quantifiers data (inverse model, quantifiers vs. grading).

In the direct model, each scan is identified by the z-scored value of the quantifier (either ELBA or SUVr) and by its average grading. z-scores are computed on each cohort separately.

With the z-scores model we can easily visualize relationships with the two quantifiers on the same plot and we can evaluate potential significant differences, both between quantifiers and among tracers.

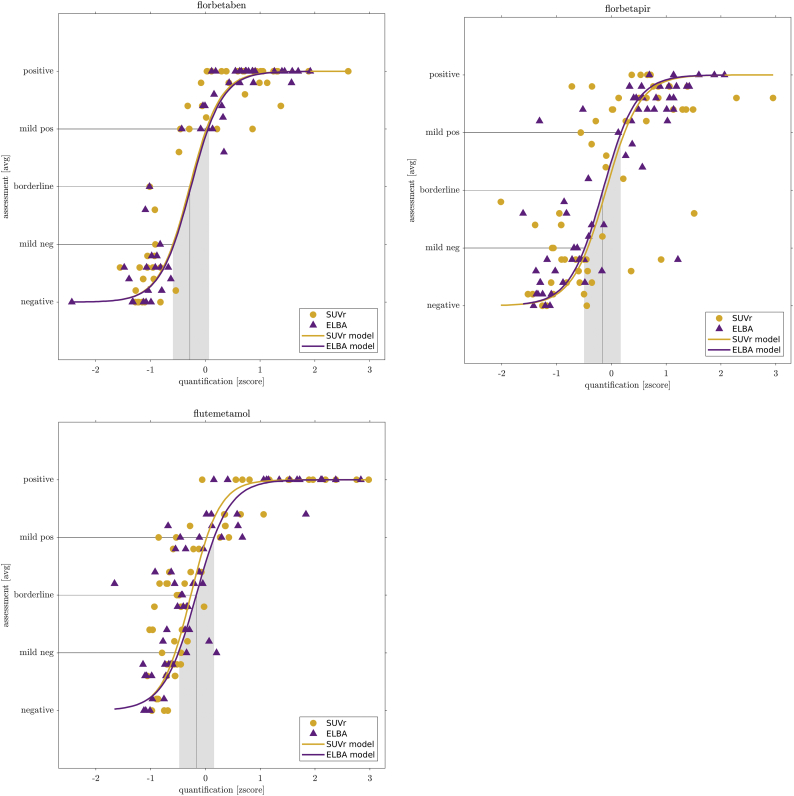
We use the fitted models to define a transition region (from mild-negative to mild-positive) and the cut-off on all tracers. These quantities are found at the intersection of the models with the mild-negative, borderline and mild-positive coordinates on the y-axis (Fig. 1).

Fig. 1.

Quantification-visual assessment relationship for the 3 fluorinated tracers. On the x-axis: z-score of the two quantifiers; on the y-axis the average visual grading. Dots represents scans, continuous line is the sigmoid model. Intersection of model with mild and borderline evaluations is projected onto the scores to define a transition region (gray area) and the cutoff (gray line).

Both the transition region and the cut-off values depend on the data only through the model, so they can be considered a proxy of cohort-independent definitions.

Given their good correlation (see Fig. 3), the two z-scored quantifiers can be further summarized into a single value, that is the score on the first PCA axis (PCA₁). This allows us to abstract the quantification (potentially including more than two quantifiers) and focus on the relationship with the gradings.

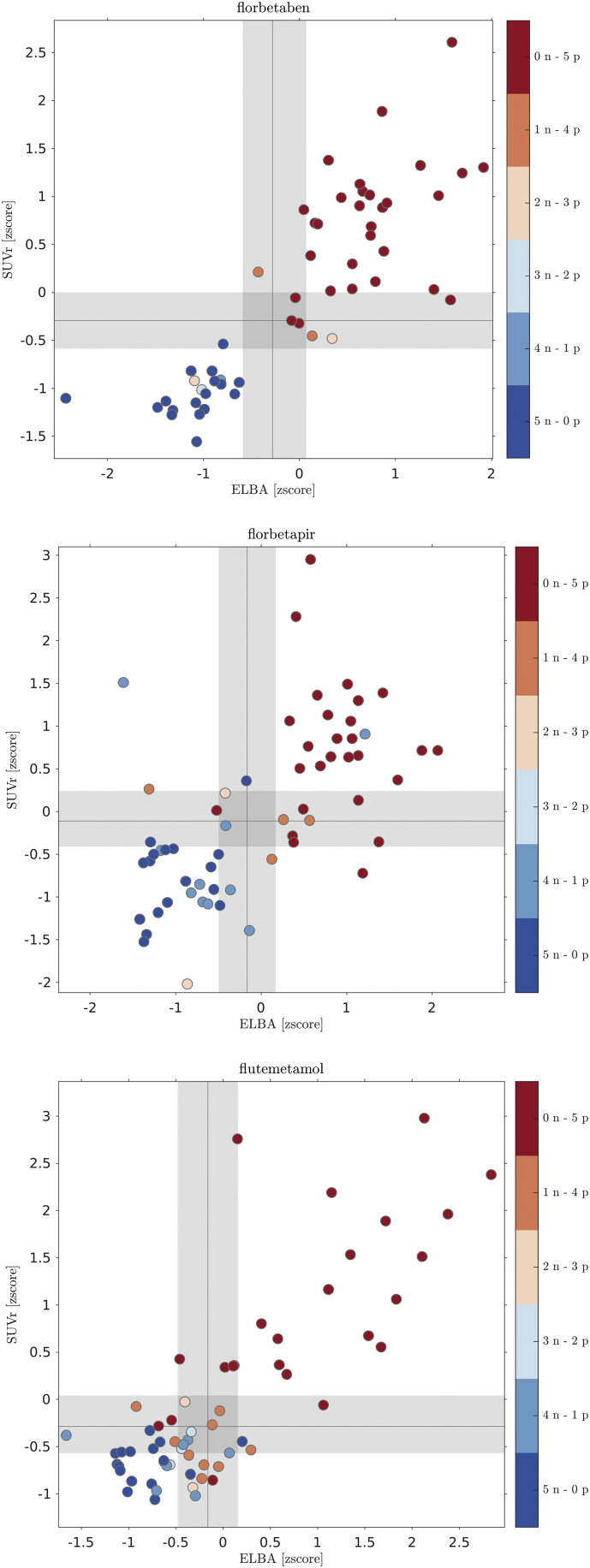
Fig. 3.

ELBA-SUVr scatter-plot with binary visual assessment. Dots represent scans, colors are according to the combination of negative and positive evaluations given by the 5 readers.

While the direct model is useful for comparison and visualization, the inverse model is used to estimate the between-tracers mapping.

2.6.4. Evaluation latitude

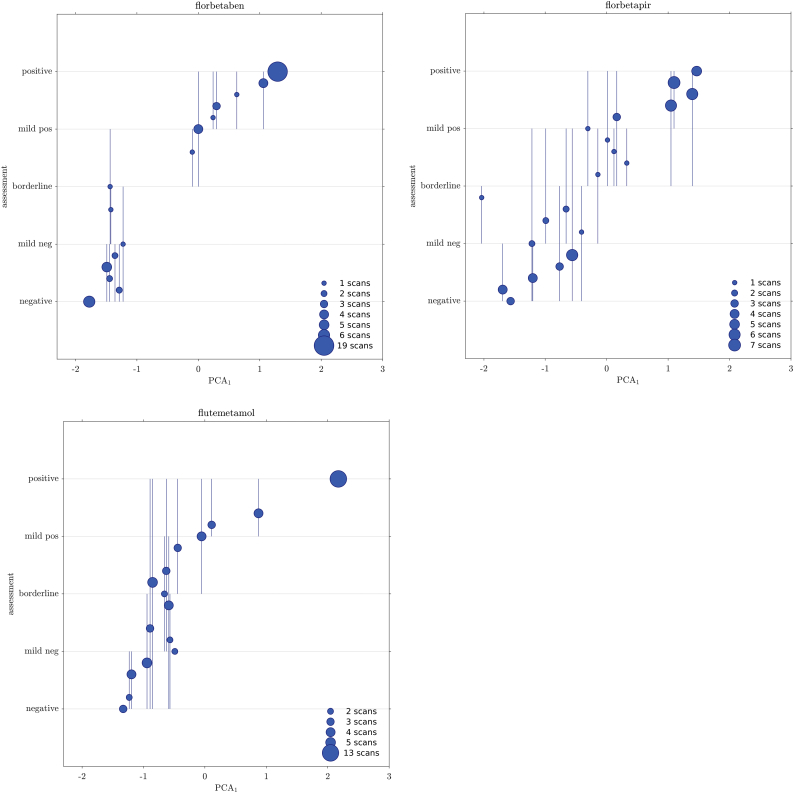
We grouped scans according to similar average grading. Groups may contain one or more scans. Each group is assigned a quantification value, which is the average score of its members onto the PCA₁.

Each group is also assigned an “evaluation latitude”; with this term we intend the overall scope of gradings, that is, the largest span of evaluations given by all readers on a scan or group of scans. The group evaluation latitude is therefore a range, spanning the lowest to highest grading received on any of the group's member.

The relationship between group's score and latitude provides further information on the reading discrepancies as function of the quantification (Fig. 2).

Fig. 2.

Relationship between quantification score and evaluation latitude. Each circle represents a group of scans sharing the same average grading. The group position on the x-axis is the average score of its members on the first PCA axis (PCA computed on the z-score quantifiers). The group position in the y-axis is the average grading. Vertical lines show the group evaluation latitude, that is, the lowest to highest grading received on any of the group's member.

2.6.5. Binary assessment

Each reader assigned a binary visual assessment – negative (n)/positive (p) – to the scan, according to each tracer's standard evaluation rules. With 5 independent readers we have therefore 6 possible classes: 5n-0p, 4n-1p … 0n-5p. We explored the distribution of the binary reading on a scatter-plot which also shows the relationship between the quantifiers.

We used the cut-off and the transition regions derived from the model (section Visual assessment and semi-quantification) to compute accuracies for both quantifiers. In this latter analysis we considered negative scans as belonging to classes {5n-0p, 4n-1p, 3n-2p} and positive scans as belonging to classes {2n-3p, 1n-4p, 0n-5p} (Fig. 3).

The reader accord on the binary assessment is shown with the Cohen k, to be compared to the grading (Tables 4 and 7).

Table 4.

Agreement between pairs of readers all tracers with respect to the grading evaluation using accuracy and Cohen k (within brackets).

	UPG	FN	AC	VG	MB
UPG		0.61 (0.48)	0.55 (0.44)	0.59 (0.46)	0.61 (0.49)
FN	0.61 (0.48)		0.60 (0.49)	0.62 (0.49)	0.62 (0.50)
AC	0.55 (0.44)	0.60 (0.49)		0.58 (0.46)	0.55 (0.43)
VG	0.59 (0.46)	0.62 (0.49)	0.58 (0.46)		0.53 (0.39)
MB	0.61 (0.49)	0.62 (0.50)	0.55 (0.43)	0.53 (0.39)

Table 7.

Agreement between pairs of readers on all tracers with respect to the binary evaluation using accuracy and Cohen k (within brackets).

	UPG	FN	AC	VG	MB
UPG		0.90 (0.80)	0.91 (0.81)	0.89 (0.76)	0.86 (0.71)
FN	0.90 (0.80)		0.91 (0.82)	0.93 (0.84)	0.86 (0.72)
AC	0.91 (0.81)	0.91 (0.82)		0.90 (0.79)	0.86 (0.71)
VG	0.89 (0.76)	0.93 (0.84)	0.90 (0.79)		0.87 (0.74)
MB	0.86 (0.71)	0.86 (0.72)	0.86 (0.71)	0.87 (0.74)

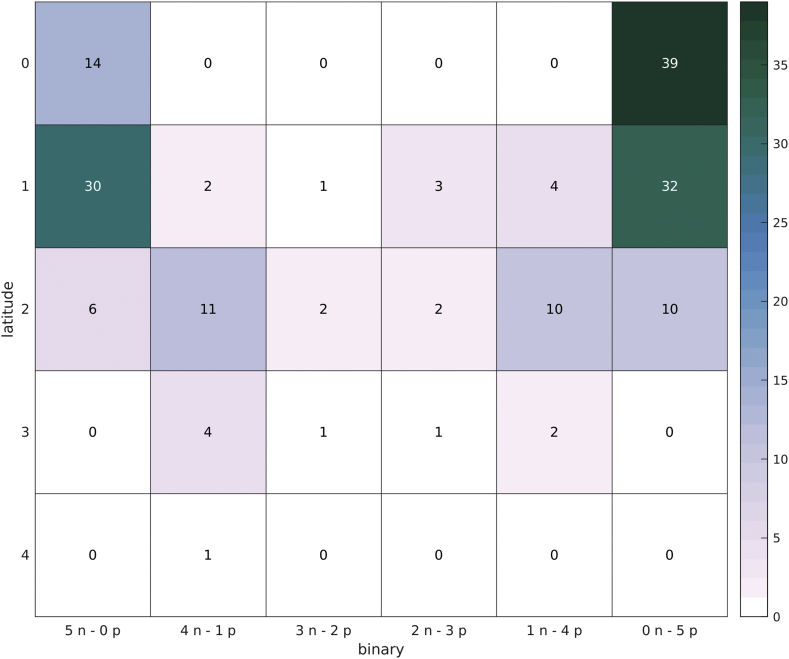
Then, we looked at possible relationships between the binary reading and the discrepancies on the grading (latitude). For each scan we assigned the binary class (among the 6 possible choices) and we computed the latitude, i.e. the maximum grading difference among those received. We then counted how many scans are there per class and latitude (Fig. 4).

Fig. 4.

Relationship between the binary evaluation and the latitude. Each box shows the number of scans grouped by binary class and maximum grading difference received in the 5-step visual assessment.

2.6.6. Scan quality effect

The third type of visual assessment is the scan quality. This is simply a flag indicating whether acquisition nuisance and/or reconstruction procedures would result in a sub-optimal image, according to each reader's own experience.

We study whether scan quality has any relationship with quantification and evaluation latitude.

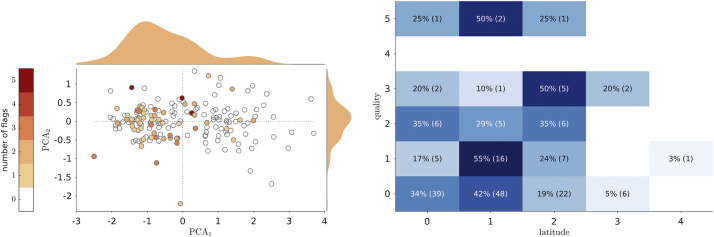
First we plot the number of quality flag versus the second PCA components (PCA₂). The PCA₁ encodes the quantification (negative to positive), while the PCA₂ mainly encodes discrepancies between the quantifiers (approximately off-diagonal distances in the ELBA-SUVr scatter plots, Fig. 3). We then look at biases in the quality distribution.

Then, we compute the matrix of the number of quality flags for each scan grouped by the latitude (i.e. the grading range).

2.6.7. CT subset comparison

Finally we compare evaluations on the subset with companion CT. Comparison between evaluations with/without CT is carried out by testing χ² statistics on the 5-step grading and binary distribution, and by comparing the intra-rater ICC and Cohen's k.

2.6.8. Mapping

We have now all the tools to map quantifications on one tracer into another. While the direct model ‘S' maps z-scored quantifier values into gradings, the inverse model ‘S⁻¹′ maps the gradings into the raw quantification values. If we keep the visual gradings as constants across tracers, we can bind two models together (model mapping).

Mathematically, this means that for each tracer pair ‘i-j’ we have a set of two equations for the inverse model S⁻¹, with model parameters s (slope) and o (offset, see Table 6):

$$q_i=S^{-1}\left(g,s_i,o_i\right)$$

$$q_j=S^{-1}\left(g,s_j,o_j\right)$$

Table 6.

Model parameters.

Tracer	Quantifier	Slope	Offset
Raw values (inverse model, quantifier vs. grading)
Flutemetamol	SUVr	−10.05 [−10.84 –9.26]	1.11 [1.04 1.18]
	ELBA	−13.41 [−14.54 –12.28]	0.76 [0.72 0.79]
Florbetaben	SUVr	−7.71 [−8.01 −7.41]	1.23 [1.17 1.29]
	ELBA	−9.65 [−10.06 –9.24]	0.85 [0.82 0.89]
Florbetapir	SUVr	−16.97 [−18.70 –15.24]	1.16 [1.11 1.21]
	ELBA	−11.40 [−12.00 –10.80]	0.87 [0.84 0.90]
z-score values (direct model, grading vs. quantifier)
Flutemetamol	SUVr	3.80 [2.91 4.70]	−0.27 [−0.53 −0.00]
	ELBA	3.37 [2.57 4.17]	−0.17 [−0.51 0.17]
Florbetaben	SUVr	3.60 [3.01 4.19]	−0.29 [−0.54 −0.03]
	ELBA	3.54 [3.01 4.07]	−0.26 [−0.50 −0.02]
Florbetapir	SUVr	3.27 [2.39 4.15]	−0.10 [−0.40 0.21]
	ELBA	3.32 [2.79 3.84]	−0.16 [−0.40 0.09]

These represent the expected (i.e. modeled) quantifier value q of the i-th and j-th tracer calculated in the grading coordinate g. As g ranges in [1..5], we therefore have a vector of 5 quantifier coordinates [q_i, q_j]. These coordinates are linearly regressed to find the mapping functions listed in Table 9.

Table 9.

conversion parameters between tracers (model mapping).

From/to	Flutemetamol	Florbetaben	Florbetapir
ELBA
Flutemetamol		1.39 x – 0.20	1.18 x – 0.02
Florbetaben	0.72 x + 0.15		0.85 x + 0.15
Florbetapir	0.85 x + 0.02	1.18 x – 0.17
SUVr
Flutemetamol		1.30 x – 0.22	0.59 x + 0.51
Florbetaben	0.77 x + 0.17		0.45 x + 0.61
Florbetapir	1.69 x − 0.86	2.20 x – 1.33

Another possible and distinct approach is to consider visual grading ranges as containers, in order to group subjects into comparable sets; that is, we might consider as equivalent two sets from different tracer cohorts, whose subjects received a mean average grading between – say – negative and mild negative. Container classes would therefore be 4: negative to mild negative, mild negative to borderline, borderline to mild positive, mild positive to positive. This latter approach is similar to the centiloid one, as it aims at constructing a series of comparable groups across tracers cohorts, thus avoiding the need for a model. In principle, albeit with a much higher number of scans, we could detect deviations of the mapping from a linear dependence, a possibility that is lacking in the centiloid method.

The linear regression over container cohorts is done on the average quantifier values and takes into account standard deviations on both quantifiers according to York et al., 2004.

While we are plagued by the relatively small number of subjects in some of the intermediate container classes, we still use this approach to cross-check the model mapping. We therefore require that the model mapping be compatible with the (linear) regression computed on container classes.

2.6.9. Validation

Last analysis is a validation of the mapping model. We run a MonteCarlo simulation to construct populations sharing the same grading distribution. For instance, we first select a reference cohort A – say the florbetaben scans – and another test cohort B – say the flutemetamol scans. The visual grading distributions of cohorts A and B are typically statistically different (Kolmogorov-Smirnov test p-value <.05). We now resample cohort B with appropriate weights (and with repetition), in order to create a new cohort B′ whose grading distribution is statistically equivalent to the cohort A.

If we look at the distribution of quantification values of the two cohorts A and B′ (either with ELBA or with SUVr) we still find these distributions statistically different because of the different tracers (i.e. quantifiers values are expressed in their own tracer units). We show that when we apply the model mapping we can nullify the statistical differences between A and B′.

In essence, population resampling plus model mapping give statistically equivalent results as if we had a single population that underwent multiple-tracers acquisitions.

3. Results

3.1. Readers concordance

The statistics on the grading evaluations is summarized in Table 2. The general overall assessment of accord among readers on the grading is measured by the ICC (two way random-effect model, mean of k raters, absolute agreement, Table 3). The agreement is very good (>95%) both on the whole dataset and on the single cohorts. ICC on Florbetaben is higher due to the relative lack of borderline cases in the graded evaluation (higher rate of AD-like diagnosis, Table 1).

The Cohen k for agreement between pairs of reviewers ranged from 0.39 to 0.49 (fair agreement, Table 4).Overall, the borderline scans were 10.8% (a non-trivial amount) whereas in the 35.2% of cases the readers defined the scan ‘mildly’ positive or negative.

A more detailed comparison among raters is shown in Fig. 7 (supplementary materials): this plot summarizes statistics and between readers agreement grouped by the 5 gradings. The heatmap representation – where color intensity is proportional to the number of scans – shows where discrepancies are more likely to occur. Besides the transition region, which is an obvious candidate, severe deviations from the diagonal (i.e. Δ grade > 2) can occur on all grades, albeit on very few scans.

Finally, we show the number of discrepancies grouped by severity in Table 5.

Table 5.

number of scans with minor (Δ grade ± 1), mild (Δ grade ± 2) and severe discrepancies (Δ grade > 2).

tracer	no discrepancy	minor	mild	severe
flutemetamol	19	21	16	6
florbetaben	26	22	5	0
florbetapir	8	29	20	3
all tracers	53	72	41	9

3.2. Visual assessment and semi-quantification

The model-mediated relationship between the grading and the quantifiers is shown in Fig. 1. There is no significant difference among models (z-score), both with respect to quantifiers and with respect to tracers (direct model, Table 6).

The transition region width is very similar among tracers, showing that there is no substantial difference in assessing the negative/positive contrast both with different tracers and with different quantifiers. For instance, the ELBA transition region width (in z-score units) is 0.64, 0.66 and 0.67 for flutemetamol, florbetaben and florbetapir respectively. These numbers are all compatible when we consider the parameters uncertainty.

3.3. Evaluation latitude

We now group subjects by average evaluation and we plot them versus their mean quantification value (here the score on the PCA₁). We can graphically represent the group's latitude by means of a line that spans the lowest and highest evaluation received by any member of the group (Fig. 2). We can glance at the latitude distribution and see that it tends to cluster in the mild negative to borderline region.

3.4. Binary assessment

Reader agreement is ranked according to Cohen k (Table 7) and values ranges from 0.71 to 0.84 (substantial agreement). Accuracies based on binary semi-quantification (i.e. above/below cutoff) are reported in Table 8.

Table 8.

Quantifiers accuracies.

Tracer	SUVr	ELBA
Flutemetamol	0.85	0.80
Florbetaben	0.92	0.96
Florbetapir	0.85	0.90
Weighted average	0.87	0.89

The distribution of the binary reading is shown on the quantifier scatter-plot in Fig. 3. We see that pure classes {5n-0p, 0n-5p} nicely cluster in the lower-left and upper right quadrant respectively, whereas intermediate classes (particularly {2n-3p, 3n-2p}) tend to aggregate near both transition regions.

Gray areas and gray lines are the transition regions and cut-off values derived from the intersection of the models with the mild-negative / borderline / mild-positive coordinates.

3.5. Scan quality effect

The distribution of quality flags is shown on all tracers together versus the two PCA components computed on the quantifiers (Fig. 5 left). There is a marked bias toward negative-to-borderline scans while there seems to be no relation with respect to quantifiers discrepancy (PCA₂ axis).

Fig. 5.

Left: distribution of the quality flags in the PCA plane; dots represents all scans, color is proportional to the number of quality issues raised by the 5 readers; marginal distribution shows the kernel density estimation. Right: heatmap of quality and latitude, showing the fraction of scans normalized on the quality and the actual number of scans sharing the same quality interpretation and evaluation latitude (within brackets).

Comparing quality to latitude, one would expect a positive trend linking the number of quality flags and the assessment discrepancies. Results shows that the latitude is substantially independent on the quality, hinting to a solid performance and coping ability of the trained eye (Fig. 5 right).

3.6. CT subset

We compute the intra-rater statistics on the assessments with and without the CT (88 scans, ~50% of the whole dataset).

χ² statistics was calculated on all tracers and for each reader on both the grading and the binary frequencies. No significant difference was found on the grading (for all readers, χ² < 4.72, p-value >.35) and on the binary evaluation (χ² < 0.75, p-value >.38).

The ICC on the grading, for all raters and on the whole CT dataset, is 0.982 [0.980–0.987].

The Cohen's k, computed on the grading and per rater, is: k = 0.65, 0.84, 0.76, 0.78, 0.85 for UPG, FN, AC, VG, and MB respectively.

We conclude therefore that there is no significant difference in the evaluation statistics when the CT is present.

3.7. Mapping and validation

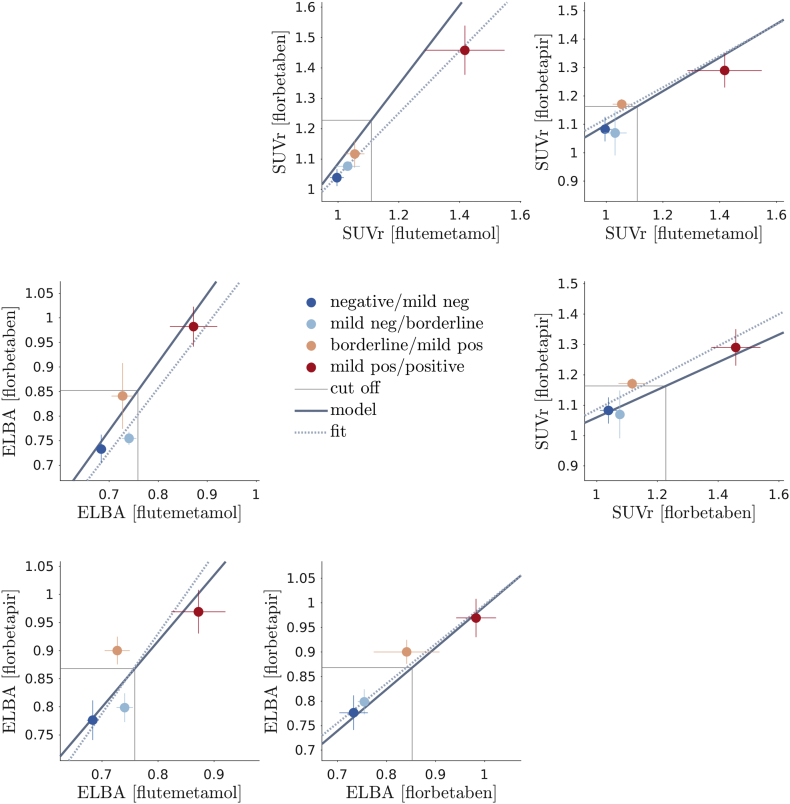
The complete set mapping functions between one tracer to another is shown in Fig. 6.

Fig. 6.

Matrix plot of all between-tracers models and container-cohort fits. Dots represent the average quantification on the cohort containers, lines crossing the dots are the standard deviations. The thick line is the model mapping, the dashed thin line is the linear regression based on the average quantification values (container mapping). Cut-offs are based on the model mapping.

The mapping function looks linear because of the substantial equivalence between model parameters (see Table 6). We can then easily convert any value from one tracer's own units into another (in particular the cut-off and the transition region), as detailed in Table 9.

Similarly we can use cohort containers (i.e. grouping subjects by average visual assessment lying between two adjacent gradings) to fit a linear regression. The cohort container regression does not require the sigmoid model and relies on the visual assessment only modestly, as we are fitting the average container values. Results show that the model fitting is well within the container regression error (see Table 10 in the supplementary materials).

4. Discussion

We have shown that it is possible to construct a map between different tracers and different quantification methods without resorting to ad-hoc acquired cases, as required in the centiloid approach or in studies where the same subjects are injected with more tracers.

In doing this we, used a 5-level visual scale, to define cut-offs and transition regions on tracers in a way largely independent from the population.

The link between the graded visual scale and semi-quantification is the sigmoid model. The use of the sigmoid function simply derives from the considerations that the amyloid load is a biologically continuous process with two boundaries (i.e. saturation at both the decidedly negative and positive range), which naturally translates in a smooth (i.e. infinitely derivable) function with finite limits and a near-linear response in the transition.

Obviously, other functional models could do, and possibly with more data one could appreciate the asymmetry already partially visible in these data when transitioning from negative-to-borderline with respect to the borderline-to-positive.

The integration of model and grading allows to compare semi-quantification values regardless of the approach (either SUVr-based or SUVr-independent) and employed tracer. This combination (a) defines transition regions and cut-off values; (b) indirectly confirms the appropriateness of a visual evaluation scale which is more apt to recognize transitions (similarly to several other clinical and visual scales (Scheltens et al., 1992)).

As models have only two free parameters, derived quantities (cut-off, transition region) are more robust with respect to the sample size and can be easily generalized.

The width of the transition region and the substantial similarity of the sigmoid models show that no tracer is the winner here, all are equivalently discriminating (i.e. no slope difference implies equivalent contrast). While to our knowledge there is no literature on tracers comparison within the same dataset and with the evaluation from the same set of readers, we can compare this result to Curtis et al. (Curtis et al., 2015), where the accuracy of all three fluorinated tracers in the phase-3 study is compared and similar conclusions are drawn. Importantly, the determination of a threshold for abnormality common across tracers is one of the required validation steps for the use of amyloid PET in AD following a recently proposed roadmap for biomarkers for an early diagnosis (Frisoni et al., 2017, Chiotis et al., 2017).

As a by-product of the work, we have studied the relationship between concordance and discordance of readers according to some indicators such as the degree of negativity / positivity, the quality of the scan and the binary evaluation.

On the reader concordance, first we notice a very good agreement among readers in binary lecture, accuracy ranging from 86% to 94%, meaning that in routine clinical practice only about one out of ten scans might be read with opposite conclusions. If on the one hand the present experimental setting does not fully reproduce the clinical reality where a doubtful scan is usually evaluated together by more than one reader and sometimes with the aid of semi-quantification tools (while here the raters were blind), on the other hand our raters were high to intermediate experts thus likely more skilled than the average of the real world. However, this figure is in keeping with other studies (Collij et al., 2019; Nayate et al., 2015) – if not higher – and points to the need of semi-quantification tools in assisting the nuclear medicine physician in the binary interpretation of scans.

In more details, when we look at the grading we see that while the overall observed ICC was very good, the discrepancies in the mild-negative / borderline regions (latitude) are rather significant. That is, despite the differences in expertise among readers and the multi-centre nature of the study, the learning curve for visual amyloid PET readings is not steep after a moderate degree of expertise has been acquired; on the other hand, evaluation errors are not evenly distributed across the positivity spectrum.

Considering the three tracers altogether we observed a ‘U’-shape distribution with higher percentage at the two extremes and progressively lower percentages toward the borderline cases (see Fig. 7 in supplementary materials). With individual tracers this pattern was less evident with flutemetamol disclosing a higher percentage in mild negative than in negative subjects while it was stronger with florbetaben. This mismatch could be due to the higher prevalence of subjects with AD and with non-AD conditions as compared to the flutemetamol cohort (Table 1).

As remark on the evaluations with and without the CT information, we first remind that readers have been trained to read amyloid PET scans as taken alone, leaving the use of CT/MRI only in doubtful cases, as per approved courses administered by pharmaceutical companies on the respective products; second, readers are all rather experienced; third, evaluation results with and without CT scans are not identical but simply statistically equivalent. This latter statement meaning that there were indeed patients whose evaluation was changed because of the CT information, but the cohort statistical distribution was not significantly altered.

We have to say we used data collected during clinical routine from sparse European centers and thus carrying inhomogeneity in scan quality and characteristics of patients. If this may have generated high variability among scans, it is however the reality collected in naturalistic cohorts and thus closer to the real world with respect to the setting of clinical trials.

Inhomogeneities are also evident when looking at latitude scans, where the apparent different relationship with the tracers can be ascribed to the diversity of cohort provenance and statistics.

Interestingly, however, we failed to find a correlation between scan quality and latitude (i.e., degree of differences among readers). This may mean that the intrinsic subjectivity in human eye when reading an amyloid PET scan is higher than quality inhomogeneity among scans. This represents a distinct source of disagreement among readers that adds to the one possibly deriving from low quality (Schmidt 2015).

Coming to the not-clearly positive/negative scans, we observed that almost half (i.e., 46%) of scans were visually rated either as borderline (10.8%) or mildly negative/positive (35.2%). Thus, the amount of transitional patients is considerable even in the clinical setting facing symptomatic patients and not only in the studies in the general population dealing with asymptomatic subjects. Apolipoprotein E epsilon-4 genotype is a major determinant of amyloid load but we miss this data in most patients so we cannot evaluate its influence on our population but it is likely other variables can act on amyloid deposition rate (Grimmer et al., 2014; Wang et al., 2017). Moreover, differences in disease severity course may also be reflected by differences in amyloid load among subjects with MCI (Villemagne and Rowe, 2013).

This work, moreover, is timely regarding its possible clinical applications. Firstly, it could be used to indirectly compare anti-amyloid compounds in clinical trials based on different tracers to evaluate drug-specific differences in target engagement and efficacy in brain amyloid clearance, thus allowing a better understanding of their mode of action. Moreover, if and when an anti-amyloid agent will be approved for clinical use, availability of an approach to directly compare PET fluorinated tracers will probably allow to streamline the eligibility criteria evaluation and thus the treatment access.

A further possible by-product of the availability of validated, tracer-independent cut-off and transition values that differentiate positive and negative scans is represented by their use during resident training to challenge the new readers with progressively difficult cases.

4.1. Study limitations

We have evaluated average tracer uptake in a volumetric ROI distributed in the whole brain without further analyzing regional differences. Some authors have reported that amyloid brain deposition in specific regions has higher predictive value toward transition to dementia or better correlate with cognitive impairment (Grothe et al., 2017; Cho et al., 2018). This exploration was beyond the aim of the present study although the resolution of this issue might have been relevant to rate especially borderline cases. We plan to further explore this issue in the future with a more homogeneous patient sample.

Another limitation is that we lacked coregistered CT in a number of cases (50%), as only PET scans were transferred and for the oldest ones recovery of CT was unfeasible. Indeed, it has been shown that reading amyloid PET with coregistered CT improves correct classification compared to PET scan alone (Curtis et al., 2015). However, we did not observe significant differences in classification intra- and inter-observer in the subset of patients (>50% of the whole sample) with CT available.

Finally, APOE information was available in <10% of all cases only. It is therefore omitted in the demographic table and it was not used in this study. However, we did not investigate the reason for positivity nor the interplay with demographic variables. The semi-quantification ranking, the visual grading and their relationship should therefore be independent from the APOE information.

Appendix A. Supplementary data

Supplementary material